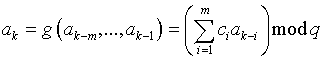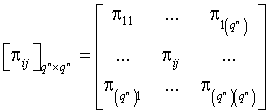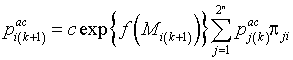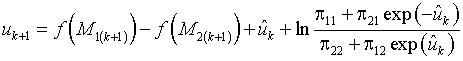УДК 621.391.266
МЕТОД ПОСЛЕДОВАТЕЛЬНОЙ ОЦЕНКИ СИГНАЛОВ НА ОСНОВЕ МОДЕЛИ МНОГОСВЯЗНОЙ ЦЕПИ МАРКОВА
Д. Е. Прозоров
Вятский государственный университет
Получена 16 октября 2013 г.
Аннотация. В статье рассмотрена задача последовательной оценки псевдослучайных сигналов (ПСС), построенных на рекуррентных последовательностях максимального периода (М-последовательностях). В качестве модели М-последовательности предложена многосвязная цепь Маркова. На основе предложенной модели разработан алгоритм нелинейной фильтрации ПСС, позволяющий сократить время кодовой синхронизации в системах связи с расширением спектра методом прямой последовательности.
Ключевые слова: кодовая синхронизация, многосвязная цепь Маркова, последовательная оценка, псевдослучайный сигнал.
Abstract: The problem of sequential estimation of pseudonoise (PN) signals derived from m-sequences is considered. The multilink Markov chain is proposed as a model of m-sequence. The algorithm of nonlinear filtering of PN signals is developed based on proposed model. This algorithm allows reducing the time of code synchronization in DSSS systems.
Key words: code synchronization, multilink Markov chain, sequential estimation, pseudonoise signal.
1. Введение
Линейные рекуррентные последовательности (ЛРП) широко используются для формирования псевдослучайных сигналов (ПСС) в коммуникационных и навигационных системах с расширением спектра методом прямой последовательности (DSSS – direct-sequence spread spectrum). Примерами таких систем являются DS-CDMA, GPS/Navstar, Glonass и беспроводные сети стандарта IEEE 802.11b. Для извлечения информации из принимаемого сигнала приемные устройства DSSS-систем должны проходить несколько этапов синхронизации: частотная и фазовая синхронизация, тактовая синхронизация и кодовая синхронизация.
Известно большое количество методов поиска и кодовой синхронизации ПСС [1] – [15]. Например, кодовая синхронизация ПСС может осуществляться с помощью многоканальных корреляторов или схем циклического поиска, в основе которых лежит пошаговая синхронизация искомого ШПС с его копией в приемнике [8]. В первом случае требуются большие технические ресурсы, а во втором – временные.
При относительно высоком отношении сигнал/шум методом, позволяющим снизить временные затраты на поиск и кодовую синхронизацию ПСС является метод последовательной оценки символов, предложенный Р. Уордом в работе [1]. Метод посимвольной оценки Уорда (RASE – Rapid Acquisition by Sequential Estimation) основан на рекуррентном свойстве ЛРП, которое позволяет по любому неискаженному сегменту ЛРП длиной m символов (m – размер регистра сдвига генератора ЛРП) синтезировать в приемном устройстве опорную ЛРП с требуемой задержкой. Однако, при снижении отношения сигнал/шум, вероятность правильной оценки символов ЛРП становится низкой и эффективность метода последовательной оценки символов быстро снижается [1].
Модификации метода Уорда, разработанные с целью компенсации указанного недостатка, описаны в работах [2] – [11]. В указанных работах предлагается формировать метки ненадежности символов [2], использовать дополнительные символы ЛРП для обнаружения и исправления ошибок [3] – [6], схемы с «мягким» принятием решений (RSSE – Recursive Soft Sequential Estimation) [9], или внутрипериодное накопление сигналов [7], [10], [11].
Еще одним методом, основанным на идее последовательной оценки символов ПСС, является метод приема с внутрипериодной нелинейной фильтрацией ПСС, использующий цепь Маркова в качестве модели последовательности символов ЛРП [12]. Модификации указанного метода рассмотрены в работах [13]-[15].
В статье разработан алгоритм нелинейной фильтрации ПСС, который является развитием алгоритмов, рассмотренных в [12] – [15]. В качестве модели ЛРП использована многосвязная цепь Маркова.
2. Марковская модель линейной рекуррентной последовательности
Линейной рекуррентной
последовательностью называется последовательность ![]() , определяемая
рекуррентным соотношением
, определяемая
рекуррентным соотношением
где ![]() – линейная функция,
– линейная функция, ![]() ,
, ![]() ,
,![]() .
.
ЛРП имеют период ![]() .
.
В системах связи обычно используют
ЛРП максимального периода с основанием ![]() (например,
М-последовательности).
(например,
М-последовательности).
Очевидно, что
комбинация из n символов ЛРП ![]() ,
, ![]() однозначно
зависит от комбинации
однозначно
зависит от комбинации ![]() из m символов ЛРП, что можно записать в виде
вероятностного соотношения
из m символов ЛРП, что можно записать в виде
вероятностного соотношения
Пусть ![]() ,
, ![]() . Из выражения (2) получим
. Из выражения (2) получим
Общее количество различающихся метасостояний
![]() равно
равно ![]() . Если
. Если ![]() , то
, то ![]() и
уравнение (3) преобразуется в
и
уравнение (3) преобразуется в
Пример 1.
Пусть ![]() и
и
Тогда
![]() = 1 1 1 0 0 1 0, 1 1 1 …
= 1 1 1 0 0 1 0, 1 1 1 …
Для ![]() :
: ![]() ,
, ![]() .
.
Тогда
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]() …
…
Для ![]() :
:
![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Тогда
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]() …
…
При ![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() и
и
![]() =
= ![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]() …
…
Метасостояние ![]() не
встречается.
не
встречается.
Рис. 1 иллюстрирует
последовательность метасостояний ![]() при
при ![]() .
.
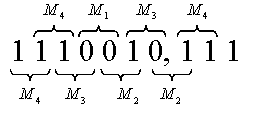
Рис. 1. Метасостояния ЛРП.
В момент наступления кодовой
синхронизации приемное устройство генерирует опорную последовательность, ![]() посимвольно совпадающую с ЛРП
посимвольно совпадающую с ЛРП ![]() принимаемого сигнала. Из уравнения (1)
следует, что сгенерировать такую ЛРП можно при наличии m последних неискаженных символов ЛРП
принимаемого сигнала.
принимаемого сигнала. Из уравнения (1)
следует, что сгенерировать такую ЛРП можно при наличии m последних неискаженных символов ЛРП
принимаемого сигнала.
Пусть ![]() –
оценка следующего,
–
оценка следующего, ![]() -го значения опорного ЛРП,
выполненная в k-м такте;
-го значения опорного ЛРП,
выполненная в k-м такте; ![]() ,
, ![]() . После
наступления кодовой синхронизации соблюдается условие
. После
наступления кодовой синхронизации соблюдается условие
Уравнение (6) означает, что оценка
метасостояния ЛРП, сформированная в k-м такте в приемном устройства совпадает с ![]() -м метасостоянием ЛРП принимаемого
сигнала.
-м метасостоянием ЛРП принимаемого
сигнала.
При наличии аддитивной смеси сигнала и шума на входе приемного устройства условные вероятности переходов (6) можно представить в виде матрицы
где ![]() .
.
Матрица (7) удовлетворяет следующим условиям
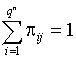 ,
, ![]() ,
, ![]() . (8)
. (8)
Подобные матрицы называются марковскими [17]. При этом последовательность переходов
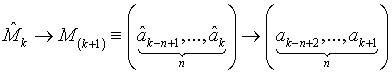 (9)
(9)
можно рассматривать как марковскую цепь со связностью n.
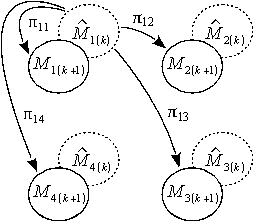
Рис. 2. Диаграмма переходов из метасостояния ![]() для
для ![]() .
.
Диаграмма возможных переходов из
метасостояния ![]() для цепи Маркова со связностью
для цепи Маркова со связностью ![]() представлена на рис.2 [18].
представлена на рис.2 [18].
3. Постановка задачи
Пусть на входе приемного устройства в
момент времени ![]() наблюдается аддитивная смесь ПСС
и шума
наблюдается аддитивная смесь ПСС
и шума
![]() , (10)
, (10)
где A
– амплитуда принимаемого сигнала, ![]() – несущая частота,
– несущая частота, ![]() , последовательность
, последовательность ![]() – ЛРП максимального периода
(М-последовательность) с периодом
– ЛРП максимального периода
(М-последовательность) с периодом ![]() ,
, ![]() – фаза сигнала,
– фаза сигнала, ![]() –
белый гауссовский шум,
–
белый гауссовский шум,
![]() ,
, 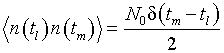 . (11)
. (11)
Необходимо разработать алгоритм фильтрации ПСС, построенного на М‑последовательности и структуру приемного устройства ПСС.
4. Апостериорная вероятность метасостояний ЛРП
Будем считать, что последовательность
метасостояний ![]() представляет собой сложную
регулярную цепь Маркова с
представляет собой сложную
регулярную цепь Маркова с ![]() состояниями,
состояниями, ![]() .
.
Пусть в приемном устройстве ПСС
формируется оценка ![]() метасостояния ЛРП принимаемого
сигнала (
метасостояния ЛРП принимаемого
сигнала (![]() ), где
), где ![]() –
оценка следующего,
–
оценка следующего, ![]() -го значения опорного ЛРП,
-го значения опорного ЛРП, ![]() – последовательность оценок символов
принимаемого ПСС.
– последовательность оценок символов
принимаемого ПСС.
Как показано в п.2 последовательность
переходов ![]() можно рассматривать как марковскую цепь
со связностью n и матрицей
вероятностей переходов (7).
можно рассматривать как марковскую цепь
со связностью n и матрицей
вероятностей переходов (7).
Апостериорная плотность вероятности
метасостояния ![]() [19,20] :
[19,20] :
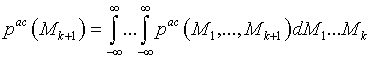 . (12)
. (12)
Многомерная апостериорная плотность
вероятности последовательности ![]() находится по формуле
обратной вероятности
находится по формуле
обратной вероятности
![]() , (13)
, (13)
![]() – функция правдоподобия,
– функция правдоподобия, ![]() – априорная многомерная плотность
вероятности последовательности
– априорная многомерная плотность
вероятности последовательности ![]() .
.
Так как шум ![]() является
некоррелированным, то функцию правдоподобия
является
некоррелированным, то функцию правдоподобия ![]() можно
преобразовать к виду
можно
преобразовать к виду
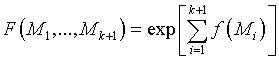 , (14)
, (14)
где ![]() .
.
Для цепи Маркова априорная плотность
вероятности ![]() может быть определена через произведение [19,
20]
может быть определена через произведение [19,
20]
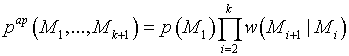 , (15)
, (15)
где ![]() – плотность вероятности
перехода от метасостояния
– плотность вероятности
перехода от метасостояния ![]() в i-м такте к метасостоянию
в i-м такте к метасостоянию ![]() в (i+1)-м такте.
в (i+1)-м такте.
Подставляя (13)-(15) в (12) получим
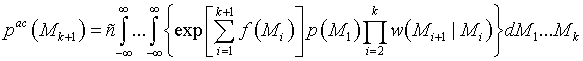 . (16)
. (16)
Поскольку
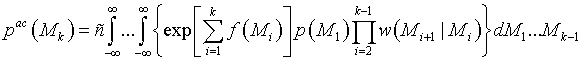 ,
,
то уравнение (16) можно преобразовать к рекуррентному виду, более удобному для вычислений [20]
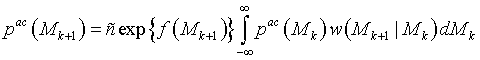 . (17)
. (17)
Плотность условной вероятности ![]() может быть представлена в форме [19]
может быть представлена в форме [19]
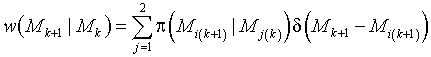 , (18)
, (18)
где ![]() означает i-е метасостояние ЛРП на
означает i-е метасостояние ЛРП на ![]() -м такте,
-м такте, ![]() –
дельта-функция Дирака,
–
дельта-функция Дирака, ![]() – элемент матрицы вероятностей
переходов (7).
– элемент матрицы вероятностей
переходов (7).
Запишем распределение апостериорных вероятностей
![]() в виде [19]
в виде [19]
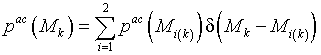 (19)
(19)
и, подставив (18), (19) в (17), получим
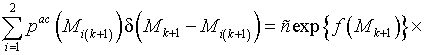 (20)
(20)
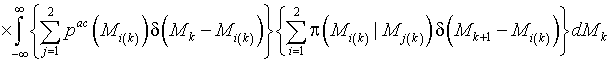 .
.
Используя фильтрующее свойство
дельта-функции, после интегрирования уравнения (20) получим систему из ![]() уравнений для апостериорных вероятностей
метасостояний
уравнений для апостериорных вероятностей
метасостояний ![]() [18]
[18]
где ![]() ,
, ![]() – логарифм функции правдоподобия
– логарифм функции правдоподобия ![]() ‑го метасостояния ЛРП в
‑го метасостояния ЛРП в ![]() -м такте.
-м такте.
5. Уравнения нелинейной фильтрации символов ПСС для модели односвязной цепи Маркова
Пусть ![]() , тогда
, тогда
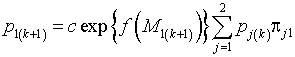 , (22)
, (22)
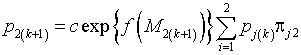 . (23)
. (23)
Разделим уравнение (22) на уравнение (23) и прологарифмируем результат
где
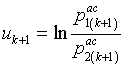 ;
;
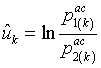 .
.
Знак «^» подчеркивает тот факт, что
величина ![]() является оценкой, формируемой в приемном
устройстве в k-м такте.
является оценкой, формируемой в приемном
устройстве в k-м такте.
Уравнение (24) является частным случаем и совпадает с уравнениями, полученными в работах [12] – [13].
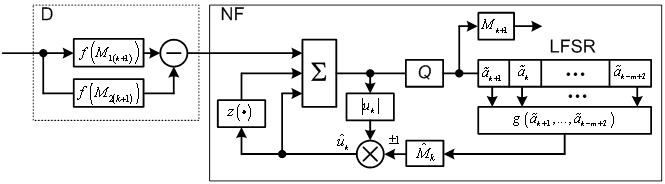
На рис.3 представлена структура
приемного устройства ПСС для модели односвязной цепи Маркова, реализующая
уравнение (24). Приемное устройство содержит: дискриминатор (D), вычисляющий разность функций
правдоподобия ![]() , бинарный квантователь (Q) с нулевым порогом, линейный регистр
сдвига с обратными связями (LFSR),
формирующий оценки
, бинарный квантователь (Q) с нулевым порогом, линейный регистр
сдвига с обратными связями (LFSR),
формирующий оценки ![]() , схему формирования оценок
, схему формирования оценок ![]() и нелинейный фильтр (NF), содержащий сумматор
( ∑ ) и схему вычисления нелинейной функции
и нелинейный фильтр (NF), содержащий сумматор
( ∑ ) и схему вычисления нелинейной функции
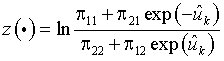 .
.
Рис.3. Структура приемного устройства ПСС для модели односвязной цепи Маркова.
В работе [16] показано, что алгоритм
нелинейной фильтрации (24) позволяет сократить время кодовой синхронизации в 1.5
и более раз при отношениях сигнал/шум ![]() дБ по
сравнению с методом Уорда [1].
дБ по
сравнению с методом Уорда [1].
6. Уравнения нелинейной фильтрации символов ПСС для модели многосвязной цепи Маркова
Рассмотрим в качестве примера уравнения
нелинейной фильтрации ПСС для модели цепи Маркова со связностью ![]() .
.
Пронормируем уравнения (21) на ![]() , где
, где ![]() –
логарифм функции правдоподобия выборки белого гауссовского шума и
прологарифмируем результат
–
логарифм функции правдоподобия выборки белого гауссовского шума и
прологарифмируем результат
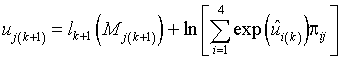 ,
,
![]() . (25)
. (25)
В уравнении (25)
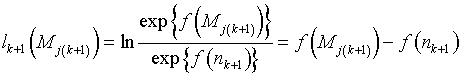 –
–
– логарифм отношения правдоподобия для метасостояния ![]() ,
, ![]() ,
, ![]() – оценка, формируемая в приемном
устройстве.
– оценка, формируемая в приемном
устройстве.
Распознавание метасостояний ![]() осуществляется в соответствии с критерием
максимума апостериорной вероятности
осуществляется в соответствии с критерием
максимума апостериорной вероятности
![]() . (26)
. (26)
Пример 2.
Пусть ЛРП принимаемого сигнала
формируется по правилу (5) и метасостояния ЛРП определены аналогично примеру 1
(![]() ).
).
Учитывая, что
![]()
![]() , (27)
, (27)
где ![]() ,
, ![]() ,
, ![]() –
логарифм отношения правдоподобия r-го состояния
–
логарифм отношения правдоподобия r-го состояния ![]() ЛРП в k‑м такте, получим
ЛРП в k‑м такте, получим
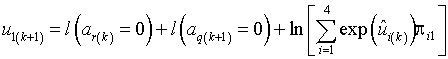 ,
,
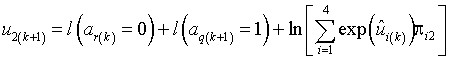 , (28)
, (28)
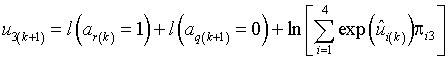 ,
,
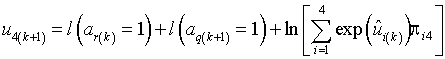 .
.
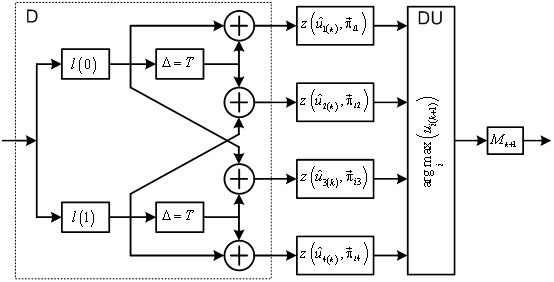
Приемное устройство, соответствующее уравнениям (28) и критерию (26) представлено на рис.4. Здесь «D» дискриминатор приемного устройства, «DU» – решающее устройство.
Рис.4. Структура приемного устройства ПСС
для модели цепи Маркова со связностью
![]() .
.
На рис.4 вектором ![]() обозначена i-я строка матрицы вероятностей переходов (7), функция
обозначена i-я строка матрицы вероятностей переходов (7), функция ![]() выполняет преобразование
выполняет преобразование
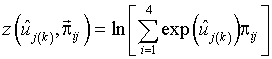 . (29)
. (29)
Последовательность ![]() символов ЛРП можно найти используя
соотношение
символов ЛРП можно найти используя
соотношение ![]() .
.
6. Эксперимент
Наибольший интерес представляет
кодовая синхронизация ПСС, сформированных на ЛРП, с периодом большим ![]() символов. ЛРП с такими периодами наиболее
часто применяются в современных системах связи.
символов. ЛРП с такими периодами наиболее
часто применяются в современных системах связи.
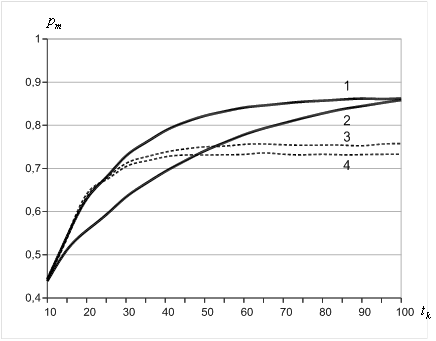
Рис.5. Вероятность правильного распознавания m-символьных кодовых комбинаций ПСС. Графиками обозначены варианты:
1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
, ![]() ; 3)
; 3) ![]() ,
, ![]() ; 4)
; 4) ![]() ,
, ![]() .
.
На рис. 5 представлен график вероятности
правильного распознавания ![]() кодовых комбинаций из
кодовых комбинаций из ![]() символов ЛРП. График получен имитационным
моделированием приемных устройств (рис. 3) и (рис. 4) при отношении
сигнал/шум равном 0 дБ.
символов ЛРП. График получен имитационным
моделированием приемных устройств (рис. 3) и (рис. 4) при отношении
сигнал/шум равном 0 дБ.
ЛРП сформирована по правилу
![]() . (30)
. (30)
Период ЛРП: ![]() .
.
Сплошными кривыми обозначены графики для приемного устройства (рис.4); пунктирными кривыми – для приемного устройства (рис.3).
7. Заключение
Разработчикам радиоприемных устройств систем связи с расширением спектра методом прямой последовательности (DSSS – direct-sequence spread spectrum) часто приходится искать компромисс между сложностью приемных устройств и временем кодовой синхронизации псевдослучайных сигналов. Наименьшее время поиска и кодовой синхронизации обеспечивают многоканальные схемы на основе корреляторов [8]. Значительно меньшей структурной сложностью обладают схемы последовательной оценки, однако их эффективность падает при уменьшении отношения сигнал/шум [1].
Предложенная модель ЛРП позволяет
синтезировать структуры приемных устройств ПСС произвольной сложности, в
зависимости от требований, предъявляемых к помехоустойчивости приемного
устройства. Так, использование в качестве модели ЛРП цепи Маркова со связностью
![]() позволяет повысить вероятность
правильного распознавания кодовых m-символьных комбинаций ПСС (где m – размер регистра сдвига генератора ЛРП) на 13%-18%
по отношению к методу, основанному на модели односвязной (простой) цепи Маркова.
позволяет повысить вероятность
правильного распознавания кодовых m-символьных комбинаций ПСС (где m – размер регистра сдвига генератора ЛРП) на 13%-18%
по отношению к методу, основанному на модели односвязной (простой) цепи Маркова.
Литература
1. R. Ward. Acquisition of Pseudonoise Signals by Sequential Estimation // IEEE Transactions on Communications, vol. 13, no. 4, pp. 475–483, Dec. 1965.
2. Тепляков И.М., Рощин Б.В., Фомин А.И., Вейцель В.А. Радиосистемы передачи информации. – М.: Радио и связь, 1982. – 264 с.
3. Григорьев А.А. Некоторые мажоритарные алгоритмы определения фазы псевдослучайных последовательностей. – Изв. вузов СССР. Радиоэлектроника, 1979. Т.22, №4, с.33-41.
4. Журавлев В. И., Леонтьев М. А. О статистических показателях системы поиска псевдослучайных сигналов с мажоритарной оценкой символов. – VII Всесоюз. конф. по теории кодирования и передаче информации: Тез. докл. – Москва – Вильнюс, 1978.
5. Kilgus C. C. Pseudonoise code acquisition using majority logic decoding // IEEE Trans., 1973, v. COM-21, №1.
6. Лосев В.В., Номоконов В.Н. Синхронизация М-последовательностей модифицированными методами последовательной оценки // Радиотехника и электроника, 1977, 22, №3.
7. Чердынцев В.А. Проектирование радиотехнических систем со сложными сигналами. – Минск: Вышейшая школа, 1979. – 192 с.
8. Журавлев В.И. Поиск и синхронизация в широкополосных системах. – М.: Радио и связь, 1986. – 240 с.
9. Lie-Liang Yang and L. Hanzo. Acquisition of m-sequences using recursive soft sequential estimation // Wireless Communications and Networking, 2003. Vol. 1, pp. 683–687.
10. S. Yoon, I. Song, and S. Yong Kim. Seed accumulating sequential estimation for PN sequence acquisition at low signal-to-noise ratio // Signal Processing, vol. 82, №11, pp. 1795–1799, Nov. 2002.
11. J. Wang, X. Hu, Y. Zhang, and Q. Dai. A Rapid Code Acquisition Scheme for DS/SS Systems // Wireless Personal Communications, vol. 39, no. 4, pp. 503–514, Jun. 2006.
12. E. P. Petrov and D. E. Prozorov. Synthesis of Devices for the Fast Search for Noiselike Signals that are Based on Multidigit Recurrent Sequences of the Maximum Period // Journal of Communications Technology and Electronics, vol. 50, no. 10, pp. 1186–1191, Oct. 2005.
13. Петров Е.П., Прозоров Д.Е., Петров И.Е., Смирнов А.В. Быстрый поиск шумоподобных сигналов // Успехи современной радиоэлектроники. Зарубежная радиоэлектроника, 2008, № 8, с. 47-69.
14. Прозоров Д.Е., Чащин А.А. Нелинейная фильтрация многоуровневых шумоподобных сигналов в системах связи с повышенной конфиденциальностью // Цифровая обработка сигналов, 2007, № 2, с. 9-13.
15. Прозоров Д.Е. Адаптивная нелинейная фильтрация многоуровневых шумоподобных сигналов // Системы управления и информационные технологии, 2007, №3.1(29), с. 190-194.
16. Прозоров Д.Е., Смирнов А.В. Анализ времени кодовой синхронизации шумоподобных сигналов // T-Comm: Телекоммуникации и транспорт, 2011, №6, с. 50-51.
17. R. Bellman, Introduction to matrix analysis, 2nd ed. Philadelphia: Society for Industrial and Applied Mathematics, 1997.
18. Prozorov D., Chistyakov A. Nonlinear Filtering of Pseudonoise Signals Using High-Order Markov Chain Model // Proceedings of IEEE East-West Design & Test Symposium (EWDTS’2013), Rostov-on-Don, Russia, September 27 – 30, 2013, pp. 328-332.
19. Амиантов И.Н. Избранные вопросы статистической теории связи. – М.: Сов. радио, 1971. – 416 с.
20. Стратонович Р.Л. Применение теории процессов Маркова для оптимальной фильтрации сигналов // Радиотехника и электроника, 1960. - Т.11. – С. 1751 – 1763.