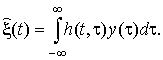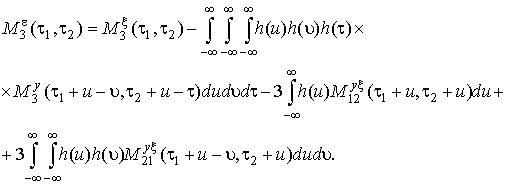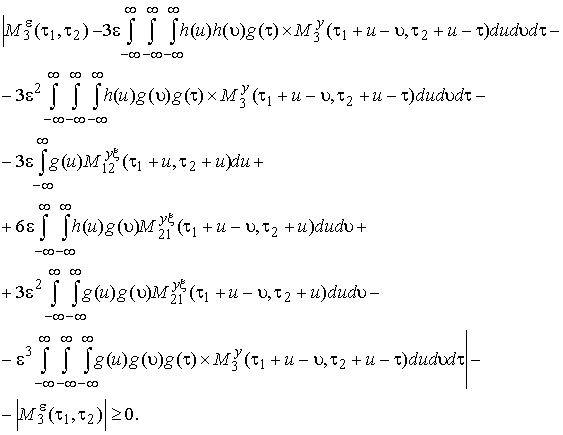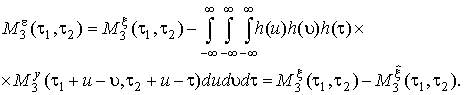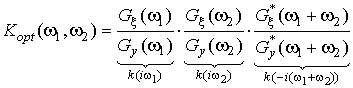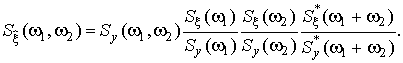УДК 681.513.6
О разработке оптимального фильтра выделения полезного сигнала в биспектральной области по критерию минимума абсолютной ошибки третьей степени
А. Е. Манохин, А. А. Зародов
Институт радиоэлектроники и информационных технологий-РТФ УрФУ им. первого Президента РФ Б.Н.Ельцина, кафедра радиоэлектронных и телекоммуникационных систем, Екатеринбург
Статья поступила в редакцию 4 августа 216 г., после доработки – 22 сентбря 2016 г.
Аннотация. В работе решается задача синтеза оптимального фильтра выделения полезного сигнала в биспектральной области по критерию минимума абсолютной ошибки 3 степени. Основным преимуществом фильтра является его способность теоретически идеально выделить биспектр полезного сигнала. В то же время оптимальный фильтр Винера в биспектральной области выделяет биспектр сигнала без ошибки, если он не перекрывается с биспектром помехи. В этом случае после оптимальной фильтрации по критерию минимума абсолютной ошибки 3 степени при восстановлении полезного сигнала из биспектра среднеквадратическая ошибка значительно ниже, чем при применении винеровской фильтрации.
Ключевые слова: биспектр, моментная функция 3 порядка, фильтр Винера.
Abstract. The problem of synthesizing an optimal filter of a useful signal in a bispectral domain by the least mean absolute third error criteria is solved in the work. Core advantage of the filter is its capability to select the useful signal bispectrum theoretically ideally. At the same time the Wiener's optimum filter selects the desired signal bispectrum without an error in bispectral domain if a signal and disturbance bispectrums are not spanned. In this case the least mean square error is considerably lower after an optimal filtration by the least mean absolute third error criteria using recovering a desired signal from the bispectrum, than using Wiener’s filtration.
Key words: bispectrum, third moment function, Wiener’s filter.
Введение
Биспектральное преобразование позволяет подавлять помехи с симметричными распределениями и нулевыми математическими ожиданиями. Спектр 3 порядка или биспектр наблюдаемого процесса y определяется как двойное преобразование Фурье моментной (кумулянтной) функции 3 порядка.
Рассмотрим основные свойства биспектра [1]:
1) Имеет комплексный характер и состоит из произведения амплитудного и фазового биспектров:
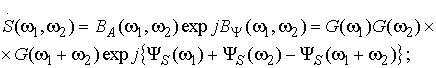(1)
где 
— амплитудный биспектр, 
— фазовый биспектр; G(ω)
— амплитудный спектр, Ψ(ω) — фазовый спектр.
2) Периодичен с периодом 2p
. (2)
3) Симметричен
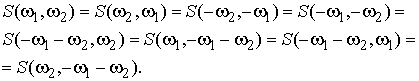(3)
4) Инвариантен к сдвигу D сигнала:
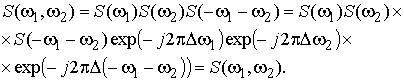(4)
Из свойства симметрии вытекает, что знание биспектра в треугольной области w³0, w1³w2, w1+w2£p, достаточно для полного описания биспектра [1].
Все методы биспектрального оценивания делятся на прямые и косвенные. Прямые методы основаны на получении оценок спектра сигнала посредством прямого преобразования Фурье, а затем использования этих оценок для получения биспектра. Косвенные методы предполагают сначала вычисление моментной (кумулянтной) функции 3 порядка, а затем с помощью двумерного преобразования Фурье и использования двумерной функции окна формирование оценки биспектра.
В общем случае оценки биспектра по спектральным и моментным функциям оказываются различными, однако при больших выборках и большом числе сегментов как прямые, так и косвенные методы оценивания дают приближенно несмещенные и состоятельные оценки [1]. Вместе с тем, прямой метод оценивания биспектра более применим на практике из-за более высокого быстродействия за счет применения БПФ.
Рассмотрим прямой метод. Пусть имеется набор данных y(1), y(2),…,y(N) для биспектрального оценивания. Представим биспектральное преобразование в 4 этапа:
1) Разделение данных на K сегментов по M отсчетов и вычитание из каждого сегмента среднее значение.
2) Прямое преобразование Фурье каждого k-го сегмента 
3) Формирование k-й оценки биспектра на частотах w1, w2, w1+w2:
, (5)
где * — операция комплексного сопряжения;
4) Расчет усредненной оценки биспектра по k сегментам:
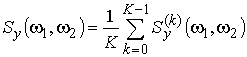, (6)
где K — количество усреднений биспектров.
Методов восстановления сигнала из оценки биспектра существует большое множество, некоторые из них изложены в [2–5]. Для указанных методов характерен ряд достоинств, а также ограничений и недостатков, которые требуют в каждом конкретном случае (при обработке сигналов) отдельных исследований и компьютерного моделирования.
Если моментная функция 3 порядка помехи отлична от нуля, то биспектральным преобразованием подавить ее невозможно и необходимо искать другие методы фильтрации полезного сигнала.
Традиционными являются методы с использованием линейного фильтра. Если решается задача фильтрации случайного процесса ξ(t), взаимодействующего аддитивно с помехой n(t), с нулевыми средними, то оценка полезного сигнала во временной области на выходе фильтра с импульсной характеристикой h(t):
где y(t) = ξ(t)+ n(t).
Фильтрация по критерию минимума среднего квадрата ошибки (критерий LMS[1]) оценки приводит к синтезу фильтра в частотной области (при независимости сигнала и помехи) с коэффициентом передачи по Винеру, равным отношению спектральной плотности мощности сигнала к спектральной плотности мощности аддитивной смеси на входе фильтра.
Если фильтрация производится в биспектральной области, то оценка комплексного биспектра сигнала на выходе фильтра может быть представлена [1]:
, (8)
где k(w) — коэффициент передачи линейного фильтра на частоте w;
— биспектр входного сигнала.
Подставляя в формулу (8) оптимальный коэффициент передачи по Винеру и представив биспектр входного сигнала произведением спектров на частотах w1, w2 и w1+w2, получаем следующее выражение для биспектра выходного сигнала:
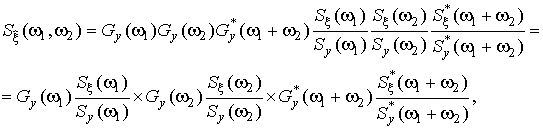(9)
где 
— спектр входного сигнала
линейного фильтра;
— спектральная плотность
мощности полезного сигнала;
— спектральная плотность мощности
входного сигнала.
Очевидно, что множители в произведении (9) есть спектры сигнала на выходе линейного винеровского фильтра, поэтому его использование в биспектральной области не дает никакого выигрыша в фильтрации при идеальном восстановлении сигнала по биспектру.
Вместе с тем, биспектр есть двойное Фурье-преобразование моментной функции 3 порядка, в связи с чем для наилучшего воспроизведения биспектра при фильтрации необходимо выбрать критерий минимизации абсолютной ошибки 3 степени.
Постановка задачи
Необходимо синтезировать комплексный коэффициент передачи линейного фильтра в биспектральной области, наилучшим образом выделяющего полезный сигнал, действующий на фоне аддитивной помехи. Для этого определим импульсную характеристику линейного фильтра, для которого минимизируется абсолютная ошибка третьей степени (критерий LMAT[2]). Центральная моментная функция 3 порядка ошибки выражается:
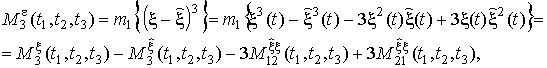(10)
где m1 — математическое
ожидание; 
и 
— смешанные
моментные функции 3 порядка.
Найдем каждое слагаемое в отдельности (кроме первого), подставив (7) в (10).
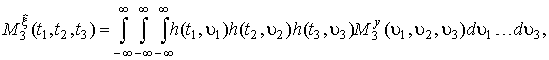(11)
где 
В случае, если процесс стационарен (по крайней мере, в широком смысле), а система имеет постоянные параметры, то, проводя замены u=t1–υ1, υ=t2–υ2, τ=t3–υ3 и вычитая во всех моментных функциях первый аргумент из остальных, находим второе слагаемое (первый аргумент у моментов опускается):
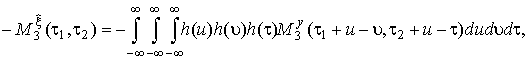(12)
где t1 = t2 – t1; t2 = t3 – t1.
Аналогично для третьего слагаемого с учетом замен и вычитания аргументов:
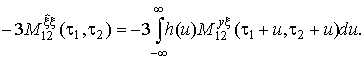(13)
Четвертое слагаемое:
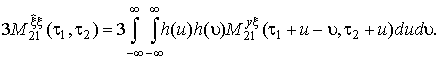(14)
Подставляя (12)–(14) в (10) получаем выражение для моментной функции ошибки 3 порядка:
Найдем теперь необходимое условие, которому должна удовлетворять h(τ) для того, чтобы абсолютная ошибка 3 степени была минимальной. Используем методику в [6], согласно которой введем g(τ) – весовую функцию некоторого произвольно осуществимого фильтра. Тогда h(τ)+εg(τ) есть весовая функция фильтра, и если h(τ) обеспечивает наименьшую абсолютную ошибку третьей степени, то выражение в правой части (15) по модулю при замене h(τ) на h(τ)+εg(τ) должно быть, по крайней мере, не меньше, чем до такой замены. Это должно быть верным при любом вещественном ε и для любой из относящихся к указанному классу функций g(τ).
(16)
При замене h(τ) на h(τ)+εg(τ) в (15) и с учетом (16) получаем следующее выражение:
Рассмотрим условия, при которых только последнее слагаемое при степени ε3 определяло бы изменения значения первого модуля в (17).
Приравняем к нулю члены при одинаковых степенях ε и ε2 и найдем корни интегральных уравнений:
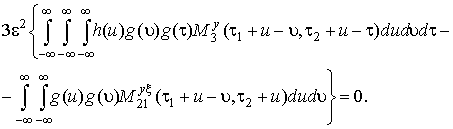(18)
Уравнение (18) выполняется при любой g(τ), только если
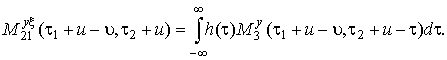(19)
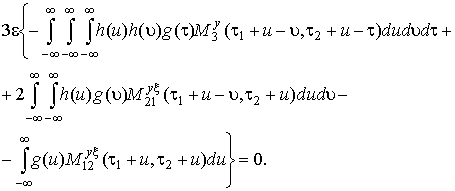(20)
Представим выражение в фигурных скобках формулы (20) в более удобном виде:
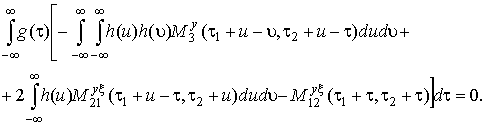(21)
Подставим выражение (19) в (21) и получим, что уравнение (21) выполняется при любой g(τ), только если
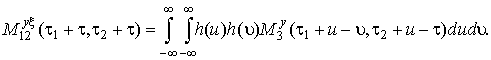(22)
Выполнение соотношения (22) для h(τ) есть необходимое условие для того, чтобы весовая функция обеспечивала минимум абсолютной ошибки третьей степени в классе линейных фильтров.
Достаточным условием будет являться
равенство нулю абсолютной ошибки третьей степени 
в
выражении (17). Тогда при любых значениях ε
и при любой g(τ) будет выполняться неравенство (16) и абсолютная ошибка
третьей степени всегда будет не меньше, чем при оптимальной h(τ).
Подставляя уравнения (19) и (22) в выражение (15), получаем центральную моментную функцию ошибки 3 порядка, которая равна разности моментных функций 3 порядка сигнала и его оценки:
Синтез коэффициента передачи оптимального фильтра в биспектральной области
Затем из (22) найдем АЧХ фильтра. Для того, чтобы исключить переменную t выполним свертку обоих частей выражения (22). В левой части получается моментная функция 3 порядка полезного сигнала, в правой — тройная свертка моментной функции 3 порядка входного сигнала фильтра с импульсной характеристикой h(τ):
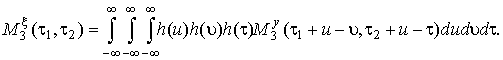(24)
Выражение (24) будет являться также достаточным условием
оптимальности h(τ). Проведем двойное преобразование Фурье моментной функции 
[7]:
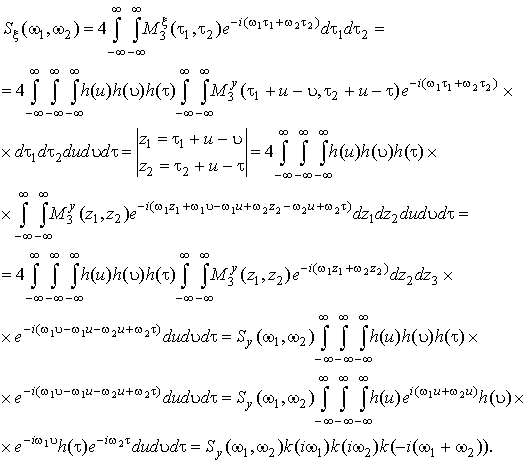(25)
Коэффициент передачи оптимального (нереализуемого) линейного фильтра по критерию минимума ошибки 3 степени выражается:
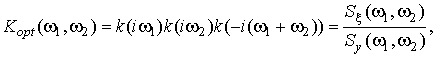(26)
где 
и 
—
биспектры полезного и входного сигналов соответственно.
При независимости сигнала и помехи (26) можно преобразовать:
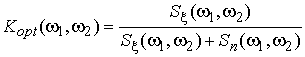, (27)
где 
— биспектр помехи.
Если биспектры в числителе и знаменателе выразить через произведение спектров, то:
где 
и — спектры
сигнала и смеси сигнала с помехой соответственно.
Минимальную абсолютную ошибку 3 степени найдем из (23), обнулив аргументы и представив ее как двойной интеграл разности двойных моментных спектров сигнала и его оценки:
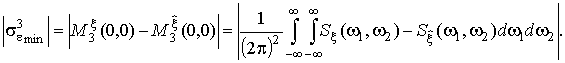(29)
С учетом (8) биспектр выходного сигнала можно записать:
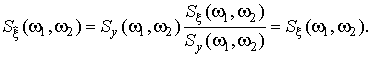(30)
Таким образом, биспектр входного сигнала фильтра сначала обеляется, а затем осуществляется оптимальная обработка белого шума для получения оценки биспектра полезного сигнала с минимальной абсолютной ошибкой 3 степени.
Подставляя ф. (30) в (29), находим, что минимальная абсолютная ошибка третьей степени всегда равна нулю (выполнение достаточного условия):
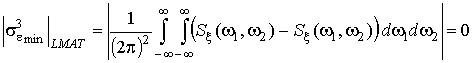. (31)
Если фильтрация производится оптимальным фильтром Винера (ФВ), то биспектр выходного сигнала равен:
Факторизовав спектральные плотности в произведение комплексно-сопряженных спектров процессов, формула (32) преобразуется:
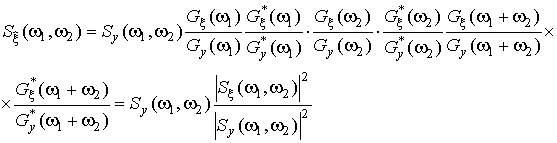(33)
Тогда абсолютная ошибка третьей степени всегда равна:
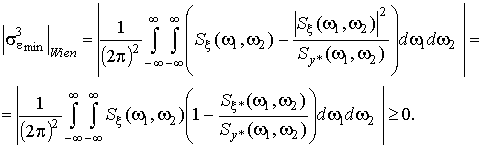(34)
Анализируя формулы (31) и (34), можно сделать вывод, что наилучшее воспроизведение биспектра, а равно и восстановление сигнала из биспектра производится при использовании оптимального коэффициента передачи в биспектральной области (28). В то же время, при использовании оптимального коэффициента передачи фильтра Винера минимальная ошибка 3 степени обращается в нуль только тогда, когда биспектры сигнала и помехи не перекрываются. В остальных случаях ошибка отлична от нуля.
Проведем компьютерное моделирование
процесса выделения импульсного сигнала (М-последовательность с порождающим
полиномом 
, которая имеет вид:
0000100101100111110001101110101) на фоне несимметричного телеграфного процесса
и гауссова шума согласно блок-схеме, изображенной на рис. 1.
В качестве оптимального используем фильтры в биспектральной области,
оптимальные по критериям LMAT (28) и LMS
(32).
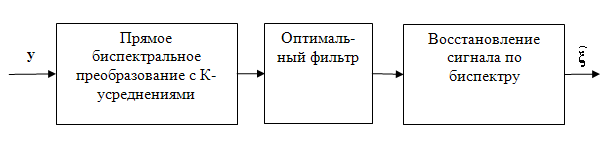
Рис. 1. Структурная схема оптимальной биспектральной обработки
Задается отношение мощности гауссовой помехи и импульсной помехи 0 дБ, а также отношение мощности сигнал-помеха на входе фильтра:
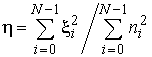(35)
Интенсивность[3] несимметричной телеграфной помехи — λТ=0.5. Длина выборки сигнала, подвергаемого прямому преобразованию Фурье, составляет N=512, минимальная длительность символа импульсного полезного сигнала — 8 отсчетов.
Для чистоты эксперимента предполагаем, что при восстановлении полезного сигнала из биспектра его фазо-частотная характеристика известна. В противном случае ошибка восстановления фазы повлияет на результаты моделирования.
В качестве критерия эффективности фильтрации используем нормированную к значению момента 3 порядка полезного сигнала абсолютную минимальную ошибку 3 степени:
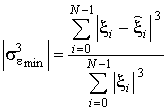. (36)
и нормированную к мощности полезного сигнала дисперсию ошибки воспроизведения сигнала:
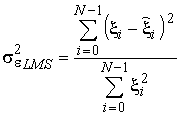(37)
Результаты моделирования отображены в таблицах 1, 2 и на рис. 2.
Таблица 1. Зависимость минимальной абсолютной ошибки 3 степени и дисперсии ошибки воспроизведения сигнала от количества усреднений биспектров (K[4]) при отношении мощности сигнал-помеха (η) на входе 0 дБ
|
К |
100 |
200 |
500 |
1000 |
5000 |
|
|
–34.4 |
–39.2 |
–42.1 |
–45.0 |
–52.9 |
|
|
–21.6 |
–25.6 |
–27.5 |
–29.3 |
–34.6 |
|
|
–19.6 |
–19.3 |
–19.2 |
–19.0 |
–19.0 |
|
|
–13.1 |
–13.0 |
–12.9 |
–12.9 |
–12.8 |
Таблица 2. Зависимость минимальной абсолютной ошибки 3 степени и дисперсии ошибки воспроизведения сигнала от отношения мощности сигнал-помеха (η) на входе при К=200
|
η, дБ |
–20 |
–15 |
–10 |
–5 |
0 |
5 |
10 |
15 |
20 |
|
|
–9.4 |
–13.7 |
–17.1 |
–21.3 |
–25.6 |
–28.3 |
–33.4 |
–38.9 |
–43.8 |
|
|
–2.9 |
–3.6 |
–5.1 |
–8.0 |
–13.0 |
–15.7 |
–17.1 |
–20.3 |
–24.7 |
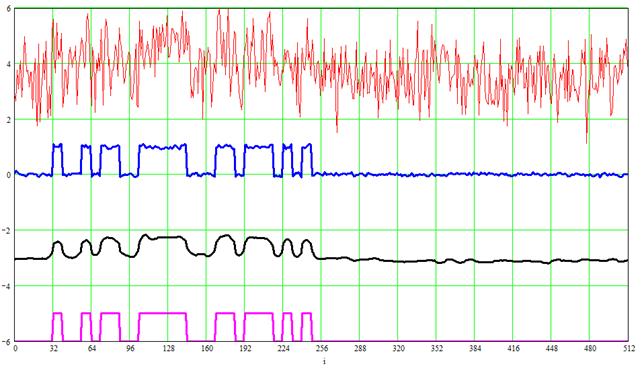
Рис. 2. Эпюры зашумленного полезного сигнала[5] на входе (красный) и выходе устройства биспектральной обработки при использовании оптимального фильтра по критерию LMAT (синий) и критерию LMS (черный), чистого полезного сигнала (розовый) при К=200, η = –5дБ (для наглядности эпюры сдвинуты по оси ординат относительно друг друга)
Выводы
1. Оптимальная фильтрация в биспектральной области по критерию минимальной абсолютной ошибки 3 степени имеет значительное преимущество перед оптимальным винеровским фильтром в воспроизведении полезного сигнала более чем на 20 дБ (при К³5000).
2. Минимальная абсолютная ошибка 3 степени достигает нуля при стремлении количества усреднений биспектров (параметра К) к бесконечности. Это объясняется обратно пропорциональной зависимостью дисперсии оценки биспектра и параметра К [1].
3. Оптимальный фильтр в биспектральной области по критерию минимальной абсолютной ошибки 3 степени может быть использован (при достаточной производительности устройств) в связных системах, где имеется возможность предварительной оценки полезных (пилотных) сигналов.
Литература
1. Никиас Х.Л., Рагувер М.Р. Биспектральное оценивание применительно к цифровой обработке сигналов. // ТИИЭР, 1987, Т.75, №7, c. 5–30.
2. Barlet H., Lohmann A.W. and Wirnitzer B. Phase and amplitude recovery from bispectra // Applied Optics. – September 1984. – Vol. 23. – pp.3121–3129.
3. Sundaramoorthy G., Raghuveer M.R. and Dianat S.A. Bispectral reconstruction of signal in noise: Amplitude reconstruction issues // IEEE Trans. Acoustic, Speech, and Signal Processing. – July 1990. – Vol.38, №7. – pp.1297–1306.
4. Мацуока Т., Ульрих Т.Дж. Оценивание фазового спектра сигнала по биспектру сейсмической записи // ТИИЭР. – Октябрь 1984.– Т.72, №10.– c.200–209.
5. Marron J.C., Sanchez P.P. and Sullivan R.C Unwrapping algorithm for least-square phase recovery from modulo 2 bispectrum phase // Journal of the optical society of America. – January 1990. – Vol.7, №1. pp.14–20.
6. Давенпорт В.Б., Рут В.Л.. Введение в теорию случайных сигналов и шумов. Перевод с английского Б.Г. Белкина; под ред. Р.Л.Добрушина. — М : Издательство иностранной литературы, 1960. — 468с.
7. Левин Б.Р. Теоретические основы статистической радиотехники. Книга первая. — М : Изд-во «Советское радио», 1969. 752 с.
[1] Least mean square (англ.).
[2] Least mean absolute third (англ.).
[3] Под интенсивностью понимается частота смены уровней несимметричного телеграфного процесса в интервале от нуля до максимальной амплитуды. Моменты скачков уровней подчиняются закону Пуассона.
[4] См. формулу (6).
[5] М-последовательность — 0000100101100111110001101110101.