ИМИТАЦИОННАЯ МОДЕЛЬ ЛОКАЦИОННОГО МЕТОДА ДИАГНОСТИКИ ЭЛЕКТРОЛИНИЙ С ДРЕВОВИДНОЙ ТОПОЛОГИЕЙ
Р. И. Шагиев
Казанский (Приволжский) Федеральный Университет
Статья поступила в редакцию 17 октября 2016 г.
Аннотация. В работе приведено описание имитационной модели локационного метода диагностики электролиний, позволяющей осуществлять оценку эффективности и точности определения места повреждений электролиний с произвольной древовидной топологией. Модель разработана в пакетах PSCAD/EMTDC и MATLAB и основана на фазовой частотно-зависимой модели электролинии. Модель прошла верификацию путем сравнения модельных данных с экспериментальными. Результаты исследования локационного метода для диагностики разветвленных линий продемонстрировали возможность обнаружения и определения расстояния до следующих видов повреждений: короткие замыкания на землю, межфазные замыкания, обрывы проводов.
Ключевые слова: локационный метод, рефлектометр, локатор, разветвленные электролинии, диагностика повреждений ЛЭП.
Abstract. The article describes a simulation model of time domain reflectometry (TDR) method for branched power line diagnostics. Developed model consists of two maim modules: generation module and processing module. Generation module is created in PSCAD/EMTDC environment and is based on phase frequency-dependent power line model. Generation module produces reflection traces for lines with arbitrary topology and allows simulating main types of faults: short circuit to ground, interphase circuit and wire breakage. The model takes into account the characteristics of the wire, the characteristics of the environment, the geometry and structure of the power lines. Processing module is created in MATLAB environment and designed for mathematical processing of the received signals. The simulation ends with the calculated distance to the line fault place. The results of the TDR method simulation demonstrated the ability to detect the main types of power lines faults with an error of no more than 0.07% (at high SNR). Attenuation of the reflected signal ranges from 10 dB to 20 dB depending on fault type.
Keywords: time domain reflectometry, TDR, reflectometer, locator, branched power lines, power lines diagnostics.
Введение
Оперативная диагностика электросетей позволяет регистрировать аварии на ранней стадии развития, предупреждать возникновение крупных аварийных ситуаций, а также максимально сокращать время простоя электролиний.
Локационный метод является дистанционным методом диагностики, основанном на распространении зондирующего сигнала вдоль линии и его отражении от мест неоднородности [1, 2]. Анализ литературы показал, что данный метод недостаточно изучен в следующих аспектах:
1) применение на линиях с разветвленной структурой при низких отношениях сигнал/шум;
2) эффективность локационного метода в зависимости от вида повреждения;
3) обоснование выбора типа и параметров зондирующего сигнала.
Указанные факторы обусловлены сложностью и трудоемкостью экспериментального исследования локационного метода диагностики, для осуществления которого необходимо создание макетов диагностирующего устройства и электролинии, либо вывод из работы действующей электролинии. Более того, экспериментальные исследования дают только ограниченный объем информации об исследуемом предмете из-за практической невозможности проведения всесторонних испытаний. Перечисленные проблемы, возникающие при экспериментальных исследованиях, преодолеваются путем имитационного моделирования.
В работе приведена имитационная модель локационного метода, позволяющей моделировать указанный метод диагностики для электролиний с произвольной конфигурацией, с применением трех видов зондирующих сигналов при различных отношениях сигнал/шум.
Модель электролинии
Основная трудность при моделировании воздушных электролиний и подземных кабелей заключается в том, что распространение радиоволн по ним имеет сильно нелинейный характер. Точное описание электролиний играет важную роль в моделировании электромагнитных переходных процессов в таких системах в целом.
В данной работе модель электролинии с разветвленной структурой создана на базе фазовой частотно-зависимой модели [3, 4].
Фазовая частотно-зависимая модель работает по принципу, согласно которому вся частотная зависимость системы передачи может быть представлена двумя матричными функциями передачи: функцией распространения H(ω) и характеристическим адмиттансом YC.
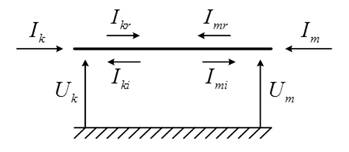
Рис. 1. Напряжения и токи в N-проводной линии передачи
Учитывая рис. 1, следующие выражения могут быть получены непосредственно из телеграфных уравнений [55]:
![]() ;
(1)
;
(1)
![]() ,
(2)
,
(2)
где
![]() – матричная функция
распространения;
– матричная функция
распространения;
![]() – матрица характеристического
адмиттанса;
– матрица характеристического
адмиттанса;
![]() – векторы напряжения на концах
узла k и m;
– векторы напряжения на концах
узла k и m;
![]() – векторы инжектируемого тока на
концах узла k и m;
– векторы инжектируемого тока на
концах узла k и m;
![]() – векторы падающего тока на
концах узла k и m;
– векторы падающего тока на
концах узла k и m;
![]() – векторы отраженного тока на
концах узла k и m.
– векторы отраженного тока на
концах узла k и m.
Матрицы H и YC рассчитываются несколько раз в дискретных точках в частотной области, а затем аппроксимируются и заменяются на эквивалентную рациональную функцию низкого порядка [3, 4, 6]. Такая методика позволяет использовать рекурсивный метод свертки для перехода во временную область, который является более вычислительно эффективными, чем вычисление интеграла свертки непосредственно [7].
Учет параметров проводника
Определение матриц Z и Y различается в зависимости от рассматриваемой системы. Рассмотрим получение данных матриц для воздушных электролиний.
Структура проводника воздушной линии приведена на рис. 2,
где μ – относительная магнитная проницаемость; ρ – удельное
сопротивление;
ri – радиус.
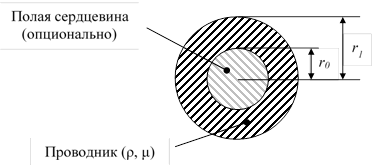
Рис. 2. Сечение проводника воздушной линии
При моделировании предполагается, что каждый проводник воздушной линии имеет идеальную цилиндрическую форму и может иметь полую сердцевину. Таким образом, проводник представляет собой сочетание внутренней и внешней поверхностных импедансов. Если проводник является сплошным, рассматривается только внешнее поверхностное сопротивление. Состав проводника предполагаются однородными, поэтому композитные провода, такие как сталеалюминевые кабели, должны быть аппроксимированы.
Последовательный импеданс Z для n воздушных линий задается следующим образом:
![]() , (3)
, (3)
где
![]() – матрица внутреннего
(собственного) импеданса;
– матрица внутреннего
(собственного) импеданса;
![]() – матрица обратного (земляного)
импеданса.
– матрица обратного (земляного)
импеданса.
Уравнение 3 может быть переписано в матричном виде:
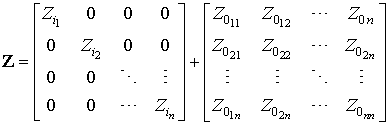 , (4)
, (4)
где
![]() – внутренний (собственный)
импеданс соответствующего проводника;
– внутренний (собственный)
импеданс соответствующего проводника;
![]() – взаимный обратный земляной
импеданс между проводниками j и
k.
– взаимный обратный земляной
импеданс между проводниками j и
k.
Расчет внутреннего импеданса для сплошных проводников осуществляется согласно формуле 5 [8]:
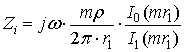 . (5)
. (5)
Для упрощения вычислений используются аналитические приближения к функциям Бесселя [9]:
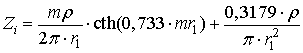 , (6)
, (6)
где
![]() – модифицированная функция
Бесселя первого рода;
– модифицированная функция
Бесселя первого рода;
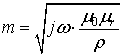 – обратная комплексная глубина
проникновения.
– обратная комплексная глубина
проникновения.
Матрица Y для воздушных линий передачи может быть получена, делая приближения, что окружающая линию среда (воздух) принимается идеальной (без потерь), а потенциал земли считается нулевым [10]:
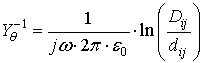 , (7)
, (7)
где
![]() – круговая частота;
– круговая частота;
![]() – диэлектрическая проницаемость
вакуума;
– диэлектрическая проницаемость
вакуума;
![]() ,
,![]() –
расстояния между проводниками (будут рассмотрены ниже).
–
расстояния между проводниками (будут рассмотрены ниже).
Рассмотрим расчет взаимного обратного импеданса.
Одним из самых известных методов для расчета обратного земляного импеданса для воздушных линий является метод Карсона [11]. Уравнение для взаимного импеданса между воздушными проводниками с учетом однородного возврата тока через землю записывается следующим образом:
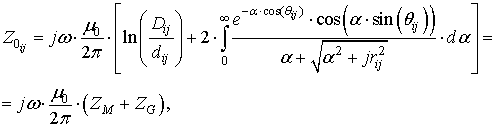 (8)
(8)
где
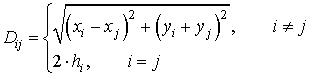
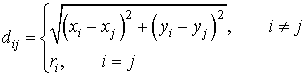
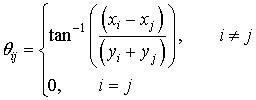
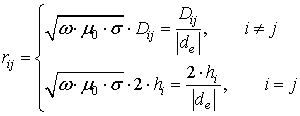
![]() ,
,![]() –
горизонтальное положение (координата) i-го и j-го проводников;
–
горизонтальное положение (координата) i-го и j-го проводников;
![]() ,
,![]() –
вертикальное положение (координата) i-го и j-го проводников;
–
вертикальное положение (координата) i-го и j-го проводников;
![]() – высота подъема i-го проводника;
– высота подъема i-го проводника;
![]() – радиус i-го
проводника;
– радиус i-го
проводника;
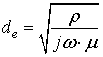 – глубина проникновения.
– глубина проникновения.
Имитационная модель локационного метода
Структурная схема разработанной модели приведена на рис. 3. Имитационная модель локационного метода состоит из двух основных блоков: блока генерации рефлектограмм и блока обработки рефлектограмм. Часть модели, связанная с генерацией рефлектограмм реализована в среде PSCAD/EMTDC; блок обработки данных – в среде MATLAB. Блок генерации позволяет получать рефлектограммы электролиний с прямолинейной и разветвленной топологиями с использованием трех видов зондирующих сигналов, а также рефлектограммы электролиний с основными видами повреждений (межфазные короткие замыкания, короткие замыкания на землю, обрывы). Обработка и анализ получаемых рефлектограмм осуществляется в среде MATLAB.
Блок генерации состоит из генератора зондирующего сигнала, подключенного к тестируемой электролинии, а также регистратора отраженного сигнала. Моделирование электролинии осуществляется с помощью фазовой частотно-зависимой модели, описанной выше. В результате работы блока генерации создаются две рефлектограммы линии: эталонная (без повреждения) и текущая (с имитацией аварии на линии).
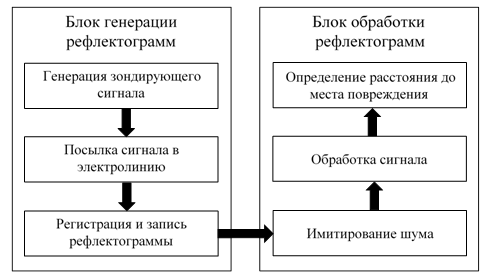
Рис. 3. Структурная схема имитационной модели локационного метода
Анализ полученных рефлектограмм осуществляется в блоке обработки. Обработка рефлектограмм включает в себя разностный анализ, автокорреляционную обработку, поиск места повреждения и вычисление расстояния до него. Блок обработки также позволяет исследовать локационный метод диагностики электролиний при различных отношениях сигнал/шум за счет добавления шумовых составляющих к получаемым сигналам.
Имитация шума осуществляется при помощи подмешивания к полученным эталонной и анализируемой рефлектограммам аддитивного белого гауссовского шума различной мощности; величина шума задается в децибелах по отношению к амплитуде полезного сигнала.
Разработанная имитационная модель позволяет использовать в качестве зондирующих сигналов не только одиночные импульсы, но и более сложные сигналы (ЛЧМ-импульс, код Баркера), позволяющие повысить точность определения расстояния до места повреждения [12].
Верификация имитационной модели локационного метода
Проверка адекватности разработанной модели локационного метода диагностики проведена путем сравнения модельных и экспериментальных рефлектограмм для импульсных реакций простейших неоднородностей.
1. Нагрузка в виде активного сопротивления различного номинала при согласованном волновом сопротивлении рефлектометра.
На рис. 4 приведены результаты моделирования. Видно, что при нагрузке с сопротивлением, меньшим чем волновое сопротивление линии, отраженный импульс меняет свою полярность. При сопротивлении, большем волнового сопротивления линии, импульс сохраняет полярность. При равенстве сопротивления нагрузки и волнового сопротивления отраженный импульс отсутствует. Полученные результаты моделирования соответствуют теоретическим ожиданиям и экспериментальным данным [13], приведенным на рис. 5.
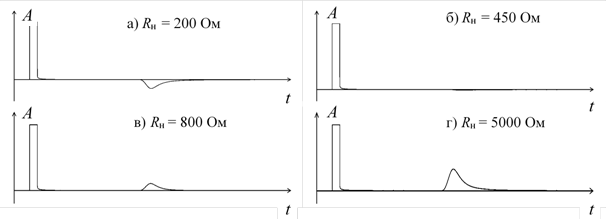
Рис. 4. Моделируемые рефлектограммы для одиночного провода при различной активной нагрузке на его конце

Рис. 5. Зависимость формы отраженного импульса от изменения величины резистивной нагрузки Rн на конце линии [13]
2. Холостой ход и короткое замыкание на конце провода при согласованном и рассогласованном волновом сопротивлении генератора.
На рис. 6 приведены результаты моделирования.
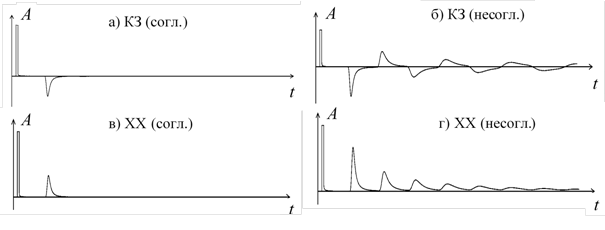
Рис. 6. Моделируемые рефлектограммы при
холостом ходе и коротком замыкании
а землю на конце провода при согласованном
и несогласованном сопротивлении рефлектометра
На приведенном выше рисунке видно, что отраженный импульс меняет свою полярность при коротком замыкании провода на землю и сохраняет полярность при холостом ходе. При отсутствии согласования рефлектометра с волновым сопротивлением линии возникают многочисленные переотражения импульса с уменьшением амплитуды и изменением формы. Уменьшение амплитуды возникает вследствие затухания, вносимого линией при многократном перемещении импульса по линии, а изменение формы вызвано фильтрующими свойствами линии (электролиния является фильтром низких частот).
Результаты имитационного моделирования импульсных реакций простейших неоднородностей электролинии совпадают с экспериментальными данными (рис. 7) [13].
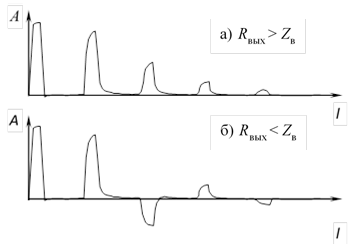
Рис. 7. Рефлектограммы при несогласованности выходного сопротивления рефлектометра с волновым сопротивлением линии [13]
Применение локационного метода диагностики для электролиний с разветвленной топологией
Для разветвленной электролинии картина отраженных импульсов существенно сложнее, чем для линий без ответвлений, вследствие многократных отражений от мест отпаек [14]. Одним из возможных методов автоматического обнаружения места повреждения такой линии с помощью локационного зондирования является разностный метод [15]. Суть метода заключается в следующем: создается эталонная рефлектограмма, которая снята при отсутствии повреждений на линии. Далее все измеряемые рефлектограммы сравниваются с эталонной, и первая точка на рефлектограмме, где имеется отличие от эталонной – и есть искомое место повреждения. На рис. 8 показан пример разностного анализа рефлектограммы поврежденной и неповрежденной линий. Из рисунка видно, что при вычитании все синхронные помехи компенсируются. По разностной рефлектограмме легко обнаружить отражение от места повреждения и определить расстояние L до него.
Существенным моментом является
распознавание отличий эталонной и текущей рефлектограмм, учитывая наличие шумов
в линии. Шумы в линии приводят к появлению отличий текущей рефлектограммы от
эталонной, могут приводить к ложному срабатыванию: достаточно большое случайное
отклонение текущей рефлектограммы от эталонной можно принять за отраженный от
места повреждения импульс. Поэтому необходимо определить некоторое пороговое
значение отклонения текущей рефлектограммы от эталонной, при превышении
которого мы с уверенностью говорим об обнаружении отраженного от места
повреждения импульса. Данное пороговое значение связано с уровнем шума в линии,
поэтому необходимо одновременно с записью эталонной рефлектограммы определить
уровень шума в линии.
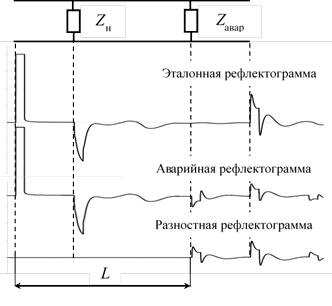
Рис. 8. Разностный анализ рефлектограммы
Алгоритм локализации повреждения можно описать последовательностью нескольких шагов: создание эталонной рефлектограммы, определение уровня шума в линии, обнаружение отраженного от места повреждения импульса.
Создание эталонной рефлектограммы и определение уровня шума в линии осуществляется следующим образом:
1. Накапливается n штук рефлектограмм Рэi(k), и создается эталонная рефлектограмма PЭ(k) по формуле:
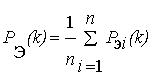 ,
k=1..p, (9)
,
k=1..p, (9)
где k – номер отсчета рефлектограммы, p – число отсчетов в рефлектограмме.
2. Определяется уровень шума s(q) для каждого окна q, для этого:
а) вычисляется усредненная текущая рефлектограмма PТ(k) из n штук полученных рефлектограмм линии Ртi(k):
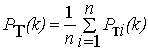 ,
k=1..p. (10)
,
k=1..p. (10)
б) подсчитывается отклонение рефлектограммы PТ(k) от эталонной РЭ(k) для каждого номера окна q:
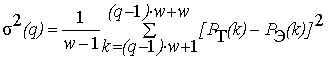 , (11)
, (11)
где w – длина окна, на котором вычисляется уровень шума.
Для обнаружения точки повреждения для каждого окна подсчитывается значение отклонения усредненной текущей рефлектограммы от эталонной и сравнивается с уровнем шума на данном окне s(q). При превышении отклонения в заданное число раз над уровнем шума s(q) – выявляется участок линии, на котором произошло повреждение.
Результаты моделирования для электролинии с разветвленной топологией
Исследование локационного метода для электролинии с разветвленной топологией осуществлено для электролинии с конфигурацией, приближенной к реальным подобным электролиниям (рис. 9).
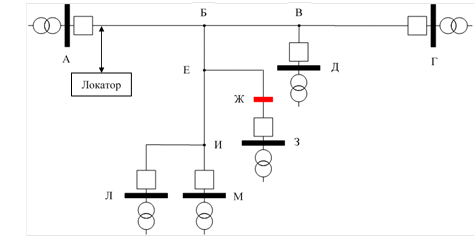
Рис. 9. Топология моделируемой электролинии с разветвленной структурой с обозначенным местом имитации аварии
Авария моделировалась на отпайке ЕЗ в точке Ж (расстоянии места подключения локатора – 61 км).
Эталонная рефлектограмма электролинии при отсутствии повреждений приведена на рис. 10.
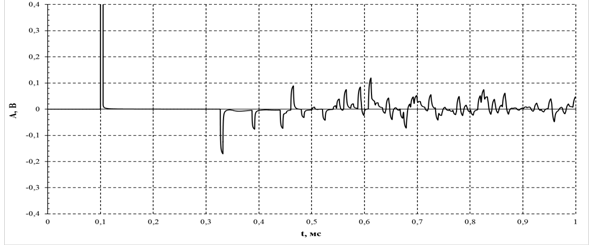
Рис. 10. Эталонная рефлектограмма моделируемой электролинии с разветвленной структурой
На эталонной рефлектограмме хорошо различимы лишь отражения от ближайших к началу линии мест ответвлений (точки Б, Е, В), а также от одного из концов электролинии (точка Д). С момента времени t = 0,6 мс (l = 75 км) рефлектограмма принимает шумоподобный характер, и выделить отдельные отражения от конкретных реперных точек на линии не представляется возможным.
На рис. 11 приведена рефлектограмма линии при моделировании однофазного короткого замыкания на землю.
На рис. 12 приведена рефлектограмма линии при моделировании межфазного замыкания.
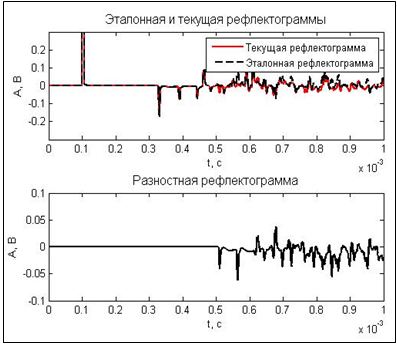
Рис. 11. Смоделированная рефлектограмма электролинии с разветвленной
структурой
при наличии повреждения в виде короткого замыкания фазы А на землю
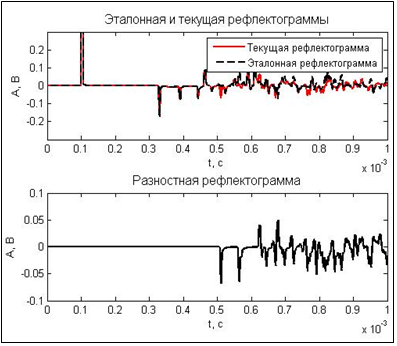
Рис. 12. Смоделированная рефлектограмма
электролинии с разветвленной структурой
при наличии повреждения в виде межфазного
короткого замыкания фаз А↔В
На рис. 13 приведена рефлектограмма линии при моделировании обрыва провода.
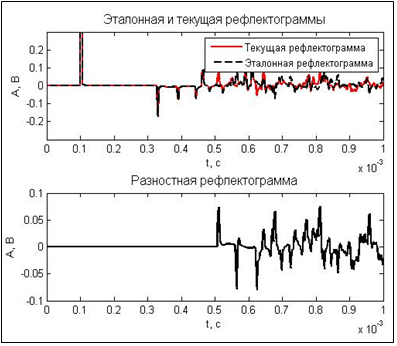
Рис. 13. Смоделированная рефлектограмма
электролинии с разветвленной
структурой при наличии повреждения в виде обрыва
провода фазы А
В зависимости от вида повреждения затухание отраженного сигнала составляет от 10 дБ до 20 дБ.
Определение расстояния до места повреждения осуществлялось за счет анализа разностной рефлектограммы поиском точки превышения амплитуды разностного сигнала некоторого порогового значения, зависящего от отношения сигнал/шум. В моделируемых условиях для всех случаев автоматически определенное расстояние составило 61,041 км и совпало с истинным (моделируемым) c погрешностью 0,07 %.
Заключение
1. Разработана имитационная модель локационного метода диагностики электролиний с произвольной древовидной топологией, позволяющей получать количественные оценки точности определения расстояния до места повреждения.
Модель разработана в программных средах PSCAD/EMTDC и MATLAB на основе фазовой частотно-зависимой модели электролинии. Модель позволяет учитывать характеристики проводов, характеристики среды, геометрию и структуру электролинии.
2. Результаты моделирования локационного метода продемонстрировали возможность обнаружения основных видов повреждений разветвленных электролиний (короткие замыкания на землю, межфазные замыкания и обрывы проводов) с погрешностью не более 0,07 % (при высоких отношениях сигнал/шум).
3. Получены количественные оценки затухания зондирующего сигнала в зависимости от вида повреждения.
Литература
1. Шалыт Г.М. Определение мест повреждения в электрических сетях. М.: Энергоиздат, 1982. 312 с.
2. Minullin R.G., Petrushenko Y.Y., Fardiev I.S. Sounding of Air Power Transmission Lines by the Location Method // Russian Electrical Engineering. 2008. Vol. 7. No. 79. pp. 389-396.
3. Morched A., Gustavsen B., Tartibi M. A Universal Model for Accurate Calculation of Electromagnetic Transients on Overhead Lines and Underground Cables // IEEE Transactions on Power Delivery. 1999. Vol. 14. No. 3. pp. 1032-1038.
4. Gustavsen B., Irwin G., Mangelrød R., Brandt D., Kent K. Transmission Line Models for the Simulation of Interaction Phenomena Between Parallel AC and DC Overhead Lines // Proceedings of IPST. Budapest. 1999. pp. 61-67.
5. Костенко М.В. Волновые процессы и электрические помехи в многопроводных линиях высокого напряжения. М.: Энергия, 1973. 272 с.
6. Gustavsen B., Semlyen A. Simulation of Transmission Line Transients Using Vector Fitting and Modal Decomposition // IEEE Transactions on Power Delivery. 1998. Vol. 13. No. 2. pp. 605-614.
7. Semlyen A., Dabuleanu A. Fast and Accurate Switching Transient Calculations on Transmission Lines with Ground Return Using Recursive Convolutions // IEEE Transactions on Power Apparatus and Systems. 1975. Vol. PAS-94. No. 2. pp. 561-571.
8. Schelkunoff S.A. The electromagnetic theory of coaxial transmission line and cylindrical shields // Bell Syst. Tech. J. 1934. No. 13. pp. 532-579.
9. Кузьмин Р.О. Бесселевы функции. Л.-М.: ГРОЛ, 1935. 151 с.
10. Wedepohl L.M. The Theory of Natural Modes in Multiconductor Transmission Systems: Course Notes. University of Manitoba, 2002.
11. Carson J.R. Wave Propagation in Overhead Wires with Ground Return // Bell Syst. Techn. J. 1926. Vol. 5. pp. 539-554.
12. Климов С.А. Метод повышения разрешающей способности радиолокационных систем при цифровой обработке сигналов // Журнал радиоэлектроники [электронный журнал]. 2013. No. 1. http://jre.cplire.ru/jre/jan13/1/text.pdf.
13. Минуллин Р.Г., Фардиев И.Ш. Локационная диагностика воздушных линий электропередачи. Казань: КГЭУ, 2008. 203 с.
14. Меркулов В.В., Синева И.С. О многократных отражениях в неоднородной линии передачи // Журнал радиоэлектроники [электронный журнал]. 2000. № 5. URL: http://jre.cplire.ru/jre/may00/1/text.pdf.
15. Закиров А.Н., Калабанов С.А., Карпов А.В., Шагиев Р.И. Концепция и разработка системы мониторинга и диагностики электролиний с древовидной топологией на базе «интеллектуального электромодема» // Ползуновский вестник. 2011. Т. 1. № 3. С. 114-117.