УДК 621.396.962
ЭКСПЕРИМЕНТАЛЬНАЯ ОЦЕНКА ЭФФЕКТИВНОСТИ РАЗРЕШЕНИЯ ГРУППОВЫХ ОБЪЕКТОВ С ИСПОЛЬЗОВАНИЕМ МЕТОДА СИНГУЛЯРНОГО РАЗЛОЖЕНИЯ И РЕГУЛЯРИЗАЦИИ ОБРАТНОГО ОПЕРАТОРА активной ЛОКАЦИОННОЙ СИСТЕМЫ
С. А. Климов, М. А. Свиридов
Военная академия войсковой ПВО Вооруженных Сил РФ имени Маршала Советского Союза А. М. Василевского
Статья поступила в редакцию 27 сентября 2016 г.
Аннотация. В статье представлены основные результаты экспериментальных исследований метода разрешения групповых объектов в условиях априорной неопределенности относительно числа и координат (дальности и азимута) отдельных объектов в группе. Исследуемый метод основан на сингулярном разложении и регуляризации матричного оператора активной локационной системы. Экспериментальные исследования доказали, что разрешение групповых объектов возможно реализовать достаточно простым в вычислительном отношении методом, позволяющим в реальном масштабе времени определить как число, так и координаты отдельных объектов в группе с помощью цифровой многоканальной активной локационной системы.
Ключевые слова: групповой объект, цифровая антенная решетка, сингулярное разложение, регуляризация, разрешающая способность, вероятность правильного разрешения.
Abstract. The main results of the pilot studies of a method of permission of group objects in the conditions of prior uncertainty of a directed number and coordinates (range and an azimuth) separate objects in group are provided. The researched method is based on singular expansion and regularization of the matrix operator of the active location system. The pilot studies prove that it is possible to realize permission of group objects by rather simple method in the computing relation allowing to define in real time both number and coordinates of separate objects in group by digital multi-channel active location system.
Keywords – group object, digital antenna grid, singular expansion, regularization, resolution capability, probability of the correct permission.
Теоретическое обоснование возможности разрешения групповых объектов (ГО) статистическими методами в условиях различных видов априорной неопределенности проведено в большом количестве работ [1–10]. Уточним, что под разрешением ГО в данном случае понимается оценивание числа и координат объектов, содержащихся в составе группового [5–10].
Как правило, результаты теоретических исследований подтверждаются с помощью имитационного математического моделирования. Заметно меньше имеется публикаций с результатами экспериментальных исследований, подтверждающих возможность разрешения ГО. В связи с этим актуальной является задача проведения экспериментальных исследований по разрешению ГО различными методами и оценке их эффективности.
Цель статьи – представить основные результаты экспериментальной оценки эффективности метода разрешения ГО, основанного на сингулярном разложении и регуляризации обратного оператора активной локационной системы в условиях априорной неопределенности относительно числа и координат (дальности и азимута) отдельных объектов в группе.
Эксперимент проводился на натурном макете линейной эквидистантной цифровой антенной решетки (ЦАР) акустического диапазона длин волн [11].
Структурная схема экспериментальной установки представлена на рисунке 1. Она включала в себя аналоговую и цифровую части.
Аналоговая часть состояла из генератора радиоимпульсов SIGLENT SDG-1010, источника питания BK Precision 1670A и линейной эквидистантной антенной решетки, состоящей из восьми ультразвуковых передатчиков (УЗП) MA40S4S, восьми ультразвуковых приемников (УЗПр) MA40S4T и восьми инструментальных усилителей AD622AR. Цифровая часть установки состояла из платы аналого-цифрового преобразователя (АЦП) ЛА-1,5PCI и ПЭВМ типа Pentium Dual-Core CPU E5700 3,00 ГГц.
Генератор SDG-1010 на несущей частоте 41 кГц (резонансная частота ультразвуковых элементов) вырабатывал последовательность радиоимпульсов. Длительность импульсов варьировалась от 3 до 10 мс, а период от 100 до 500 мс. Сформированный сигнал одновременно поступал на восемь ультразвуковых передатчиков, которые излучают его в пространство. Отраженный сигнал принимался восемью независимыми ультразвуковыми приемниками и усиливался при помощи инструментальных усилителей до требуемого уровня. Усиленный сигнал поступал на плату АЦП, где осуществлялось его аналого-цифровое преобразование. Сформированный в АЦП цифровой сигнал подвергался обработке в соответствии с требуемым алгоритмом разрешения сигналов.
>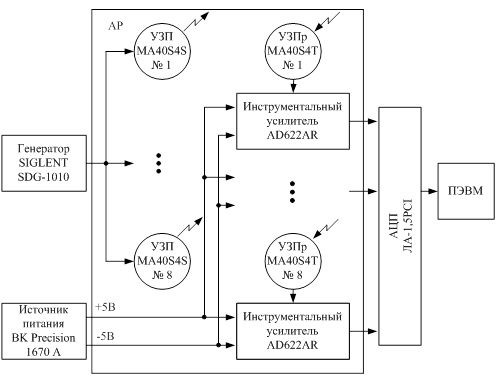
Рисунок 1 – Структурная схема экспериментальной установки
Внешний вид экспериментальной установки представлен на рисунке 2.

Рисунок 2 – Внешний вид экспериментальной установки.
а – общий
вид; б – антенная решетка; в – ультразвуковой приемный модуль
и инструментальный усилитель); г – ультразвуковой передатчик
Одной из задач при разработке экспериментальной установки было снижения требований к быстродействию АЦП. Эта задача обусловлена тем, что резонансная частота ультразвуковых элементов составляла 41 кГц. При этом для обработки сигнала использовались восемь независимых приемных каналов. С учетом теоремы Котельникова требуемая частота дискретизации должна была превышать 656 кГц, что значительно больше максимальной частоты дискретизации АЦП ЛА-1,5 PCI, которая составляет 500 кГц. Кроме того ясно, что снизив требования к быстродействию АЦП, можно также существенно уменьшить и объем вычислительных затрат.
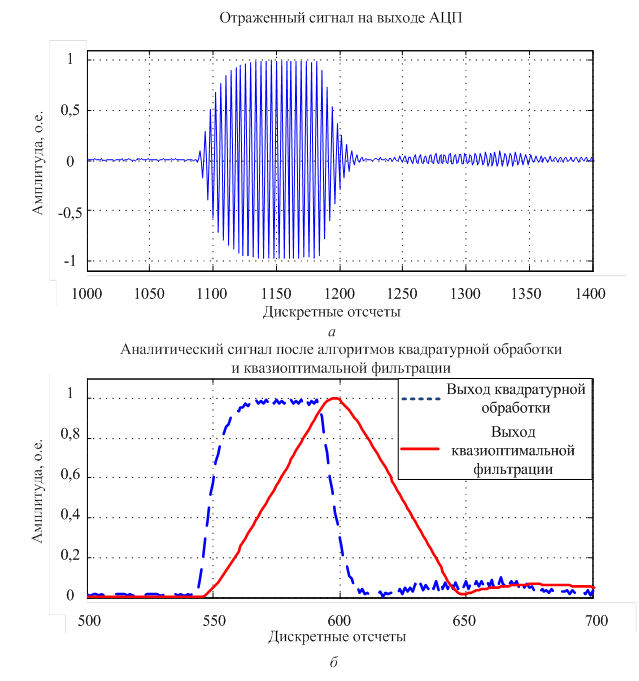
Рисунок 3 – Сигнала от одиночной точечной цели:
а –
нормированная амплитудная составляющая после алгоритма
получения квадратурных составляющих;
б – нормированная амплитудная составляющая после КОФ ОИ
При решении указанной задачи также рассматривался вопрос, связанный с возможностью получения с помощью одного АЦП двух квадратурных компонент действительного сигнала. Преимуществом данной процедуры обработки является одноканальность и, следовательно, исключение ошибок, связанных с неидентичностью двух каналов, недостатком - малое время преобразования аналогового отсчета в цифровую форму. Возможность снизить требования к быстродействию АЦП связана со стробоскопическим эффектом [12]. При проведении экспериментов удалось снизить требования к быстродействию АЦП в пять раз при несущей частоте зондирующего сигнала 41 кГц и частоте дискретизации 32,8 кГц.
Для проверки адекватности экспериментальной установки была осуществлена обработка простого радиоимпульса длительностью 3 мс, что составляло 110 отсчетов АЦП и, затем проведена его согласованная фильтрация по традиционному алгоритму. Истинное время запаздывания импульса составляло 1090 отсчетов АЦП. На рисунке 3, а представлен записанный сигнал с выхода АЦП от одиночного объекта. Дискретизация сигнала осуществлялась с частотой 32,8 кГц. Нормированная амплитудная составляющая сигнала после формирования квадратурных компонент представлена на рисунке 3, б. На этом же рисунке представлена нормированная амплитудная составляющая сигнала после квазиоптимальной фильтрации одиночного импульса (КОФ ОИ).
Из анализа рисунка 3, б следует, что максимум сигнала после КОФ ОИ находиться на отсчете АЦП с номером 595. Величина его, нормированная к энергии радиоимпульса, составляет значение близкое к единице, а длительность по основанию примерно составляет 110 отсчетов АЦП. При этом длительности по основанию амплитудной составляющей импульса до КОФ ОИ примерно равна 55 отсчетам. Такой результат обработки простого радиоимпульса хорошо известен. Заметим, что на рисунке 3, а представлен действительный сигнал, а на рисунке 3, б аналитический сигнал, соответствующий этому действительному сигналу, и результат его согласованной фильтрации. Поэтому длительность огибающей составляет 110, а не 220 отсчетов АЦП. Другими словами, длительность аналитического сигнала составляет всего 55 отсчетов. Это означает, что для последних происходит сокращение масштаба по оси времени в два раза, что необходимо было учитывать в эксперименте при измерении дальности до объектов.
Для оценки эффективности разрешения ГО по угловым координатам, большое значение имеет форма диаграммы направленности (ДН) антенной решетки. В экспериментальной установке была реализована цифровая линейная эквидистантная антенная решетка, состоящая из восьми идентичных ультразвуковых приемников, расположенных относительно друг друга на расстоянии 0,02 м. Диаграммы направленности отдельных передающих и приемных элементов представлены соответственно на рисунках 4, 5.
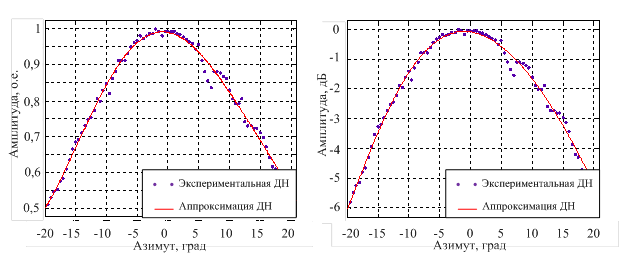
а б
Рисунок 4 – Диаграмма направленности одиночного ультразвукового передатчика:
а – в относительных единицах, б – в децибелах
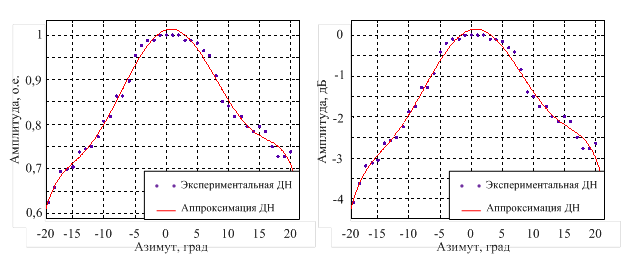
а б
Рисунок 5 – Диаграмма направленности одиночного ультразвукового приемника:
а – в относительных единицах, б – в децибелах
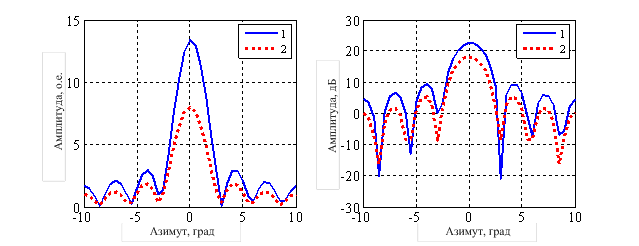
Диаграмма направленности ЦАР, представлена на рисунках 6, 7.
а б
Рисунок 6 – Рассчитанная диаграмма направленности
антенной решетки (2)
и модуль экспериментальной диаграммы направленности ЦАР (1):
а – в относительных единицах, б – в децибелах;
1 – модуль экспериментальной ДНА, 2 – рассчитанная ДНА
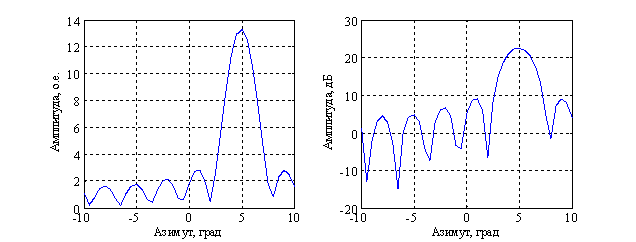
а б
Рисунок 7 – Диаграмма направленности ЦАР
(источник вторичного излучения располагается на азимуте 5 град):
а – в относительных единицах, б – в децибелах
Неидентичности комплексных коэффициентов передачи приемных каналов ЦАР приводили к искажению ее ДН. В связи с этим осуществлялась их коррекция. Коррекция выполнялась при расположении источника сигнала на нормали решетки. Корректирующие коэффициенты, вычисленные для этого направления, запоминались и использовались при приеме и коррекции сигналов с любых других направлений.
На рисунке 8 представлены синтезированные в ходе эксперимента ДН ЦАР на прием в азимутальной плоскости и пеленгационные характеристики измерителя угловых координат.
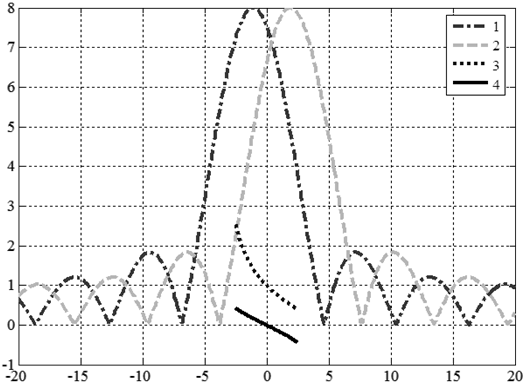
Рисунок 8 – Синтезированные в ходе эксперимента ДН ЦАР на прием в азимутальной плоскости
и пеленгационные характеристики измерителя угловых координат:
ДН первого канала (1), ДН второго канала (2), пеленгационная характеристика,
полученная методом отношения амплитуд (3), пеленгационная характеристика,
полученная суммарно-разностным методом (4)
Эксперименты проводились с различными источниками сигналов как активными (генераторы сигналов), так и пассивными, например, с квадратными пластинами и уголковыми отражателями с размерами граней, существенно превышающими длину ультразвуковой волны (рисунок 9). Последнее обеспечивало характер переотражения ультразвуковых колебаний от таких источников характерный для квазиотической области рассеяния электромагнитных волн в радиолокации. Количество источников составляло от двух до четырех. Статистическая обработка выполнялась по 100 реализациям, что обеспечило точность статистического эксперимента порядка 10 %.
|
а |
|
б |
|
в |
Рисунок 9 – Источники сигналов (эхосигналов) в
эксперименте:
а – генераторы сигналов; б – уголковые отражатели; в – прямоугольные
пластины
Эксперимент проводился в два этапа. На первом этапе осуществлялось разрешение ГО по дальности (сигналов по времени запаздывания) в отдельных каналах ЦАР. На втором этапе проводилось разрешение ГО по угловым координатам за счет разрешения ГО по дальности в отдельных каналах ЦАР амплитудным моноимпульсным методом пеленгации.
Разрешение ГО осуществлялось в условиях априорной неопределенности относительно числа и координат (дальности и азимута) отдельных объектов в группе. Исследуемый метод основан на сингулярном разложении и регуляризации матричного оператора активной локационной системы [13, 14].
Опишем кратко сущность указанного метода [13, 14].
Предположим, что активная локационная система (АЛС) представляет собой стационарную линейную многоканальную
пространственно-временную систему с узкополосным зондирующим сигналом и
математически описывается совокупностью из P измерительных каналов.
Каждому p-му каналу системы соответствует оператор преобразования с
известной характеристикой ![]() , где
, где ![]() – вектор параметров,
– вектор параметров, ![]() . В качестве составляющих вектора
. В качестве составляющих вектора ![]() могут быть время запаздывания, частота, направления
прихода и другие параметры сигналов. С физической точки зрения
могут быть время запаздывания, частота, направления
прихода и другие параметры сигналов. С физической точки зрения ![]() есть импульсная (частотная)
характеристика p-го канала АЛС, которую далее будет называть просто –
характеристикой.
есть импульсная (частотная)
характеристика p-го канала АЛС, которую далее будет называть просто –
характеристикой.
С учетом введенных предположений сигнал на выходе p-го канала многоканальной АЛС может быть записан в виде
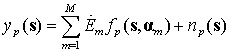 . (1)
. (1)
где ![]() – наблюдаемый сигнал в p-м измерительном канале АЛС;
– наблюдаемый сигнал в p-м измерительном канале АЛС;
![]() – известная характеристика p-го измерительного канала АЛС;
– известная характеристика p-го измерительного канала АЛС; ![]() – область определения вектора
– область определения вектора ![]() ;
; ![]() –
область поля параметров вектора
–
область поля параметров вектора ![]() ;
;
![]() – комплексная
амплитуда m-го сигнала, соответствующая точке
– комплексная
амплитуда m-го сигнала, соответствующая точке ![]() области
поля параметров
области
поля параметров ![]() ; М – число сигналов в
составе смеси;
; М – число сигналов в
составе смеси;
![]() – шумы наблюдения в p-м измерительном канале.
– шумы наблюдения в p-м измерительном канале.
Из
выражения (1) следует, что множество из ![]() измерительных
каналов АЛС и М сигналов можно записать в виде системы уравнений
измерительных
каналов АЛС и М сигналов можно записать в виде системы уравнений
![]() ,
(2)
,
(2)
где ![]() –
– ![]() -вектор-столбец
измеренных напряжений на выходе
-вектор-столбец
измеренных напряжений на выходе ![]() измерительных каналов
РЛС;
измерительных каналов
РЛС; ![]() –
– ![]() -матрица
характеристик каналов РЛС;
-матрица
характеристик каналов РЛС; ![]() –
– ![]() -вектор-столбец
комплексных амплитуд сигналов;
-вектор-столбец
комплексных амплитуд сигналов;
![]() –
– ![]() -вектор-столбец шумов наблюдения.
-вектор-столбец шумов наблюдения.
Задача, заключающаяся
в получении решения системы уравнений (2) при неизвестном одновременно числе
сигналов ![]() , их амплитудах
, их амплитудах ![]() и
векторе параметров
и
векторе параметров ![]() в ходе единого вычислительного
процесса является некорректной. Действительно, из выражения (2) следует, что
вид матрицы
в ходе единого вычислительного
процесса является некорректной. Действительно, из выражения (2) следует, что
вид матрицы ![]() известен,
но ее конкретные значения зависят от неизвестного вектора параметров
известен,
но ее конкретные значения зависят от неизвестного вектора параметров ![]() , а ее размерность – от неизвестного числа
сигналов M в составе смеси сигналов и шума. Вместе с тем, для
решения системы уравнений (2) значения матрицы
, а ее размерность – от неизвестного числа
сигналов M в составе смеси сигналов и шума. Вместе с тем, для
решения системы уравнений (2) значения матрицы ![]() должны быть известны заранее.
Наличие шумов наблюдения во входном сигнале приводит к несовместности системы
уравнений (2). Получить строгое решение такой системы уравнений невозможно
принципиально и приходится выбирать то или иное псевдорешение, обеспечивающее
его единственность и устойчивость.
должны быть известны заранее.
Наличие шумов наблюдения во входном сигнале приводит к несовместности системы
уравнений (2). Получить строгое решение такой системы уравнений невозможно
принципиально и приходится выбирать то или иное псевдорешение, обеспечивающее
его единственность и устойчивость.
Реализовать совместность системы
уравнений (2) возможно, если выполнить такое преобразование с вектором ![]() , которое обеспечит его
принадлежность к образу матрицы
, которое обеспечит его
принадлежность к образу матрицы ![]() . Такое преобразование
предлагается осуществлять в виде
. Такое преобразование
предлагается осуществлять в виде ![]() , где
, где ![]() – псевдообратная матрица [15]. Другими словами, матрица
– псевдообратная матрица [15]. Другими словами, матрица ![]() в этом
случае будет ортогональным проектором для матрицы
в этом
случае будет ортогональным проектором для матрицы ![]() на
подпространство, образованное линейной оболочкой ее вектор-столбцов, т. е.
образом матрицы
на
подпространство, образованное линейной оболочкой ее вектор-столбцов, т. е.
образом матрицы ![]() . Это и позволяет обеспечить
совместность системы уравнений (2). Обеспечить единственность и
устойчивость решения значительно сложнее.
. Это и позволяет обеспечить
совместность системы уравнений (2). Обеспечить единственность и
устойчивость решения значительно сложнее.
Предположим, что в составе
сигнальной смеси присутствуют P сигналов с амплитудами ![]() ,
, ![]() . Такое предположение является закономерным
и ограничивает сверху максимальное число разрешаемых сигналов, которое не
превосходит числа уравнений в системе (2). Часть амплитуд
. Такое предположение является закономерным
и ограничивает сверху максимальное число разрешаемых сигналов, которое не
превосходит числа уравнений в системе (2). Часть амплитуд ![]() при этом может быть равна нулю. Связано
это с тем, что в составе сигнальной смеси может присутствовать разное число
сигналов, но предполагается, что
при этом может быть равна нулю. Связано
это с тем, что в составе сигнальной смеси может присутствовать разное число
сигналов, но предполагается, что ![]() . Практическая польза этого
заключается в том, что позволяет зафиксировать размерность матрицы
. Практическая польза этого
заключается в том, что позволяет зафиксировать размерность матрицы ![]() и получить решение
системы уравнений (2). Кроме того, при неизвестном
векторе параметров
и получить решение
системы уравнений (2). Кроме того, при неизвестном
векторе параметров ![]() в силу постулата Байеса [16]
целесообразно предположить, что для разрешаемых сигналов они распределены
равномерно. С учетом этих предположений мы можем сформировать вектор параметров
в силу постулата Байеса [16]
целесообразно предположить, что для разрешаемых сигналов они распределены
равномерно. С учетом этих предположений мы можем сформировать вектор параметров
![]() . В качестве составляющих
. В качестве составляющих ![]() p-го вектора
p-го вектора ![]() могут быть приняты ожидаемые время
запаздывания, частота, направления прихода и другие параметры p-го сигнала,
где
могут быть приняты ожидаемые время
запаздывания, частота, направления прихода и другие параметры p-го сигнала,
где ![]() ,
I – число параметров. При гипотезе о равномерном
распределении параметров сигналов элементы
,
I – число параметров. При гипотезе о равномерном
распределении параметров сигналов элементы ![]() матрицы
матрицы
![]() определяются выбранным шагом
определяются выбранным шагом ![]() по i-му
параметру между l-м и
k-м сигналами
по i-му
параметру между l-м и
k-м сигналами ![]() в области определения поля параметров
в области определения поля параметров ![]() вектора
вектора ![]() . Шаг
по параметру
. Шаг
по параметру ![]() должен удовлетворять условию
должен удовлетворять условию ![]() , где
, где ![]() –
элемент разрешения по i-му параметру сигнала,
–
элемент разрешения по i-му параметру сигнала, ![]() . В этом случае
матрица
. В этом случае
матрица ![]() определена и решение системы уравнений (2)
относительно комплексных коэффициентов
определена и решение системы уравнений (2)
относительно комплексных коэффициентов ![]() также
становится единственным. С учетом введенных предположений матрица характеристик
каналов РЛС теперь не зависит от М, а ее размерность составит
также
становится единственным. С учетом введенных предположений матрица характеристик
каналов РЛС теперь не зависит от М, а ее размерность составит ![]() .
.
Дальнейший
ход рассуждений опирается на важнейшую теорему линейной алгебры. Смысл
ее заключается в том, что образ любого вектора при преобразовании может быть
найден, если известны сингулярные числа и сингулярные базисы этого
преобразования [17]. В соответствии с этим найдем
сингулярное разложение матрицы ![]() , которое будет иметь вид
, которое будет иметь вид
![]() ,
(3)
,
(3)
где ![]() – унитарная матрица
порядка
– унитарная матрица
порядка ![]() ;
;
![]() – диагональная
– диагональная ![]() -матрица
сингулярных значений
-матрица
сингулярных значений ![]() матрицы
матрицы ![]() ;
;
![]() – унитарная матрица порядка
– унитарная матрица порядка ![]() .
.
На основании теорем о
сингулярном разложении и понятии псевдообратной матрицы
Мура – Пенроуза получим псевдообратную ![]() -матрицу
-матрицу
![]() сингулярных значений матрицы характеристик
каналов РЛС
сингулярных значений матрицы характеристик
каналов РЛС ![]() . Для
матрицы
. Для
матрицы ![]() псевдообратной является матрица
псевдообратной является матрица ![]() . Тогда псевдообратная
. Тогда псевдообратная ![]() -матрица характеристик
каналов РЛС
-матрица характеристик
каналов РЛС ![]() будет иметь вид
будет иметь вид
![]() .
(4)
.
(4)
Псевдорешение системы
уравнений (2) будем искать среди решений системы вида ![]() , откуда с учетом с
учетом выражения (4) получим
, откуда с учетом с
учетом выражения (4) получим
![]() .
(5)
.
(5)
В ходе
функционирования РЛС для тех элементов разрешения, в которых принято решение об
обнаружении сигнала реализуется операция векторно-матричного умножения (5) и
сравнение полученного вектора с порогом ![]() , где
, где ![]() – порог. Элементы вектора
– порог. Элементы вектора ![]() , которые удовлетворяют условию превышения порога,
считаются решением (2). Последнее также можно трактовать как физически
обоснованное требование учета тех сигналов, амплитуда которых превышает в
заданное число раз среднеквадратичное значение шума. Количество
этих элементов определяет оценку числа эхосигналов
, которые удовлетворяют условию превышения порога,
считаются решением (2). Последнее также можно трактовать как физически
обоснованное требование учета тех сигналов, амплитуда которых превышает в
заданное число раз среднеквадратичное значение шума. Количество
этих элементов определяет оценку числа эхосигналов ![]() ,
сформировавших вектор наблюдения
,
сформировавших вектор наблюдения ![]() , а их положение – оценку вектора параметров
, а их положение – оценку вектора параметров ![]() сигналов.
сигналов.
Обратим внимание на один
важный момент, имеющий принципиальное значение для предлагаемого метода. Выбранный
сингулярный базис ![]() матрицы характеристик каналов
РЛС
матрицы характеристик каналов
РЛС ![]() позволяет не только обеспечить существования решения. При практической
реализации метода он позволяет исключить зависимость решения от априорного знания
числа разрешаемых сигналов, поскольку как следует из выражений (3, 4)
размерность сингулярного базиса
позволяет не только обеспечить существования решения. При практической
реализации метода он позволяет исключить зависимость решения от априорного знания
числа разрешаемых сигналов, поскольку как следует из выражений (3, 4)
размерность сингулярного базиса ![]() не зависит от М,
а определяется только числом каналов Р матрицы характеристик
не зависит от М,
а определяется только числом каналов Р матрицы характеристик ![]() .
.
Таким образом, в предлагаемом методе разрешения устойчивость решения обеспечивается за счет исключения из пространства решений тех направлений, в которых отношение сигнала к шуму не превышает некоторого порогового значения по причине малых значений соответствующих сингулярных чисел матрицы оператора локационной системы, а также отсутствия составляющих сигнала в указанных направлениях. Из этого следует, что для обеспечения устойчивости решения принципиальным является вопрос о выборе числа каналов Р. Он должен осуществляться на компромиссной основе, поскольку можно показать [13], что диагональные элементы корреляционной матрицы оценки (5) определяются выражением
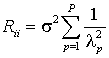 , (6)
, (6)
где ![]() –
дисперсия шума. Из выражения (6) следует, что
повышение разрешающей способности (увеличение
–
дисперсия шума. Из выражения (6) следует, что
повышение разрешающей способности (увеличение ![]() )
требует увеличения отношения сигнал-шум, т. к. с ростом
)
требует увеличения отношения сигнал-шум, т. к. с ростом ![]() сингулярные числа
сингулярные числа ![]() быстро убывают,
быстро убывают,
а дисперсия оценок увеличивается как ![]() .
.
Таким
образом, регуляризация решения системы уравнений (2) заключалась в обоснованном
выборе по какому-либо критерию числа каналов Р и, соответственно числа
сингулярных значений ![]() , определяющих устойчивость
решения (2). В ходе эксперимента критерием выбора числа сингулярных значений
, определяющих устойчивость
решения (2). В ходе эксперимента критерием выбора числа сингулярных значений ![]() был вид формы характеристики канала и
ограничение на рост отношения сигнал-шум.
был вид формы характеристики канала и
ограничение на рост отношения сигнал-шум.
На рисунке 10 показаны зависимости роста отношения сигнал-шум от
размерности сингулярного базиса P для различных видов характеристик каналов АЛС. На нем по
оси абсцисс отложено значение размерности сингулярного базиса P (число каналов АЛС), а по оси ординат величина ![]() в логарифмическом масштабе. Из них следует, что наилучшими
потенциальными возможности для разрешения обладает характеристика, близкая к
прямоугольному виду, при этом число каналов рационально ограничить 10–15. В
этом случае рост потребного отношения сигнал-шум не превышает 10 дБ.
в логарифмическом масштабе. Из них следует, что наилучшими
потенциальными возможности для разрешения обладает характеристика, близкая к
прямоугольному виду, при этом число каналов рационально ограничить 10–15. В
этом случае рост потребного отношения сигнал-шум не превышает 10 дБ.
При проведении натурного эксперимента оценка разрешающей способности по
дальности предполагала вычисление вероятности правильного разрешения ![]() парного ГО при ограниченном сверху значении
ложных решений
парного ГО при ограниченном сверху значении
ложных решений ![]() , не превышающих 0,1. Оценки
, не превышающих 0,1. Оценки ![]() проводились для различных относительных
рассогласований источников сигналов по дальности и угловым координатам,
различной относительной интенсивности эхосигналов источников и отношений
сигнал-шум. Диапазон отношений сигнал-шум составлял 10–40 дБ.
проводились для различных относительных
рассогласований источников сигналов по дальности и угловым координатам,
различной относительной интенсивности эхосигналов источников и отношений
сигнал-шум. Диапазон отношений сигнал-шум составлял 10–40 дБ.
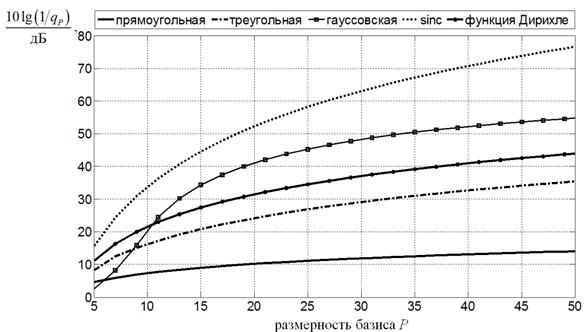
Рисунок 10 – Рост отношения сигнал-шум в зависимости от размерности
сингулярного базиса P и вида характеристик каналов АЛС
Результаты, демонстрирующие характер
изменения вероятностей ![]() для разных относительных
рассогласований источников эхосигналов по дальности при фиксированном
относительном угловом расстоянии между источниками по угловым координатам после обработки
исследуемым методом разрешения ГО представлены на рисунке 11. В данном
случае в качестве источников эхосигнала выступали квадратные пластины, которые
переотражения ультразвуковые зондирующие сигналы, формируемые ЦАР. Вертикальными линиями на графиках рисунка 11
показана величина доверительного интервала с доверительной вероятностью 0,9.
для разных относительных
рассогласований источников эхосигналов по дальности при фиксированном
относительном угловом расстоянии между источниками по угловым координатам после обработки
исследуемым методом разрешения ГО представлены на рисунке 11. В данном
случае в качестве источников эхосигнала выступали квадратные пластины, которые
переотражения ультразвуковые зондирующие сигналы, формируемые ЦАР. Вертикальными линиями на графиках рисунка 11
показана величина доверительного интервала с доверительной вероятностью 0,9.
Анализ результатов, представленных на рисунке 10, позволяет сделать следующий вывод. Результаты экспериментальных исследований доказали существенно более высокую эффективность предлагаемого метода разрешения ГО по сравнению со стандартной корреляционной (фильтровой) обработкой. Так при отношении сигнал-шум не менее 26 дБ наблюдалось превышение рэлеевского предела разрешающей способности по дальности от двух до четырех раз.
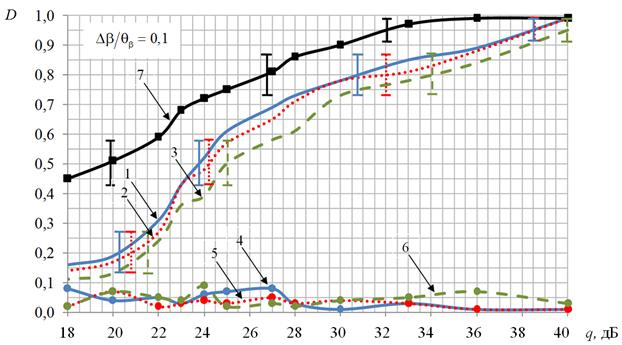
Рисунок 11 – Зависимость вероятности
правильного разрешения ![]() двух целей
двух целей
от отношения сигнал-шум q, полученные по результатам натурного
эксперимента:
![]() (1),
(1), ![]() (2) и
(2) и ![]() (3). Число каналов измерения P = 10
(3). Число каналов измерения P = 10
Вероятность ложных решений ![]() для графиков (1–3)
графики (4–6) соответственно.
для графиков (1–3)
графики (4–6) соответственно.
Вероятность правильного обнаружения одной цели (7)
При проведении натурного эксперимента по оценке разрешающей способности по дальности и угловым координатам строились двумерные пространственно-временные диаграммы, на которых отображались как истинные положения источников сигналов по указанным координатам и их оценки в текущем измерении, так и статистические характеристики оценок: математического ожидания (МОЖ) и среднеквадратичного отклонения (СКО).
Пространственно-временные диаграммы строились для различных относительных
рассогласований источников сигналов по угловым координатам и дальности при
фиксированном значении отношения сигнал-шум
и вероятности ложных решений не более 0,1.
Результаты, демонстрирующие характер изменения полученных оценок по
дальности и угловым координатам представлены на рисунках 12, 13.
В качестве источников эхосигнала выступали квадратные
пластины, которые переотражения ультразвуковые зондирующие сигналы, формируемые
ЦАР.
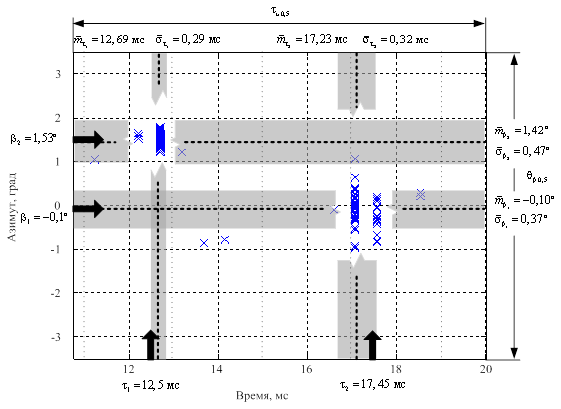
а
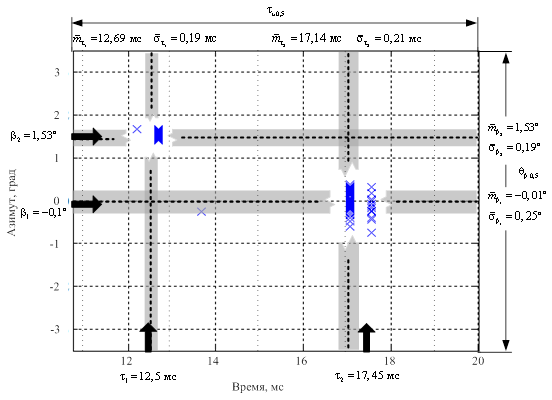
б
Рисунок 12 – Пространственно-временная диаграмма результатов
статистической обработки разрешения двух целей по дальности
и угловым координатам, полученная при проведении натурного эксперимента.
P = 10; ![]() ;
; ![]() . Вероятность
ложных тревог
. Вероятность
ложных тревог ![]() :
:
а – отношение сигнал-шум 26 дБ; б – отношение сигнал-шум 30 дБ
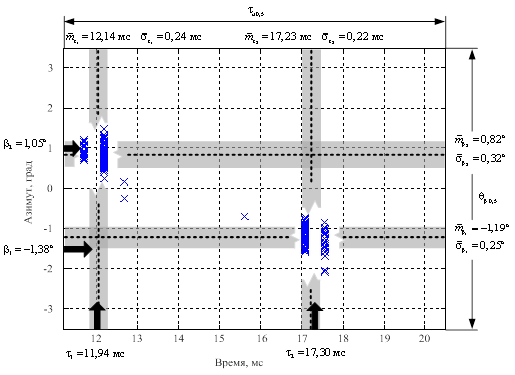
а
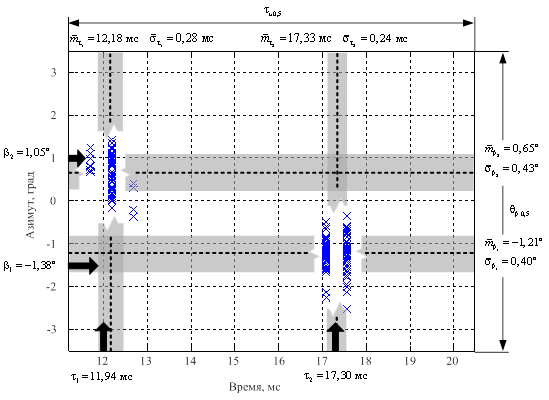
б
Рисунок 13 – Пространственно-временная диаграмма результатов
статистической обработки разрешения двух целей по дальности и
угловым координатам,
полученная при проведении натурного эксперимента.
P = 10; ![]() ;
; ![]() . Вероятность
ложных тревог
. Вероятность
ложных тревог ![]() :
:
а – отношение сигнал-шум 26 дБ; б – отношение сигнал-шум 30 дБ
На рисунках 12, 13 стрелками показаны истинные положения источников, пунктирными линиями – оценки МОЖ, полосами серого цвета – СКО оценок и крестиками – оценки пространственно-временного положения источников в текущем измерении. Кроме того, на всех диаграммах приведены числовые характеристики, как сигналов, так и оценок, полученных в результате статистической обработки. Вертикальный размер диаграммы соответствует ширине диаграммы направленности ЦАР, горизонтальный – длительности зондирующего импульса. Таким образом, область, отображаемая на диаграмме это двумерный пространственно-временной элемент разрешения для ЦАР.
Анализ результатов, представленных на рисунках 12, 13 позволяет сделать следующие выводы.
Результаты экспериментальных исследований доказывают существенно более высокую эффективность предлагаемого метода разрешения ГО по сравнению со стандартной пространственно-временной обработкой. Так при отношениях сигнал-шум не менее 26 дБ наблюдалось превышение рэлеевского предела разрешающей способности по дальности в два–четыре раза, а по угловой координате в два–три раза. При этом оценки пространственно-временного положения отдельных источников эхосигналов на плоскости «угол-дальность» с высокой степенью точности соответствовали их истинным значениям.
Таким образом, экспериментальные исследования доказали, что разрешение ГО возможно реализовать достаточно простыми в вычислительном отношении методами, позволяющими определять как число, так и координаты отдельных объектов в группе в реальном масштабе времени с помощью цифровой многоканальной активной локационной системы.
Видеозаписи экспериментов прилагаются отдельными файлами к статье:
Литература
1. Ширман Я. Д. Теория обнаружения полезного сигнала на фоне гауссовых шумов и произвольного числа мешающих сигналов со случайными амплитудами и начальными фазами // Радиотехника и электроника. 1959. Т. 4. № 12. С. 1176-1192.
2. Ширман Я. Д. Статистический анализ оптимального разрешения // Радиотехника и электроника. 1961. Т. 6. .№ 8. С. 1237-1246.
3. Nilsson N. J. On the optimum range resolution of radar signals in noise. IRE Trans. Information Theory, vol. IT-7, Oct. 1961, pp. 245–253.
4. Хелстром К. Статистическая теория обнаружения сигналов. М., Изд-во иностр. лит., 1963. 432 с.
5. Ширман Я. Д. Разрешение и сжатие сигналов. М., Сов. радио, 1974. 315 с.
6. Царьков Н. М. Многоканальные радиолокационные измерители. М., Сов. радио, 1980. 192 с.
7. Шинаков Ю. С., Сперанский
В. С. Совместное обнаружение, разрешение и измерение параметров сигналов на
фоне помехи на выходе антенной решетки. Синтез алгоритмов //
Радиотехника и
электроника. 1982. Т. 27. № 11.
С. 2179–2184.
8. Трифонов А. П., Шинаков Ю. С. Совместное различение сигналов и оценка их параметров на фоне помех. М., Радио и связь, 1986. 264 с.
9. Курикша А. А. Оценка числа и параметров компонент сигнала при наличии шума//Радиотехника и электроника. 1984. Т. 29. № 9. С. 1740-1744.
10. Коновалов Л. Н. Определение числа сигналов методом проверки сложных гипотез по критерию отношения правдоподобия // Радиоэлектроника. 1988. Т. 31. № 7. С. 18-24.
11. Климов С А., Свиридов М. А. Результаты экспериментальных исследований разрешения сигналов с использованием регуляризации для систем линейных уравнений / Сб. науч. ст. по материалам ХХII Международной науч.-технич. конф. «Радиолокация, навигация, связь». – Воронеж: ВГУ, 2016. С. 1024–1034.
12. Цифровые радиоприемные системы. Справочник / Под ред. М. И. Жодзишского. М., Радио и связь, 1990. 208 с.
13. Климов С. А. Метод разрешения групповых радиолокационных объектов // Электромагнитные волны и электронные системы. 2013. Т. 18. № 4. С. 28–37.
14. Климов С. А. Измерение угловых координат отдельных целей из состава групповой в радиолокационной системе с моноимпульсным пеленгатором // Вопр. радиоэлектроники. Сер. радиолокационная техника. – 2014. – Вып. 3. – С. 142–147.
15. Хорн, Р. Матричный анализ / Р. Хорн, Ч. Джонсон. - М.: Мир, 1990. - 655 с.
16. Теребиж, В. Ю. Введение в статистическую теорию обратных задач / В. Ю. Теребиж. – М.: Физматлит, 2005. – 376 с.
17. Беклемишев, Д. В. Дополнительные главы линейной алгебры / Д. В. Беклемишев. - М.: Наука, 1983. – 336 с.


