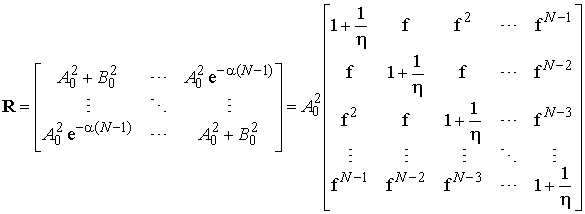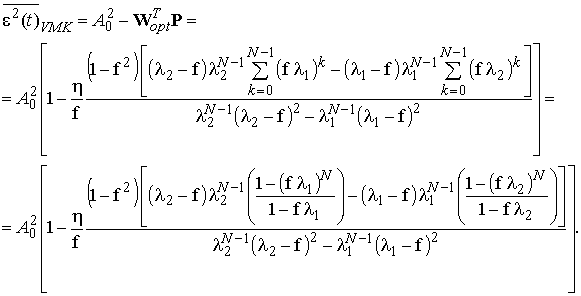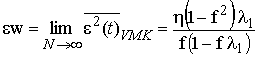УДК 681.513.6
Метод компенсации помех на основе векторно-матричных преобразований
А. Е. Манохин
Институт радиоэлектроники и информационных технологий-РТФ
УрФУ им. первого Президента РФ Б.Н.Ельцина,
кафедра радиоэлектронных и
телекоммуникационных систем, Екатеринбург
Статья поступила в редакцию 4 июля 216 г.
Аннотация. В работе решается задача выделения непрерывных (гауссовых) и импульсных (симметричных) сигналов на фоне непрерывных (гауссовых) и импульсных (симметричных) помех с помощью метода компенсации на основе векторно-матричных преобразований (уравнения Винера-Хопфа). Отличительной особенностью метода является отсутствие обязательного требования к взаимной некоррелированности помех в каналах. Благодаря этому, компенсатор помех, реализующий данный метод, можно построить по одноканальной схеме. Установлено, что при компенсации белого гауссова шума или импульсной помехи выигрыш в отношении мощности сигнал–помеха на выходе векторно-матричного компенсатора может достигать 18 дБ. Наихудшая компенсация происходит при совпадении частотных спектров сигнала и помехи. Наличие дисбаланса дисперсий помех в каналах негативно влияет на выделение полезного сигнала.
Ключевые слова: уравнение Винера-Хопфа, векторно-матричный компенсатор, корреляционная матрица, симметричный телеграфный процесс.
Abstract. A problem of extracting continuous (gaussian) and pulse (symmetric) signals on a background of continuous (gaussian) and pulse (symmetric) disturbances with using a method based on vector-matrix transformation (Wiener-Hopf equation) is decided in the work. The distinction of the method is an absence of demand on mutually uncorrelated disturbances in channels. Thanks to it, a disturbances canceller, realizing the method, can be made on single channel scheme. It is established that the gain in signal-to–noise at the output of the vector-matrix canceller can reach 18 dB if white Gaussian noise or impulse noise is cancelled. The worst cancellation occurs when frequency spectra of the signal and disturbance is congruous. An imbalance of disturbance variances in the channels affects the extraction of the desired signal.
Key words: Wiener-Hopf equation, the vector-matrix canceller, a correlation matrix, a symmetric telegraph process.
Постановка задачи
Для синтеза метода компенсации помех на основе векторно-матричных преобразований использован метод оценки весовых коэффициентов адаптивного фильтра в соответствии с решением векторно-матричного уравнения Винера-Хопфа по критерию наименьшего среднеквадратического отклонения полезного сигнала от его оценки [1]:
где R — корреляционная матрица входного сигнала адаптивного фильтра, P — вектор взаимокорреляционной функции отсчетов входного и полезного сигнала.
При независимости полезного сигнала и помехи вектор P есть не что иное, как вектор автокорреляционной функции полезного сигнала, т. е.
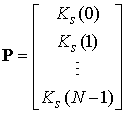(2)
где Ks — автокорреляционная функция процесса s(n)
Если имеется возможность сформировать подходящий опорный канал (назовем его идеальным), в котором действует помеха d2, совпадающая по корреляционной функции, но взаимно некоррелированная с помехой d1 в основном канале, то вектор Р можно получить с помощью разности автокорреляционных векторов зашумленного сигнала Ps+d1 и помехи в опорном канале Pd2:
(3)
Подставляя разность автокорреляционных векторов (3) в (1), оптимальный вектор, полученный с помощью синтезированного метода, можно записать:
(4)
В отличие от компенсатора Уидроу [1] в представленном методе отсутствует обязательное требование к взаимной некоррелированности помех в каналах. Исходя из этого, можно построить компенсатор на основе векторно-матричных преобразований по упрощенной (одноканальной) схеме.
Формирование структурной схемы компенсатора
Пусть дискретный зашумленный сигнал (смесь полезного сигнала и помехи), действующий на входе компенсатора, представляется как
(5)
где s(n) и d(n) – взаимно некоррелированные, центрированные вещественные независимые стационарные случайные процессы с единичной дисперсией.
Составим корреляционную матрицу входного сигнала NxN:
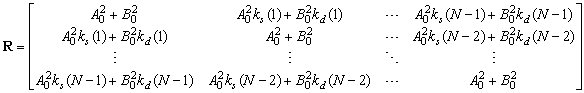(6)
и автокорреляционный вектор опорной помехи:
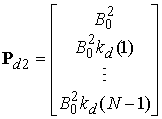(7)
где ks и kd — нормированные к дисперсии автокорреляционные функции процессов s(n) и d(n) соответственно; N — размер автокорреляционных функций ks и kd.
Затем сформируем автокорреляционный вектор входного сигнала y(n):
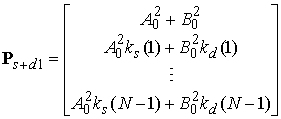(8)
Подставляя разность автокорреляционных векторов (8) и (7) и обратную корреляционную матрицу (6) в (4), получаем оптимальный вектор:
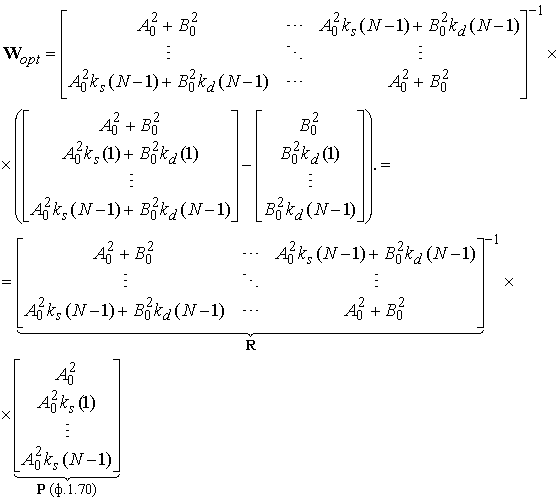
Структурная схема, реализующая компенсационные методы на основе векторно-матричных преобразований, изображена на рис. 1.
Вычисление R и P происходит при замыкании К2 и размыкании К1. В то же время опорный канал формируется с помощью замыкания переключателя К1 и размыкания К2, когда во входном сигнале отсутствует полезный сигнал и действует только помеха.
После формирования оптимального вектора коэффициенты переписываются в фильтр, на входе которого действует зашумленный сигнал, а на выходе формируется оценка полезного сигнала.
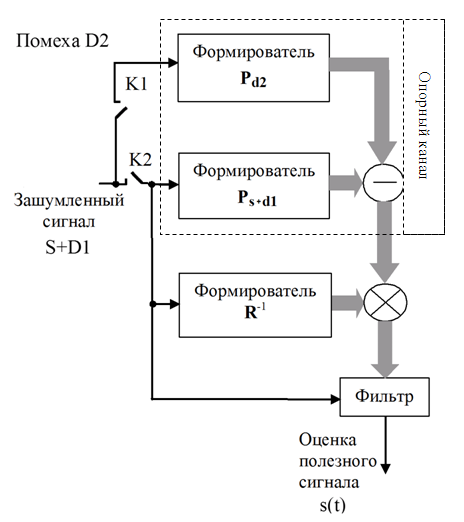
Рис. 1. Векторно-матричный компенсатор
Таким образом, при идеальном опорном канале векторно-матричный компенсатор формирует оптимальный фильтр Винера по критерию наименьшего среднеквадратичного отклонения выходного сигнала от полезного.
Интерес к компенсации непрерывных помех, прежде всего, обращен к подавлению имеющих гауссово распределение — белый шум, гауссово-марковский процесс, узкополосный процесс. В то же время необходимо учитывать, что наибольшую эффективность компенсации гауссово-марковского процесса можно достичь при различии в ширине полосы сигнала и помехи.
Рассмотрим ситуацию, когда на фоне гауссова широкополосного шума с
дисперсией 
действует гауссово-марковский процесс с
дисперсией 
и относительной[1]
шириной полосы α. Корреляционную матрицу входного сигнала можно записать:
где 
;
h= /— отношение мощности полезного сигнала к
мощности шума; N — число весовых коэффициентов
фильтра.
Введем корреляционную матрицу полезного сигнала:
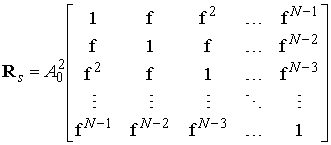(10)
и обратим ее как теплицеву матрицу:
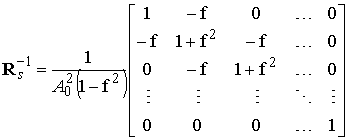. (11)
Запишем равенство из (1), умножим левую и правую части на обратную корреляционную матрицу полезного сигнала:
(12)
(13)
Векторно-матричное умножение в правой части равенства дает единичный вектор:
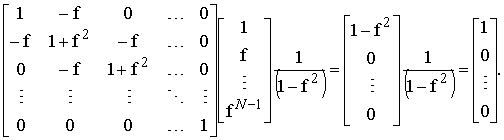(14)
Результатом матричного умножения в левой части является трехдиагональная матрица:
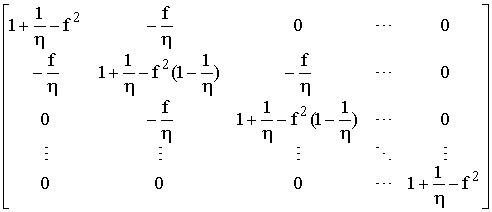, (15)
поэтому равенство можно рассматривать как одну из возможных форм представления однородного разностного уравнения второго порядка для последовательности w0, w1, …, wN–1 [2]:
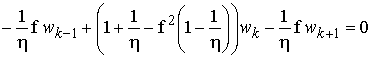, (16)
где k=1,2,…,N–2, с граничными условиями:
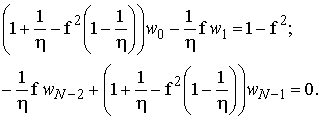(17)
Решение данного разностного уравнения имеет вид [2]:
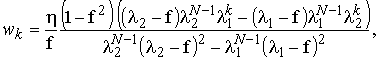(18)
где 
,
Тогда дисперсия ошибки фильтрации на выходе векторно-матричного компенсатора при идеальном опорном канале равна:
Минимальная дисперсия ошибки при бесконечном числе весовых коэффициентов фильтра N находится в пределе и стремится к неустранимой ошибке фильтра Винера:
График зависимости нормированной (к мощности полезного сигнала) дисперсии ошибки фильтрации на выходе векторно-матричного компенсатора от размерности фильтра приведен на рис. 2. С увеличением размерности ошибка уменьшается и стремится к неустранимой ошибке фильтра Винера (20). При этом, чем шире полоса полезного сигнала, тем меньше требуется весовых коэффициентов фильтра.
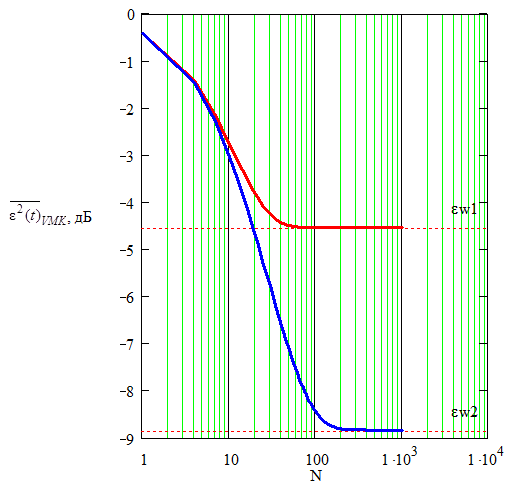
Рис. 2. Зависимость нормированной дисперсии
ошибки фильтрации на выходе
векторно-матричного компенсатора от размерности
фильтра N при разных
значениях ширины полосы гауссово-марковского процесса
α = 0.01 (красная сплошная) и α = 0.001 (синяя сплошная)
Таким образом, эффективность работы компенсатора существенным образом зависит от числа весовых коэффициентов фильтра, однако существует граница, преодоление которой гарантирует достижение минимальной дисперсии ошибки фильтрации (см. рис. 2). Например, для α = 0.01 эта граница составляет 60 весовых коэффициентов, для α = 0.001 — 2000 весовых коэффициентов.
Если на фоне гауссова белого шума действует импульсный полезный
сигнал (например, случайный телеграфный сигнал) с нормированной корреляционной
функцией 
, то корреляционная матрица может быть
представлена аналогично выражению (9), заменив в ней функцию 
на 
, в которой λП
есть интенсивность смены знака (смысл аналогичен процессу Пуассона).
Тогда зависимость нормированной дисперсии ошибки фильтрации на выходе векторно-матричного компенсатора от размерности фильтра N будет повторять график на рис. 2. при λП = α/2.
Когда параметры помех в обоих каналах различаются, например, по дисперсии, взаимнокорреляционный вектор Р’ равен:
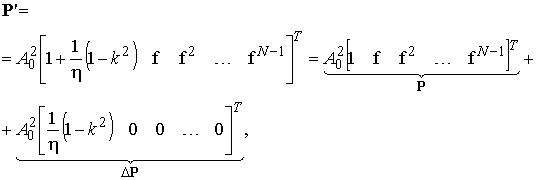(21)
где k2 — коэффициент, определяющий неравенство СКО помех в каналах.
Запишем вектор весовых коэффициентов фильтра с учетом (21):
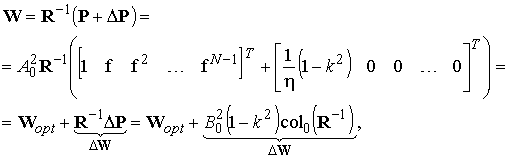(22)
где col0(R-1) — нулевой вектор-столбец обратной корреляционной матрицы входного сигнала.
Второе слагаемое в выражении (22) определяет отклонение ΔW вектора весовых коэффициентов от своего оптимального значения при различии СКО помех в каналах.
Дисперсия ошибки фильтрации на выходе фильтра в векторно-матричной форме в общем виде равна [1]:
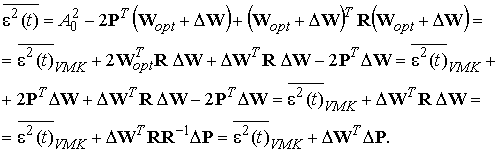(23)
Тогда с учетом (21) и (22) дисперсию ошибки фильтрации можно представить:
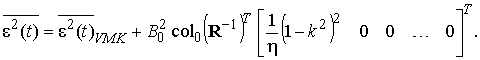(24)
Примем допущение η→0, тогда обратная корреляционная
матрица входного сигнала (9) вырождается в единичную с множителем 1/ и выражение (24) принимает вид:
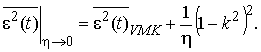(25)
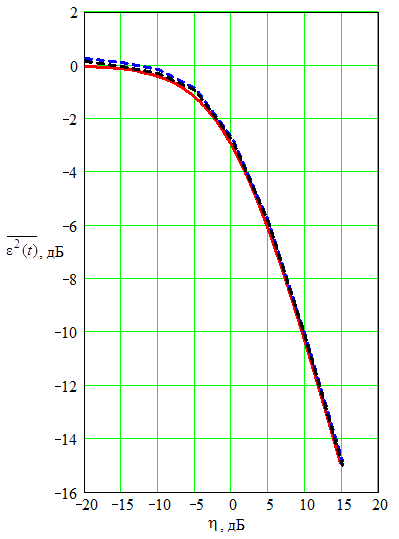
График зависимости нормированной дисперсии ошибки фильтрации на выходе векторно-матричного компенсатора от коэффициента неравенства СКО помех в каналах изображен на рис. 3. В пределе, когда опорный канал отсутствует (k = 0), ошибка стремится к величине, равной сумме дисперсии ошибки фильтрации на выходе векторно-матричного компенсатора (при идеальном опорном канале) и значения обратного отношения мощности сигнал–помеха на входе компенсатора.
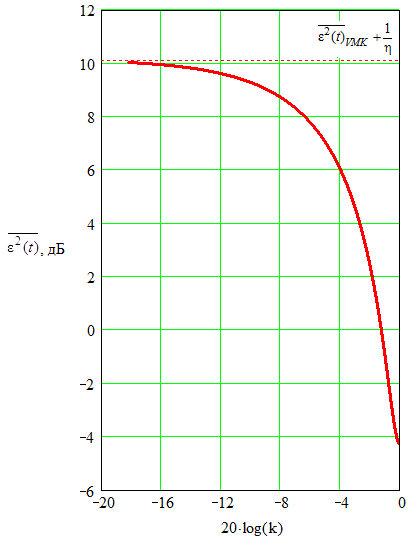
Рис. 3. Зависимость
нормированной дисперсии ошибки фильтрации на выходе
векторно-матричного
компенсатора от коэффициента неравенства
СКО помех в каналах при N=32, η = –10дБ, α = 0.01
Моделирование работы векторно-матричного компенсатора проведено в соответствии со структурной схемой на рис. 4 и алгоритмом на рис. 5 в пакете Simulink.
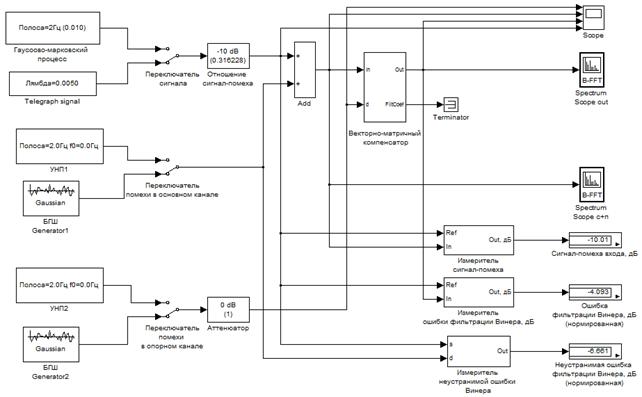
Рис. 4. Схема компьютерного моделирования в Simulink
векторно-матричного
компенсатора непрерывных помех
при выделении гауссово-марковского или
импульсного процессов
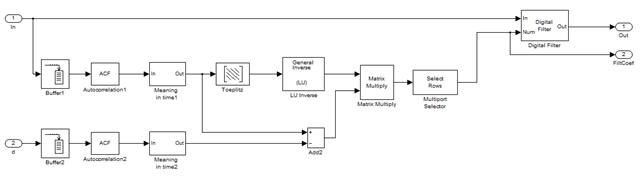
Рис. 5. Алгоритм векторно-матричной компенсации помех, реализованный в пакете Simulink
В таблице 1 и на рис. 6, 7 отображены результаты моделирования работы векторно-матричного компенсатора при выделении гауссово-марковского процесса и симметричного телеграфного процесса на фоне белого гауссова шума (БГШ). При этом в опорном канале действует помеха, некоррелированная с помехой в основном канале, но совпадающая по автокорреляционной функции.
Таблица 1. Зависимость
нормированной дисперсии ошибки фильтрации 
от числа весовых коэффициентов
фильтра при выделении гауссово-марковского
и симметричного телеграфного
процессов на фоне БГШ и η = –10 дБ
|
N |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
|
|
|
Гауссово-марковский процесс (α=0.01) |
–0.8 |
–1.4 |
–2.4 |
–3.5 |
–4.2 |
–4.3 |
–4.3 |
— |
|
Телеграфный процесс (λП = 0.005) |
–0.8 |
–1.4 |
–2.3 |
–3.4 |
–4.1 |
–4.3 |
–4.3 |
–4.3 |
|
|
Гауссово-марковский процесс (α=0.001) |
–0.7 |
–1.3 |
–2.2 |
–3.6 |
–5.3 |
–6.7 |
–7.3 |
— |
|
|
Телеграфный процесс (λП=0.0005) |
–0.8 |
–1.4 |
–2.4 |
–3.9 |
–5.6 |
–6.9 |
–8.1 |
–8.4 |
|
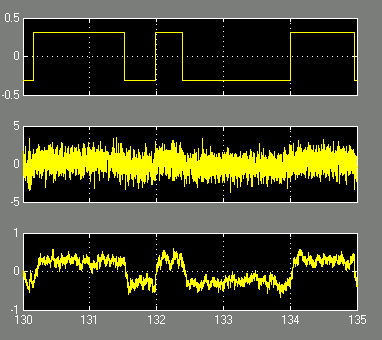
Рис. 6. Эпюры симметричного телеграфного процесса с λП
= 0.0005 (вверху),
его смеси с БГШ (посредине),
выходного сигнала компенсатора (внизу) при N=256
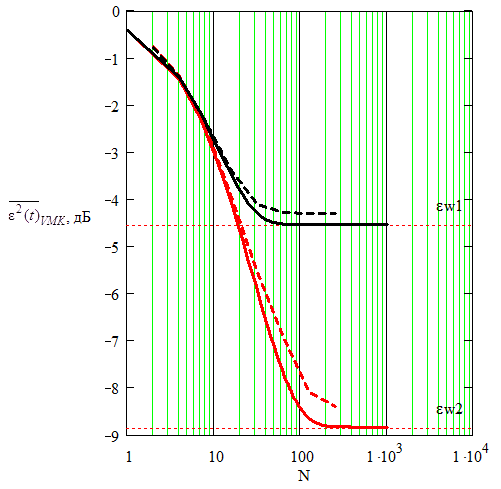
Рис. 7. Зависимость нормированной
дисперсии ошибки фильтрации на выходе
векторно-матричного компенсатора от
размерности фильтра N
при
разных значениях интенсивности симметричного телеграфного процесса
λП = 0.005
(черная сплошная — теоретическая, черная пунктирная — моделируемая)
и λП
= 0.0005 (красная сплошная — теоретическая, красная пунктирная —
моделируемая); η = –10 дБ
В таблице 2 и на рис. 8 — результаты моделирования при неравенстве мощностей и взаимной некоррелированности помех в каналах векторно-матричного компенсатора.
Таблица 2. Зависимость
дисперсии ошибки фильтрации от коэффициента
неравенства СКО
помех в каналах при выделении симметричного телеграфного
процесса
с разными интенсивностями λП на фоне БГШ, η = –10
дБ, N=32
|
k, дБ |
0 |
–0.1 |
–0.2 |
–0.3 |
–0.4 |
–0.5 |
–0.6 |
–0.7 |
|
|
|
λП = 0.05 |
–1.5 |
–1.4 |
–1.4 |
–1.2 |
–1.0 |
–0.8 |
–0.5 |
–0.3 |
|
λП = 0.005 |
–4.1 |
–4.0 |
–3.9 |
–3.6 |
–3.3 |
–2.9 |
–2.6 |
–2.1 |
|
|
λП = 0.0005 |
–5.6 |
–5.5 |
–5.2 |
–4.9 |
–4.5 |
–4.0 |
–3.5 |
–3.0 |
|
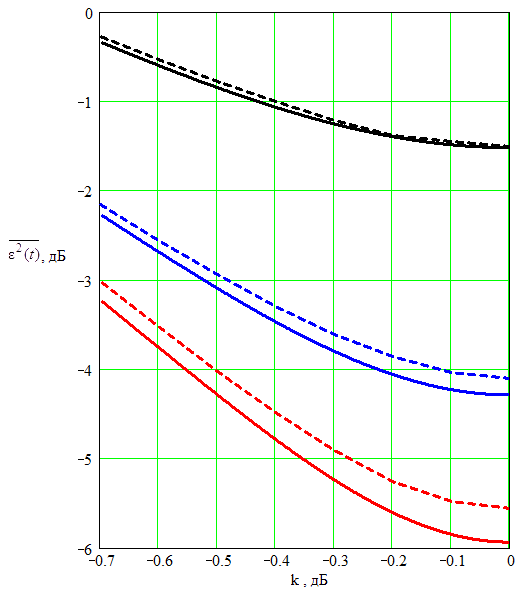
Рис.
8. Зависимость нормированной дисперсии ошибки фильтрации
на выходе
векторно-матричного компенсатора от коэффициента неравенства СКО
помех в
каналах при разных значениях интенсивности симметричного телеграфного процесса
λП = 0.05 (черная сплошная —
теоретическая, пунктирная — моделируемая),
λП = 0.005 (синяя сплошная — теоретическая, пунктирная
— моделируемая) и
λП = 0.0005
(красная сплошная — теоретическая, пунктирная — моделируемая); N=32, η = –10 дБ
Анализ результатов в таблицах 1 и 2 и рисунков 6–8 позволяет сделать следующие утверждения.
Во-первых, векторно-матричный компенсатор работоспособен при выделении непрерывного и импульсного процессов на фоне белого гауссова шума.
Во-вторых, математические расчеты дисперсии ошибки фильтрации гауссово-марковского и симметричного телеграфного процессов при идеальном опорном канале отличаются от результатов моделирования не более чем на 0.5 дБ, что является приемлемыми и доказывает адекватность теоретического выражения. При этом формулы (19) и (20) справедливы для обоих случайных процессов.
В-третьих, коэффициент неравенства СКО по-разному влияет на дисперсию ошибки фильтрации в зависимости от интенсивности — чем меньше λП, тем чувствительнее дисбаланс уровней мощностей в каналах. Кроме того, отличие зависимости дисперсии ошибки фильтрации от коэффициента неравенства СКО помех при введенных допущениях от результатов моделирования составляет не более 0.5 дБ, если интенсивность λП — не менее 0.0005 (при заданном η = –10 дБ). При дальнейшем уменьшении интенсивности телеграфного процесса приближение корреляционной матрицы R к единичной становится более грубым и приводит к увеличению погрешности математических расчетов.
Компенсация сигналоподобных помех
Сигналоподобными помехами будем считать те, которые совпадают или
близки по спектральной плотности с полезным сигналом. Рассмотрим в качестве
помехи гауссово-марковский процесс с дисперсией и
шириной полосы β. Пусть векторно-матричный компенсатор с двумя весовыми
коэффициентами выделяет гауссово-марковский процесс с относительной шириной
полосы α на фоне указанной сигналоподобной помехи.
Дисперсия ошибки фильтрации на выходе компенсатора выражается:
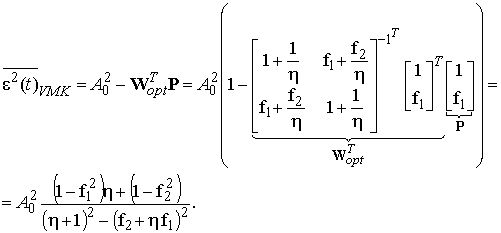(26)
где 
, 
.
Зависимость нормированной к дисперсии
ошибки (26) от ширины полосы помехи показана на рис. 9.
Таким образом, максимальная дисперсия ошибки фильтрации достигается при равенстве полос сигнала и помехи (α=β) и находится из выражения (26):
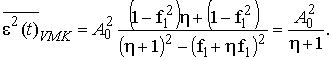(27)
Анализируя формулу (27), можно сделать вывод, что эффективность работы векторно-матричного компенсатора сигналоподобных по спектральной плотности помех не зависит от размерности фильтра, а только от соотношения мощности сигнал-помеха на входе — чем оно больше, тем меньше дисперсия ошибки фильтрации.
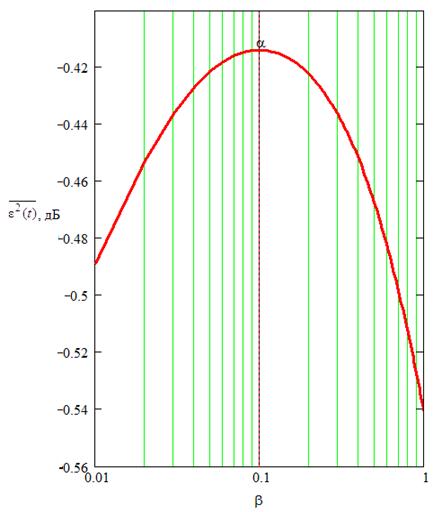
Рис. 9. Зависимость нормированной дисперсии ошибки фильтрации
на
выходе векторно-матричного компенсатора (красная)
от ширины полосы помехи
b при α = 0.1; N=2
Результаты моделирования векторно-матричного компенсатора сигналоподобных помех отображены в таблице 3 и рис. 10. Моделирование проведено в пакете Simulink (рис. 4; переключатель помехи в основном и опорном каналах — в верхнее положение).
Значения таблицы 3 и рис. 10 демонстрируют, что математический расчет дисперсии ошибки фильтрации симметричного телеграфного процесса на фоне сигналоподобной помехи полностью совпал с результатами моделирования.
Таблица
3. Зависимость нормированной
дисперсии ошибки фильтрации
от отношения мощности
сигнал–помеха на входе компенсатора
при выделении
симметричного телеграфного процесса с разными интенсивностями λП
на фоне сигналоподобной гауссово-марковской помехи (N=32)
|
η, дБ |
–20 |
–15 |
–10 |
–5 |
0 |
5 |
10 |
15 |
|
|
|
λП = 0.05 b = 0.1 |
0.0 |
–0.1 |
–0.4 |
–1.1 |
–3.0 |
–6.1 |
–10.4 |
–15.1 |
|
λП = 0.005 b = 0.01 |
0.0 |
–0.1 |
–0.4 |
–1.0 |
–2.9 |
–6.0 |
–10.3 |
–15.1 |
|
Рис. 10. Зависимость
нормированной дисперсии ошибки фильтрации
на выходе векторно-матричного
компенсатора (красная сплошная — теоретическая)
от отношения мощности
сигнал–помеха на входе компенсатора при разных значениях
интенсивности
симметричного телеграфного процесса
λП = 0.05 (черная
пунктирная — моделируемая),
λП = 0.005 (синяя пунктирная —
моделируемая)
на фоне сигналоподобной гауссово-марковской помехи; N=32
Под импульсными помехами будем понимать случайный процесс, представляющий собой последовательность одиночных импульсов, параметры которых представляют случайные величины. Импульсная помеха, чаще всего, это хаотическая последовательность импульсов со случайной длительностью, амплитудой и временем появления. Однако для упрощения представления импульсной помехи можно ограничиться случайным временем появления фронтов (скачков уровней), а амплитуду установить детерминированной. Такими свойствами обладает ограниченный по амплитуде телеграфный процесс, у которого вероятность скачков уровня описывается плотностью распределения вероятности Пуассона с интенсивностью λП. Его спектральная плотность мощности описывается выражением:
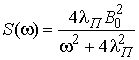. (28)
При интенсивности, стремящейся к бесконечности, характеристики телеграфного процесса стремятся к характеристикам белого гауссова шума. Если в качестве полезного сигнала взять гауссово-марковский процесс или телеграфный процесс с интенсивностью λП << 1, а импульсной помехой представить телеграфный сигнал высокой интенсивности (λП = 1), то расчет дисперсии ошибки фильтрации на выходе векторно-матричного компенсатора можно производить по (19).
Результаты моделирования работы векторно-матричного компенсатора импульсных помех отображены в таблицах 4, 5 и на рис. 12 и 13. Моделирование проведено в пакете Simulink (рис. 11).
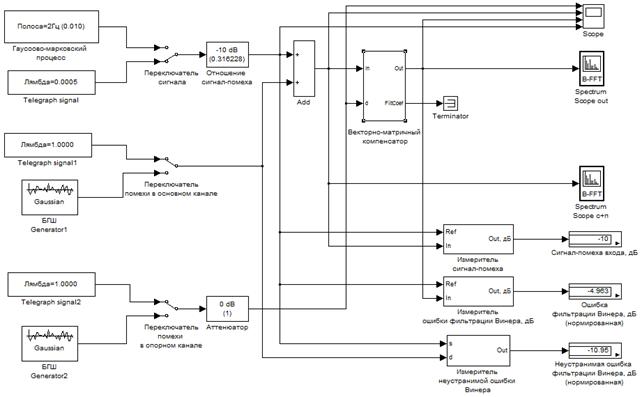
Рис. 11. Схема компьютерного моделирования в Simulink векторно-матричного
компенсатора импульсных помех при
выделении импульсного процесса
Таблица 4. Зависимость нормированной дисперсии
ошибки фильтрации
от числа весовых коэффициентов
фильтра при выделении симметричного телеграфного сигнала
с разными
интенсивностями λП на фоне симметричного телеграфного процесса
высокой интенсивности
(λП=1) и η = –10 дБ
|
N |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
|
|
|
λП=0.005 |
–0.6 |
–1.0 |
–1.9 |
–2.9 |
–3.7 |
–4.0 |
–4.1 |
–4.1 |
|
λП=0.0005 |
–0.5 |
–1.0 |
–1.9 |
–3.3 |
–5.0 |
–6.6 |
–7.6 |
–7.9 |
|
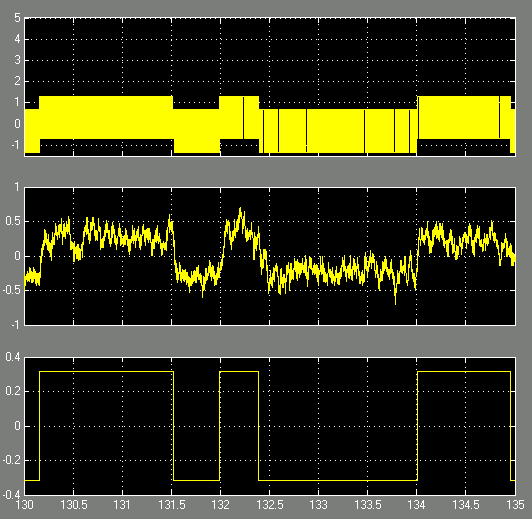
Рис. 12. Эпюры симметричного телеграфного процесса с λП
=0.0005 (внизу),
его смеси с симметричным телеграфным процессом высокой
интенсивности (λП=1) (вверху),
выходного сигнала компенсатора
(посредине) при N=256
Таблица
5. Зависимость
нормированной дисперсии ошибки фильтрации
от
отношения мощности сигнал-помеха на входе компенсатора при выделении
симметричного
телеграфного сигнала с разными интенсивностями λП
на фоне
симметричного
телеграфного процесса высокой интенсивности (λП=1) и N=32
|
η, дБ |
–20 |
–15 |
–10 |
–5 |
0 |
5 |
10 |
15 |
|
|
|
λП = 0.005 |
–0.5 |
–1.8 |
–3.7 |
–6.0 |
–8.3 |
–10.8 |
–13.6 |
–16.9 |
|
λП = 0.0005 |
–0.5 |
–2.2 |
–5.0 |
–8.6 |
–12.0 |
–14.8 |
–17.4 |
–20.0 |
|
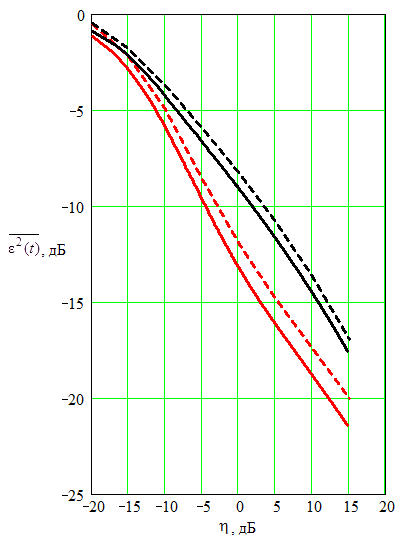
Рис. 13. Зависимость нормированной дисперсии ошибки фильтрации
на
выходе векторно-матричного компенсатора (сплошная — теоретическая;
пунктирная — моделируемая)
от отношения мощности сигнал–помеха на входе
компенсатора при разных значениях
интенсивности симметричного телеграфного сигнала
λП =0.005 (черная),
λП =0.0005 (красная)
на фоне симметричного телеграфного процесса высокой интенсивности (λП=1);
N=32
Сравнение данных из таблицы 4 с графиком теоретической зависимости дисперсии ошибки фильтрации на рис. 2 (при подстановке α = 2λП), а также изображенная на рис. 13 зависимость нормированной дисперсии ошибки фильтрации на выходе векторно-матричного компенсатора показывает, что отклонение результатов моделирования от теории составляет не более 1 дБ, и подтверждает правильность применения (19) при расчете дисперсии для данного случая.
1. Синтезирован векторно-матричный компенсатор помех, который работоспособен при выделении непрерывного и импульсного процессов на фоне белого гауссова шума или импульсной помехи при полной взаимной некоррелированности помех в каналах компенсации.
2. Математические расчеты дисперсии ошибки фильтрации гауссово-марковского и симметричного телеграфного процессов при идеальном опорном канале отличаются от результатов моделирования не более чем на 1 дБ, что доказывает адекватность теоретических выкладок.
3. Коэффициент неравенства СКО по-разному влияет на дисперсию ошибки фильтрации в зависимости от интенсивности импульсного сигнала — чем меньше λП, тем чувствительнее дисбаланс уровней мощностей в каналах.
4. Эффективность работы векторно-матричного компенсатора сигналоподобных по спектру помех зависит только от соотношения мощности сигнал-помеха на входе — чем оно больше, тем меньше дисперсия ошибки фильтрации.
5. При компенсации белого гауссова шума или импульсной помехи выигрыш в отношении сигнал–помеха на выходе векторно-матричного компенсатора может достигать около 18 дБ (при h = –10дБ; N=256).
Литература
1. Уидроу Б., Стирнз С. Адаптивная обработка сигналов : пер. с англ. – М. : Радио и связь, 1989. – 440 с.
2. Шахтарин Б.И. Фильтры Винера и Калмана. – М : Гелиос АРВ, 2008. 408с. : ил.