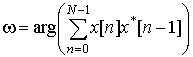УДК 621.396.96
УСОВЕРШЕНСТВОВАННЫЙ
АЛГОРИТМ ОЦЕНКИ ЧАСТОТЫ НА ОСНОВЕ ИТЕРАЦИОННОГО ВЫЧИСЛЕНИЯ
АВТОКОРРЕЛЯЦИОННОЙ ПОСЛЕДОВАТЕЛЬНОСТИ
В. Г. Волков 1 , Ю. Н. Кривов 1, И. В. Лукьянов 2
1 ООО «НПП «ЛАМА», г. Рыбинск
2 ФГБОУ ВПО «Рыбинский государственный авиационный технический университет имени П. А. Соловьева»
Статья поступила в редакцию 3 октября 2016 г.
Аннотация. Одной из важных задач при обработке радиосигналов является оценка несущей частоты. В статье проводится краткий обзор статистически эффективных методов оценки частоты. Эти методы оказываются недостаточно вычислительно эффективными для задач критичных к времени выполнения. По этой причине на практике применяют различные способы комплексирования. Это обеспечивает достижение приемлемых для практических приложений результатов. Одним из таких способов является комплексирование процедуры итерационного вычисления автокорреляционной последовательности, которая обеспечивает увеличение отношения сигнал шум, и авторегрессионной оценки частоты.
В статье рассматрен усовершенствованный алгоритм оценки частоты на основе итерационного вычисления автокорреляционной последовательности. Предложенный алгоритм требует почти в два раза меньше операций сложения и умножения. Такой результат достигается за счет отказа от обратного преобразования Фурье и отказа от решения уравнения Юла-Уолкера. Для оценки частоты используется первый член автокорреляционной последовательности. Для его вычисления используется алгоритм Герцеля. Сформулировано правило корректного выбора длины блоков нулей, которыми дополняется исходная выборка.
Приводятся результаты математического моделирования. Проводится сравнение среднеквадратической ошибки оценки частоты с границей Крамера-Рао. Показано, что рассмотренный алгоритм обеспечивает статистически эффективную оценку частоты при отношении сигнал/шум от минус 3 до 50 дБ. Такой результат достигается при использовании трех итераций и размере выборки в 64 отсчета. Полученные эмпирические кривые могут быть использованы для оптимального выбора параметров рассмотренного метода для практических приложений.
Ключевые слова: оценка частоты, эффективные оценки, автокорреляционная последовательность.
Abstract. One of the important problems in radio signals processing is the carrier frequency estimation. A review of known statistically efficient methods of frequency estimation is presented. These methods are not computationally efficient for critical to real-time tasks. For this reason, in practice, different methods of complexing are used. This provides acceptable results in practical applications. One of such methods is combining of the iterative procedure of autocorrelation sequence calculation (which provides an increase in the signal to noise ratio) and AR-frequency estimation.
This article presents an improved frequency estimation algorithm based on the iterative calculation of the autocorrelation sequence. The proposed algorithm requires nearly half operations of addition and multiplication. This is achieved by eliminating the inverse fast Fourier transform and the solution of the Yule-Walker equation. First term of autocorrelation sequence is used for frequency estimation. Goertzel algorithm is used for term calculation. A correct length selection rule for zero blocks which fill original signal, has been formulated.
The results of the simulation algorithm are provided. A comparison of the mean square error with the Cramer-Rao bounds is provided. It is shown that analyzed algorithm provides a statistically efficient frequency estimation for a signal/noise ratio from –3 to 50 dB. This result is achieved by using three iterations and 64 samples number. Obtained empirical curves can be used for optimal selection of parameters of discussed method for practical applications.
Keywords: frequency estimation, efficient estimator, autocorrelation sequence.
Введение
Одной из важных задач при обработке радиосигналов является оценка несущей частоты. Для этого существует множество методов, например, рассмотренных в работах [1–12]. Наиболее интересными представляются так называемые статистически эффективные методы, т.е. такие методы, которые при заданной модели сигнала и шума дают оценку неизвестного параметра, достигающую некоторой теоретической границы. Для сигналов в канале с аддитивным белым гауссовским шумом (АБГШ) эффективной считают оценку, дисперсия которой достигает границы Крамера-Рао (ГКР) [13].
Эффективные оценки частоты
Известно, что максимально правдоподобная оценка (МП-оценка) частоты, являющаяся эффективной оценкой, может быть получена по периодограмме сигнала [4,5]
, (1)
где 
–
МП-оценка частоты;
–
периодограмма сигнала.
Вычисление МП-оценок по (1) связано с существенными вычислительными затратами, поскольку для этого требуется построение периодограмм с малым частотным шагом с помощью процедуры дискретного преобразования Фурье (ДПФ) на неортогональной частотной сетке.
Для получения оценок частоты существуют и более "лёгкие" с вычислительной точки зрения методы, которые основаны на аппроксимации периодограммы некоторой аналитической функцией и последующим поиском ее максимума [12]. Иногда такие оценки оказываются близкими к МП, однако для коротких выборок сигналов они могут оказаться смещенными. Это связано с тем, что такая практика оказывается эффективной только тогда, когда большая часть энергии сигнала сосредоточена в пределах одного спектрального отсчета [14].
Другим способом получения статистически эффективных оценок является применение параметрических методов. Запишем модель комплексной экспоненты в присутствии АБГШ
,
где 
– комплексная амплитуда
сигнала;
–
амплитуда сигнала;
–
начальная фаза сигнала;
– частота;
– номер отсчета;
– начальная фаза;
– АБГШ.
Эффективная оценка неизвестных параметров сигнала может быть найдена путем решения экстремальной задачи по минимизации квадратической функции потерь
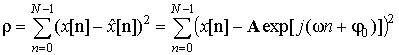
где 
–
наблюдаемый отсчет сигнала.
Для этого решают систему уравнений вида
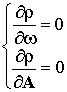
В [1] показано, что аналитические решения этой системы отсутствуют. Эта система может быть решена только с помощью численных методов оптимизации, требующих существенных вычислительных затрат.
Таким образом, известные эффективные оценки частоты оказываются недостаточно вычислительно эффективными для задач критичных к времени выполнения (например, в системах реального времени). По этой причине достаточно часто используют оценки близкие к статистически эффективным, а так же различные способы комплексирования, обеспечивающие достижение приемлемых для практических приложений результатов.
В [6] предлагается ряд быстрых параметрических оценок. Так авторегрессионная оценка (АР-оценка) вида
оказывается быстрой, однако является статистически неэффективной, поскольку не достигает границы Крамера-Рао [6]. Тем не менее, эта оценка может оказаться приемлемой в ряде прикладных задач для сигналов с высоким отношением сигнал/шум (ОСШ).
Алгоритм оценки частоты на основе итерационного вычисления автокорреляционной последовательности
В работах [15, 16] предлагается интересный с точки зрения практического применения способ комплексирования при оценке частоты. Данный способ основан на увеличения ОСШ сигналов с помощью процедуры итерационного вычисления оценки автокорреляционной последовательности (АКП) [17]. В работе [15] рассмотрена вычислительно эффективная реализация итерационного вычисления АКП, основанная на однозначной связи дискретной свертки с дискретным преобразования Фурье. В работе [15] итерационное вычисление АКП является предварительным этапом при оценке частоты действительных гармонических сигналов с помощью АР-оценки второго порядка. При этом в [15] сначала вычисляется АКП, после чего по оценке АКП составляется 2x2 автокорреляционная матрица и решается уравнение Юла-Уолкера. Схема работы этого алгоритма представлена на рисунке 1.
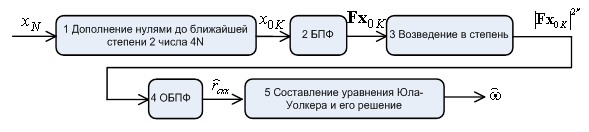
Рисунок 1 –
Алгоритм оценки частоты на основе
итерационного вычисления АКП
Усовершенствованный алгоритм оценки частоты на основе итерационного вычисления АКП
Уменьшение операций сложения и умножения
Обобщив алгоритм, представленный в [15], на комплексные сигналы и приняв во внимание, что оценка АКП уже содержит оценку АР-параметра первого порядка, этот алгоритм можно значительно усовершенствовать, избавившись от избыточной процедуры вычисления обратного преобразования Фурье, составления и решения уравнения Юла-Уолкера.
Действительно оценка АКП определяется выражением [1]
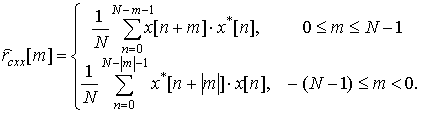(3)
По (2) и (3) оценку частоты можно получить как
, (4)
где arg – функция взятия аргумента комплексного числа.
Поскольку множитель N в выражении (4) определяет только значение модуля комплексного числа, им можно пренебречь и оценку частоты определить как
(5)
Для получения оценки согласно (5) необходим только один член АКП. В связи с этим вычисление обратного быстрого преобразования Фурье (ОБПФ) становится избыточным. Искомая оценка может быть определена с помощью обратного дискретного преобразования Фурье (ОДПФ)
,
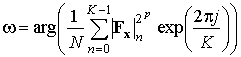где 
–
БПФ исходного сигнала (в
обозначениях автора [15]);
p – число итераций для вычисления АКП;
K – число спектральных отсчетов после дополнения нулями.
Число операций умножения при вычислении ОДПФ можно сократить, воспользовавшись алгоритмом Герцеля [18]. Тогда оценка частоты может быть получена по формуле
,
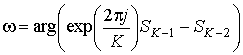(6)
где 
, для n = 0, 1, …, K–1;
.
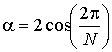В таблице 1 приводится сравнение усовершенствованного и исходного алгоритмов по количеству умножений и сложений.
В таблице 2 представлено общее количество умножений и сложений для различных значений K и числа итераций p вычисления АКП.
Таблица 1 – Сравнение вычислительной сложности исходного и усовершенствованного алгоритмов оценки частоты
|
Параметр |
Исходный алгоритм |
Усовершенствованный алгоритм |
|
Действительных умножений: БПФ вычисление модуля возведение в степень ОБПФ Алгоритм Герцеля Оценка АР-параметра Общее |
2K Kp
– 5
|
2K Kp – K + 4 –
|
|
Действительных сложений: БПФ вычисление модуля ОБПФ Алгоритм Герцеля Оценка АР-параметра Общее |
K
– 1
|
K – 2K + 1 –
|
Таблица 2 – Число умножений и сложений исходного и усовершенствованного алгоритмов оценки частоты
|
K |
p |
Исходный алгоритм |
Усовершенствованный алгоритм |
||
|
умножений |
сложений |
умножений |
сложений |
||
|
32 |
3 |
1445 |
1313 |
836 |
737 |
|
64 |
3397 |
3137 |
1924 |
1729 |
|
|
128 |
7813 |
7297 |
4356 |
3969 |
|
|
256 |
17669 |
16641 |
9732 |
8961 |
|
|
512 |
39429 |
37377 |
21508 |
19969 |
|
|
1024 |
87045 |
82945 |
47108 |
44033 |
|
|
32 |
4 |
1477 |
1313 |
868 |
737 |
|
64 |
3461 |
3137 |
1988 |
1729 |
|
|
128 |
7941 |
7297 |
4484 |
3969 |
|
|
256 |
17925 |
16641 |
9988 |
8961 |
|
|
512 |
39941 |
37377 |
22020 |
19969 |
|
|
1024 |
90112 |
86014 |
48132 |
44033 |
|
По таблицам 1 и 2 видно, что усовершенствованный алгоритм обеспечивает снижение вычислительных затрат практически в два раза.
Правило выбора длины блока нулей
В работе [15] отмечается, что погрешность оценки частоты зависит от длины блока нулей, которыми дополняется исходная выборка данных. В этой же работе эмпирическим путем устанавливается оптимальная длина блока нулей равная 3N. Однако это утверждение является неточным, поскольку, исходя из связи оценки АКП и БПФ, для корректного итерационного вычисления оценки АКП длина блока нулей должна зависеть от количества итераций вычисления АКП. Необходимо отметить, что эта неточность не проявляет себя в диапазонах ОСШ, исследуемых в [15] (от минус 30 до минус 5), поэтому в таких условиях допустимо пользоваться эмпирическим правилом по выбору длины блока нулей. Однако при более высоких ОСШ некорректный выбор длины блоков нулей проявляется в достижении кривых среднеквадратических ошибок оценки частоты области «насыщения», начиная с некоторого значения ОСШ, имеющего определённое значение для каждого N и р (см. рисунок 3). Устранить эту проблему можно, описав явную зависимость длины блока нулей от числа итераций вычисления АКП.
В действительности, оценка АКП определяется соотношением
,
где 
– оператор
ОБПФ;
– оператор
БПФ.
При этом в соответствии с алгоритмом быстрого вычисления АКП исходная выборка x длинной N дополняется нулями до K = 2N, т. е. оценка АКП имеет размерность 2N. Для выполнения второй итерации вычисления АКП необходимо выполнить следующее преобразование
при этом оценка АКП дополняется
нулями до K2 = 2K = 4N. Таким образом, на p итерации
имеем результирующую выборку размерностью 
.
С учетом проведенных усовершенствований, алгоритм можно представить в виде схемы (рисунок 2).
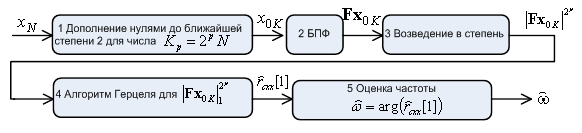
Рисунок 2 – Схема работы усовершенствованного алгоритма оценки частоты на основе итерационного вычисления АКП
Таким образом, усовершенствованный
алгоритм требует 
операций умножения и 
операций сложения.
Экспериментальное исследование алгоритма
Для проверки эффективности усовершенствованного алгоритма был проведен численный эксперимент по определению зависимости среднеквадратической ошибки оценки частоты от ОСШ, полученной при различном числе итераций в процессе вычисления АКП. Эксперимент проводился методом Монте-Карло, а полученные результаты сравнивались с границей Крамера-Рао и АР-оценкой (2). Поскольку модификация исходного алгоритма заключалась в оптимизации числа умножений и сложений, среднеквадратические ошибки оценок усовершенствованного и исходного алгоритма идентичны и их сравнение по точности не проводилось.
В работе [15] отсутствуют результаты моделирования при ОСШ больших 5 дБ, поэтому с целью уточнения характеристик алгоритма в настоящей работе расширен диапазон изменения ОСШ от минус 30 до 50 дБ.
В качестве функции ошибки была выбрана логарифмическая среднеквадратическая ошибка
,
(7)
где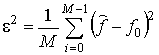 
;
–
оценка нормированной частоты;
–
истинное значение нормированной частоты;
–
число экспериментов для фиксированного ОСШ.
Граница Крамера-Рао в соответствии с [6] определялась по формуле
,
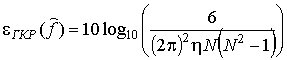(8)
где – отношение
сигнал/шум, выраженное в разах;
– число
отсчетов в сигнале.
Значение истинной нормированной частоты случайным образом выбиралось из диапазона от минус 0,5 до 0,5 для каждого ОСШ. Таким образом, в процессе эксперимента перекрывалась половина частотного диапазона принимаемых сигналов. Из анализа были исключены высокие частоты, поскольку при измерениях стремятся иметь 4 и более отсчётов на периоде. Количество экспериментов для каждого ОСШ составило 10000.
На рисунках 4–10 приведены результаты моделирования для числа отсчетов входного сигнала N кратных степени двух от 64 до 4096. Обозначения, принятые на рисунках: N – число отсчетов в сигнале; АР – оценка, полученная по (2); АКП-АР – оценка с помощью усовершенствованного алгоритма оценки частоты на основе итерационного вычисления АКП, где p – число итераций вычисления АКП; ГКР – граница Крамера-Рао.
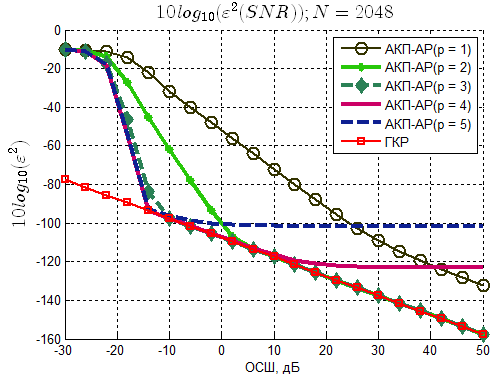
Рисунок 3 – Зависимость среднеквадратической ошибки
оценки частоты сигнала от ОСШ (K = 4N)
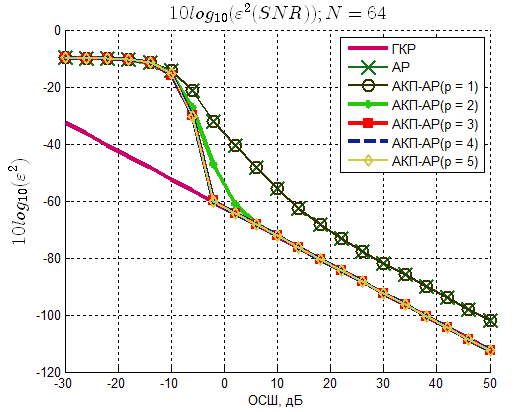
Рисунок 4 – Зависимость среднеквадратической ошибки
оценки частоты сигнала от ОСШ (N=64)
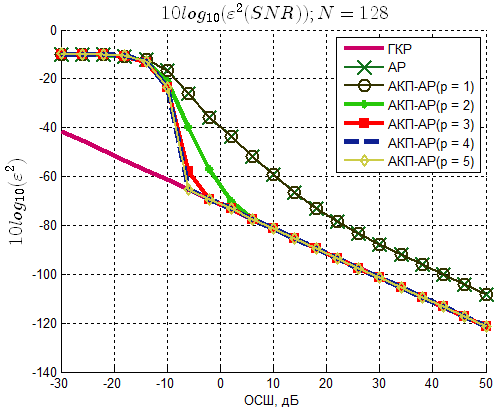
Рисунок 5 – Зависимость среднеквадратической ошибки
оценки частоты сигнала от ОСШ (N=128)
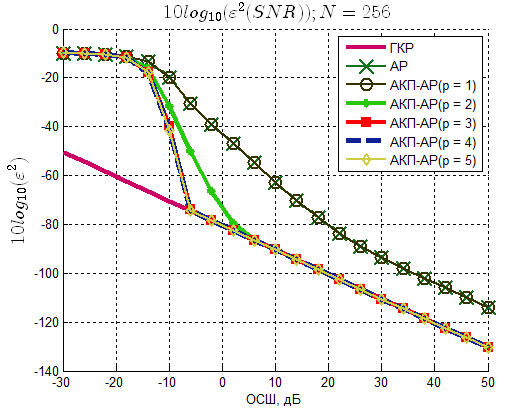
Рисунок 6 – Зависимость среднеквадратической ошибки
оценки частоты сигнала от ОСШ (N=256)
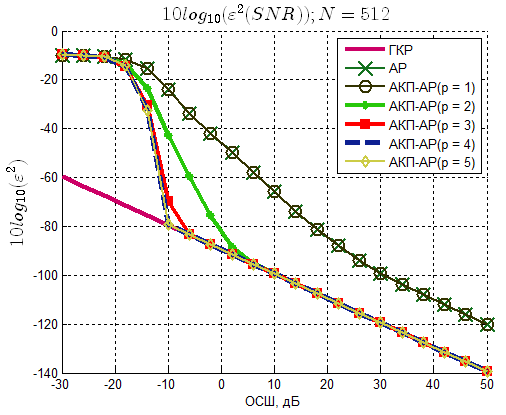
Рисунок 7 – Зависимость среднеквадратической ошибки
оценки частоты сигнала от ОСШ (N=512)
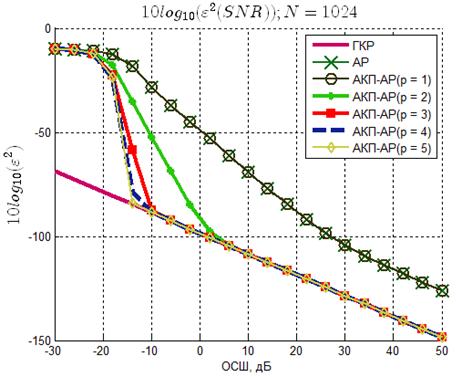
Рисунок 8 – Зависимость среднеквадратической ошибки
оценки частоты сигнала от ОСШ (N=1024)
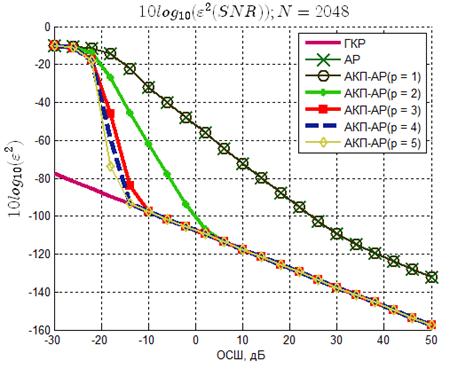
Рисунок 9 – Зависимость среднеквадратической ошибки
оценки частоты сигнала от ОСШ (N=2048)
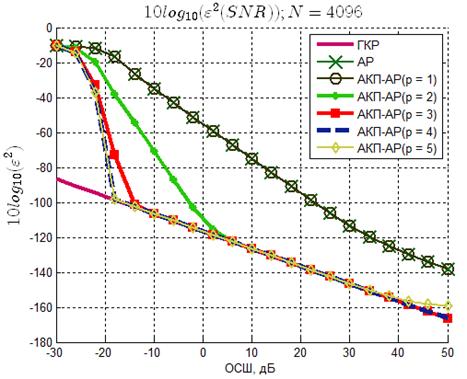
Рисунок 10 – Зависимость среднеквадратической ошибки
оценки частоты сигнала от ОСШ (N=4096)
По полученным результатам моделирования можно сделать следующие выводы:
1. Форма полученных зависимостей, их взаимное расположение и расположение относительно границы Крамера-Рао (ГКР) сохраняют подобие во всем диапазоне использованных N. Следовательно, алгоритм может быть применен для оценки частот в выборках произвольного размера.
2. Оценки с числом итераций вычисления АКП p больше 1 дают статистически эффективную оценку частоты в диапазоне ОСШ, зависящем от числа итераций p и числа отсчетов N. Так метод с p=3 при наихудшем случае дает эффективную оценку в диапазоне ОСШ от минус 3 дБ до 50 дБ. С увеличением p и N область эффективных оценок смещается в сторону уменьшения ОСШ.
3. С уменьшением ОСШ, начиная с определенного значения, эффективность всех оценок резко падает, а кривые достигают области «насыщения». Причем при увеличении числа отсчетов N ширина области «насыщения» уменьшается. Это означает, что с увеличением N эффективность оценок при отрицательных ОСШ становится несколько выше.
4. С увеличением p больше 3 эффективность оценок возрастает незначительно. Использование рассмотренного алгоритма со значением p большим 3-х оправдано только на ограниченном интервале значений ОСШ. Этот интервал для различных N и р имеет своё положение.
Заключение
1. В статье рассмотрен
усовершенствованный быстрый алгоритм оценки частоты, основанный на итерационном
вычислении АКП. Алгоритм требует практически в два раза меньше операций
умножения и сложения, чем исходный, а именно действительных
умножений и действительных сложений.
2. При числе итераций вычисления АКП равном трем алгоритм обеспечивает статистически эффективную оценку частоты в диапазоне ОСШ не меньшем, чем от минус 3 до 50 дБ.
3. Полученные эмпирические кривые могут быть использованы для оптимального выбора параметров рассмотренного метода для практических приложений.
Литература
1. С. Л. Марпл-мл. Цифровой спектральный анализ и его приложения: Пер. с англ. М : Мир, 1990, 604 с., ил.
2. Шахтарин Б. И., Ковригин В. А. Методы спектрального оценивания случайных процессов: Учеб. Пособие. 2-е изд, исправ. – М.: Горячая линия–Телеком, 2011. – 256 с.: ил.
3. Е. В. Дмитриев. Аппроксимация коротких процессов, сигналов, функций и расчет их гармонических дискретных спектров. Физика волновых процессов и радиотехнические системы. Том 10, № 1, 2007 г, стр. 33-46.
4 Rife D. C., Boorstyn R. R. Single-tone parameter estimation from discrete-time observations. IEEE Trans. Inform. Theory, 1974, vol. IT–20, pp. 591–598, Sept.
5. Clarkson V. Efficient single frequency estimators. In Proc. Internat. Sympos. Signal Process., August 1992 Appl., pages 327-330.
6. Kay S. A Fast and Accurate Single Frequency Estimator. IEEE Trans. Acoustics Speech Signal Processing, Dec. 1989, vol. 37, no. 12, pp. 1987–1990.
7. Lank G. W., Reed I. S., and Pollon G. E., A semicoherent detection and doppler estimation statistic. IEEE Transactions on Aerospace and Electronic Systems, Mar. 1973, vol. AES–9, pp. 151–165.
8. Ronkin M., Khrestina E., Kalmikov A. Frequency Estimation for Short Realization of Radar Signals: The New Algorithm Presentation. Contemporary Engineering Sciences, 2014, Vol. 7, №. 33, pp. 1777-1781. [Электронный ресурс] // Hikari Ltd [сайт]. URL: http://www.m-hikari.com/ces/ces2014/ces33-36-2014/khrestinaCES33-36-2014-1.pdf (дата обращения 10.04.2015).
9. Nishiyama K. A Nonlinear Filter for Estimating a Sinusoidal Signal and Its Parameters in White Noise: On the Case of a Single Sinusoid. IEEE Transactions on Signal Processing, 1997, Vol. 45, NO. 4.
10. Butt N. R., Jakobsson A., Mossberg M. Computationally efficient online phase-based frequency estimation of a single tone. 17th European Signal Processing Conference (EUSIPCO 2009) Glasgow, Scotland, August 24-28, 2009
11. Hing Cheung So, Hongqing Liu. Improved Single-Tone Frequency Estimation by Averaging and Weighted Linear Prediction, ETRI Journal, February 2011, vol. 33, № 1,
12. Jacobsen E., Kootsookos P. Fast, Accurate Frequency Estimators.
13. Kay S.M. Fundamentals of Statistical Signal Processing: Estimation Theory (v.1). Prentice Hall, Upper Sadle River, NJ, 1998. 595 p.
14. Ричард Лайонс. Цифровая обработка сигналов: Второе издание. Пер. с англ. М.: Бином-Пресс, 2006, 656 с.:ил.
15. Никифоров А. А. Идентификация и оценка информационных параметров навигационных систем с кодовым разделением. Диссертация на соискание ученой степени кандидата технических наук. Московский государственный технический университет имени н. Э. Баумана, 2014
16. Никифоров А.А. Алгоритм итеративного вычисления автокорреляционной функции в задаче оценки частоты широкополосного сигнала // Механизация строительства. Т. 11. С. 53–55.
17. С. А. Останин. Увеличение отношения сигнал/шум методом последовательного вычисления автокорреляционной функции. «Журнал Радиоэлектроники», №12, 2011. [Электронный ресурс] http://jre.cplire.ru/win/dec11/13/text.html (дата обращения 15.09.2016).
18. Goertzel, G. An Algorithm for the Evaluation of Finite Trigonometric Series. American Mathematical Monthly, 1985 № 65 (1), pp. 34–35.