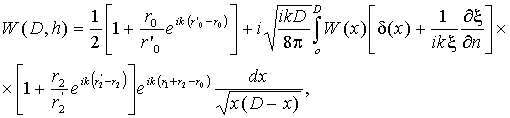УДК 538.566
ОПРЕДЕЛЕНИЕ ФУНКЦИИ ОСЛАБЛЕНИЯ ПОЛЯ ЗЕМНОЙ ВОЛНЫ ПРИ ПРИЕМЕ НА РАЗНЫХ ВЫСОТАХ ПОЛЕТА САМОЛЕТА
М. Г. Дембелов 1, Ю. Б. Башкуев 1, В. П. Мельчинов 2
1 Институт физического материаловедения СО РАН
2 Северо-Восточный федеральный университет им. М.К. Амосова
Статья поступила в редакцию 9 октября 2016 г.
Аннотация. Приведены удобные для численных расчетов формулы, полученные на основе интегрального уравнения Кирхгофа, для расчета функции ослабления поля земной волны с учетом высоты приема сигнала над геометрически и электрически неоднородными радиотрассами. Выполнены сравнительные расчеты функции ослабления по методу интегрального уравнения и по ряду нормальных волн при приеме на разных высотах в диапазоне ДВ. Показано, что измерения напряженности поля на борту самолета при полете на высоте до 200 метров практически не отличаются от измерений на земной поверхности. Дана оценка влияния возмущения в виде геометрической неоднородности в форме Гауссовой горы на процесс распространения радиоволн с учетом разных высот приема на частоте 100 кГц. Выполнены экспериментальные работы на Крайнем Севере в районе п. Черский по измерению поверхностного импеданса и напряженности электромагнитного поля с борта самолета над равнинной трассой Черский-Чокурдах и над гористой трассой Черский-Певек на частоте приводной радиостанции аэропорта 257 кГц. Дана оценка точности расчетов поля земной волны по локальным электрическим характеристикам высокоширотной подстилающей среды с учетом геометрических неоднородностей и высоты приема сигнала. Обработка результатов измерений напряженности электромагнитного поля с борта самолета показала хорошую сходимость с расчетными данными.
Ключевые слова: поле земной волны, функция ослабления, поверхностный импеданс, рельеф местности, высота приема сигнала.
Abstract. Formulas derived from Kirchhoff's integral equation are offered for calculations of an attenuation function of the Earth’s wave field taking into consideration the height of the signals reception for geometrically and electrically inhomogeneous radio paths. Comparative calculations of an attenuation function are carried out by the method of integral equations and on the normal waves row for reception at different heights in the LF range. It is shown that field intensity measurements on a board of the aircraft when flying at an altitude up to 200 meters don’t differ from measurements on the Earth's surface. An estimation of the impact of perturbations in the form of geometric inhomogeneity as Gaussian hill on a process of the radio wave propagation taking into account the different heights of the reception at the 100 kHz frequency is given. Experimental works in the far North region near Chersky town were carried out. Measurements of the surface impedance and the electromagnetic field intensity from the aircraft above a flat radio path Chersky-Chokurdakh, and over a mountainous radio path Chersky-Pevek at the frequency of 257 kHz that is the airport homing station were carried out. The estimation of accuracy of calculations of the field of the Earth’s wave by the local electrical characteristics of underlying high-latitude media taking into account geometric inhomogeneities and the height of the receiving signal is given. The processing of measurement results of electromagnetic field intensity from the aircraft showed a good correlation with the calculated data.
Key words: Earth’s wave field, an attenuation function, surface impedance, terrain relief, height of signal reception.
Введение
Практический интерес к исследованиям распространения радиоволн с учетом высоты приема сигналов вызван требованиями обеспечения качества работы радиотехнических систем навигации, пеленгации и управления воздушным движением, особенно в высоких широтах. Также существенный интерес к процессам возбуждения и распространения ДВ-СВ радиоволн в высоких широтах представляют задачи передачи дифференциальных поправок навигационных спутниковых систем с использованием СВ-радиомаяков (283-325 кГц) с радиусом рабочей зоны действия до 500 км. Такие радиомаяки уже широко используются на северных реках, на Арктическом побережье, а также в акватории Северного ледовитого океана. Значимость исследований возрастает в связи с освоением природных ресурсов Северного Ледовитого океана и проведением ледовой разведки Северного морского пути с использованием летательных аппаратов. Исследования позволяют оценить влияние вечной мерзлоты на качество передачи и приема радиосигналов для связи и навигации.
Рассмотрены измерения, выполненные методами радиокомпарирования поля ДВ радиомаяка приводной радиостанции аэропорта п. Черский на высотах 200, 300 и 1000 метров над земной поверхностью и радиоимпедансные зондирования левобережной и правобережной сторон реки Колыма. Проведено сравнение рассчитанных значений модуля функции ослабления поля земной волны ДВ радиомаяка на двух импедансных радиотрассах с расчетными данными.
При решении задачи о поле, расположенного на Земле вертикального электрического диполя, будем пренебрегать переотражениями от всех неоднородностей, в том числе рельефа местности и импедансов, расположенными за точкой приема. При этом вертикальная компонента электрического поля будет удовлетворять приближенному граничному импедансному условию, в том числе для трассы с геометрическими неоднородностями.
1. Интегральное уравнение для функции ослабления над неоднородной трассой с учетом высоты приема сигнала
Для численного решения задачи о распространении радиоволн над однородной сферической поверхностью Земли при приеме на высоте удобно использовать метод расчета функции ослабления в виде ряда нормальных волн (ряд Фока) [1, 2]. Для расчета функции ослабления над неоднородными трассами наиболее обоснованным является метод численного решения интегрального уравнения [3]. Основное преимущество метода интегрального уравнения заключается в том, что он помимо высоты приема сигнала учитывает многокусочные импедансные разбиения трассы и рельеф местности.
Рассматривается поле
вертикального электрического диполя над реальной земной поверхностью. Вертикальная
компонента электрического поля Ez
над
геометрически и электрически неоднородной сферической поверхностью Земли с
началом в центре сферы радиуса a
удовлетворяет
волновому уравнению Гельмгольца: ![]() ,
где U – заданная функция,
описывающая источники; k=2pf/c
–
волновое число, здесь f
– частота, c - скорость света в
вакууме. На размеры препятствий нерегулярной трассы необходимо наложить условия
малости относительно длины волны: kz<1,
где z – высота препятствия. Будем считать,
что при выполнении таких условий для геометрических неоднородностей в задаче
применимо приближенное импедансное граничное условие на нерегулярной
поверхности S:
,
где U – заданная функция,
описывающая источники; k=2pf/c
–
волновое число, здесь f
– частота, c - скорость света в
вакууме. На размеры препятствий нерегулярной трассы необходимо наложить условия
малости относительно длины волны: kz<1,
где z – высота препятствия. Будем считать,
что при выполнении таких условий для геометрических неоднородностей в задаче
применимо приближенное импедансное граничное условие на нерегулярной
поверхности S: 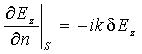 , где d
– приведенный поверхностный импеданс, для которого должно выполняться условие |d|2<<1,
n – внешняя по отношению
к поверхности Земли нормаль.
, где d
– приведенный поверхностный импеданс, для которого должно выполняться условие |d|2<<1,
n – внешняя по отношению
к поверхности Земли нормаль.
Запишем интегральное уравнение Кирхгофа для вертикальной составляющей электрического поля над неоднородной поверхностью и функции Грина j [4]:
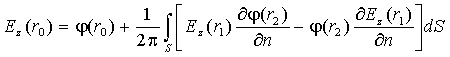 . (1)
. (1)
Здесь r0 – расстояние по прямой от источника до точки наблюдения, r1 – расстояние по прямой от источника до текущей точки интегрирования, r2 - расстояние по прямой от точки интегрирования до точки наблюдения. Пусть точка наблюдения будет расположена на высоте h над поверхностью Земли. Введем функцию Грина в виде суммы двух сферических волн, принимаемых в точке приема над земной поверхностью и в зеркальной точке:
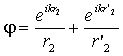 ,
,
где r'2 – расстояние от точки интегрирования до зеркальной точки наблюдения относительно земной поверхности, расположенной на глубине -h. Такой вид функции также является фундаментальным решением однородного волнового уравнения Гельмгольца.
Функция ослабления поля земной волны W вводится посредством формулы: Ez=W·E0, где E0=eikR/R – поле, создаваемое вертикальным электрическим диполем над идеально проводящей поверхностью на расстоянии R от источника. На практике модуль вертикальной составляющей электрического поля |Ez| можно приближенно связать с модулем функции ослабления |W| посредством формулы [5]:
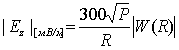 , (2)
, (2)
где Р – излучаемая мощность передатчика, кВт; R – расстояние от источника до точки приема, отсчитываемое вдоль поверхности Земли, км.
На основе интегральной формулы (1) с учетом всех указанных выше условий можно получить интегральное выражение для функции ослабления, учитывающей электрические и геометрические неоднородности при приеме на высоте h [3]:
где
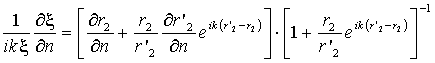 .
.
Здесь - x и D - расстояния вдоль поверхности Земли между источником и точкой интегрирования и между источником и точкой приема соответственно; r'0 – расстояние от источника до зеркальной точки наблюдения относительно земной поверхности.
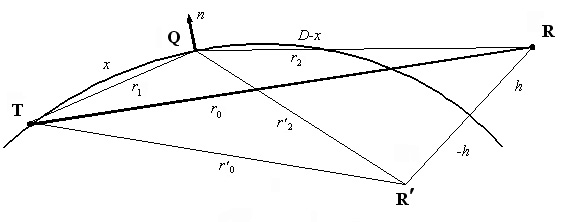
Рис. 1. Геометрия задачи (T – источник; Q – текущая точка интегрирования;
R – точка наблюдения; R¢ - зеркальная точка наблюдения
относительно земной поверхности).
2. Формулы для расчета функции ослабления
Для численного интегрирования уравнения (3) нами использовался алгоритм, основанный на методе конечных сумм [6]. На начальном условно ровном однородном участке трассы функция ослабления рассчитывается по формулам Зоммерфельда, которые также учитывают высоту приема [2, 7]. Уравнение (3) сводится к известному интегральному уравнению Хаффорда [8], если высоту приема h принять равной нулю.
Численное интегрирование уравнения (3) выполняется с
использованием квадратурной формулы трапеций с постоянным шагом интегрирования d=xi-xi-1. Область интегрирования [x0, xN.]
разбивается на N равных
частей. Шаг интегрирования выбирается достаточно малым, чтобы в его пределах
зависимость подынтегральной функции от расстояния хорошо аппроксимировалась
линейным законом. Для
каждой точки xi, i=1÷N, вычисляется значение функции
ослабления W(xi) по рекуррентной формуле, учитывающей
значения W во всех предыдущих точках. По
формулам Зоммерфельда расчеты W
проводятся на малых расстояниях x=aq, где q – угловое расстояние, которые определяются неравенством 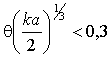 .
.
Ядро интегрального уравнения за счет множителя 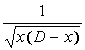 на обоих концах интервала интегрирования
обращается в бесконечность. Чтобы избавиться от этой неопределенности, делается
замена переменной в начале
на обоих концах интервала интегрирования
обращается в бесконечность. Чтобы избавиться от этой неопределенности, делается
замена переменной в начале ![]() и в конце
и в конце ![]() области численного интегрирования. Тогда
интегрирование разбивается на три части:
области численного интегрирования. Тогда
интегрирование разбивается на три части: 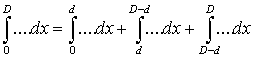 .
.
Запишем интегральное уравнение (3) в квадратурном виде:
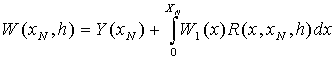 , (4)
, (4)
где xN ºD, 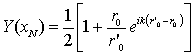 . Функция W1(x)
в уравнении (4) рассчитывается по методу уравнения Хаффорда [8] или по методу
уравнения Фейнберга [4], когда высота приема сигнала h=0. Методика численного решения
интегрального уравнения Фейнберга показана в работе [9]. Ядро интегрального
уравнения (3) запишется в виде:
. Функция W1(x)
в уравнении (4) рассчитывается по методу уравнения Хаффорда [8] или по методу
уравнения Фейнберга [4], когда высота приема сигнала h=0. Методика численного решения
интегрального уравнения Фейнберга показана в работе [9]. Ядро интегрального
уравнения (3) запишется в виде:
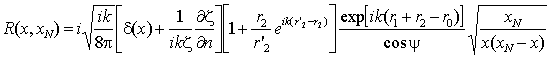 ,
,
где 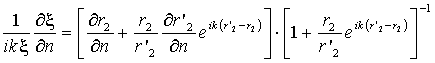 .
.
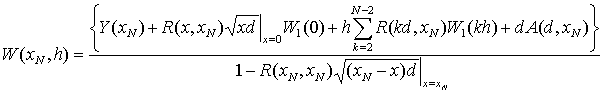 ; (5)
; (5)
![]() .
.
Соотношение (5) позволяет рассчитывать функцию ослабления W(x,h) в точке xN, зная ее значения без учета высоты приема во всех предыдущих точках радиотрассы.
3. Модельные расчеты
По интегральному соотношению (1) составлены алгоритм и программа расчета функции ослабления W(D,h). Выполнены сравнительные расчеты по ряду нормальных волн (ряд Фока) [1] и интегральному уравнению (3) для случая однородной по импедансу гладкой сферической поверхности (таблица 1). Расчеты проводились по формулам на частоте 200 кГц при приеме на высотах 1 км и 5 км для радиотрассы с однородными параметрами: относительная диэлектрическая проницаемость e=20, удельная проводимость s=10-2 См/м. Численное сопоставление показало, что расхождение рассчитанных разными методами функций W с учетом высоты приема h=5 км составляет по модулю менее 6,5%, а по фазе менее 0,1 радиана.
Таблица 1.
|
R, км |
|W| |
arg W, рад. |
|W|ФОК |
arg WФОК, рад. |
|
h=1 км 200 |
0,629 |
1,33 |
0,633 |
1,324 |
|
500 |
0,295 |
2,68 |
0,302 |
2,65 |
|
h=5 км 200 |
0,581 |
1,3 |
0,603 |
1,32 |
|
500 |
0,273 |
2,62 |
0,29 |
2,53 |
На рис. 2 представлены графики модуля функции ослабления, выполненные для частоты 257 кГц над однородной трассой (d=0,07·exp{-i540}) при приеме на разных высотах h. Расчеты по формуле Зоммерфельда выполнялись до расстояния 30 км. Как видно, по мере увеличения высоты приема сигнала модуль функции ослабления уменьшается. При этом отличие величины |W| с учетом высоты приема до 200 метров от величины |W| без учета высоты приема не превышает 5,6%. Таким образом, для данной трассы высотой приема до 200 метров при эксперименте можно пренебречь.
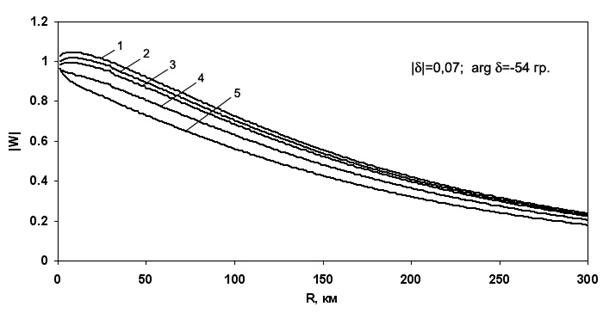
Рис. 2. Графики |W| над однородной трассой с сильно индуктивным поверхностным импедансом для различной высоты приема h:
1 – h=0 м; 2 – h=100 м; 3 – h=200 м; 4 – h=500 м; 5 – h=1000 м.
Рассмотрим эффекты распространения ДВ радиоволн над геометрической неоднородностью в виде Гауссовой горы, которая выражается формулой:
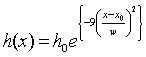 . (6)
. (6)
Здесь h0 – высота горы (в наших расчетах 0,5 км), w – ширина горы (10 км), x0 – расстояние от источника до середины горы (50 км). Расчеты по формуле (3) выполнялись на частоте 100 кГц для электрических свойств подстилающей среды трассы: относительная диэлектрическая проницаемость e=10, удельная проводимость s=5·10-3. На рис. 3 показаны результаты расчета модуля и аргумента функции ослабления при приеме на высотах h=0, 1, 3 и 5 км. Отметим, что геометрическая неоднородность начинает оказывать влияние на процесс распространения радиоволн в момент ее появления на трассе, а заканчивает в зависимости от высоты приема, чем выше препятствие, тем дальше наблюдается влияние неоднородности. Наличие Гауссовой горы (6) приводит к возмущениям уровня поля без учета высоты приема сигнала в пределах 19%, а по фазе в пределах 0,14 радиана. При приеме на высоте 1 км возмущение из-за горы находится пределах 15,5% для уровня поля и в пределах 0,11 радиана для дополнительной фазы.
Рис. 3. Результаты расчетов |W| и arg W на частоте 100 кГц над неоднородностью в виде Гауссовой горы с высотой h0=0,5 км.
4. Численные и экспериментальные результаты
Измерения на разных высотах полета выполнялись на Северо-востоке Якутии в районе п. Черский (161°20¢E, 68°44¢N). Радиокомпарирование выполнялось на частоте 257 кГц (частота дальнего привода аэропорта п. Черский) с борта самолета АН-2 на двух трассах: над равнинной трассой Черский-Чокурдах на постоянных высотах полета 1000 и 200 метров и над гористой трассой Черский-Певек на высотах полета 1000 и 100 метров, каждая трасса имеет протяженность около 100 км (рис. 4). Радиостанция излучала электромагнитное поле вертикальной поляризации, распространяющееся в дневное время земной волной. Район исследования характеризуется в первую очередь наличием многолетнемерзлых пород.
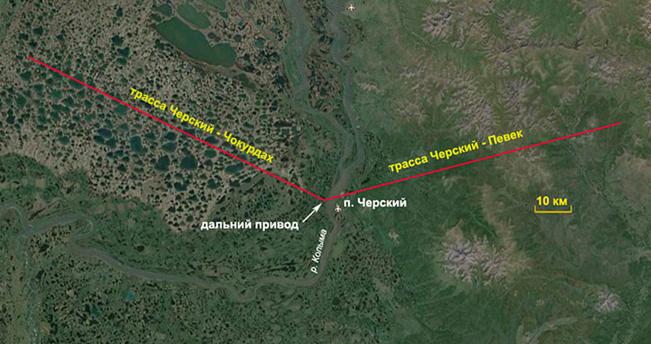
Рис. 4. Схема выполнения измерений с борта самолета на
двух радиотрассах:
равнинная Черский-Чокурдах и гористая Черский-Певек.
Трасса Черский-Чокурдах проходит над равнинной тундровой местностью с перепадом высот 30-40 метров с чередующимися тундровыми озерами. На частоте 257 кГц путем непосредственного измерения с помощью прибора ИПИ-300 получено, что на озерах и реке Колыма поверхностный импеданс имеет сильно индуктивный характер, фаза импеданса jd составила -56º ÷ -67º, модуль импеданса |d| находился в пределах 0,031 ÷ 0,066 [10, 11]. Измерения поверхностного импеданса на участках суши дали результаты по модулю в пределах 0,08 ÷ 0,12, по фазе -47º ÷ -53º. Для расчета поля были приняты средние значения модуля и фазы поверхностного импеданса, так как озера и участки суши имели равномерное чередование (|d|=0,075, arg d=-48º).
На рис. 5 приведены результаты измерений модуля функции ослабления |W| методом радиокомпарирования с борта самолета на трассе Черский-Чокурдах при полете на высотах 200 и 1000 метров и рассчитанные значения модуля функции ослабления. Приведенные графики показывают, что расчеты модуля функции ослабления, выполненные по формуле Фока для однородной трассы с измеренным значением импеданса, дают вполне хорошее согласие с данными радиокомпарирования при приеме сигнала на высоте 200 м. Отличия измеренных значений |W| от рассчитанных значений не превышают 16,5%. Для высоты приема 1000 метров расхождения результатов измерений и расчетов |W| имеют большие отличия особенно в начале (до 50%) и в конце радиотрассы (до 60%). Очевидно, что радиотрассу желательно рассматривать, как многокусочную. Измерения поверхностного импеданса проводились лишь в окрестностях п. Черский до максимального расстояния 15 км от приводной радиостанции. Поэтому нам не были известны точные электрические свойства всей радиотрассы.
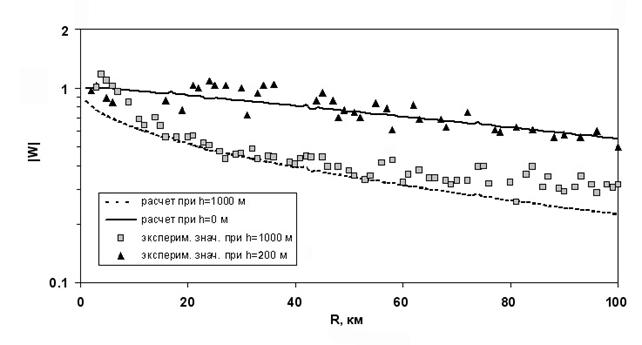
Рис. 5. Графики измеренных и
расчетных значений модуля функции ослабления
на разных высотах приема сигналов
для трассы Черский-Чокурдах.
Рельеф трассы Черский-Певек гористый, абсолютные отметки гор достигают 700 метров. Высота гор соизмерима с длиной волны для частоты приводной станции (l=1167 м), поэтому рельеф местности существенно влияет на процесс распространения радиоволн. По данным измерений поверхностного импеданса, учитывая особенности рельефа местности радиотрассы, а также данные карты геоэлектрических разрезов Северо-Востока России [10], выделено пять импедансных участков (таблица 2).
Таблица 2.
|
Импедансные участки, км |
|d| |
arg d, градусы |
|
R = 0-5 |
0,063 |
- 76 |
|
R = 5-10 |
0,106 |
- 68 |
|
R = 10-27 |
0,134 |
- 40 |
|
R = 27-42 |
0,106 |
- 68 |
|
R = 42-100 |
0,135 |
- 54 |
На рис. 6 приведены экспериментальные и рассчитанные по уравнению (3) значения модуля функции ослабления для радиотрассы Черский-Певек при приеме сигнала на высотах 1000 и 100 метров над уровнем земной поверхности. Модельные расчеты зависимости |W| от высоты показали, что при высоте приема до 200 м над поверхностью наблюдаются минимальные расхождения с наземными измерениями. Отличие измеренных значений ослабления поля находится в среднем в пределах 20% относительно рассчитанных значений на обеих высотах полетов. Близость расчетов и измерений показывает вполне приемлемую модель трассы распространения для прогнозирования поля на разных высотах приема при хорошо подобранных электрических свойствах радиотрассы. Значительные расхождения между расчетными и экспериментальными значениями |W| в некоторых точках приема объясняются тем, что расчетная модель многокусочной радиотрассы не полностью учитывает реальное распределение электрических свойств трассы и рельефа местности. Измерения напряженности поля выполнялись в конце октября месяца, когда активно происходило замерзание верхнего слоя, поэтому электрические свойства подстилающей среды также могли быстро меняться.
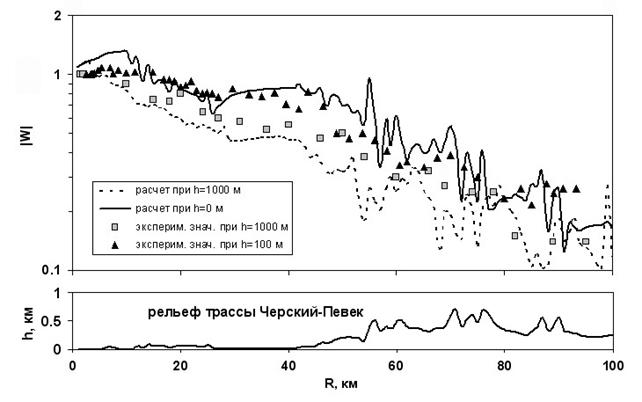
Рис. 6. Графики измеренных и
расчетных значений модуля функции ослабления
на разных высотах приема сигналов
для трассы Черский-Певек.
6. Заключение
Использование интегрального уравнения (3) является обобщенным методом расчета функции ослабления для электрически и геометрически неоднородных трасс с учетом высоты приема сигнала. Метод нормальных волн [1], для сильно индуктивных импедансов требует отдельного рассмотрения случая вырождения корней трансцендентного уравнения, учитывающего граничное условие, Тогда как расчет по методу интегрального уравнения (3) выполняется для всех физически возможных импедансов без специального рассмотрения особых случаев. Установлено, что измерения напряженности поля на борту самолета при полете на высоте до 200 метров практически не отличаются от измерений на земной поверхности. Экспериментальная проверка эффективности прогноза поля на реальных мерзлотных радиотрассах показала среднюю погрешность прогноза |W| на уровне ±20%. Сравнение измеренных и рассчитанных значений |W| дало хорошее соответствие модели многокусочной радиотрассы для расчета полей над неоднородными средами с учетом высоты приема сигнала.
Литература
-
Фок В.А. Проблемы дифракции и распространение электромагнитных волн. -М.: Советское радио, 1970. 519 с.
-
Макаров Г.И., Новиков В.В., Рыбачек С.Т. Распространение электромагнитных волн над земной поверхностью. -М.: Наука, 1991. 196 с.
-
Тихомиров Н.П. Формулы для функции ослабления на высоте над электрически и геометрически неоднородными трассами // Труды XIV Всесоюзн. Конф. по распространению радиоволн. Ч. 2. М., 1984. С. 249-250.
-
Фейнберг Е.Л. Распространение радиоволн вдоль земной поверхности. -М.: Физматлит, 1999. 496 с.
-
Жиряков В.Н., Рубинштейн В.И., Штейнберг А.А. Измерение модуля функции ослабления с борта самолета // Проблемы дифракции и распространения волн. - Л.: Изд-во ЛГУ, 1990. Вып. 23. С. 185-188.
-
Дембелов М.Г. Функция Зоммерфельда поля над импедансной плоской поверхностью. // Известия высших учебных заведений. Физика. 2013. Т. 56. № 8-2. С. 79-81.
-
Hufford G.A. An integral equation approach to the problem of wave propagation over an irregular surface // Quarterly of Applied Mathematics. 1952. V. 9. pp. 391-404.
-
Дембелов М.Г.¸ Башкуев Ю.Б. Метод численного решения обобщенного интегрального уравнения Фейнберга для геометрически и электрически неоднородных трасс // Физика волновых процессов и радиотехнические системы. 2008. Т. 11. № 1. С. 89-94.
-
Башкуев Ю.Б., Мельчинов В.П., Дембелов М.Г. и др. Влияние электрических свойств криолитозоны на распространение земной волны в высоких широтах // Геомагнетизм и аэрономия. 2006. Т. 46. № 4. С. 536-546.
-
Башкуев Ю.Б., Дембелов М.Г., Поляков М.А., Пылаев А.А. Определение электрических параметров слоистой подстилающей среды по результатам радиогеофизических измерений // Радиотехника и электроника. 2015. Т. 60. № 6. С. 598-603.