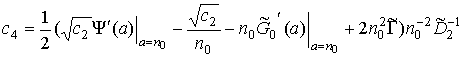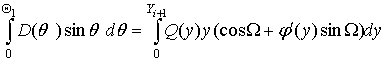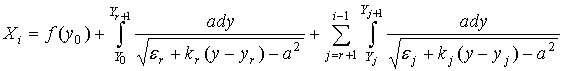| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9, 2005 |
ВОССТАНОВЛЕНИЕ КОЭФФИЦИЕНТА ПРЕЛОМЛЕНИЯ НЕОДНОРОДНОЙ
СРЕДЫ С ОСЕВОЙ СИММЕТРИЕЙ ПО АМПЛИТУДНОЙ ХАРАКТЕРИСТИКЕ ПРОШЕДШЕГО ПОЛЯ
А.С. Венецкий,
В.А. Калошин
Институт радитехники и электроники РАН
Получена 19 сентября 2005 г.
В статье рассмотрена задача нахождения закона изменения коэффициента преломления ограниченной неоднородной среды с осевой симметрией по заданной амплитудной характеристике прошедшего через нее поля. Предложены и исследованы две аналитические методики получения решения в приближении геометрической оптики. Первая из них основана на использовании разложения всех параметров задачи по степеням отношения расстояния от оси системы к толщине среды на оси. Вторая – на использовании слоистой модели неоднородной среды, причем внутри каждого слоя коэффициент преломления полагается постоянным либо меняется по линейному закону. Первая методика может применяться для градиентных сред, а вторая как для слоистых, так и градиентных сред (при использовании достаточно большого количества слоев).
В задачах диагностики неоднородных сред, при синтезе градиентных или слоистых линзовых антенн необходимо найти профиль диэлектрической проницаемости или, что эквивалентно при постоянной магнитной проницаемости - коэффициента преломления. Обычно в качестве исходных данных используется фазовая характеристика прошедшего поля, однако не всегда это возможно. В данной работе рассматривается задача определения профиля коэффициента преломления осесимметричной ограниченной неоднородной среды по амплитудной характеристике выходного фронта. Падающий фронт здесь и далее предполагается сферическим с источником излучения - на оси симметрии среды, при этом его диаграмма направленности предполагается известной.
В цилиндрической системе координат, связанной с осью симметрии среды z , среда характеризуется тремя функциональными зависимостями: функция z=f(r) , описывающая первую границу среды (на которую падает сферический фронт), z=j(r) – функция, описывающая вторую границу среды, и n(r) –коэффициент преломления среды.
В силу осевой симметрии задачи здесь и далее достаточно рассмотреть ход лучей в одной из плоскостей, проходящих через ось симметрии среды (рис.1).
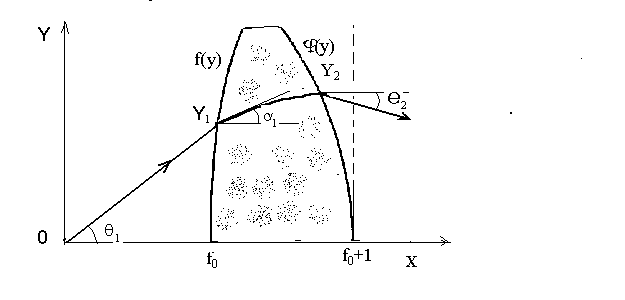
Рис.1
Уравнение семейства лучей в этой плоскости имеет вид [1]
где а – лучевой параметр, n(y) – коэффициент преломления, f(y)и j(у) – формы
сечения поверхностей среды. Здесь и далее осевая толщина среды принята за 1.
Диаграмма направленности падающего поля предполагается известной и равной D(q1), где q1- угол, отсчитываемый от оси источника, совпадающей с осью симметрии среды. Пусть на второй поверхности среды прошедшее поле имеет функцию распределения мощности Q(r). Требуется определить n(y).
Из уравнения лучей (1) получаем соотношение
когда луч монотонный и
когда луч немонотонный. Верхний предел р в последних двух интегралах есть точка максимума луча. При у=р знаменатель в подынтегральных функциях обращается в 0.
Из закона преломления на левой и правой границах можно получить уравнения
Предполагается, что выходящий лучевой фронт удовлетворяет закону:
где b(у) будет найдено из условия энергетического баланса.
Постановка задачи состоит в нахождении n(y), удовлетворяющего интегральному уравнению (2) или (2а) и условиям (3), (4), (5) для всех лучей, прошедших через среду, причем f(y) и j(у) предполагаются заданными. Будем также предполагать, что выходящий лучевой фронт является регулярным (не образует каустик).
Будем использовать две методики решения задачи. Первая методика, как и работа [2], основана на разложении параметров задачи в ряды по четным степеням у. Вторая методика использует слоистую модель непрерывной среды, причем внутри каждого слоя диэлектрическая проницаемость предполагается постоянной, либо меняется по линейному закону. Сначала будем искать решение, используя первую методику. Для этого представим
где no2=n2(0) – задано, коэффициенты f2k, j2k – заданы, с2k (k=1,2,3,…) – неизвестные коэффициенты, подлежащие определению, причем с2>0 (n(y) убывает).
Соотношение (5), описывающее закон отображения, представим в виде:
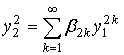 (7)
(7)
где b2к (к=1,2,…) - заданы.
Согласно разложениям (6), соотношение (3) можно записать в виде
где a2=no2-a2, а первые три g2k находятся следующим образом:
Преобразуем левую часть соотношения (3). Для этого представим sinq1, cosq1, f¢(y1) в виде разложений по степеням у1 :
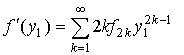 ,
,
![]()
![]()
где
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Тогда
![]()
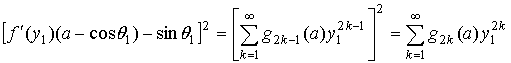 ,
,
где
g1(a)=2f2(a-1)-n1, g3(a)=4f4(a-1)+2f2k2+n3, g5(a)=6f6(a-1)+4f4k2-2f2k4-n5,
g2=g12, g4=2g1g3 , g6=2g1g5+g32.
Из (8) следует, что для центрального луча (у1=0) a=no и a=0. Так как g2+c2>0 при всех значениях а, то можно обратить (8) относительно у1, т.е. представить у12 в виде ряда по степеням a2:
где
![]() ,
,
![]() ,
,
![]()
Из закона отображения (7) и разложения (8) можно получить разложение для у2:
где
А2=b2А1, В2=b2В1+b4А12 , ![]() .
.
Преобразуем уравнение (2). Используя разложения (6), подынтегральное выражение в (2) представим в следующем виде:
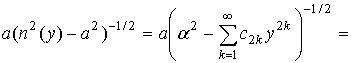
где р – корень уравнения n2(p)-a2=0 . Из представления (6) следует, что
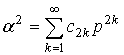 .
.
Тогда по формуле обращения рядов имеет место разложение:
и, следовательно,
Коэффициенты R2k, V2k (k=0,1,2,…) выражаются через коэффициенты рядов (6) и (14). Так, первые три имеют вид
Ro=a2 /p2, R2=c4+p2c6 , R4=c6 ,
Vo=p/a , V2= -1/2p3/a3(c4+p2c6) , V4=3/8p5/a5(c4+p2c6)2-1/2p3/a3c6. (15)
Используя разложение (12), интеграл в (2) можно представить в виде суммы интегралов:
а интеграл в (2а)
где
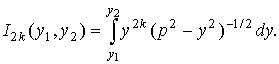
Все интегралы I2k выражаются явно:
![]()
![]() ,
,
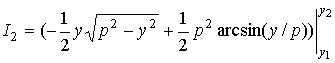 ,
,
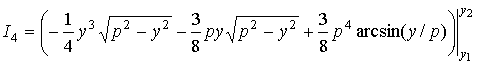 , . . .
, . . .
Подставляя вместо у1, у2, р в последних формулах выражения (9), (10) и (14), заменяя arcsin(y/p) и (p2-y2)1/2 в них формулами Тейлора с нужным числом степеней a и приводя в (17) члены с одинаковыми степенями a, получаем :
где для класса монотонных лучей
![]() ,
,
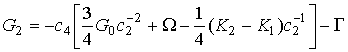 ,
,
![]() ,
, ![]()
![]() ( i=1,2)
( i=1,2)
![]() ,
,
![]() ,
,
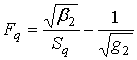
А для класса немонотонных лучей
![]() ,
,
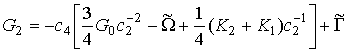 ,
,
![]() ,
,
![]() ,
,
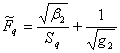 .
.
В приведенные выражения входят неизвестные коэффициенты b2 и b4 из разложения (7). Выразим их, используя уравнение энергетического баланса. Вычислим мощность, заключенную в элементарной лучевой трубке до и после прохождения среды. До прохождения среды она будет равна D(q1)sinq1dq1dy, где sinq1dq1dy - элемент телесного угла в сферической системе координат. В силу осевой симметрии можно перейти от цилиндрических координат r,y,z к декартовым координатам х,у. Тогда мощность, заключенная в лучевой трубке после прохождения среды будет равна
![]() ,
,
где у – координата точки выхода луча из среды, х=j(у), c - угол между касательной плоскостью к поверхности среды в точке выхода луча из среды и плоскостью, ортогональной к лучевой трубке. Используя геометрическое соотношение
![]() , где
, где
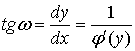 , q2 – угол выхода луча из среды,
получаем
, q2 – угол выхода луча из среды,
получаем
![]() .
.
Приравнивая выражения для мощности в лучевой трубке до и после прохождения среды и сокращая на dy, получаем уравнение энергетического баланса
Будем предполагать, что в некоторой окрестности оси имеют место разложения
Q(y) = Q0 ( 1+ q2y2 + q4y4 +…) , (21)
где D0, Q0 константы, определяемые из условия нормировки. Имеет значение только отношение этих констант. Разложения содержат только четные степени в силу симметрии. С точностью до членов 2-го порядка малости соотношение (19) принимает вид:
D0q1dq1= Q0ydy
Интегрируя обе части, получаем
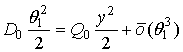
В последнем представлении и далее координату выхода луча из среды будем обозначать через у2 вместо у, чтобы отличать от координаты входа луча в среду, которую будем обозначать через у1. Учитывая, что в первом приближении
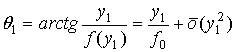 ,
,
выражение (22) можно записать в виде
Или, возводя в квадрат:
где
![]() .
.
Выразим теперь отношение коэффициентов D0/Q0 через коэффициенты разложений коэффициента преломления среды. В малой окрестности оси можно считать закон изменения квадрата коэффициента преломления квадратичным
![]() .
.
В этом случае интеграл, входящий в уравнение лучей (1) можно выразить явно. Предположим сначала, что луч в среде монотонный. Тогда из уравнения лучей (1) можно получить:
где
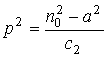 . Учитывая, что с точностью до членов 2-го
порядка малости правая часть соотношения (25) равна 1 (см.
6), параметр а=no (см. 29), можно из соотношения (25)
получить
. Учитывая, что с точностью до членов 2-го
порядка малости правая часть соотношения (25) равна 1 (см.
6), параметр а=no (см. 29), можно из соотношения (25)
получить
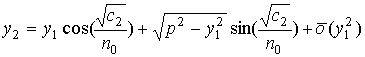 .
.
Используя соотношение (13) для представления р2 , окончательно получаем
где
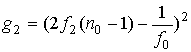 .
.
Сравнивая полученное выражение с представлением (23), находим
Легко показать, что аналогичные выражения для b2 и D0/Q0 справедливы и в случае немонотонных лучей.
Найдем теперь коэффициент b4. Он уже зависит от того, является ли луч внутри среды монотонным или нет. Для этого выпишем условие преломления луча на правой границе для монотонных и немонотонных лучей:
Из условия преломления на левой границе в виде (8), разложенного по степеням у1:
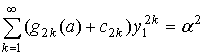 , где
, где
![]()
можно выразить лучевой параметр а в виде ряда по степеням у1:
Разлагая все слагаемые, входящие в условия (28) и (28а) в ряды по степеням у2 и q2 и оставляя только члены 1-го порядка, получаем
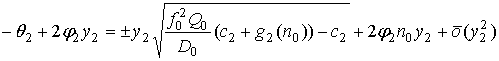
Откуда, получаем
![]()
где
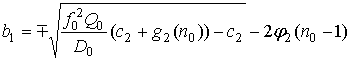 ,
,
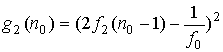 ,
,
или используя приведенное выше выражение для D0/Q0 можно получить
где знак «-» соответствует монотонному классу лучей, а знак «+» немонотонному.
Раскладывая члены, входящие в обе части соотношения (19) до степеней вплоть до 3-го порядка и интегрируя, получаем
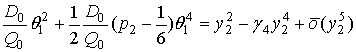 ,
,
где
![]() .
.
Обозначим через t левую часть последнего соотношения. Тогда его можно записать в виде
![]() .
.
А данную зависимость t от у2 можно представить в виде обратной зависимости у2 от t c помощью формулы обращения рядов:
![]() ,
,
которая, после подстановки t и приведения подобных членов дает выражение у2 через q1:
Используя выражение q1 через у1, а также представление f(y) рядом (6) можно записать:
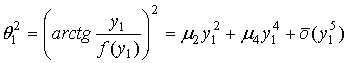 ,
,
где
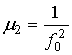 ,
,
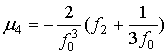 .
.
Подставляя выражение для q1 в (32) окончательно получаем:
Преобразуем теперь правую часть уравнения (2). Пусть Y(a)=j(y2)-f(y1). Используя разложения (6),(9) и (10) и приводя подобные члены, можно записать
где
![]() ,
,
![]() ,
,
![]() .
.
Интегральное уравнение (2) можно записать теперь в виде
где I(a) задается рядом (18), а Y(а) – рядом (35).
Тождество (36) выполняется при всех значениях параметра а , в том числе и при а=no, соответствующему центральному лучу. Приравнивая левую и правую части тождества (36), а также их производные при а=no получаем систему уравнений для определения c2k:
![]() ,
,
![]() ,
,
Первое уравнение системы (37) для монотонных лучей имеет вид:
а для немонотонных
Они являются трансцендентными относительно с2 и могут быть решены только численным методом. Путем тригонометрических преобразований оба этих уравнения можно свести к одному уравнению
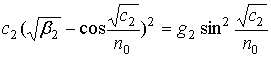 ,
,
которое содержит корни (38) и (38а). Найдя каким либо приближенным методом его корень надо подстановкой определить какому уравнению он удовлетворяет. Если (38) – то решение в монотонном классе лучей, если (38а) – то в немонотонном.
Второе уравнение системы (37) является линейным относительно с4. Приведем его решение для монотонных лучей:
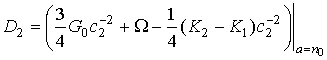 ,
,
![]() ,
,
И для немонотонных:
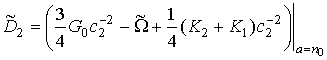 ,
,
![]() ,
,
![]() .
.
Остальные обозначения приведены после (18) и взяты при значении a=no.
Проиллюстрируем точность
представления искомого коэффициента преломления среды n(y) степенным рядом на примере среды с законом изменения
как в линзе Микаэляна [1], где n(y) задается
формулой
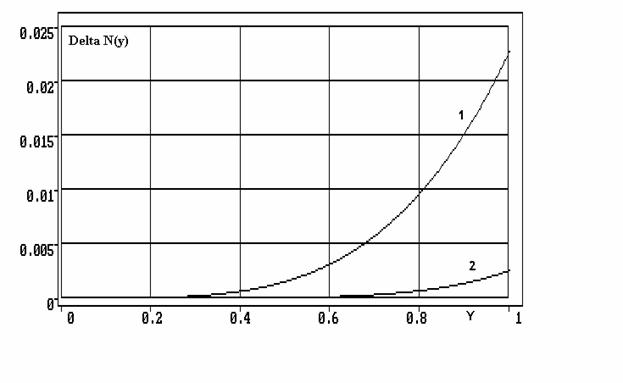
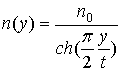 . (n0 =1.6, t=3). На рисунке 2 кривая 1 показывает разность между точной формулой и
рядом с двумя членами разложения, а кривая 2 – рядом с тремя членами
разложения.
. (n0 =1.6, t=3). На рисунке 2 кривая 1 показывает разность между точной формулой и
рядом с двумя членами разложения, а кривая 2 – рядом с тремя членами
разложения.
Рис.2
Перейдем к рассмотрению другой методики. Сначала будем искать решение n(y) в классе кусочно-постоянных функций. Сечение среды в этом случае будет представлять собой набор дискретных слоев равной высоты h с постоянным значением n(y) внутри каждого слоя (рис.3).
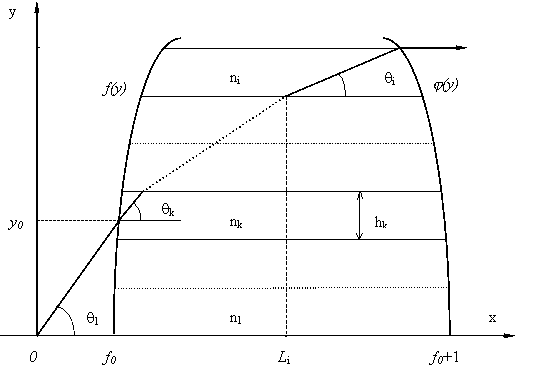
Рис.3
Предположим, следуя методу математической индукции, что мы уже определили i-1 слоев, т.е. знаем коэффициенты преломления nj, j=1,…,i-1. Опишем процедуру нахождения i-го слоя, т.е. ni. Рассмотрим элементарную лучевую трубку, образованную двумя близкими лучами, выходящими из источника, сечение которой на выходе из среды совпадает с искомым i-м слоем. Тогда для этой лучевой трубки уравнение энергетического баланса имеет вид:
где Dq - угол раскрыва лучевой трубки, Dу =h – толщина слоя, q1 – угол выхода из источника первого луча, известного из рассмотрения предыдущей лучевой трубки, W - угол выхода этого луча после прохождения среды, который также известен. Определяя из последнего уравнения Dq, рассмотрим луч, выходящий из источника под углом q1+Dq. Пусть слой, в который попадает этот луч имеет номер r. Найдем абсциссу Хi точки пересечения этого луча с искомым слоем i:
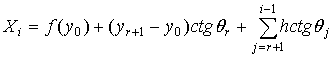
где уо-точка входа луча в среду, а qj , j = r,…,i-1 – углы наклона луча в соответствующих слоях, которые связаны соотношением
![]()
qr определяется из закона преломления на левой границе
где d=arctg(1/f¢(yо)) – угол наклона касательной к поверхности в точке пересечения луча с первой поверхностью к оси Ох.
В искомом слое угол qi определяется из соотношения
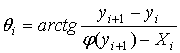 ,
,
и, следовательно,
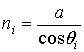 .
.
Далее переходим к определению по приведенной схеме i+1 слоя и т.д. Толщину слоя выбираем произвольно, а коэффициент преломления в первом слое считаем заданным.
Анализ развитых методик проведем на том же примере градиентной среды с плоскими поверхностями и законом изменения коэффициента преломления как в линзе Микаэляна. Предполагаем, что падающий фронт формирует диаграммму направленности D(q)=D0cosq , а источник отстоит от среды на расстояние f0=0.5.
На рисунке 4 приведены графики разности между n(y), восстановленного по данной методике и n(y) в линзе Микаэляна. Числа над кривыми означают толщину слоя. Результаты нельзя признать удовлетворительными, т.к. величина ошибки очень велика ( на два порядка хуже ошибки, чем для предыдущей методики) и не падает с ростом числа слоев. Таким образом, эта методика неэффективна для градиентных сред.
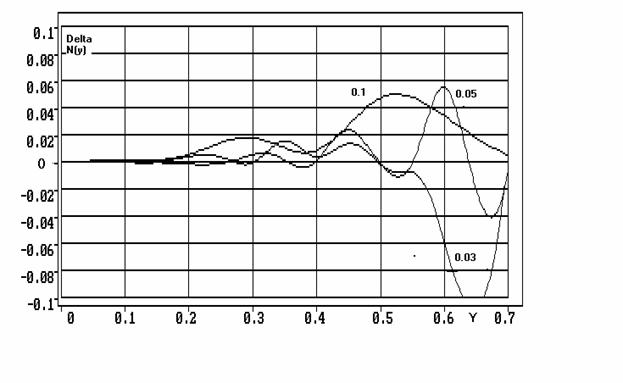
Рис.4
Используем другую модель среды для решения задачи. Будем искать решение n2(y) в классе кусочно-линейных функций. Сечение среды в этом случае будет представлять собой набор дискретных слоев равной высоты h , причем в i-м слое диэлектрическая проницаемость меняется по линейному закону:
![]() ,
,
![]()
Как и ранее будем определять i-й слой в предположении, что все предыдущие i-1 слоев уже известны. Рассмотрим луч, выходящий из источника, который после прохождения через среду выходит точно в конце i-го слоя в точке уi+1.
Найдем связь между точкой уi+1 и углом выхода луча из источника. Для этого проинтегрируем соотношение (19).
Интеграл в левой части представляет собой известную функцию от верхнего предела q1 , а интеграл в правой части зависит от верхнего предела Yi+1 , а также от входящей в подынтегральное выражение функции W(у) – угла наклона луча, выходящего из среды в точке с координатой у. В силу предположения индукции слои вплоть до слоя i уже найдены и, следовательно, W(у) известна на интервале 0<y<yi и неизвестна на интервале yi<y<yi+1. Обозначая интеграл в правой части (42) через Ii и разбивая область интегрирования (0,уi+1) на две: (0,уi) и (уi,yi+1), можно представить его в виде суммы двух:
Ii=Ii-1+DIi
Интеграл Ii-1 известен из предыдущего шага итерации, а интеграл DIi вычислим в предположении, что W(у) на интервале (уi,yi+1) меняется линейно, причем на первом шаге итерации линейно экстраполируем функцию W(у) с предыдущего интервала.
Разрешим уравнение (42) относительно q1 . Рассмотрим путь луча, выходящего из источника под данным углом q1. Пусть слой, в который попадает этот луч имеет номер r. Найдем абсциссу Хi точки пересечения этого луча с искомым слоем i :
где уо – точка входа луча в среду, a=n(yo)cosqr – лучевой параметр, qr определяется из закона преломления (41). Выражая интегралы, входящие в (43) явно, получаем:
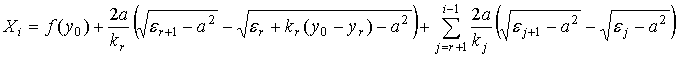
Чтобы избежать неопределенностей при малых kj , лучше использовать эквивалентное выражение:
![]()
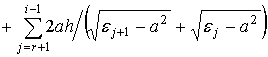
В i-м слое искомое ei+1 найдем из условия, что рассматриваемый луч должен выйти из среды в точке границы слоя уi+1:
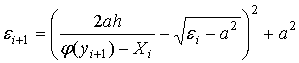
Теперь из закона преломления на границе в точке уi+1 можно найти W1=W(уi+1) - уточненное значение угла наклона преломленного луча к оси ОХ :
![]()
где d=arctg(1/j¢(yi+1)), a - угол наклона касательной к лучу в точке уi+1 до преломления.
Введем в рассмотрение функцию рассогласования F1(W1)=W1-W0 , где W0 – угол наклона преломленного луча, полученного на первом шаге в результате линейной экстраполяции. Методом Ньютона находим следующее уточненное значение W2=W1-F1/F1¢. Найдя W2 , вычисляем снова интеграл DIi и находим из уравнения (42) новое значение q1. После чего повторяем описанную процедуру. На шаге итерации номер N:
WN=WN-1-FN-1/FN-1¢
Производную F¢(W) находим приближенно, задавая малое приращение к W. Процедура заканчивается, когда ïWN-WN-1ï< t , где t - заданная малая погрешность. Полученное на данном шаге значение ei+1 и будет искомым значением диэлектрической проницаемости в точке уi+1, а внутри слоя e меняется по линейному закону. Далее по приведенной схеме определяем следующий i+1 слой и т.д.
Для проверки точности определения по приведенной методике коэффициента преломления среды был рассмотрен тот же пример, что и ранее. На рисунке 5 приведен график разности восстановленного n(y) и заданного. Найденная оптимальная величина шага равна 0.05.
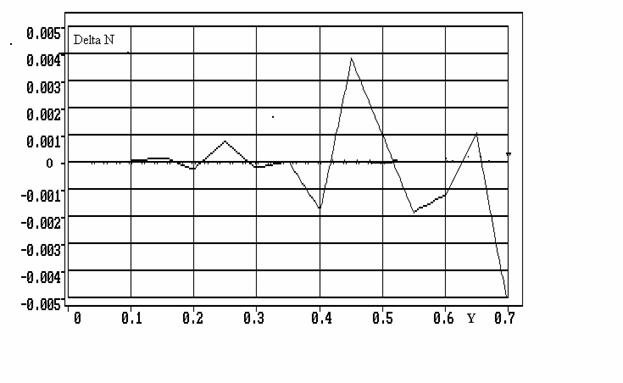
Рис.5
Как видно из рисунка, использование линейно-ломаной аппроксимации коэффициента преломления среды позволяет примерно на порядок уменьшить ошибку восстановления, однако не позволяет обеспечить точность, сравнимую с точностью степенного ряда (см. рис. 2).
Литература.
1. Зелкин Е.Г., Петрова Р.Н., Линзовые антенны, М., Сов.Радио, 1974 г.
2. Венецкий А.С., Калошин В.А., Синтез градиентной линзовой антенны с осевой симметрией и криволинейной формой преломляющих поверхностей, Радиотехника и электроника, 1997, том 42, №12, с.1452-1458.
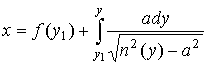
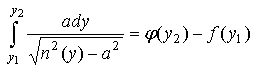
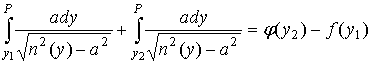
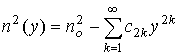 ,
, 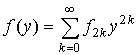
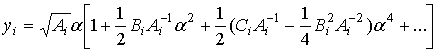 ,
,  ,
,  .
.
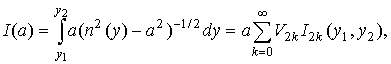
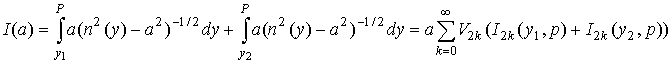
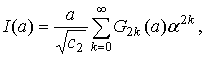
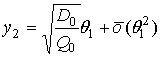
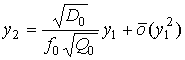 (
(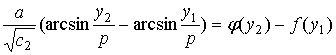
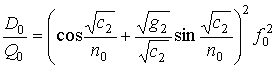
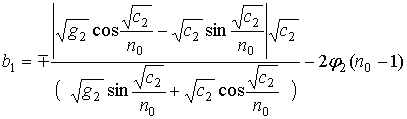 ,
,
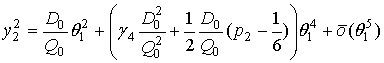 .
.
 ,
,
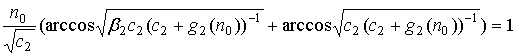
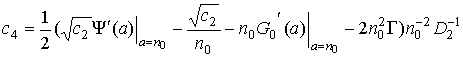 ,
,