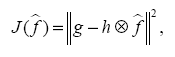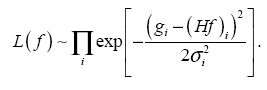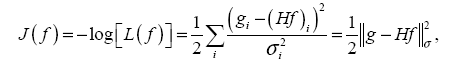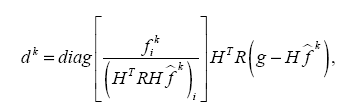|
"ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 9, 2008 |
Математическое моделирование в
задачах обработки данных в системах радиовидения
Ю.А. Пирогов, А.Н.
Боголюбов, В.В. Гладун, Р.А. Гущин,
И.Е. Могилевский, Н.Е.Шапкина
Московский государственный университет им. М.В. Ломоносова
Центр магнитной томографии и спектроскопии
Получена 25 сентября 2008 г.
Рассматриваются различные математические методы обработки данных в системах радиовидения с целью улучшения разрешения полученных изображений. В результате анализа ряда алгоритмов для численного эксперимента выбирается алгоритм восстановления пространства изображений (ISRA). Приводятся результаты расчетов для тестовых задач сверхразрешения в системах радиовидения.
Ключевые слова: радиовидение, сверхразрешение, обработка изображений.
Введение
В данной работе рассматриваются методы обработки данных, получаемых в системах радиовидения. Подобные системы в настоящее время находят применение во все большем количестве прикладных задач, постепенно вытесняя системы ИК-диапазона. Их основным преимуществом таких систем по сравнению с ИК-системами является независимость от метеорологических условий, обеспечивающая возможность получения сравнительно качественных изображений даже в тех случаях, когда получение изображения ИК-методами невозможно. Подобные системы применяются в управлении авиационным трафиком, экологическом мониторинге, пассивной локации, детектирования скрытого под одеждой оружия в публичных местах и т.п.
Однако в связи с использованием большей длины волны такие системы проигрывают системам ИК и видимого диапазона по таким параметрам, как угловое разрешение и скорость получения информации. Угловое разрешение для радиовидения ограничено рэлеевским пределом
[1], где λ - рабочая длина волны, D - входная апертура. Повысить угловое разрешение можно двумя путями: варьируя параметры λ и D или применяя методы сверхразрешения, основанные на математической обработке измеренных радиометрических данных. Цель такой обработки — компенсировать искажения изображения, вызванные конечным угловым разрешением системы. В то время как уменьшение рабочей длины волны и увеличение апертуры является либо дорогостоящим, либо вообще невозможным по техническим причинам, метод сверхразрешения может быть применен практически в любой системе радиовидения. Поскольку наибольший практический интерес представляют системы реального времени, важным требованием, предъявляемым к алгоритмам сверхразрешения, является их быстродействие.
Скорость получения информации в системах радиовидения имеет фундаментальное ограничение. Чувствительность системы пропорциональна квадратному корню из постоянной времени интегрирования. Так, например, для двукратного повышения чувствительности необходимо в четыре раза увеличить время измерения. Характерным значением постоянной времени интегрирования является величина 0.1 с. В этом случае для построения изображения размером 128x128 точек необходимо около получаса. Для ускорения получения экспериментальных данных существует два потенциальных приема: во-первых, это улучшение характеристик используемых детекторов, усилителей и т.д. Во-вторых, это увеличение числа датчиков, т.е. использования линеек или матриц датчиков. В настоящее время используются системы, оснащенные количеством датчиков порядка одного или нескольких десятков, что заведомо недостаточно для получения изображения без использования подвижных частей установки. Различные способы реализации влияют на геометрию получаемых данных. Таким образом, может возникать необходимость в интерполяции экспериментальных данных на регулярную прямоугольную сетку для построения полученного изображения.
Математическая постановка задачи
Рассмотрим модель формирования изображения на выходе системы. Она описывается классическим интегральным выражением для линейных систем
(1)
где
— двумерный вектор мировых координат;
- двумерный вектор в лабораторной системе координат;
- исследуемое распределение радиояркостной температуры,
- аппаратная функция системы;
- аддитивный шум;
- результат измерений, область D представляет собой кольцо. В дальнейшем будем пользоваться более краткой записью
(2)
Постановка задачи сверхразрешения заключается в следующем: основываясь на экспериментальных данных
,
и, возможно, дополнительной (априорной) информации, получить решение
, близкое к исходному распределению
. Чаще всего в качестве критерия сходимости приближенного решения к точному берется близость к нулю функционала вида
где
— есть норма в
, поскольку предполагается, что n – гауссов белый шум [3].
Рассматриваемая задача, представляющая собой интегральное уравнение Фредгольма 1-го рода, является некорректно поставленной. Даже небольшой шум во входных данных приводит к сильному искажению получаемых результатов.
Для одномерного случая типичен выбор функции
в качестве модельной аппаратной функции. Если отсутствует шум, то есть
, задача восстановления изображения может быть решена точно с помощью разложения по собственным функциям интегрального оператора с ядром
[3]. Однако построенное таким образом решение является неустойчивым, наличие даже небольшого шума приводит к сильным отклонениям от точного решения.
Методы решения
Существует классический, наиболее обоснованный с теоретической точки зрения, метод решения уравнения (1) с использованием процедуры регуляризации Тихонова.
Однако для практического применения он подходит плохо, так как требует введения поправок, получаемых либо эмпирическим путем, либо на основе достаточно полных априорных данных, что делает практически невозможным создание полностью автоматизированных систем. В то же время разработано большое количество практических алгоритмов, преимущественно итерационных, не требующих таких данных.
В работах [2,4-6] проведено сравнение различных алгоритмов и выявлено преимущество нелинейных итерационных алгоритмов, изначально нацеленных на задачи обработки изображения — это алгоритмы восстановления пространства изображений (ISRA) и Люси-Ричардсона.
Алгоритм восстановления пространства изображений (ISRA)
При построении данного алгоритма предполагается, что шум n представляет собой случайную величину, подчиняющуюся распределению Гаусса с нулевым средним значением и дисперсией
[4]. Результаты измерений
(интенсивность в рассматриваемой i-ой точке) являются независимыми случайными величинами. Для каждого пикселя «i» результат измерения
будет суммой детерминированной величины
и случайной величины ni, где
. Вероятность того, что величина
принимает значение
, определяется как
Соответствующая логарифмическая функция правдоподобия есть
.
Решение
ищется путем минимизации евклидовой нормы с соответствующим весом для разности между результатами измерения и восстановленным средним значением интенсивности:
Обозначим диагональную матрицу с элементами
как R. Используя выражение для градиента
, получаем следующий итерационный алгоритм [3], основанный на методе градиентного спуска:
.
Достаточным условием сходимости такого алгоритма будет
[5]. Решение
, построенное с помощью данного итерационного процесса при
, формально может быть записано в виде
, что соответствует следующему условию минимума функционала первого порядка:
. Как уже отмечалось, восстановление функции, входящей в свертку, является некорректно поставленной задачей, поэтому полученное по данному алгоритму численное решение может быть неустойчивым. Более того, это решение может быть отрицательным, что не имеет физического смысла. Очевидно, при построении алгоритма следует наложить условие неотрицательности решения. Такому условию удовлетворяет итерационный алгоритм восстановления пространства изображения, являющийся модификацией метода градиентного спуска (Image Space Reconstruction Algorithm (ISRA) - алгоритм восстановления пространства изображений). Данный алгоритм может быть записан в виде:
(3)
где k— номер итерации, в качестве начального приближения берется
.
В аддитивной форме формула (3) может быть записана как
(4)
Из (4) видно, что это модифицированный алгоритм типа наискорейшего спуска, в котором направление спуска на каждой итерации задается формулой
где
представляет собой вектор, составленный из диагональных элементов матрицы. Легко видеть, что алгоритм гарантирует положительность решения, если начальное приближение положительно, так как аппаратная функция также положительна.
Вопрос о сходимости данного алгоритма исследован в работе [5], где показано, что последовательность (4) сходится к величине
, минимизирующей функционал
при дополнительном условии
.
В работе [2] проведено сравнение большого числа различных алгоритмов сверхразрешения. Алгоритм ISRA был признан по многим параметрам наиболее удачным для применения в задачах повышения разрешения систем радиовидения. Поэтому в настоящей работе предпочтение отдано именно этому алгоритму.
Интерполяция данных на прямоугольную сетку
Метод обратных расстояний с весом
(The inverse-distance weighted procedure)
Способ интерполяции, основанный на использовании величин, обратных расстояниям между узлами интерполяции, возведенным в некоторую степень, универсален, легко реализуем вычислительной машиной и понятен, а также обладает высокой степенью точности.
В рамках этого метода, искомое значение функции в каждой точке, для которой ищется решение, дается следующим образом:
,
где Pi – находимое значение в точке i;
Pj – значение в узле интерполяции j;
Dij – расстояние между i-той и j-той точками;
G – количество узлов интерполяции;
n – степень, в которую возводятся расстояния Dij.
Значение n фактически определяет, насколько влияет расположение j-тых точек на прогнозируемое значение Pi в точке i. По мере того, как n увеличивается, область влияния уменьшается до тех пор, пока в пределе не станет окрестностью точки i, из любой точки которой до i ближе, чем до любой из точек j. Когда n принимается равным нулю, метод становится идентичен обыкновенному нахождению среднего арифметического рассматриваемых величин.
Ватсон (Watson) и Филип (Philip) в 1985 году составили список некоторых ограничений использования этого метода, например, его нельзя использовать для случая радиальной симметрии, когда в результате такой интерполяции могут появиться элементы неоправданной линейности.
Экспериментально было показано, что для n
1 полная производная функции z=f(x,y) в узлах интерполяции претерпевает разрыв. Обычно значение n подбирается эмпирически для конкретной задачи. Значения 1,65 и 2 выбирались для n Келвеем (Kelway, 1974) и NOAA (1972) соответственно, для прогнозирования количества выпадающих осадков, в то время как модель ARMOS (1990) для обнаружения месторождений нефти рекомендует использовать значения n от 4 до 8.
Ватсон и Филип показали, как нужно модифицировать этот способ интерполяции, чтобы устранились ограничения, упоминаемые выше. В их методе степень n – функция как расстояний Dij, так и погрешностей входных величин.
Интерполяция с минимизирующей погрешность
функцией (Punctual Kriging (PKG))
В рамках этого метода значение в каждом узле интерполяции берется с весом, а погрешность минимизируется путем решения системы следующих уравнений:
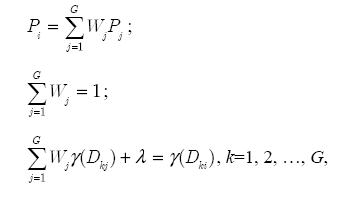
где Wj – поправочные коэффициенты значений Pj , учитывающие близость каждого из узлов j к точке i ;
λ – переменная, вводимая для минимизации погрешности;
γ(Dkj) – функция, восстанавливающая значение в точке, лежащей между точками k и j.
Даже в том случае, когда функция γ неизвестна, система уравнений все же может быть решена, если предположить, что искажающие эффекты отсутствуют. В этом случае она определяется следующим образом:
,
где f – функция от Dkj , вид которой определяется начальными условиями;
A – константа.
Количество таких функций f, которые могут быть использованы для вычисления функции γ, сильно ограничено. МакБретни (McBratney) и Вебстер (Webster) в 1986 составили список таких функций и дали объяснение, почему остальные функции не подходят. В самом простом случае, когда f(Dkj) = Dkj, уравнение
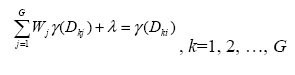
может быть заменено следующим:
,
где β – константа (нет необходимости находить β или λ для того, чтобы вычислить значения Pi).
В этом упрощении функция γ линейна. Оно применимо к тем случаям, когда количество узлов сетки интерполяции недостаточно для точного определения этой функции.
Исследования показали, что несмотря на то, что вид функции γ влияет на погрешности, на сами интерполируемые величины она оказывает небольшое влияние. Кук (Cooke) и Мостахими (Mostaghimi) в 1992 использовали линейную функцию γ для того, чтобы оценить значение осадков и получили значения, которые незначительно отличались от тех, что прогнозировались путем использования стандартных методов.
Интерполяция с помощью триангуляции на плоскости
(Bivariate Interpolation)
Для стандартного компьютерного дизайна (CAD) или тестирования (CAT), огромное количество входных данных внутри многомерной матрицы должно быть итеративно проанализировано за короткое время и, желательно, с низкими материальными затратами. Непосредственные вычисления для получения дополнительных входных данных, которые не располагаются в узлах матрицы, дорогостоящи. Это является достаточной причиной для поиска хорошо приближающих методов интерполяции. Интерполяционные полиномы, приводимые в литературе по численным методам, обычно применимы только к регулярной сетке интерполяции. Однако для решения различных инженерных задач, например, таких, как структурная разработка параболических рефлекторов для спутниковых антенн, исследователь должен пользоваться нерегулярной сеткой интерполяции для создания соответствующей модели рефлектора. Для того, чтобы провести интерполяцию для величин, находящихся внутри сетки нерегулярно расположенных узлов, необходимо иметь формулу интерполяции, подходящую для распределившихся таким образом узлов.
В общем случае, такая интерполяция используется для прямоугольной равномерной сетки (см. рис. ниже). Значение функции z=f(x,y) определено в узлах интерполяции (xi, yi) и интерполяция используется для определения значений функции z в других точках, не являющихся узлами.
Простой алгоритм нахождения значений, например, такой, как интерполяция многочленом Лагранжа, может быть использован для нахождения значений гладких непрерывных функций. Применительно к случаю, когда значения функции zii=f(xi, yi) определены в узлах интерполяции (xi, yi) регулярной сетки (i=0, …, I; j=0, …, J), и в этих точках существуют первые производные, т. е. определены zx(xi, yi) и zy(xi, yi), в ходе интерполяции происходит попытка максимально приблизить z=f(x, y) к гладкой функции, принимающей заданные значения в узлах интерполяционной сетки. В этом случае функция находится следующим образом:
,
где
;
M, N выбираются так, чтобы коэффициенты
могли быть найдены посредством решения полученных уравнений
zij, =0;
zx(xi,yj)=0;
zy(xi, yi)=0;
zxy(xi, yj)=0.
В том случае, когда M=N=3, функция z называется бикубической.
Область применения этого метода интерполяции ограничивается данными, расположенными регулярно, образующими прямоугольную сетку интерполяции.
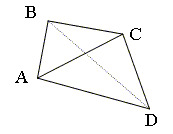
Для того чтобы получить функцию, пригодную для интерполяции нерегулярно расположенных исходных данных, вначале необходимо провести разбиение плоскости (x,y) на непересекающиеся треугольники с вершинами в опорных точках (триангуляцию), причем вершинами каждого из треугольников являются проекции на его плоскость узлов интерполяции; каждому треугольнику ставится в соответствие полином пятой степени от переменных x и y. Вычисляются значения частных производных в каждой исходной точке и затем используются для определения коэффициентов для полиномов, каждый из которых задается для своего треугольника. Значения переменной z вычисляются посредством этих полиномов, зависящих от x и y:
. (5)
Посредством подстановки в формулу (5) известных значений z в вершинах треугольника и частных производных zx, zy, zxx, zxy, zyy (это дает 18 линейно независимых уравнений) определяется 21 коэффициент {ajk}. Еще три уравнения можно получить, подставив значения частных производных z, взятых по направлениям, перпендикулярным каждой из трех сторон треугольника соответственно.
Весь процесс можно кратко описать следующим образом:
1) провести триангуляцию точек на плоскости x,y, считая их вершинами треугольников триангуляции;
2) найти частные производные z в каждой точке (xi, yi);
3) для точки (x, y), в которой ищется значение z(x, y) найти проекцию на плоскость x, y и треугольник, внутри которого эта проекция располагается;
4) исходя из заданных и найденных условий, используя формулу (5), вычислить искомое значение z(x, y).
Если узлы интерполяции расположены регулярно, можно воспользоваться интерполяционным многочленом Лагранжа (нет необходимости проводить триангуляцию в плоскости (x,y)).
Алгоритм триангуляции
Триангуляция Делоне - это разбиение нерегулярного множества опорных точек на такую сеть треугольников, когда система взаимосвязанных неперекрывающихся треугольников имеет наименьший диаметр, если ни одна из вершин не попадает внутрь ни одной из окружностей, описанных вокруг образованных треугольников [7].
Это означает, что образовавшиеся треугольники при такой триангуляции максимально приближаются к равносторонним, а каждая из сторон образовавшихся треугольников из противолежащей вершины видна под максимальным углом из всех возможных для точек соответствующей полуплоскости.
При создании алгоритма, автоматизирующего построение триангуляции Делоне, в качестве базового было выбрано свойство триангуляции Делоне давать локально наиболее правильные треугольники. Это позволило, во-первых, не бояться ошибок, связанных с машинными погрешностями, во-вторых, получить инкрементный алгоритм, то есть алгоритм, постепенно включающий точки в уже построенную триангуляцию и по определению позволяющий легко реагировать на ситуацию при появлении новых данных и, в-третьих, данный алгоритм работает за время, пропорциональное числу точек.
Ещё одним преимуществом этого алгоритма является простота удаления ранее внесённых и обработанных точек.
Благодаря возможности легко вносить и удалять точки из ранее построенной триангуляционной сетки, получается алгоритм, способный работать в режиме реального времени.
Одной из основных трудностей при использовании инкрементного алгоритма является проблема отыскания того треугольника, в который попала новая точка. Эта проблема решена следующим образом: вводится вспомогательная очень крупная прямоугольная сетка, в каждую из ячеек которой попадает некоторое число треугольников. Определив, к какой ячейке принадлежит новая точка, локализуются "подозрительные" треугольники. Проверяя принадлежность точки к этим треугольникам, либо получаем искомый номер, либо выясняется, что точка лежит вне уже построенной конструкции.
Обработка последнего случая вызывает некоторые трудности, требуется проверить каждую из внешних точек имеющейся триангуляции Делоне на возможность соединения с новой точкой, и последующего образования треугольника. Эта проблема решается путём исследования отрезка, соединяющего новую точку с рассматриваемой, на предмет пересечения его с каким-либо внешним из ребер имеющейся триангуляции Делоне. Пересечение (или его отсутствие) устанавливается изучением системы линейных уравнений, образованной уравнениями прямых, содержащих вышеупомянутые отрезки.
В случае попадания новой точки в треугольник, ранее построенной триангуляции, происходит ликвидация этого треугольника и появление трёх новых (на базе четырёх точек – новой и трёх вершин ликвидированного треугольника). Появившиеся треугольники исследуются на возможность построения флипов (флип - операция переброски диагонали выпуклого четырехугольника, т.е. если у четырехугольника ABCD, разбитого диагональю BD на два треугольника, удалить эту диагональ и заменить ее на AC, то получится другая триангуляция четырехугольника). Преобразованные после флипов треугольники добавляются в разряд исследуемых.
Выбор структуры для представления триангуляции оказывает существенное влияние на теоретическую трудоёмкость алгоритмов, а также на скорость конкретной реализации. Кроме того, выбор структуры может зависеть от цели дальнейшего использования триангуляции.
В триангуляции можно выделить три основных вида объектов: узлы (точки, вершины), рёбра (отрезки) и треугольники.
В работе используемого алгоритма построения триангуляции Делоне возникают следующие операции с объектами триангуляции:
1. Треугольник → узлы: получение для данного треугольника координат образующих его узлов.
2. Треугольник → рёбра: получение для данного треугольника списка образующих его рёбер.
3. Треугольник → треугольники: получение для данного треугольника списка соседних с ним треугольников.
4. Ребро → узлы: получение для данного ребра координат образующих его узлов.
5. Ребро → треугольники: получение для данного ребра списка соседних с ним треугольников.
6. Узел → рёбра: получение для данного узла списка смежных рёбер.
7. Узел → треугольники: получение для данного узла списка смежных треугольников.
В используемой структуре для каждого узла триангуляции хранятся его координаты на плоскости и список указателей на соседние узлы (список номеров узлов), с которыми есть общие рёбра. По сути, список соседей определяет в неявном виде рёбра триангуляции. Треугольники же при этом не представляются вообще, что является обычно существенным препятствием для дальнейшего применения триангуляции. Кроме того, недостатком является переменный размер структуры узла, зачастую приводящий к неэкономному расходу оперативной памяти при построении триангуляции.
Экспериментальные данные
Используемая экспериментальная установка устроена следующим образом: измерительные датчики линейно расположены на неподвижной планке, в то время как сферическая поверхность, служащая для фокусировки сигнала, совершает вращательно-поступательное движение вокруг оптической оси установки. Таким образом, геометрия получаемых экспериментальных данных имеет весьма нетривиальный характер. Все точки, в которых проводятся измерения, расположены на нескольких (порядка 10) сдвинутых относительно друг друга окружностях. Причем расстояние между соседними точками на одной окружности постоянно, как и расстояние между центрами соседних окружностей. Количество точек на одной окружности — порядка 500.
Плотность покрытия точками исследуемой области сильно зависит от соотношения диаметра окружностей и сдвига между ними. Также характерной особенностью является очень высокая плотность точек на окружностях и большие незаполненные области между ними.
Восстановление изображений
Поскольку все экспериментальные точки лежат на не слишком сложной кривой (на окружности), удобно перейти к одномерной задаче на этой кривой. Таким образом удастся максимально уточнить (восстановить) данные на окружностях.
Занумеруем все экспериментальные точки по порядку, сначала на первой окружности, потом на второй, и так далее. Точки, находящиеся на разных окружностях, будем обрабатывать отдельно. Численный эксперимент показал, что влияние сравнительно удаленных точек, находящихся на других окружностях, не очень велико, и им можно пренебречь. После восстановления значений на каждой окружности осуществляется интерполяция данных на прямоугольную сетку. Основные преимущества подобного подхода состоят в следующем:
во-первых, исходная двумерная задача сводится к решению набора одномерных задач, что гораздо проще с вычислительной точки зрения;
во-вторых, в случае неисправности одного из датчиков это не оказывает влияние на обработку данных с других датчиков;
в-третьих, решается проблема с нормировкой аппаратной функции, так как у каждой точки при таком подходе существует конечное число соседних точек на заранее известных расстояниях;
в-четвертых, возможно разделение задачи на несколько независимых задач по числу окружностей, что позволяет решать задачу с помощью параллельных вычислений на нескольких ЭВМ и получить многократный выигрыш в скорости.
Аппаратная функция каждой одномерной задачи фактически представляет собой квадратную симметричную матрицу
размера
. Заменим свертки по площади исходной области на одномерные суммы вида
(6).
Таким образом, формулы используемого алгоритма ISRA принимают вид:
.
Сходимость данного алгоритма может быть доказана методом проектирования на выпуклые множества [2].
Благодаря сохранению геометрии исходных данных возможно кэширование значительного количества вычисляемых величин: значений аппаратной функции для всех пар точек, расстояний между ними, расстояний между исходными и интерполяционными точками. Несмотря на значительный объем кэшируемых данных, обращение к ним может происходить последовательно, что в сочетании с большими размерами доступной памяти на современных компьютерах делает возможным ускорить процесс обработки изображения в десятки раз.
В целом процесс обработки экспериментальных данных выглядит следующим образом:
1. при необходимости осуществляется прореживание экспериментальных данных;
2. отдельно для каждой окружности реализуется алгоритм восстановления изображения (n-итераций);
3. оценивается качество полученного изображения, принимается решение о продолжении или завершении процесса;
4. восстановленные данные интерполируются на прямоугольную сетку;
5. полученное изображение сохраняется и демонстрируется на экране.
Результаты
Изучение сходимости алгоритма ISRA было проведено на примере одномерной задачи. Рассматривалась единичная окружность с экспериментальными точками. На модельных данных установлена сходимость алгоритма в норме L2.
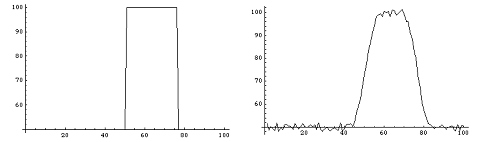
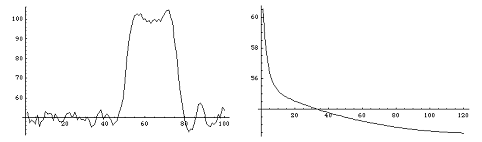
Ниже представлены графики исходного сигнала (график 1), сигнала после воздействия аппаратной функции и наложения шума (график 2), график восстановленного сигнала (график 3) и график разницы между исходным и восстанавливаемым сигналом на различных итерациях (график 4), то есть график зависимости нормы разности исходного и восстанавливаемого сигнала от номера итерации.
график 1
график 2
график 3
график 4
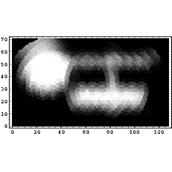
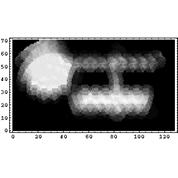
Восстановлению основного характера изображения (в данном случае: ширины и формы пика) сопутствует также усиление фонового шума. К сожалению, этот недостаток характерен для всех алгоритмов восстановления изображения, и для его устранения требуются дополнительные сведения о начальных данных.Кроме того, проведен ряд численных экспериментов с модельными данными для двумерного случая: имеет место сходимость итерационного процесса восстановления, а также визуальное повышение качества изображения. Ниже представлены примеры работы программы. Созданное вручную прямоугольное изображение (круг и три прямоугольника разных размеров) было размыто с помощью стандартной модельной аппаратной функции и интерполировано на окружности. Результат преобразования отображен на первом рисунке. Далее было проведено 100 итераций алгоритма ISRA. Результат восстановления показан на втором рисунке. Заметно повышение резкости контуров контрастных областей (особенно заметно для верхнего горизонтального прямоугольника).
модельное изображение
изображение после 100 итераций ISRA
Отдельно рассматривался вопрос о качестве восстановленного изображения в зависимости от геометрии расположения экспериментальных точек. Естественно, что оптимальным является наиболее равномерное покрытие области. На плохо покрытых экспериментальными точками частях области, например, вблизи границы, появляются значительные искажения. В то же время большая плотность точек на окружностях при малом количестве самих окружностей не улучшает качества восстанавливаемого изображения, а при использовании интерполяционных методов, основанных на триангуляции области, может приводить и к ухудшению качества восстановления. Этот вопрос рассматривался при обработке ряда экспериментальных данных.
Создана программа, осуществляющая восстановление и интерполяцию экспериментальных данных. Программа реализована на языке C и способна работать в любой UNIX-подобной операционной системе (тестирование проводилось на linux, mac os x). Реализованы 3 режима работы:
· режим генерации таблиц;
· нормальный режим;
· режим работы с модельными данными.
Для повышения производительности максимально возможное число вычислений перенесено на этап генерации таблиц, при этом формируется большой (порядка 100 мегабайт) кэшируемый массив данных, использующихся в дальнейшей работе. Это позволило вплотную приблизиться к требованию работы в реальном времени: для модельных данных (512 точек, 1000 итераций ISRA, inverse-distance weighted procedure, размер конечной сетки 128x128) время обработки данных составило менее секунды на компьютере PowerPC G4 (1.42 GHz, 512 Mb RAM).
Заключение
Разработка математических методов обработки радиометрических изображений позволяет частично компенсировать физические недостатки метода. Особенно актуальной является задача первичного анализа получаемых изображений: выделение контрастных областей, оконтуривание потенциальных предметов. Наложение изображений, получаемых радиометрическим и обычным (в видимом диапазоне) способом, особенно в реальном времени, позволяет решать задачи выявления скрытого под одеждой оружия и других предметов. Пассивный характер радиометрии позволяет сделать этот процесс внешне незаметным.
Развитие экспериментальной техники на базе Центра Магнитной Томографии МГУ, осуществляемое в настоящее время (создание многоканальных систем, повышение скорости сбора информации) создает необходимость в развитии соответствующих математических методов, позволяющих с небольшими временными затратами обрабатывать и визуализировать радиометрические изображения.
Литература
1. Пирогов Ю.А. Пассивное радиовидение в миллиметровом диапазонедлин волн // Известия вузов. Радиофизика. - 2003. - Том XLVI. №8-9. С.660-670.
2. Тимановский А.Л. Сверхразрешение в системах пассивного радиовидения // Диссертация на соискание ученой степени кандидата физ.-мат. наук.- М.: физич.ф-т МГУ, 2007.
3. Madisetti V.K., Williams D.B. The Digital Signal Processing Handbook.- CRC Press, 1999.
4. Lanteri H., Soummer R., and Aime C. Comparison between ISRA and RLA algorithms. Use of a Wiener Filter based stopping criterion // Astronomy & astrophysics supplement series, Vol. 14, 1999, pp. 235-246.
5. De Pierro A.R. On the Relation between the ISRA and the EM Algorithm for Positron Emission Tomography, 1993, IEEE. Trans. Med. Imaging, MI-12, 328-333.
6. Пирогов Ю.А., Гладун В.В., Тищенко Д.А., Тимановский А.Л., Шлемин И.В, Джен С.Ф., // Журнал радиоэлектроники (http://jre.cplire.ru), 2004, №3.
7. Скворцов А.В. Триангуляция Делоне и ее применение //ТГУ. 2002. С. 27-29.