UDC 517: 519.62: 535.4: 621.38
PACS numbers: 02.60.Nm, 03.65.Db, 03.65.Nk, 05.40.Ca, 42.82.-m
Analysis of the propagation, transformation and scattering of the monochromatic electromagnetic waves in the irregular waveguides: a case of integrated-optical waveguide with statistic surface roughness and a case of optical nanofibers with random rough surface
A.A. Egorov,1 A.V. Stavtsev,2 T.K. Chekhlova,2 A.G. Timakin,2 V.I. Grygoruk,3
Yu.A. Gayday,3 A.V. Kovalenko,3 V.N. Kurashov3
1A.M. Prokhorov General Physics Institute, Russian Academy of Sciences,
2 Peoples' Friendship University of Russia
3 Taras Shevchenko National University of Kyiv
Received September 9, 2010
Abstract. We examine in this paper two cases, which are very interested for the theory and experiments: a case of an integrated-optical waveguide with statistic surface roughness and a case of optical nanofibers with random rough surface. The peculiarities of approximate solutions of vector electrodynamic problems in the first cases in brief are discussed and useful evaluations of losses due to scattering also are given. Some results of research of radiation losses of optical nanofibers in assumption of Gaussian statistics of distorted glass/air interface are presented. In conclusion we mark a problem of synthesizing of an optical processor or/and optical sensor with high metrological parameters with allowance for the problem of light scattering in optical waveguides with surface roughness.
Keywords: integrated optics, fiber optics, Maxwell’s equations, vector electrodynamics’ problems, irregular waveguide, multilayer waveguide, optical nanofibers, boundary conditions, waveguide modes, statistic irregularities, TE and TM modes, leaky modes, waveguide scattering, radiation losses, optical sensor, computer modelling.
1. Introduction
A lot of papers are devoted to the analysis of propagation of an electromagnetic wave in a planar multilayer regular dielectric two-dimensional (2D) waveguides (see, for example, [1-8]). A number of methods (see for example references [1-13]) are used for an analysis of processes of propagation and transformation of (wave)guiding, quasi-guiding and leaking modes, accompanying an exchange of energy among modes and between modes with surroundings in irregular waveguides.
The integrated-optical waveguide is one of basic elements of the integrated optics and waveguide optoelectronics [2, 4, 6, 7, 9, 10]. In most cases waveguide serves as the basis for creation of the various optical integrated circuits [4]. In this connection the important direction in technology is the development of methods of creation of a waveguide with a low level of losses of the intensity of the directed mode on scattering by three-dimensional (3D) irregularities (boundaries roughness and/or heterogeneities of the waveguide layers; smooth irregularities) of the structure of a waveguide.
In the paper we study two interested cases: a case of an integrated-optical waveguide with statistic surface roughness and a case of optical nanofibers with random rough surface.
The light scattered in a waveguide can be registered [2-10, 12-37]: i) like radiated substrate-cover (substrate-air) radiation modes, and/or substrate radiation modes, or leaky modes, and as the radiation, scattered in the plane of a waveguide in the case of boundaries roughness and/or heterogeneities of the waveguide layers; ii) like diffracted and/or leaky waves in the case of smooth irregularities.
As a rule, when analysing the waveguide scattering one gives main attention to the solution of the direct scattering problem i.e. to the determination of the field's or to the intensity's characteristics of the coherent radiation scattered in the waveguide. The found scattering diagrams (patterns) then can be used for the solution of an inverse problem [28, 33, 34] by the known comparison method, when one tries by that or different way to achieve the coincidence, for example, by the least squares method (in rms sense) of the experimentally measured diagrams with the theoretically calculated one.
When neglecting polarizing effects the problem of waveguide 3D scattering is reduced to a solution of known 2D wave equation. Then we assume absence of the cross-correlation relations between all types of irregularities (roughness of the boundaries and/or heterogeneity of the layers of waveguide).
Progress in fiber optics technologies caused attention to the problem of radiation losses induced with a roughness of a waveguide surface [40]. The open surface of the waveguide core has a structure of frozen capillary wave. As formation of such structure results from equilibrium thermodynamics, it can not be eliminated by means of technology. Therefore, the roughness induced radiation losses are intrinsic in the waveguides with glass/air interface. These losses are considered to be critical when essential part of the light power is carried with an evanescent wave, particularly in photonic crystal waveguides [41, 42], and optical nanofibers [44, 45].
The waveguide scattering method is the most suited tool for the metrological control in the integrated optics since the determined characteristics and parameters of waveguide irregularities characterize the waveguide in a whole just as an integrated structure but not as the separated mediums used for its manufacture [14-22, 24, 25, 28, 33]. The important advantage of the waveguide scattering method is that it allows increasing sensitivity of measurements in ~ 102-103 on a comparison with methods of single light scattering, due to repeated in phase scattering of the light on researched statistical irregularities. Other advantage of this method is the possibility of the research of scattering in a broad band of the variation of values of the lateral sizes of irregularities, including the size about the light wavelength [28-34, 39].
2. Scattering of electromagnetic monochromatic waves in an integrated-optical waveguide with statistic irregularities. Main equations
The scattering problem of a directed waveguide mode in a planar dielectric waveguide containing stochastic irregularities can be solved with the help of the theory of perturbations [2, 18, 24, 25, 28, 31-34, 39].
Generally
for the description of an electromagnetic field ![]() in an irregular integrated-optical
waveguide (see fig. 1) one can use the following vector
equation:
in an irregular integrated-optical
waveguide (see fig. 1) one can use the following vector
equation:
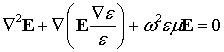 ,
(1)
,
(1)
where
![]() is
the electromagnetic field frequency;
is
the electromagnetic field frequency; ![]() ,
, ![]() ;
; ![]() and
and ![]() are the dielectric permittivity, and magnetic susceptibility, respectively;
are the dielectric permittivity, and magnetic susceptibility, respectively; ![]() and
and ![]() are the electric
and magnetic constants, respectively;
are the electric
and magnetic constants, respectively; ![]() is the
well-known vector differential operator, and
is the
well-known vector differential operator, and ![]() is Laplacian. This equation is fair in the
rectangular Cartesian coordinates. The equation (1) is found with the help of
the Maxwell’s equations.
is Laplacian. This equation is fair in the
rectangular Cartesian coordinates. The equation (1) is found with the help of
the Maxwell’s equations.
We consider the
case of propagation in a waveguide along ![]() -axis of the main TE-mode (for TM-mode the
analysis is carried out similarly). Next we can write equation (1) as the approximate three-dimensional
equation [28, 31-34, 39].
-axis of the main TE-mode (for TM-mode the
analysis is carried out similarly). Next we can write equation (1) as the approximate three-dimensional
equation [28, 31-34, 39].
Keeping in the obtained
equation only members of the first order of smallness in respect of ![]() and
and ![]() , we shall receive an approximate
inhomogeneous wave equation, which can be considered as a homogeneous wave
equation with perturbation as a source
, we shall receive an approximate
inhomogeneous wave equation, which can be considered as a homogeneous wave
equation with perturbation as a source ![]() in the right part:
in the right part:
![]() ,
(2)
,
(2)
where ![]() is
the solution of the homogeneous undisturbed equation circumscribing the
propagation of the main TE-mode in a waveguide forming of m-layers.
is
the solution of the homogeneous undisturbed equation circumscribing the
propagation of the main TE-mode in a waveguide forming of m-layers.
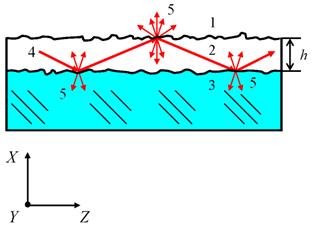
Fig. 1. A three-layer (m = 3)
irregular integrated-optical waveguide: 1 is the covering layer, 2 is the
guiding layer, 3 is the substrate, 4 is the optical ray, 5 is the light
scattered on the surface roughness; ![]() is the waveguide thickness. The optical ray 4 is propagating along the axes z, undergoing
the infringed total internal reflection on the rough boundaries of the
waveguide.
is the waveguide thickness. The optical ray 4 is propagating along the axes z, undergoing
the infringed total internal reflection on the rough boundaries of the
waveguide.
From the power point of view, the “source” in a right part of the equation (2) is the intensity of the mode, incident on an irregular area of waveguide and scattered in all enclosing space (3-D scattering).
The solution of the given inhomogeneous wave equation can be obtained
as a convolution of some Green function ![]() with the
expression for the source
with the
expression for the source ![]() :
:
![]() . (3)
. (3)
The analysis shows, that in this case it is impossible to neglect polarizing effects and the consideration of the problem of waveguide scattering of light on three-dimensional irregularities becomes hardly complicated, since the determination of analytical expression for a Green function represents here not at all trivial problem.
When neglecting the polarizing effects, originating during scattering, it is enough to require, that the relative variation of the dielectric permittivity on a distance of one wavelength was much less than unit. Then it is possible to use a simple wave equation:
![]() ,
(4)
,
(4)
which is fair for each Cartesian component of the vector of electrical
field. For fundamental TE-mode, propagating along the axes ![]() , under condition
, under condition ![]() = 0, the formula (4) accepts
next form:
= 0, the formula (4) accepts
next form:
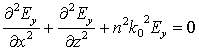 ,
(5)
,
(5)
where ![]() ,
,
![]() describes regular properties of an appropriate medium of waveguide
(accepts values
describes regular properties of an appropriate medium of waveguide
(accepts values ![]() ,
,
![]() or
or ![]() accordingly), and the
component
accordingly), and the
component ![]() describes irregularities of the structure of a waveguide
(both irregularity of the boundaries, and heterogeneity of a refraction index).
describes irregularities of the structure of a waveguide
(both irregularity of the boundaries, and heterogeneity of a refraction index).
For application of the theory of perturbations the addendum ![]() should
not be necessarily the value of the small order. There is quite enough, that
the area, within the limits of which this component differs from zero, was very
narrow. The solution of the equation (5) with help of the approximate method of
“ideal modes” [2] is then finding as the expansion of certain scattering
field on the orthogonal set of the modes of the rectilinear optical waveguide.
should
not be necessarily the value of the small order. There is quite enough, that
the area, within the limits of which this component differs from zero, was very
narrow. The solution of the equation (5) with help of the approximate method of
“ideal modes” [2] is then finding as the expansion of certain scattering
field on the orthogonal set of the modes of the rectilinear optical waveguide.
Thus the solution for component of a scattered field in any point of space with coordinates x, z takes form:
![]() , (6)
, (6)
where
![]() is
the effective amplitude of scattering TE-modes, defined as factor of expansion
of a field on all radiation modes;
is
the effective amplitude of scattering TE-modes, defined as factor of expansion
of a field on all radiation modes; ![]() is the transversal component of the
propagation constant of the radiation modes (see fig. 2).
is the transversal component of the
propagation constant of the radiation modes (see fig. 2).
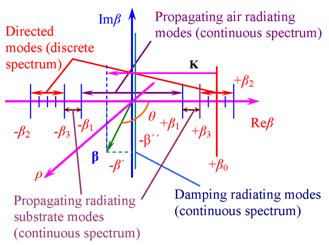
On the fig. 2 the diagram of the
wave numbers β and ρ are presented: ![]() , k = 2π/λ,
m = 1, 2, 3; K is a certain harmonic lattice vector in the
infinitive spectrum of the irregularities; θ is the scattering
angle in the xz plane of incidence. Here β represents the longitudinal component of the
propagating constant of radiating modes.
, k = 2π/λ,
m = 1, 2, 3; K is a certain harmonic lattice vector in the
infinitive spectrum of the irregularities; θ is the scattering
angle in the xz plane of incidence. Here β represents the longitudinal component of the
propagating constant of radiating modes.
The factors of expansion are fined from the orthogonality relations with the help of the theory of perturbations. Both numerical methods of direct calculation and analytical methods of determination of an approximate value of the integral in expression (6) can be used, for example, method of the stationary phase or saddle point method.
If the condition ![]() = 0 is executed, it is
possible to express any distribution of the field of a waveguide as the
superposition of orthogonal TE- and TM-modes of an ideal rectilinear waveguide
[2]:
= 0 is executed, it is
possible to express any distribution of the field of a waveguide as the
superposition of orthogonal TE- and TM-modes of an ideal rectilinear waveguide
[2]:
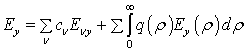 ,
,
where the first sum is distributed to all guided even and odd TE-modes, and the combination of the sum and integral takes into account all radiation modes.
Similarly for TM-modes:
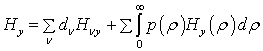 .
.
The expansion factors ![]() ,
, ![]() ,
, ![]() and
and ![]() are fined with the help of the
orthogonality relations.
are fined with the help of the
orthogonality relations.
Fig. 2. Wave numbers diagram of an asymmetric irregular optical waveguide
If the scattering happens on statistic irregularities, the averaging of the scattered radiation power on an ensemble is applied. Then the full intensity transferable in the waveguide or, for example, the power of the radiation stipulated by the scattering of the directed modes on the irregularities can be found. Thus, the solution of the direct scattering problem can be obtained as the field solution, i.e. as the peak-phase distributions, or as the solution circumscribing distribution of the intensity of the laser radiation scattered on irregularities. These expressions describe both the scattering on the irregularities of the boundaries of the waveguide and on the heterogeneities of the refraction index of the waveguide mediums.
To estimate the radiation losses of waveguide mode power due to waveguide scattering, we should find the full power, transferable by all propagating TE modes of an asymmetric irregular optical waveguide as follows:
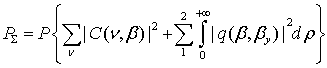 . (7)
. (7)
Our computer modeling according equation (7) demonstrates
e.g. that in an integrated-optical waveguide with the surface roughness
geometrical parameters ![]() = 4.2 nm (surface roughness rms high) and
= 4.2 nm (surface roughness rms high) and ![]() = 0.18 μm (surface
roughness correlation interval) the losses of the guided mode can achieve 6-10
dB/cm.
= 0.18 μm (surface
roughness correlation interval) the losses of the guided mode can achieve 6-10
dB/cm.
One can achieve some decrease of radiation losses in this
case by means of the certain optimization of parameters of the waveguide under
consideration, for example, by chosen of an optimal value of the longitudinal
component of the propagating constant ![]() of the guiding mode [39] (
of the guiding mode [39] (![]() is the effective refraction index of
the waveguide or an effective coefficient of waveguide phase slowing). We can
define needing
is the effective refraction index of
the waveguide or an effective coefficient of waveguide phase slowing). We can
define needing ![]() via resolving the dispersion
relation for investigating waveguide (see the next paragraph of this paper).
via resolving the dispersion
relation for investigating waveguide (see the next paragraph of this paper).
3. Dispersion relations and results of numerical calculations for three layer regular waveguide
For simulation the well known representation of dispersion relation in a trigonometrical kind for thee layer waveguide was used:
![]() ,
,
where ![]() is the vertical
component (for
is the vertical
component (for ![]() )
of the propagation constant of a directed ÒÅ-mode along an axes
)
of the propagation constant of a directed ÒÅ-mode along an axes ![]() ;
; ![]() is the thickness of a waveguide
layer;
is the thickness of a waveguide
layer; ![]() is the
factor of phase slowing down (effective waveguide refraction index);
is the
factor of phase slowing down (effective waveguide refraction index); ![]() is the vertical
component of the propagation constant of a directed ÒÅ-mode for
is the vertical
component of the propagation constant of a directed ÒÅ-mode for ![]() ;
; ![]() is the vertical component of the
propagation constant of a directed ÒÅ-mode for
is the vertical component of the
propagation constant of a directed ÒÅ-mode for ![]() ;
; ![]() = 0, 1, 2,….
= 0, 1, 2,….
The dispersing
relations ![]() for
the first five TE and ÒÌ modes of a regular three-layer polystyrene
integrated-optical waveguide are represented in the fig. 3.
for
the first five TE and ÒÌ modes of a regular three-layer polystyrene
integrated-optical waveguide are represented in the fig. 3.
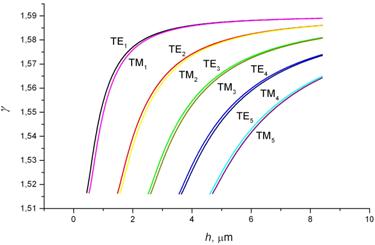
Fig. 3. Dispersing relation ![]() for three-layer polystyrene integrated-optical
waveguide.
for three-layer polystyrene integrated-optical
waveguide.
4. Optical nanofibers with random rough surface. Radiation losses in optical nanofibers with random rough surface
In recently published paper [46], the radiation losses in nanofibers are estimated in assumption of sinusoidally perturbed surface. It is demonstrated that for realistic perturbation amplitude, the typical values of the loss coefficient are about 1–10-3 dB/mm and substantially depend on the perturbation period and refractive index contrast. Besides, the paper contains the conclusion that the model of sinusoidal perturbation can be generalized for all kinds of the surface deformation by means of Fourier analysis. This statement is controversial because direct generalization of the represented model assumes linear relationship between the amplitude of perturbation and the power of light scattered by this perturbation.
Meanwhile, the radiated power is expressed as the square of linear functional of perturbation amplitude and thus can not be represented as a sum of independent contributions of perturbation’s Fourier components. This problem is solved with a help of statistical approach, when the perturbed surface is treated as a random field and the radiated power is determined with averaging over perturbation ensemble.
The statistical approach to the problem of light scattering in randomly perturbed waveguides, first developed in early studies of Marcuse [14, 48], was used in [41, 42] in order to estimate the lower bound of intrinsic losses in photonic crystal fibers. The mean radiated power is expressed through the power spectral density of the random roughness and this relation has the linear character. Marcuse’s approximation is quite good for weakly guiding fibers but it sets aside the following.
It is well known [49] that the solution of Maxwell equations for inhomogeneous medium in the first approximation of the small perturbation method has a form of linear relation between the mean power of the scattered wave and the power spectral density of refractive index fluctuations. It is demonstrated [48] that the perturbation of the waveguide surface can be represented with equivalent perturbation of the refractive index. The refractive index perturbation is expressed as discontinuous function of the amplitude of the surface roughness. As this relation can not be linearized, the radiated power must have nonlinear form of dependence on the roughness power spectrum even in the first approximation of the small perturbation method. This means that a part of the scattered power, proportional to low frequency components of the roughness spectrum, is lost in the linear solutions. As the power spectrum has inverse-square law of dependence on the spatial frequency [43], the scattering on harmonics of the small frequencies can be considerable.
It was established former [50] that the power spectrum of refractive index fluctuations in perturbed planar waveguide can be expressed through the roughness correlation with a help of Price’s theorem about nonlinear operations over Gaussian random field [51, 52]. In the present paper, we establish the relation between the radiation losses and the power spectrum of the rough surface of nanofiber, and to estimate the loss value.
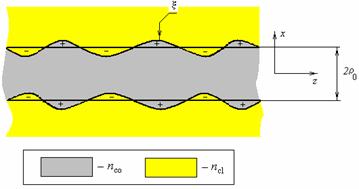
Following [6, 40,
46], the rough surface of a fiber waveguide
(fig. 4) is represented as a variation of its radius ![]() :
:
![]() . (8)
. (8)
In equation (8) ![]() is the radius of unperturbed waveguide, the function
is the radius of unperturbed waveguide, the function ![]() describes the perturbation (see fig. 4).
describes the perturbation (see fig. 4).
We take that ![]() is the uniform Gaussian random field [12]
with zero mean and statistical correlation function, which depends on the
residual coordinates
is the uniform Gaussian random field [12]
with zero mean and statistical correlation function, which depends on the
residual coordinates ![]() ,
,
![]() :
:
![]() ,
,
where ![]() is the roughness variance,
is the roughness variance, ![]() denotes normalized
correlation. We suppose the perturbation magnitude
denotes normalized
correlation. We suppose the perturbation magnitude ![]() being small. The small order of
being small. The small order of ![]() means that the
amplitude of electric field of both propagating and radiation modes can be
considered constant within the perturbed region. As in nanofibers the
perturbation is less in scale than 1 nm [44], the small order condition holds with high
accuracy.
means that the
amplitude of electric field of both propagating and radiation modes can be
considered constant within the perturbed region. As in nanofibers the
perturbation is less in scale than 1 nm [44], the small order condition holds with high
accuracy.
We confine the consideration to the most important case of
single-mode operation of the waveguide. So, the propagating light wave has the
appearance of the fundamental HE11 mode with electric component ![]() .
.
The scattered wave is expressed as a superposition of radiation ITE and ITM modes:
![]() ,
,
where ![]() , the signs “+/-”correspond to the forward and
backward propagating modes, respectively, and:
, the signs “+/-”correspond to the forward and
backward propagating modes, respectively, and:
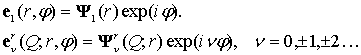
The total mean power, radiated with the random roughness, is expressed with integral over the whole of system of radiation modes [14, 40, 48].
The loss coefficient is obtained as:
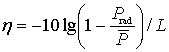 . (9)
. (9)
In equation (9) ![]() is the power of the fundamental mode;
is the power of the fundamental mode; ![]() is the length of fiber. It follows from our results
that radiation losses are linear in
is the length of fiber. It follows from our results
that radiation losses are linear in ![]() .
.
We applied the proposed theoretical model to estimate the
radiation losses caused with the rough glass/air interface of the nanofibers.
The physical parameters of the model were chosen so as to make possible
comparison with the reported experiments [44, 45]. For the lack of data, we
confined the calculation to the case of the silica fiber, for which we accepted ![]() = 1.46.
= 1.46.
Fig. 4. Perturbed fiber waveguide. nco, ncl, are the refractive indices of the core and the cladding (air), respectively.
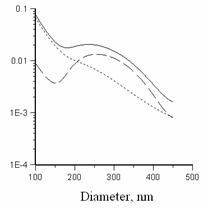
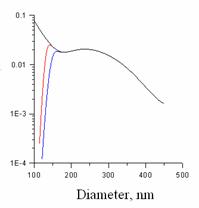
The dependence of the loss coefficient on the fiber diameter
was calculated for the wavelength ![]() = 633 nm (see fig. 5).
= 633 nm (see fig. 5).
We should note that the perturbation power spectrum is expected to have inverse-square low, therefore, the contribution of the low frequencies is very critical, and could be explained in terms of the effective depth of the perturbed layer.
Note that passage to the limit of spatial frequencies ![]() 0 gives the reasonable estimation of losses, but
leads to the growth of the effective depth of the perturbation to the values
which exceed the waveguide diameter. To our opinion, the extremely low
frequency perturbations with large amplitudes should be understood as random
waveguide bends. Naturally, there are no reasons to describe such perturbations
with the inverse-square law spectrum. So, the estimation of radiation losses in
the silica nanofibers with
0 gives the reasonable estimation of losses, but
leads to the growth of the effective depth of the perturbation to the values
which exceed the waveguide diameter. To our opinion, the extremely low
frequency perturbations with large amplitudes should be understood as random
waveguide bends. Naturally, there are no reasons to describe such perturbations
with the inverse-square law spectrum. So, the estimation of radiation losses in
the silica nanofibers with ![]() 180 nm has rather qualitative character.
180 nm has rather qualitative character.
|
a)
|
b)
|
Fig. 5. Dependence of the loss coefficient on the fiber diameter, in dB/mm.
a) Linear approximation (dash), nonlinear loss component (dot), aggregate losses (solid), bcut = 0. b) Losses for different cutoff frequencies of surface perturbation, bcut = 1.0 mm-1 (blue), bcut = 0.1 mm-1 (red), bcut = 0 (black).
The calculated losses are somewhat less in value than those observed experimentally. Apparently, the suggested model is approximate, and sets aside some important particularities of the experiment. With it, the model must be useful in understanding of losses in optical nanofibers, caused with intrinsic roughness of glass/air interface.
5. Conclusion
All facts following from the presented paper should be taken into consideration, when one needs to synthesize e.g. an optical processor or/and optical sensor with high metrological parameters [4, 7, 9, 12, 13, 37-40, 44, 53-58].
In summary we should noted that the offered methods can be applicable for analysis of similar dielectric, magnetic, optic and meta materials structures in enough broad band of electromagnetic wavelengths.
References
1. Derugin L.N., Marchuk A.N., Sotin V.E. Properties of flat asymmetrical dielectric waveguides on a substrate from a dielectric // Izvestiia Vuzov Radioelectronika. 1967. V. 10. No. 3. pp. 134-141.
2. Marcuse D. Light transmission optics. New York: Van Nostrand, 1972.
3. Katsenelenbaum B.Z. The theory of irregular waveguides with slowly changed parameters. Moscow: Izdatelstvo USSR’ Academy of Sciences, 1961.
4. Hunsperger R.G. Integrated Optics: Theory and technology. New York: Springer-Verlag, 1984.
5. Shevchenko V.V. Smooth transitions in open waveguides (Introduction in the theory). Moscow: Nauka, 1969.
6. Snyder A.W., Love J.D. Optical waveguide theory. London: Chapman and Hall, 1983.
7. Integrated Optics / Ed. By Tamir T. New York.: Springer-Verlag. 1975.
8. Sodha M.S., Ghatak A.K. Inhomogeneous optical waveguides. London.: Plenum Press. 1977.
9. Southwell W.H. Inhomogeneous optical waveguide lens analysis // JOSA. – 1977. V. 67. No. 8. pp. 1004-1009.
10. Sevastianov L.A, Egorov A.A. The theoretical analysis of waveguide propagation of electromagnetic waves in dielectric smoothly-irregular integrated structures. // Optics and Spectroscopy. 2008. V. 105, No. 4. pp. 576-584.
11. Babich V.M., Bulderev V.S. Asymptotic methods in problems of diffraction of short waves. Moscow: Nauka, 1972.
12. Egorov A.A., Sevastyanov L.A., Sevastyanov A.L. Iinvestigation of electrodynamic properties of planar thin-film Luneberg's lens // Journal of Radio Electronics. 2008. No. 6. pp. 1-20.
13. Egorov A.A., Sevast'yanov L.A. Structure of modes of a smoothly irregular integrated-optical four-layer three-dimensional waveguide // Quantum Electronics. 2009. V. 39. No. 6. pp. 566-574.
14. Marcuse D. Radiation losses of dielectric waveguides in terms or the power spectrum or the wall distortion function // Bell System Tech. J. 1969. V. 48. No. 10. pp. 3233-3242.
15. Suematsu Y., Furuya K. Propagation mode and scattering loss of a two dimensional dielectric waveguide with gradual distribution of refractive index // IEEE Trans. on MTT. 1972. V. 20. No. 7. pp. 524-531.
16. Tsai T.L., Tuan H.S. Reflection and scattering by a single groove in integrated optics // IEEE J. of QE. 1974. V. 10. No. 3. pp. 326-332.
17. Miyanaga S., Imai M., Asakura T. Radiation pattern of light scattering from the core region of dielectric-slab-optical waveguides // IEEE J. of QE. 1978. V. 14. No. 1. pp. 30-37.
18. Walter D.J., Houghton J. Attenuation in thin film optical waveguides due to roughness-induced mode coupling // Thin Solid Film. 1978. V. 52. pp. 461-476.
19. Hall D.G. Scattering of optical guide waves by waveguide surface roughness: a three-dimensional treatment // Optics Letters. 1981. V. 6. No. 12. pp. 601-603.
20. Andler G., Egorov A.A., Cheremiskin I.V. Determination of parameters of a roughness of an optical surface by the scattering in a dielectric waveguide // Optics and Spectroscopy. 1984. V. 56. No. 4. pp. 731-735.
21. Imai M., Ohtsuka Y., Haneda N. Out-of-plane scattering from ion exchanged optical waveguides // J. of Appl. Physics. 1985. V. 57. No. 11. pp. 4879-4882.
22. Hall D.G. In-plane scattering in planar optical waveguides: refractive-index fluctuations and surface roughness // JOSA. A. 1985. V. 2. No. 5. pp. 747-752.
23. Juk N.P. Eigen waves of an average field in a statistically irregular planar waveguide // Jurnal Tehnicheskoi Fiziki. 1986. V. 56. No. 5. pp. 825-830.
24. Siro F. Vaskez S. de F., Egorov A.A., Cheremiskin I.V. To a problem on determination of statistical characteristics of irregularities of thin-film wave guides // Optoelectronics, Instrumentation and Data Processing. 1991. No. 2. pp. 51-55.
25. Egorov A.A. Characteristics of a radiation, scattered on roughness of a surface of a substrate of a planar waveguide // Surface. Physics, chemistry, mechanics // 1994. No. 5. pp. 72-76.
26. Egorov A.A. Theory of waveguide optical microscopy // Laser Physics. 1998. V. 8. No. 2. pp. 536-540.
27. Paulus M., Martin Oliver J.F. A fully vectorial technique for scattering and propagation in three-dimensional stratified photonic structures // Optical and QE. 2001. V. 33. pp. 315-325.
28. Yegorov A.A. A new algorithm of restoring the autocorrelation function of subwavelength statistic surface roughness by light scattering in integrated optical waveguide in the presence of a high additive stochastic noise // Proc. SPIE. 2002. V. 4900. pp. 792-801.
29. Egorov A.A. Vector theory of the waveguide scattering of laser radiation in the presence of noise (method of modes and method of Green’s function) // Laser Physics. 2004. V. 14. No. 8. pp. 1072-1080.
30. Egorov A.A. Theory of waveguide light scattering in an integrated optical waveguide in the presence of noise // Radiophysics and Quantum Electronics. 2005. V. 48, No. 1. pp. 57-67.
31. Egorov A.A. Use of Wiener-Paley transform for processing of waveguide far-zone light scattering data // ICO Topical Meeting on Optoinformatics/Information Photonics 2006. September 4-7 2006. St. Petersburg. Russia. St. Petersburg: ITMO. pp. 234-235.
32. Egorov A.A. 3D Waveguide light scattering. Rigorous and approximate analysis // ICO Topical Meeting on Optoinformatics/Information Photonics 2006. September 4-7 2006. St. Petersburg. Russia. St. Petersburg: ITMO. pp. 371-372.
33. Egorov A.A. Inverse problem of scattering of monochromatic light in a statistically irregular waveguide: theory and numerical simulation // Optics and Spectroscopy. 2007. V. 103. No. 4. pp. 638-645.
34. Egorov A.A. Theoretical research of a correctness of an inverse problem of waveguide scattering of a laser radiation in a statistically irregular integrated-optical waveguide in absence of a noise // Journal of Radio Electronics. 2009. No. 4. pp. 1-20.
35. Egorov A.A., Sevastyanov A.L., Lovetskiy K.P. Zero approximation model of integrated-optical generalized Luneburg lens // Bulletin of PFUR. Ser. Mathematics. Computer science. Physics. 2009. No. 3. pp. 55-64.
36. Egorov A.A., Stavtsev A.V. Development and research of a complex of programs for calculation of main characteristics of integrated-optical waveguides in a system of visual programming Delphi and Ñ++ // Journal of Radio Electronics. 2009. No. 8. pp. 1-20.
37. Egorov A.A., Stavtsev A.V. Specifics of the development of algorithms and programs for computing the main characteristics of integrated-optical waveguides // Numerical Methods and Programming. 2010. V. 11. pp. 184-192.
38. Egorov A.A., Lovetskiy K.P., Sevastyanov A.L., Sevastianov L.A. Modelling of directed (eigen) modes and synthesis of thin-film generalized waveguide Luneburg lens in zero vectorial approximation integrated-optical // Quantum Electronics. 2010. (in press).
39. Egorov A.A. Use of waveguide light scattering for precision measurements of the statistic parameters of irregularities of integrated optical waveguide materials // Opt. Engineering. 2005. V. 44. pp. 014601-1–014601-10.
40. Kovalenko A.V., Kurashov V.N., Kisil A.V. Radiation losses in optical nanofibers with random rough surface // Optics Express. 2008. V.16. Iss.8, pp. 5797-5806.
41. Roberts P.J., Couny F., Sabert H., Mangan B.J., Williams D.P., Farr L., Mason M.W., Tomlinson A., Birks T.A., Knight J.C., Russell P.St.J. Ultimate low loss of hollow-core photonic crystal fibers // Opt. Express. 2005. V. 13. pp. 236-244.
42. Roberts P.J., Couny F., Sabert H., Mangan B.J., Birks T.A., Knight J.C., Russell P.St.J. Loss in solid-core photonic crystal fibers due to interface roughness scattering // Opt. Express. 2005. V. 13. pp. 7779-7793.
43. Jäckle J., Kawasaki K. Intrinsic roughness of glass surfaces // J. Phys.: Condens. Matter. 1995. V. 7. pp. 4351-4358.
44. Tong L., Gattass R.R., Ashcom J.B., He S., Lou J., Shen M., Maxwell I., Mazur E. Subwavelength diameter silica wires for low-loss optical wave guiding // Nature. 2003. V. 426. pp. 816-819.
45. Tong L.M., Hu L.L., Zhang J.J., Qiu J.R., Yang Q., Lou J.Y., Shen Y.H., He J.L., Ye Z.Z. Photonic nanowires directly drawn from bulk glasses // Opt. Express. 2006. V. 14. pp. 82-87.
46. Zhai Gaoye, Tong Limin. Roughness-induced radiation losses in optical micro or nanofibers // Opt. Express. 2007. V. 15. pp. 13805-13816.
47. Marcuse D. Theory of dielectric optical waveguides. New York: Academic Press, 1974.
48. Mandel L., Wolf E. Optical coherence and quantum optics. Cambridge: Cambridge Univ. Press, 1995.
49. Barchuk O.I., Kovalenko A.V., Kurashov V.N., Maschenko A.I. Statistical characteristics of fluctuations of dielectric constant in planar waveguide with rough walls // Ukrainskiy Fizicheskiy Zhurnal (Ukrainian Physical Journal). 1991. V. 36. pp. 612-617.
50. Price R. A Useful theorem for non-linear devices having Gaussian inputs // IEEE Trans. Inf. Theory. 1958. V. 4. pp. 69-72.
51. Papoulis A. Probability, Random Variables, and Stochastic Processes. New York: McGraw-Hill, 1984.
52. Tong L., Lou J., Mazur E. Single-mode guiding properties of subwavelength-diameter silica and silicon wire waveguides // Opt. Express. 2004. V. 12. pp. 1025-1035.
53. Lambeck P.V. Integrated opto-chemical sensors // Sensors and Actuators, 1992, V. 8, pp. 103-116.
54. Whitenett G., Stewart G., Atherton K., Culshaw B., and Johnstone W. Optical fibre instrumentation for environmental monitoring applications // J. Opt. A: Pure Appl. Opt., 2003, V. 5, pp. S140-S145.
55. Egorov A.A., Egorov M.A., Tsareva Yu.I., and Chekhlova T.K. Study of the integrated-optical concentration sensor for gaseous substances // Laser Physics, 2007, V. 17, pp. 50-53.
56. Egorov A.A., Egorov M.A., Chekhlova T.K., Timakin A.G. Low-loss inexpensive integrated-optical waveguides as a sensitive gas sensor // ICO Topical Meeting on Optoinformatics/Information Photonics 2008. September 15-18, 2008. St. Petersburg. Russia. St. Petersburg: ITMO. P. 208-211.
57. Egorov A.A., Egorov M.A., Chekhlova T.K., Timakin A.G. Study of a computer-controlled integrated optical gas-concentration sensor // Quantum Electronics. 2008. V. 38. pp. 787-790.
58. Cardenas J., Poitras C.B., Robinson J.T., Preston K., Chen L., Lipson M. Low loss etchless silicon photonic waveguides // Optics Express. 2009. V. 17. 4752-4757.