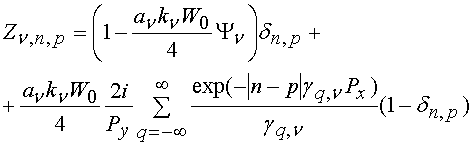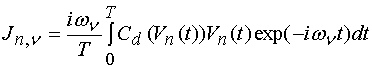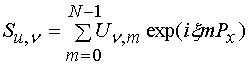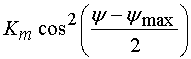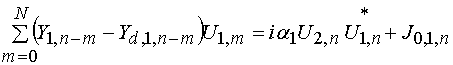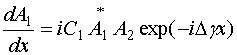УДК 621.396.67
ВЗАИМОДЕЙСТВИЕ ПРЯМОЙ И ОБРАТНОЙ ВОЛН В НЕЛИНЕЙНОМ ЭЛЕКТРОМАГНИТНОМ КРИСТАЛЛЕ
С. Е. Банков 1, М. Д. Дупленкова 2
1 ИРЭ им. В.А. Котельникова РАН, 2 ОКБ МЭИ
Получена 6 сентября 2011 г.
Аннотация. Численно исследовано взаимодействие электромагнитных волн, распространяющихся на первой и второй гармониках основной частоты в двумерном электромагнитном кристалле с нелинейными емкостями. Исследуется режим пространственного синхронизма прямой волны на основной частоте и обратной волны на второй гармонике. Изучены эффекты генерации второй гармоники основной частоты и параметрического усиления. Приводятся результаты численных экспериментов. Построена приближенная модель нелинейного электромагнитного кристалла в виде системы дифференциальных уравнений, описывающая двухчастотное взаимодействие прямой и обратной волн в режиме их пространственного синхронизма. Изучено решение в виде собственной волны. Получены аналитические выражения для напряжений на нелинейных элементах в режимах генерации второй гармоники и параметрического усиления.
Ключевые слова: электромагнитный кристалл, нелинейный электромагнитный кристалл, пространственный синхронизм, обратная волна, генерация второй гармоники, параметрическое усиление.
Abstarct. Interaction of waves propagating in electromagnetic crystal with non-linear capacitors at the first and second harmonics of the dominant frequency is considered. Regime of spatial synchronism of forward and backward waves at the first and second harmonics is investigated. Effects of second harmonic generation and parametrical amplification are numerically studied. Results of numerical experiments are presented. Analytical model describing waves interaction in regime of spatial synchronism is developed. Solution in form of eigen mode is studied. Analytical expressions for voltages at non-linear elements are obtained for regimes of second harmonic generation and parametrical amplification.
Keywords: electromagnetic crystal, non-linear electromagnetic crystal, spatial synchronism, backward wave, second harmonic generation, parametrical amplification.
1. Постановка задачи
Данная работа посвящена
исследованию взаимодействия электромагнитных волн в нелинейных периодических
структурах СВЧ диапазона, получивших название электромагнитных кристаллов
(ЭМК). Известно несколько видов таких взаимодействий [1]. Особый интерес
представляют явления, происходящие в условиях пространственного синхронизма
волн ЭМК, распространяющихся на разных гармониках основной частоты ![]() . Мы рассматриваем установившиеся
периодические процессы, в которых зависимость всех электрических параметров от
времени может быть описана суммой гармоник вида
. Мы рассматриваем установившиеся
периодические процессы, в которых зависимость всех электрических параметров от
времени может быть описана суммой гармоник вида ![]() . Здесь
. Здесь
![]() - круговая частота,
- круговая частота, ![]() - номер гармоники,
который принимает положительные и отрицательные значения. Основная частота
- номер гармоники,
который принимает положительные и отрицательные значения. Основная частота ![]() задается источником, возбуждающим ЭМК.
задается источником, возбуждающим ЭМК.
Следует отметить, что типичной для ЭМК, а также для фотонных кристаллов ситуацией является слабая нелинейность отдельного элемента. Поэтому сильные эффекты в таких структурах могут возникать только как результат когерентного сложения множества слабых нелинейных взаимодействий. Указанное выше когерентное сложение возникает при выполнении условий пространственного синхронизма.
В теории волн в нелинейных средах известен пространственный синхронизм сонаправленных волн [2]. Он возникает при выполнении следующего условия:
где ![]() -
целые числа, имеющие смысл номеров гармоник основной частоты
-
целые числа, имеющие смысл номеров гармоник основной частоты ![]() ,
, ![]() -
коэффициент замедления волны в среде,
-
коэффициент замедления волны в среде, ![]() - ее
постоянная распространения,
- ее
постоянная распространения, ![]() - волновое число
свободного пространства.
- волновое число
свободного пространства.
Термин сонаправленные волны
показывает, что речь идет о волнах, имеющих вектора Пойнтинга и волновые
вектора, ориентированные в одном направлении. Синхронизм сонаправленных волн
приводит к интенсивной связи волн на частотах ![]() и
и ![]() , которая может приводить, например, к
полной перекачке энергии с основной частоты на кратную ей частоту.
, которая может приводить, например, к
полной перекачке энергии с основной частоты на кратную ей частоту.
Особенностью периодических структур является возможность распространения в них обратных волн [3], у которых вектор Пойнтинга и волновой вектор направлены в противоположные стороны. В более сложных ситуациях, когда структура обладает анизотропией, указанные вектора могут быть ориентированы под некоторым углом. В рамках данной работы мы ограничимся анализом изотропных структур.
Существование обратных волн порождает новый вид пространственного синхронизма, который не возникает в непрерывных средах: синхронизм противонаправленных волн [4]. Под противонаправленными волнами мы понимает волны, у которых вектора Пойнтинга сонаправлены, а волновые вектора противонаправлены. Очевидно, что в этом случае одна из волн является прямой, а другая обратной. Условие синхронизма двух волн по-прежнему описывается уравнением (1). Однако физический его смысл существенно меняется, так как в отличие от случая двух прямых волн теперь энергии взаимодействующих волн распространяются в противоположных направлениях.
Отметим, что синхронизм противонаправленных волн является эффектом характерным исключительно для ЭМК. Возможность аномального поведения электромагнитных волн при выполнении условия (1) отмечалась в работе [4]. Однако, его качественные и количественные закономерности до сих пор практически не исследованы. Их изучению посвящена настоящая работа.
Она логически разделяется на две большие части. В первой части представлены результаты численного исследования ЭМК с помощью математической модели развитой в работе [5]. Указанная модель имеет вид системы нелинейных уравнений. Во второй части предложено аналитическое описание процесса распространения волн ЭМК в наиболее интересном режиме пространственного синхронизма. Для этого исходная математическая модель преобразуется к системе нелинейных дифференциальных уравнений, которая затем приближенно решается для ряда частных случаев.
2. Математическая модель ЭМК
Исследуемая структура показана на рис. 1. Она
представляет собой два металлических экрана, образующих плоский волновод (ПВ).
Внутри ПВ расположена решетка металлических цилиндров радиуса ![]() . В общем случае она имеет бесконечные
размеры по оси 0у и конечные размеры по оси 0х. Размеры решетки по этой оси
задаются числом
. В общем случае она имеет бесконечные
размеры по оси 0у и конечные размеры по оси 0х. Размеры решетки по этой оси
задаются числом ![]() . В цилиндры включены
сосредоточенные нелинейные емкости. Решетка, формирующая ЭМК, возбуждается
плоской волной, падающей под углом падения
. В цилиндры включены
сосредоточенные нелинейные емкости. Решетка, формирующая ЭМК, возбуждается
плоской волной, падающей под углом падения ![]() на
основной частоте
на
основной частоте ![]() .
.
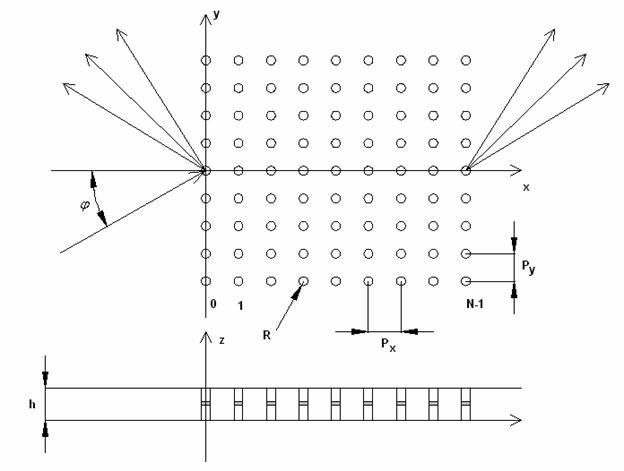
Рис. 1. Исследуемая структура.
Модель представленной выше структуры получена в работе [5]. Поэтому мы не будем подробно рассматривать вывод уравнений, к которым сводится граничная задача для электромагнитного поля, а приведем основные соотношения без вывода:
![]() ,
(2)
,
(2)
![]() ,
,
где
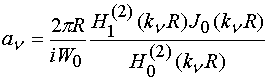 ,
,
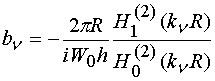 ,
,
![]() ,
,
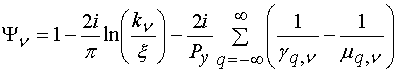 ,
,
![]() ,
, ![]() ,
,
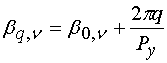 ,
,
![]() ,
, ![]() ,
,
где ![]() -
символ Кронекера,
-
символ Кронекера, ![]() - волновое сопротивление среды
внутри ПВ,
- волновое сопротивление среды
внутри ПВ, ![]() - волновое число свободного пространства
на частоте
- волновое число свободного пространства
на частоте ![]() ,
, ![]() -
высота ПВ,
-
высота ПВ, ![]() - периоды решетки ЭМК,
- периоды решетки ЭМК, ![]() - номер максимальной гармоники основной
частоты, учитываемой в решении,
- номер максимальной гармоники основной
частоты, учитываемой в решении, ![]() - номер гармоники
основной частоты. Индексы
- номер гармоники
основной частоты. Индексы ![]() описывают положение
элемента ЭМК по оси 0х. Вектора
описывают положение
элемента ЭМК по оси 0х. Вектора ![]() и
и ![]() имеют размерность равную
имеют размерность равную ![]() . Их элементами соответственно являются
токи, текущие по цилиндрам ЭМК и напряжения на нелинейных емкостях. Вектор
. Их элементами соответственно являются
токи, текущие по цилиндрам ЭМК и напряжения на нелинейных емкостях. Вектор ![]() имеет такую же размерность, а его
элементами являются напряженности компоненты поля
имеет такую же размерность, а его
элементами являются напряженности компоненты поля ![]() падающей
волны в центрах цилиндров ЭМК. При выводе соотношений (2) – (3) принято во
внимание, что в силу периодичности ЭМК по оси 0у все электродинамические
параметры имеют экспоненциальную зависимость от индекса
падающей
волны в центрах цилиндров ЭМК. При выводе соотношений (2) – (3) принято во
внимание, что в силу периодичности ЭМК по оси 0у все электродинамические
параметры имеют экспоненциальную зависимость от индекса ![]() :
:
![]() .
.
Индекс ![]() описывает
положение центра элемента ЭМК по оси 0у. Волновое число
описывает
положение центра элемента ЭМК по оси 0у. Волновое число ![]() задается
падающей волной, поле которой описывается следующим образом:
задается
падающей волной, поле которой описывается следующим образом:
![]() ,
,
![]() -
амплитуда электрического поля падающей волны.
-
амплитуда электрического поля падающей волны.
В уравнении (1) под ![]() понимается нелинейный оператор, связывающий гармоники тока с гармониками
напряжения на нелинейных емкостях. В общем случае он имеет следующий вид:
понимается нелинейный оператор, связывающий гармоники тока с гармониками
напряжения на нелинейных емкостях. В общем случае он имеет следующий вид:
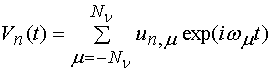 .
.
В формуле (5) индекс ![]() - это номер элемента ЭМК, задающий его
положение на оси 0х,
- это номер элемента ЭМК, задающий его
положение на оси 0х, ![]() - нелинейная емкость, зависящая
от напряжения
- нелинейная емкость, зависящая
от напряжения ![]() .
.
Благодаря оператору ![]() система уравнений (2) становится
нелинейной системой, которую в общем случае можно решить только численными
методами.
система уравнений (2) становится
нелинейной системой, которую в общем случае можно решить только численными
методами.
3. Собственные волны линейного ЭМК. Существование пространственного синхронизма.
До сих пор мы только предполагали, что пространственный синхронизм противонаправленных волн возможен. В данном разделе мы найдем параметры ЭМК частного вида (см. рис. 1), при которых этот режим взаимодействия волн действительно существует, и далее рассмотрим, как в нем ведут себя различные параметры ЭМК.
В качестве первого шага изучим поведение коэффициента замедления основной волны линейного ЭМК. Для этого временно допустим, что емкости, включенные в металлические цилиндры, не зависят от напряжений на них. Постоянные распространения собственных волн ЭМК находятся из решения следующего уравнения:
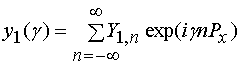 .
.
Если в ЭМК
отсутствуют диссипативные потери, то в силу четности функции ![]() уравнение (6) имеет корни симметрично
расположенные на комплексной плоскости
уравнение (6) имеет корни симметрично
расположенные на комплексной плоскости ![]() относительно
начала координат. Они могут быть либо действительными числами, либо мнимыми. В
этом случае вопрос о характере волны не имеет однозначного ответа. Мы не можем
утверждать, соответствует ли действительный корень прямой или обратной волне.
Поэтому для решения этой задачи нам необходимо ввести в структуру малые
диссипативные потери. Тогда все корни уравнения (6) становятся комплексными
числами. и для классификации волн мы можем воспользоваться правилом,
сформулированным в работе [6].
относительно
начала координат. Они могут быть либо действительными числами, либо мнимыми. В
этом случае вопрос о характере волны не имеет однозначного ответа. Мы не можем
утверждать, соответствует ли действительный корень прямой или обратной волне.
Поэтому для решения этой задачи нам необходимо ввести в структуру малые
диссипативные потери. Тогда все корни уравнения (6) становятся комплексными
числами. и для классификации волн мы можем воспользоваться правилом,
сформулированным в работе [6].
Волны
разделяются на прямые и встречные по знаку мнимой части постоянной ![]() . Прямые волны имеют
. Прямые волны имеют ![]() , а встречные
, а встречные ![]() . Таким
образом, этот признак разделяет волны на затухающие в положительном направлении
оси 0х (прямые волны) и в отрицательном (встречные волны). Их вектор Пойнтинга
ориентирован в направлении затухания волны. Также волны разделяются на прямые и
обратные. Прямые волны имеют
. Таким
образом, этот признак разделяет волны на затухающие в положительном направлении
оси 0х (прямые волны) и в отрицательном (встречные волны). Их вектор Пойнтинга
ориентирован в направлении затухания волны. Также волны разделяются на прямые и
обратные. Прямые волны имеют ![]() при
при ![]() и
и ![]() при
при ![]() . Инвертированные соотношения для
. Инвертированные соотношения для ![]() соответствуют обратным волнам. Мы можем
сделать вывод, что прямые волны имеют волновой вектор направленный вдоль
вектора Пойнтинга, а обратные в противоположную сторону. Таким образом,
например, под прямой прямой волной понимается волна у которой оба вектора
направлены в положительном направлении относительно оси 0х.
соответствуют обратным волнам. Мы можем
сделать вывод, что прямые волны имеют волновой вектор направленный вдоль
вектора Пойнтинга, а обратные в противоположную сторону. Таким образом,
например, под прямой прямой волной понимается волна у которой оба вектора
направлены в положительном направлении относительно оси 0х.
Далее,
говоря о параметрах собственной волны, мы будем иметь ввиду прямую в
энергетическом смысле волну, то есть волну, у которой вектор Пойнтинга
направлен вдоль оси координат в положительном направлении. При этом под
терминами прямая и обратная волны мы понимает волны с разным направлением
волнового вектора. Для количественного их описания нам удобно использовать не
постоянную распространения, а определенный выше коэффициент замедления ![]() (см. формулу (1)).
(см. формулу (1)).
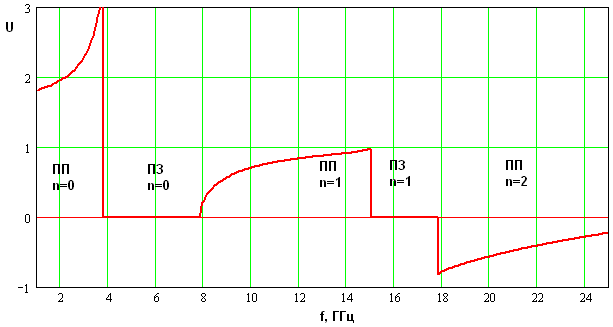
Рис. 2. Частотная зависимость коэффициента замедления основной волны ЭМК.
На рис. 2
показана типичная частотная зависимость коэффициента замедления основной волны
линейного ЭМК. Она получена для следующих параметров: ![]() ,
,
![]() ,
, ![]() ,
, ![]() . Здесь и далее все геометрические размеры
даны в миллиметрах, а емкость в пикофарадах.
. Здесь и далее все геометрические размеры
даны в миллиметрах, а емкость в пикофарадах.
Из рис. 2 видны
характерные режимы распространения основной волны ЭМК. На низких частотах волна
имеет замедленный характер, так как ![]() . Наличие полосы
пропускания на низких частотах обусловлено емкостным характером элемента,
включенного в металлический цилиндр. Его сопротивление стремится к
бесконечности при
. Наличие полосы
пропускания на низких частотах обусловлено емкостным характером элемента,
включенного в металлический цилиндр. Его сопротивление стремится к
бесконечности при ![]() и поэтому токи, текущие по
цилиндрам стремятся к нулю. Это эквивалентно отсутствию цилиндров в структуре,
что делает возможным распространение волны в ЭМК на низких частотах. Указанной
наиболее низкочастотной полосе пропускания присвоим нулевой номер.
и поэтому токи, текущие по
цилиндрам стремятся к нулю. Это эквивалентно отсутствию цилиндров в структуре,
что делает возможным распространение волны в ЭМК на низких частотах. Указанной
наиболее низкочастотной полосе пропускания присвоим нулевой номер.
Начиная с некоторой частоты, которая в рассматриваемом случае близка к 4 ГГц, волна становится нераспространяющейся, что соответствует режиму запрещенной зоны или полосы запирания. В этом режиме коэффициент замедления равен нулю, так как равна нулю действительная часть постоянной распространения. Возникновение запрещенной зоны, которой присвоим нулевой номер, связано с уменьшением емкостного сопротивления и увеличением влияния цилиндров на параметры волны в ЭМК.
Следующая после
нулевой полосы запирания первая полоса пропускания характеризуется тем, что в
ней волна имеет быстрый характер ![]() . Она распространяется
вплоть до частот, на которых периоды решетки ЭМК становятся сравнимыми с
половиной длины волны в свободном пространстве. На этих частотах возникает
первая полоса запирания, которую часто также называют Брэгговской запрещенной
зоной.
. Она распространяется
вплоть до частот, на которых периоды решетки ЭМК становятся сравнимыми с
половиной длины волны в свободном пространстве. На этих частотах возникает
первая полоса запирания, которую часто также называют Брэгговской запрещенной
зоной.
После первой полосы запирания следует вторая полоса пропускания, в которой распространяется обратная волна, имеющая отрицательный коэффициент замедления (см. рис. 2). Интересно, что, несмотря на смену знака у коэффициента замедления, он всегда растет с ростом частоты. Таким образом, даже обратная волна имеет нормальную частотную дисперсию коэффициента замедления.
На рис. 3 показана
частотная зависимость модуля коэффициента замедления основной волны ЭМК. Кривые
1 – 3 получены для разных значений емкости ![]() 0.1,
0.2, 0.5. Видно, что во второй полосе пропускания коэффициент замедления весьма
слабо зависит от емкости. В первой полосе пропускания от нее в основном
меняется только нижняя граничная частота.
0.1,
0.2, 0.5. Видно, что во второй полосе пропускания коэффициент замедления весьма
слабо зависит от емкости. В первой полосе пропускания от нее в основном
меняется только нижняя граничная частота.
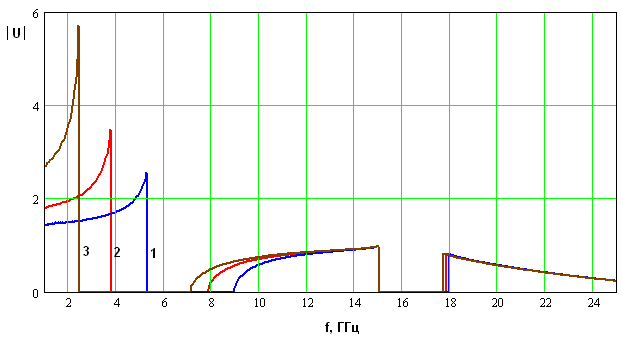
Рис. 3. Частотная зависимость модуля коэффициента замедления основной волны ЭМК.
Из рис. 2 и 3 видно, что поиск условий синхронизма имеет смысл проводить в первой и второй полосах пропускания, в которых распространяются прямые и обратные волны. Нам необходимо убедиться, что они могут иметь одинаковые по модулю коэффициенты замедления на частотах отличающихся в два раза.
Для решения
поставленной задачи проще всего построить два графика. Первый из них – это частотная
зависимость модуля коэффициента замедления от частоты ![]() ,
а второй – частотная зависимость модуля коэффициента замедления от
,
а второй – частотная зависимость модуля коэффициента замедления от ![]() . Точка пересечения этих графиков дает нам
частоту, на которой выполняется условие пространственного синхронизма
противонаправленных волн ЭМК.
. Точка пересечения этих графиков дает нам
частоту, на которой выполняется условие пространственного синхронизма
противонаправленных волн ЭМК.
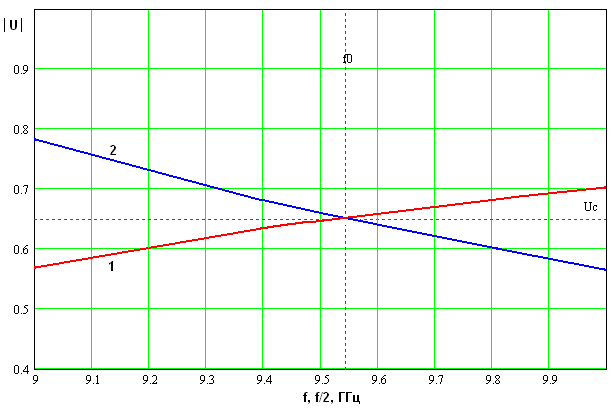
На рис. 4 показаны
обсуждавшиеся выше графики. Кривая 1 соответствует функции ![]() , а кривая 2 функции
, а кривая 2 функции ![]() . Из рис. 4 видно, что кривые 1 и 2
действительно пересекаются на частоте
. Из рис. 4 видно, что кривые 1 и 2
действительно пересекаются на частоте ![]() . В
точке пересечения коэффициенты замедления равны по модулю величине
. В
точке пересечения коэффициенты замедления равны по модулю величине ![]() . Для рассматриваемого примера
. Для рассматриваемого примера ![]() =0.65.
=0.65.
Рис. 4. К определению условий пространственного синхронизма.
Найденные параметры
ЭМК, при которых реализуется режим пространственного синхронизма не являются
уникальными. На рис. 5, который аналогичен рис. 4 показаны частотные
зависимости коэффициента замедления, полученные для следующих параметров ЭМК: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Из
рис. 5 видно, что при этих параметрах синхронизм возникает на частоте 5.18 ГГц.
. Из
рис. 5 видно, что при этих параметрах синхронизм возникает на частоте 5.18 ГГц.
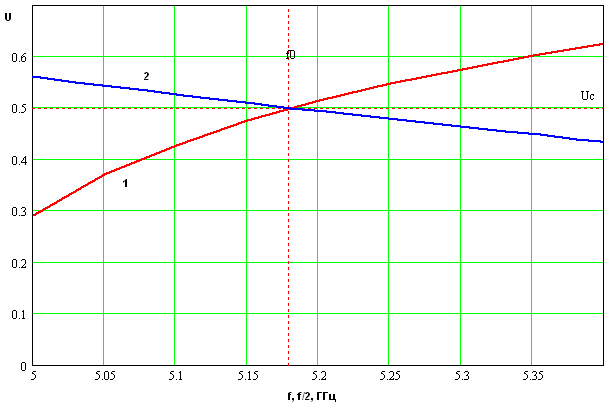
Рис. 5. Частотные зависимости коэффициента замедления волн на кратных частотах.
4. Генерация второй гармоники
Рассмотрим далее
результаты численного решения системы нелинейных уравнений (1). Численный
анализ полубесконечного или бесконечного по оси 0х ЭМК представляет большие сложности.
Поэтому будем исследовать структуру конечной длины, которая описывается числом
элементов ЭМК вдоль оси 0х ![]() . Для нее можно
определить внешние параметры рассеяния: коэффициенты отражения
. Для нее можно
определить внешние параметры рассеяния: коэффициенты отражения ![]() и прохождения
и прохождения ![]() .
Индекс
.
Индекс ![]() соответствует номеру гармоники частоты,
на которой происходит возбуждение ЭМК, а индекс
соответствует номеру гармоники частоты,
на которой происходит возбуждение ЭМК, а индекс ![]() гармонике,
на которой наблюдается реакция ЭМК в виде отраженной или прошедшей волны. Отметим,
что при определении параметров рассеяния под амплитудой волны на частоте
гармонике,
на которой наблюдается реакция ЭМК в виде отраженной или прошедшей волны. Отметим,
что при определении параметров рассеяния под амплитудой волны на частоте ![]() мы понимаем комплексную величину, у
которой модуль равен корню из суммарной мощности, переносимой волнами на
частотах
мы понимаем комплексную величину, у
которой модуль равен корню из суммарной мощности, переносимой волнами на
частотах ![]() и
и ![]() , а
фаза равна фазе компоненты электрического поля
, а
фаза равна фазе компоненты электрического поля ![]() . При
таком определении параметров рассеяния сумма квадратов их модулей равна единице
в силу закона сохранения энергии.
. При
таком определении параметров рассеяния сумма квадратов их модулей равна единице
в силу закона сохранения энергии.
Также необходимо
отметить, что мы предполагаем, что период ЭМК ![]() достаточно
мал и в ЭМК не возбуждаются пространственные гармоники порядка выше нулевого.
Структура, показанная на рис. 1 возбуждается плоской волной слева на основной
частоте. Основной интерес на данном этапе представляет исследование параметров
рассеяния структуры, описывающих волны удвоенной частоте.
достаточно
мал и в ЭМК не возбуждаются пространственные гармоники порядка выше нулевого.
Структура, показанная на рис. 1 возбуждается плоской волной слева на основной
частоте. Основной интерес на данном этапе представляет исследование параметров
рассеяния структуры, описывающих волны удвоенной частоте.
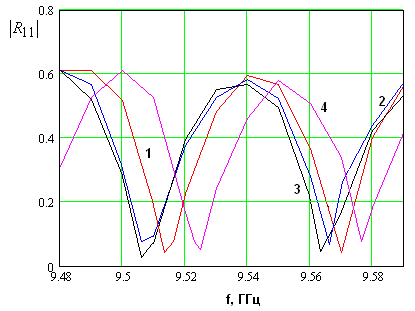
Рис. 6. Частотная
зависимость модуля коэффициента отражения ![]() .
.
На рис. 6 показана
зависимость от частоты модуля коэффициента отражения волны на первой гармонике ![]() . Кривые 1-4 соответствуют разным
значениям амплитуды падающей волны, которые равны 7, 10, 13 и 20 В. Графики на
рис. 6 получены для следующих параметров ЭМК:
. Кривые 1-4 соответствуют разным
значениям амплитуды падающей волны, которые равны 7, 10, 13 и 20 В. Графики на
рис. 6 получены для следующих параметров ЭМК: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
Зависимость емкости от напряжения взята в стандартной для СВЧ диодов форме [7]:
.
Зависимость емкости от напряжения взята в стандартной для СВЧ диодов форме [7]:
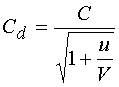 , (7)
, (7)
где ![]() -
напряжение пробоя диода взято равным –20 В.
-
напряжение пробоя диода взято равным –20 В.
Из рис. 6 видно, что
в окрестности частоты синхронизма, которая равна 9.53 ГГц (см. рис. 4)
коэффициент отражения ![]() меняется с частотой
периодически. Такое поведение типично, для структур с двумя плоскими границами.
меняется с частотой
периодически. Такое поведение типично, для структур с двумя плоскими границами.
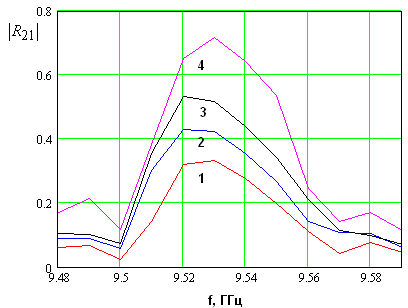
На рис. 7 показана частотная зависимость модуля коэффициента отражения волны на второй гармонике. Кривые 1-4 соответствуют тем же значениям напряжения падающей волны, что и раньше. Параметры ЭМК остались неизменными.
Рис. 7. Частотная
зависимость модуля коэффициента отражения ![]() .
.
Видно, что модуль коэффициента отражения на второй гармонике в окрестности частоты синхронизма достаточно резко растет и достигает максимума на указанной частоте. Величина максимума сильно зависит от напряжения возбуждающей волны. Таким образом, мы можем сделать вывод о том, что интенсивность генерации второй гармоники в режиме синхронизма противонаправленных волн действительно существенно растет, что является следствием усиления нелинейного взаимодействия волн ЭМК.
Представляют интерес распределения амплитуд напряжений и токов в элементах ЭМК. Графики, представленные на рис. 8 – 12, построены для падающей волны с напряжением 20 В. Видно, что амплитуды напряжений на элементах ЭМК убывают при удалении от его левой границы.
На рис. 8 показано амплитудное распределение напряжений основной частоты на нелинейных емкостях на частоте 9.53 ГГц.
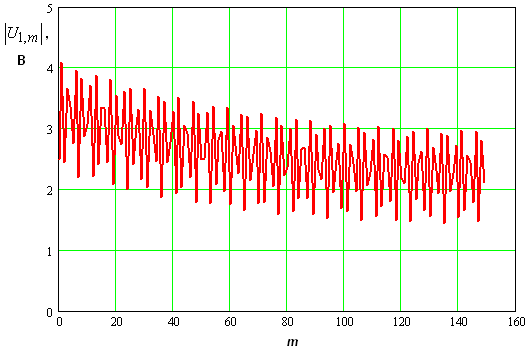
Рис. 8. Амплитудное распределение напряжений на основной частоте в условиях пространственного синхронизма.
На рис. 9 показано амплитудное распределение на той же частоте напряжений второй гармоники, а на рис. 10 это же распределение, на частоте 9.1 ГГц, то есть вне пределов полосы пространственного синхронизма.
Видно, что пространственный синхронизм меняет качественный характер амплитудного распределения, что особенно сильно проявляется на второй частотной гармонике, на которой убывающий вид решения особенно хорошо заметен.
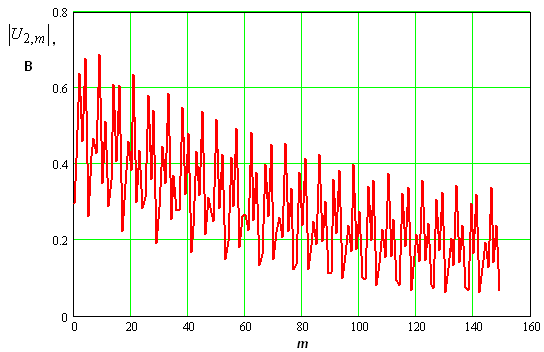
Рис. 9. Амплитудное распределение напряжений на второй гармонике в условиях пространственного синхронизма.
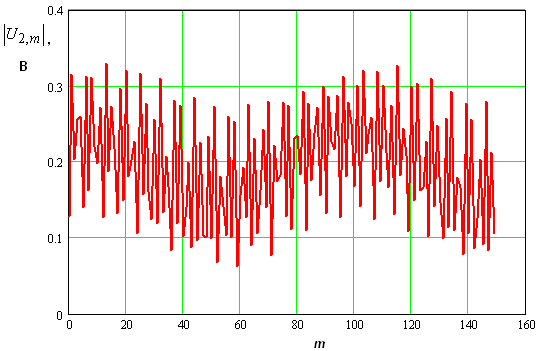
Рис. 10. Амплитудное распределение напряжений на второй гармонике вне пределов полосы пространственного синхронизма.
На рис. 11, 12 представлены амплитудные распределения первой и второй гармоник токов, текущих через нелинейные емкости. Первые гармоники токов ведут себя аналогично напряжениям на емкостях. Распределение токов на второй гармонике отличается от распределения напряжений.
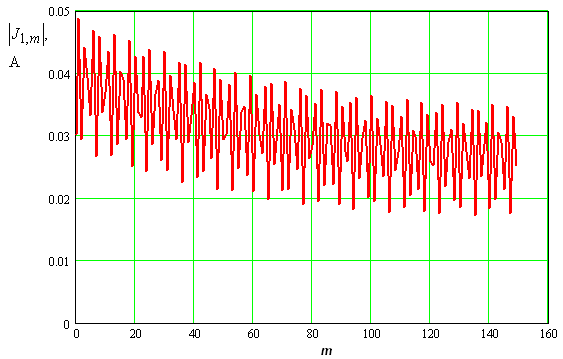
Рис. 11. Амплитудное распределение токов на основной частоте в условиях пространственного синхронизма.
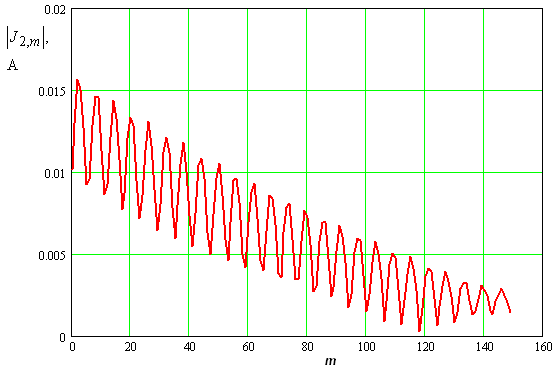
Рис. 12. Амплитудное распределение токов на второй гармонике в условиях пространственного синхронизма.
Дополнительную информацию об амплитудных распределениях токов и напряжений может дать их спектральный анализ. Для этого будем анализировать следующие функции:
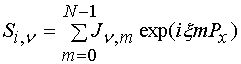 .
.
Из выражений (8)
видно, что функции ![]() - это спектр пространственных
частот
- это спектр пространственных
частот ![]() распределения напряжений на частоте
распределения напряжений на частоте ![]() . Функция
. Функция ![]() имеет
такой же смысл, но для распределения токов.
имеет
такой же смысл, но для распределения токов.
а
б
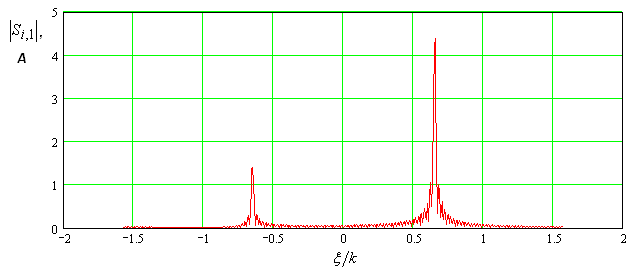
Рис. 13. Спектры пространственных частот напряжений (а) и токов (б) на основной частоте.
На рис. 13
а,б показаны модули функций ![]() и
и ![]() , а на рис. 14 а,б те же функции, но
соответствующие второй гармонике. Графики на рис. 13 и 14 построены для частоты
9.53 ГГц напряжения падающей волны 20 В.
, а на рис. 14 а,б те же функции, но
соответствующие второй гармонике. Графики на рис. 13 и 14 построены для частоты
9.53 ГГц напряжения падающей волны 20 В.
а
б
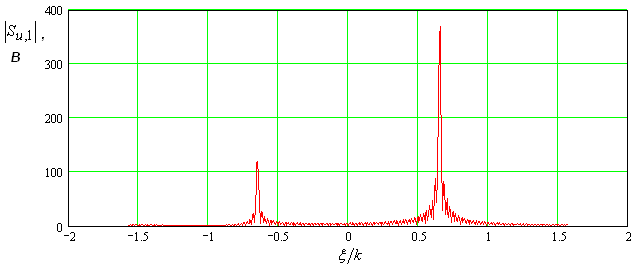
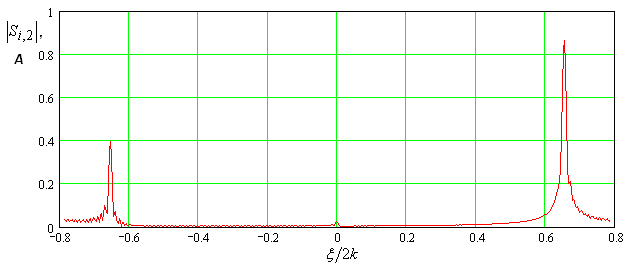
Рис. 14. Спектры пространственных частот напряжений (а) и токов (б) на второй гармонике.
Анализ спектральных
функций напряжений и токов первой гармоники показывает, что качественно они
похожи друг на друга. В них можно выделить два максимума при ![]() , то есть на пространственных частотах
нормированных на волновое число свободного пространства равных по модулю
коэффициенту замедления собственных волн ЭМК на частоте пространственного
синхронизма
, то есть на пространственных частотах
нормированных на волновое число свободного пространства равных по модулю
коэффициенту замедления собственных волн ЭМК на частоте пространственного
синхронизма ![]() . Максимумы имеют разные амплитуды, что
говорит о том, что прямая и обратная волны возбуждаются с разными амплитудами.
. Максимумы имеют разные амплитуды, что
говорит о том, что прямая и обратная волны возбуждаются с разными амплитудами.
Спектральный анализ
распределений амплитуд и токов второй гармоники показывает, что распределения
напряжений и токов имеют качественные отличия. Эти распределения показаны
на рис. 14 а,б. По оси абсцисс отложен параметр ![]() .
Видно, что наряду с максимумами на пространственных частотах
.
Видно, что наряду с максимумами на пространственных частотах ![]() спектр распределения напряжений имеет
максимум в окрестности нулевой пространственной частоты.
спектр распределения напряжений имеет
максимум в окрестности нулевой пространственной частоты.
Кривые на рис. 13, 14
а,б показывают, что в спектрах пространственных частот на обеих гармониках
доминируют волны в фазовом смысле распространяющиеся вперед. Они имеют
одинаковое направление волновых векторов. Однако, на частоте ![]() волна является прямой. Поэтому ее вектор
Пойнтинга также направлен вдоль оси 0х. На частоте
волна является прямой. Поэтому ее вектор
Пойнтинга также направлен вдоль оси 0х. На частоте ![]() волна
в ЭМК является обратной. Таким образом, ее вектор Пойнтинга ориентирован в
отрицательном направлении оси 0х. Поэтому в энергетическом смысле волна на
частотах
волна
в ЭМК является обратной. Таким образом, ее вектор Пойнтинга ориентирован в
отрицательном направлении оси 0х. Поэтому в энергетическом смысле волна на
частотах ![]() и
и ![]() распространяются
в разных направлениях (см. рис. 15).
распространяются
в разных направлениях (см. рис. 15).
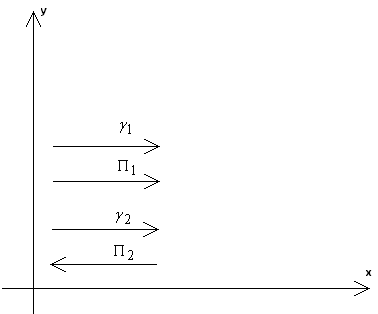
Рис. 15. Ориентация волновых векторов и векторов Пойнтинга.
Распространение волны на второй гармоники в отрицательном направлении объясняет рост коэффициента отражения в окрестности частоты пространственного синхронизма (см. рис. 7).
Наличие в спектрах
(см. рис. 13,14 а,б) компонент на отрицательных пространственных частотах,
которые соответствуют встречным волнам можно объяснить отражением от границ
ЭМК. Появление волн с волновыми векторами, ориентированными вдоль оси 0х в
отрицательном направлении объясняет появление существенных компонент на частоте
![]() с нулевой пространственной частотой.
Напряжение на этой частоте пропорционально в первом приближении квадрату
напряжения на частоте
с нулевой пространственной частотой.
Напряжение на этой частоте пропорционально в первом приближении квадрату
напряжения на частоте ![]() . Если оно описывается суммой
прямой и встречной волн, то такая сумма, возведенная в квадрат, даст
составляющую с нулевой пространственной частотой.
. Если оно описывается суммой
прямой и встречной волн, то такая сумма, возведенная в квадрат, даст
составляющую с нулевой пространственной частотой.
5. Параметрическое усиление на основной частоте
Следующий
эффект, который будет представлен в работе – это эффект параметрического
усиления сигнала на основной частоте при его взаимодействии с сигналом на
удвоенной частоте ![]() . Сигнал на второй гармонике
принято называть сигналом накачки. При этом имеется в виду, что его мощность
много больше мощности волны на основной частоте.
. Сигнал на второй гармонике
принято называть сигналом накачки. При этом имеется в виду, что его мощность
много больше мощности волны на основной частоте.
Мы
рассмотрим два варианта реализации параметрического усиления. Они отличаются
направлением распространения волны накачки на удвоенной частоте. Пусть сигнал
основной частоты поступает на ЭМК слева. Тогда в одном режиме волна накачки
набегает на ЭМК справа, а в другом слева. На первый взгляд, если исходить из
диаграммы, показанной на рис. 15 эффект усиления должен иметь место только при
возбуждении ЭМК на частоте ![]() слева. Однако, как
показали численные расчеты, он возникает в обоих случаях. О причинах усиления
при возбуждении ЭМК на двух частотах с одной стороны мы будем говорить ниже.
слева. Однако, как
показали численные расчеты, он возникает в обоих случаях. О причинах усиления
при возбуждении ЭМК на двух частотах с одной стороны мы будем говорить ниже.
Для
количественной характеристики исследуемого процесса целесообразно ввести
коэффициент усиления сигнала основной частоты. Пусть ![]() -
мощность волны основной частоты, падающей на ЭМК, которая приходится на один
период ЭМК по оси 0у. Эта мощность легко определяется через амплитуду падающей
волны (4):
-
мощность волны основной частоты, падающей на ЭМК, которая приходится на один
период ЭМК по оси 0у. Эта мощность легко определяется через амплитуду падающей
волны (4):
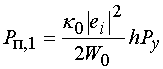 , (9)
, (9)
где ![]() -
волновое сопротивление свободного пространства.
-
волновое сопротивление свободного пространства.
Нас интересует
мощность первой гармоники частоты, рассеянная ЭМК. Она складывается из мощности
волн отраженных от и прошедших через ЭМК. Их можно определить, используя
параметры рассеяния ![]() и
и ![]() .
Индексы 1,1 показывают, что параметры рассеяния определяются через отношение
амплитуд волн на частоте
.
Индексы 1,1 показывают, что параметры рассеяния определяются через отношение
амплитуд волн на частоте ![]() . При этом амплитуда
волны, падающей на ЭМК на частоте
. При этом амплитуда
волны, падающей на ЭМК на частоте ![]() не равна нулю.
не равна нулю.
Нетрудно показать,
что отношение мощностей волн рассеянных ЭМК на основной частоте к мощности
падающей волны ![]() определяется параметрами
рассеяния:
определяется параметрами
рассеяния:
![]() , (10)
, (10)
где ![]() -
коэффициент усиления по мощности. Строго говоря, параметр
-
коэффициент усиления по мощности. Строго говоря, параметр ![]() имеет смысл называть коэффициентом
усиления только, когда он превышает единицу. Однако для простоты мы будем
использовать этот термин также при
имеет смысл называть коэффициентом
усиления только, когда он превышает единицу. Однако для простоты мы будем
использовать этот термин также при ![]() .
.
Для полного описания
взаимодействия волн в нелинейном ЭМК полезно ввести коэффициент преобразования ![]() мощности волны накачки в мощность волны
на основной частоте:
мощности волны накачки в мощность волны
на основной частоте:
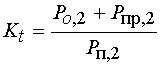 , (11)
, (11)
где ![]() -
мощность падающей волны на второй гармонике, а
-
мощность падающей волны на второй гармонике, а ![]() и
и ![]() - мощности отраженной и прошедшей волн на
той же частоте. Нетрудно показать, что коэффициент
- мощности отраженной и прошедшей волн на
той же частоте. Нетрудно показать, что коэффициент ![]() выражается
через параметры рассеяния:
выражается
через параметры рассеяния:
Известно [2], что при
двухчастотном взаимодействии волн важное значение имеет разность фаз между их
амплитудами. Для описания этой разности фаз введем следующий параметр ![]() :
:
![]() , (13)
, (13)
где ![]() -
фазы амплитуд волн, падающих на ЭМК в сечении
-
фазы амплитуд волн, падающих на ЭМК в сечении ![]() . Фазы
определяются для компоненты электрического поля
. Фазы
определяются для компоненты электрического поля ![]() .
.
Для характеристики
интенсивности падающих волн на частоте ![]() и
и ![]() удобно ввести также ее напряжения
удобно ввести также ее напряжения ![]() , которые являются произведениями
напряженности электрического поля (см. формулу (4)) на высоту ПВ
, которые являются произведениями
напряженности электрического поля (см. формулу (4)) на высоту ПВ ![]() .
.
Параметрическое усиление
при возбуждении ЭМК с разных сторон. В ходе численных экспериментов
исследовались, в первую очередь, зависимости параметра ![]() от
частоты, разности фаз
от
частоты, разности фаз ![]() и напряжения
и напряжения ![]() .
.
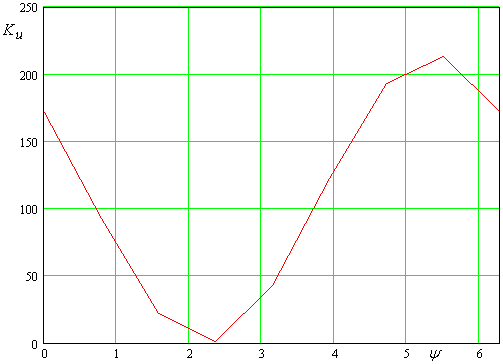
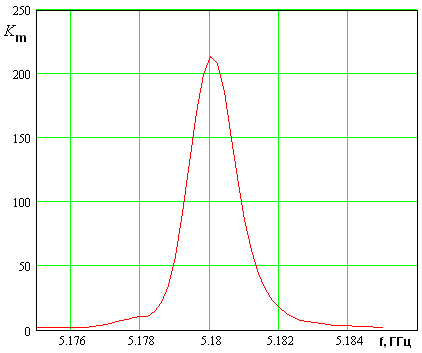
Типичная зависимость
коэффициента усиления от разности фаз ![]() показана
на рис. 16. Кривая на рис. 16 получена при
показана
на рис. 16. Кривая на рис. 16 получена при ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() ГГц,
ГГц, ![]() В,
В, ![]() В.
Аналогичные кривые были получены для дискретного набора частот, изменяющихся в
диапазоне от 5.175 ГГц до 5.185 ГГц и значений параметра
В.
Аналогичные кривые были получены для дискретного набора частот, изменяющихся в
диапазоне от 5.175 ГГц до 5.185 ГГц и значений параметра ![]() , изменяющегося от нуля до
, изменяющегося от нуля до ![]() с шагом
с шагом ![]() .
.
Рис. 16.
Зависимость коэффициента
усиления от разности фаз ![]() .
.
Из рис. 16 видно, что зависимость коэффициента усиления от разности фаз волн хорошо описывается следующей функцией:
где ![]() -
максимальное значение коэффициента усиления, которое достигается при
-
максимальное значение коэффициента усиления, которое достигается при ![]() . Из формулы (14) следует, что минимум
параметра
. Из формулы (14) следует, что минимум
параметра ![]() наблюдается при
наблюдается при ![]() ,
,
![]() .
.
Параметры ![]() ,
, ![]() и
и ![]() являются функциями частоты. Для них были
построены сплайн аппроксимации, позволяющие находит их значения для
произвольной частоты в пределах указанного выше диапазона.
являются функциями частоты. Для них были
построены сплайн аппроксимации, позволяющие находит их значения для
произвольной частоты в пределах указанного выше диапазона.
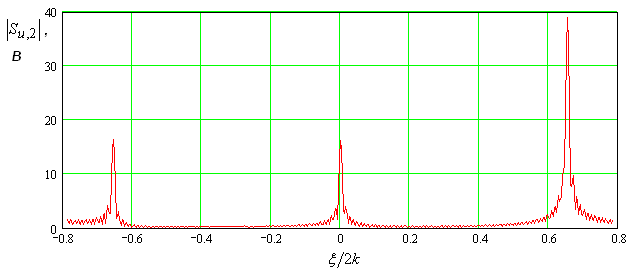
На рис. 17 показана
частотная зависимость максимального коэффициента усиления ![]() . Видно, что она напоминает резонансную
кривую, которая достигает максимума в окрестности частоты пространственного
синхронизма волн ЭМК 5.18 ГГц. Анализируя частотную зависимость параметра
. Видно, что она напоминает резонансную
кривую, которая достигает максимума в окрестности частоты пространственного
синхронизма волн ЭМК 5.18 ГГц. Анализируя частотную зависимость параметра ![]() можно определить добротность ЭМК
можно определить добротность ЭМК ![]() как отношение резонансной частоты 5.18
ГГц к ширине кривой по уровню половины от максимального значения. Получаем, что
как отношение резонансной частоты 5.18
ГГц к ширине кривой по уровню половины от максимального значения. Получаем, что
![]() =3237.
=3237.
Рис. 17. Зависимость максимального значения коэффициента усиления от частоты.
Таким образом, мы можем сделать вывод о том, что интенсивное усиление сигнала основной частоты имеет характер высокодобротного резонанса и наблюдается в узкой полосе частот.
На рис. 18 показана
частотная зависимость параметров ![]() и
и ![]() . Кривая 1 соответствует
. Кривая 1 соответствует ![]() , а кривая 2
, а кривая 2 ![]() . Из рис.
18 видно, что разность фаз, при которой коэффициент усиления достигает
максимума зависит от частоты практически линейно.
. Из рис.
18 видно, что разность фаз, при которой коэффициент усиления достигает
максимума зависит от частоты практически линейно.
Представляет интерес
распределение амплитуд напряжений первой и второй гармоник на нелинейных
элементах ![]() . Такое распределение показано на рис. 19.
Кривые на рис. 19. получены при
. Такое распределение показано на рис. 19.
Кривые на рис. 19. получены при ![]() В,
В, ![]() ,
, ![]() ГГц.
Остальные параметры остались без изменений. Видно, что распределение модулей
амплитуд напряжений на основной частоте (кривая 1) имеет осциллирующий характер
с глубокими провалами. В среднем напряжения растут при удалении от точки
возбуждения (m=0) волны на частоте
ГГц.
Остальные параметры остались без изменений. Видно, что распределение модулей
амплитуд напряжений на основной частоте (кривая 1) имеет осциллирующий характер
с глубокими провалами. В среднем напряжения растут при удалении от точки
возбуждения (m=0) волны на частоте ![]() . Распределение амплитуд напряжений на
удвоенной частоте слабо осциллирует и мало зависит от номера
. Распределение амплитуд напряжений на
удвоенной частоте слабо осциллирует и мало зависит от номера ![]() .
.
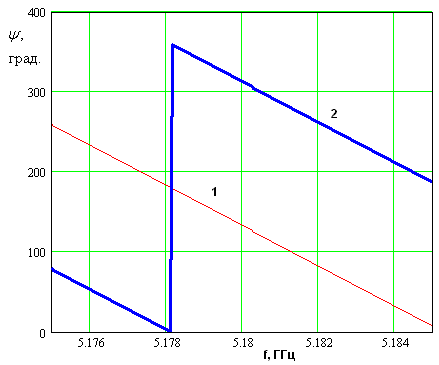
Рис. 18.
Частотная зависимость параметров ![]() и
и ![]() .
.
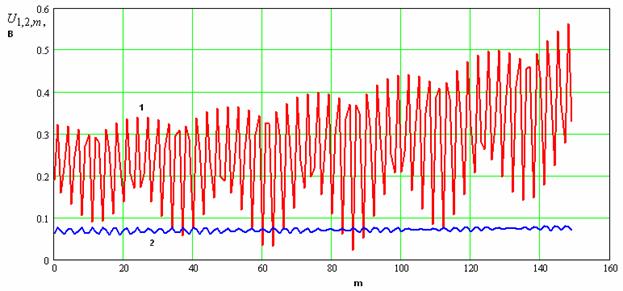
Рис. 19. Распределение модулей амплитуд напряжений на нелинейных элементах.
Большое значение
коэффициента усиления в несколько сотен нельзя объяснить ростом напряжения
первой гармоники с увеличением номера ![]() , так
как напряжения при
, так
как напряжения при ![]() и
и ![]() отличаются
всего в несколько раз. Усиление связано с общим ростом напряжения во всех
элементах ЭМК. Такое поведение напряжения лишний раз говорит о том, что мы
имеем дело с некоторым резонансом внутри ЭМК, который отличается от
взаимодействия двух прямых волн в нелинейной среде [2].
отличаются
всего в несколько раз. Усиление связано с общим ростом напряжения во всех
элементах ЭМК. Такое поведение напряжения лишний раз говорит о том, что мы
имеем дело с некоторым резонансом внутри ЭМК, который отличается от
взаимодействия двух прямых волн в нелинейной среде [2].
Дополнительную информацию о характере параметрического усиления можно получить, анализируя спектр пространственных частот. Определение этого спектра было дано в разделе 4 (см. формулу (8)).
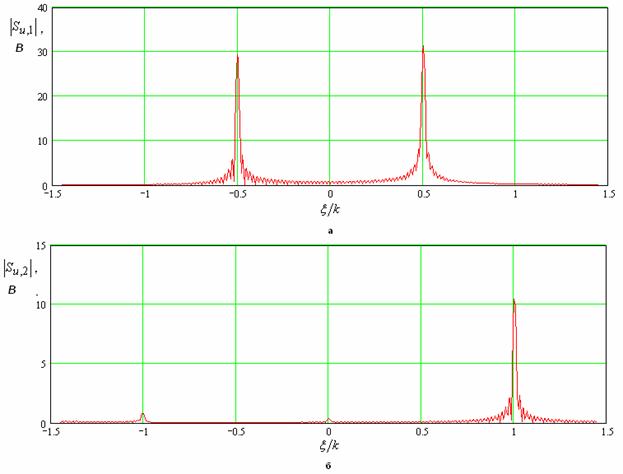
Рис. 20. Спектры пространственных частот первой и второй гармоник напряжения.
На рис. 20 а,б показаны спектры пространственных частот, полученные для распределений амплитуд представленных на рис. 19. Обращают на себя внимание практически одинаковые амплитуды прямой и встречной волн на основной частоте. На второй гармонике спектр имеет выраженный несимметричный характер. Преобладает волна, которая в энергетическом смысле распространяется в отрицательном направлении. Видны также существенно меньшие по амплитуде пики, соответствующие волне, распространяющейся в прямом направлении и волне с нулевой пространственной частотой.
На рис. 21 показана зависимость максимального значения коэффициента усиления, выраженного в децибелах от напряжения волны накачки. Данная зависимость позволяет выделить несколько режимов работы ЭМК.
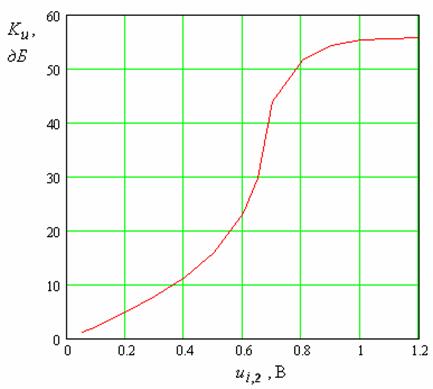
Рис. 21. Зависимость коэффициента усиления от напряжения возбуждающей волны первой гармоники.
При сравнительно
малой интенсивности накачки коэффициент усиления растет экспоненциально. Об
этом свидетельствует линейный участок кривой зависимости ![]() . Этот участок заканчивается при
. Этот участок заканчивается при ![]() В. При больших напряжениях наблюдается
участок резкого роста коэффициента усиления. Мы наблюдаем некоторый пороговый
эффект, который сопровождает переход от режима экспоненциального роста к режиму
насыщения, в котором рост коэффициента усиления практически прекращается (см.
правый участок кривой на рис. 21).
В. При больших напряжениях наблюдается
участок резкого роста коэффициента усиления. Мы наблюдаем некоторый пороговый
эффект, который сопровождает переход от режима экспоненциального роста к режиму
насыщения, в котором рост коэффициента усиления практически прекращается (см.
правый участок кривой на рис. 21).
Интересно проследить
изменение коэффициента преобразования ![]() при
росте напряжения
при
росте напряжения ![]() . Соответствующая зависимость
показана на рис. 22. Нетрудно увидеть, что на участке экспоненциального роста
коэффициент преобразования в децибелах практически равен нулю. Это означает,
что волна накачки передает малую долю своей мощности волне основной частоты.
При этом, тем не менее, коэффициент усиления может достигать весьма больших
значений, поскольку напряжение волны на основной частоте много меньше
напряжения волны накачки (0.001<<0.6).
. Соответствующая зависимость
показана на рис. 22. Нетрудно увидеть, что на участке экспоненциального роста
коэффициент преобразования в децибелах практически равен нулю. Это означает,
что волна накачки передает малую долю своей мощности волне основной частоты.
При этом, тем не менее, коэффициент усиления может достигать весьма больших
значений, поскольку напряжение волны на основной частоте много меньше
напряжения волны накачки (0.001<<0.6).
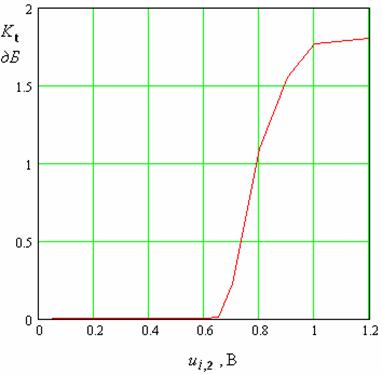
Рис. 22. Зависимость коэффициента преобразования от напряжения волны накачки.
В переходном режиме
мы видим резкое усиление взаимодействия волн разных частот, которое приводит к
увеличению коэффициента преобразования. При дальнейшем увеличении напряжения
волны накачки происходит стабилизация параметра ![]() при
значении близком к 2 дБ. Такое значение коэффициента преобразования говорит о
том, что в волну основной частоты может быть передано не более одной трети
мощности волны накачки.
при
значении близком к 2 дБ. Такое значение коэффициента преобразования говорит о
том, что в волну основной частоты может быть передано не более одной трети
мощности волны накачки.
Параметрическое усиление при возбуждении ЭМК с одной стороны. Рассмотрим далее возбуждение ЭМК волнами на основной и удвоенной частотах с одной стороны. Отметим сразу, что изменение направления распространения волны накачки не привело к качественным изменениям характеристик параметрического усиления. Поэтому будем описывать его с помощью параметров введенных выше. Также оставим без изменения геометрические размеры ЭМК.
На рис. 23
представлены кривые зависимости коэффициента усиления от разности фаз ![]() . Они похожи на кривую, изображенную на
рис. 16. Кривые 1 – 4 получены при
. Они похожи на кривую, изображенную на
рис. 16. Кривые 1 – 4 получены при ![]() В,
В, ![]() В. Они соответствуют частотам 5.177,
5.178, 5.179, 5.18 ГГц. Видно, что для описания кривых подходит аппроксимация
(14). Используя ее, можно построить зависимости параметров
В. Они соответствуют частотам 5.177,
5.178, 5.179, 5.18 ГГц. Видно, что для описания кривых подходит аппроксимация
(14). Используя ее, можно построить зависимости параметров ![]() ,
, ![]() и
и ![]() от частоты.
от частоты.
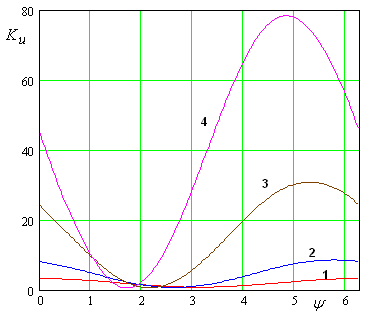
Рис. 23.
Зависимость коэффициента усиления от разности фаз ![]() .
.
На рис. 24 показана частотная зависимость максимального коэффициента усиления. Она близка к резонансной кривой. Эквивалентная добротность равна 2726. Сравнивая кривые на рис. 24 и 17, можно отметить, что при одностороннем возбуждении ЭМК абсолютное значение коэффициента усиления уменьшается.
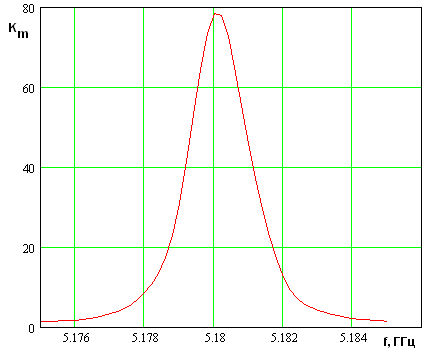
Рис. 24. Частотная зависимость максимального коэффициента усиления.
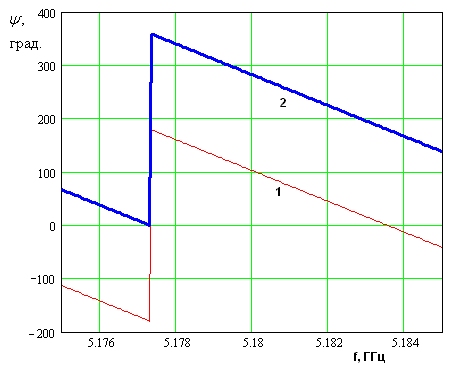
Рис. 25. Частотная
зависимость параметров ![]() и
и ![]() .
.
Параметры ![]() и
и ![]() линейно
зависят частоты (см. рис. 25). Кривая 1 соответствует
линейно
зависят частоты (см. рис. 25). Кривая 1 соответствует ![]() ,
а кривая 2
,
а кривая 2 ![]() .
.
Амплитудное распределение напряжений на нелинейных элементах показано на рис. 26. Кривая 1 соответствует первой гармонике, а 2 второй.
Отличие распределения
на рис. 26 от распределения на рис. 19 состоит в том, что теперь на основной
частоте оно носит спадающий в среднем характер, тогда как ранее оно в среднем
возрастало при удалении от сечения ![]() .
.
В заключение на рис. 27 а,б приводятся зависимости коэффициентов усиления и преобразования от напряжения волны накачки. Они ведут себя полностью аналогично кривым, показанным на рис. 21 и 22.
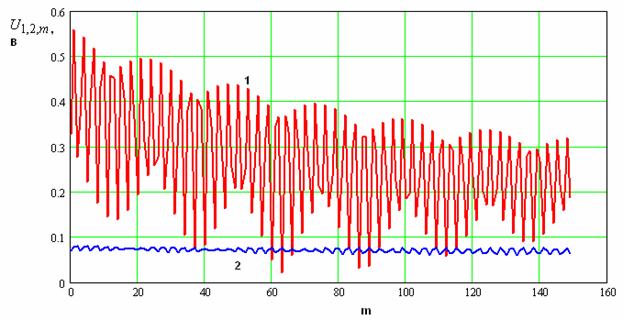
Рис. 26. Распределение модулей амплитуд напряжений на нелинейных элементах.
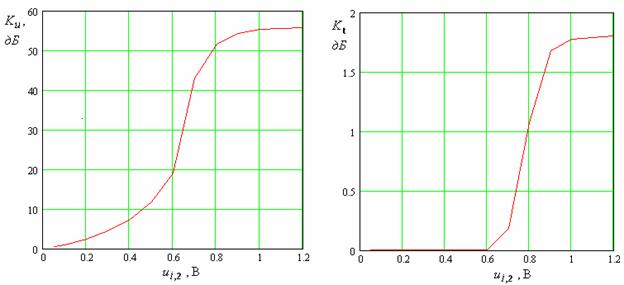
а б
Рис. 27. Зависимости коэффициентов усиления и трансформации от напряжения волны накачки.
6. Модель ЭМК в режиме пространственного синхронизма прямой и обратной волн
Непосредственное использование модели
ЭМК в виде уравнений (2) – (3) для анализа ЭМК в режиме синхронизма оказывается
неэффективным. Проблема состоит в том, что взаимодействие волн ЭМК происходит в
виде периодического или квазипериодического процесса, который формируется на
расстояниях многократно превышающих период ЭМК. Таким образом, для его
исследования необходимо анализировать электромагнитное поле в структуре с
весьма большим числом элементов вдоль оси 0х ![]() .
Прямое численное решение нелинейной системы (2) в этом случае часто
сопровождается неустойчивостью и может вообще быть расходящимся. Поэтому
возникает необходимость адаптации модели к условиям синхронизма.
.
Прямое численное решение нелинейной системы (2) в этом случае часто
сопровождается неустойчивостью и может вообще быть расходящимся. Поэтому
возникает необходимость адаптации модели к условиям синхронизма.
Уравнения (2) – (3) могут использоваться для нелинейных элементов с разной зависимостью емкости от напряжения на ней. Также в них отсутствуют ограничения на количество учитываемых гармоник. Модель, которая будет построена в данном разделе имеет ограниченную область использования. Она учитывает только взаимодействие первой и второй частотных гармоник. Кроме того, она справедлива для емкостей с простейшей линейной зависимостью от напряжения:
![]() , (15)
, (15)
которая, вообще говоря, верна
только при достаточно малых напряжениях на емкости. Емкость ![]() дает линейную часть проводимости
нелинейного элемента, а параметр
дает линейную часть проводимости
нелинейного элемента, а параметр ![]() определяет ее
нелинейную часть.
определяет ее
нелинейную часть.
При построении модели
будем использовать уже отмеченное свойство процессов в ЭМК, а именно медленное
изменение напряжений на емкостях на периоде ЭМК ![]() . Кроме
того, будем рассматривать ЭМК находящиеся в одноволновом режиме на частотах
. Кроме
того, будем рассматривать ЭМК находящиеся в одноволновом режиме на частотах ![]() и
и ![]() .
.
Сформулированные выше приближения позволяют перейти от исходной системы уравнений (2) к более простой системе:
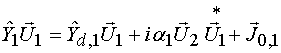 , (16)
, (16)
![]() ,
,
где ![]() ,
,
![]() - диагональные матрицы, у которых на
главной диагонали стоят линейные части проводимостей элементов ЭМК. Символ * означает операцию комплексного сопряжения.
- диагональные матрицы, у которых на
главной диагонали стоят линейные части проводимостей элементов ЭМК. Символ * означает операцию комплексного сопряжения.
Операции
над векторами в формулах (16) применяются почленно к элементам векторов с
одинаковыми индексами. Таким образом, например, ![]() - это
вектор со следующими элементами:
- это
вектор со следующими элементами:
![]() . (17)
. (17)
В развернутой форме система уравнений (16) имеет следующий вид:
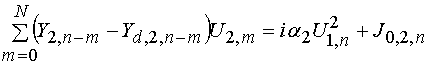 ,
, ![]() .
.
В качестве первого
шага преобразований системы (18) рассмотрим оператор, стоящий в левой части.
Считаем, что индекс ![]() меняется от минус до плюс
бесконечности. Это возможно сделать при выполнении условия:
меняется от минус до плюс
бесконечности. Это возможно сделать при выполнении условия:
![]() , при
, при ![]() ,
, ![]() .
.
Нетрудно показать, что справедливо следующее равенство:
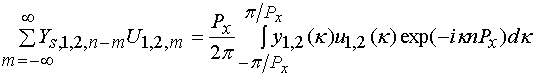 , (19)
, (19)
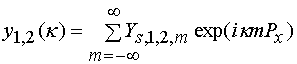 ,
,
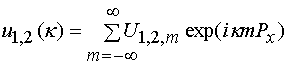 ,
,
![]() .
.
Из соотношений (19)
видно, что функция ![]() является дискретным
преобразованием Фурье последовательности
является дискретным
преобразованием Фурье последовательности ![]() .
Аналогичные утверждения справедливы для
.
Аналогичные утверждения справедливы для ![]() , а
также для
, а
также для ![]() и
и ![]() .
.
Конкретизируем далее
отмеченное выше свойство медленного изменения параметров волн в ЭМК в режиме
пространственного синхронизма. Оно состоит в том, что ![]() можно
представить в следующем виде:
можно
представить в следующем виде:
![]() , (20)
, (20)
где ![]() -
постоянные распространения собственных волн линейного ЭМК на частотах
соответственно
-
постоянные распространения собственных волн линейного ЭМК на частотах
соответственно ![]() и
и ![]() .
Непосредственно на частоте пространственного синхронизма они связаны
соотношением
.
Непосредственно на частоте пространственного синхронизма они связаны
соотношением ![]() . Экспоненциальный множитель в формуле
(20) описывает быстрые изменения напряжений на элементах ЭМК, а множитель
. Экспоненциальный множитель в формуле
(20) описывает быстрые изменения напряжений на элементах ЭМК, а множитель ![]() медленные изменения, представляющие
наибольший интерес. Из вида соотношения (20) следует, что дискретное
преобразование Фурье таких последовательностей сосредоточено в небольшой
окрестности точки
медленные изменения, представляющие
наибольший интерес. Из вида соотношения (20) следует, что дискретное
преобразование Фурье таких последовательностей сосредоточено в небольшой
окрестности точки ![]() . Поэтому в соотношении (19) мы
можем вместо точного выражения для функций
. Поэтому в соотношении (19) мы
можем вместо точного выражения для функций ![]() использовать
их приближенные представления, справедливые только в окрестности указанной выше
точки:
использовать
их приближенные представления, справедливые только в окрестности указанной выше
точки:
![]() , (21)
, (21)
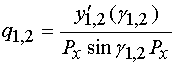 ,
,
где ![]() -
производные от соответствующих функций.
-
производные от соответствующих функций.
Подставляя соотношения (14) в выражения (12), получаем:
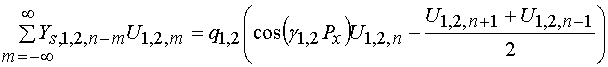 . (22)
. (22)
Из условия медленного
изменения амплитуд ![]() можно записать следующие
приближенные равенства:
можно записать следующие
приближенные равенства:
![]() , (23)
, (23)
![]() ,
,
![]() .
.
С учетом формул (23) получаем окончательное выражение для исследуемого оператора:
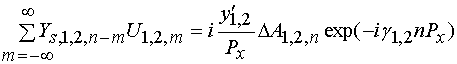 . (24)
. (24)
Строго говоря, соотношение (24) справедливо при бесконечных пределах суммирования.
Далее рассмотрим преобразование свободных членов уравнений (18). Здесь нужно отметить, что эти члены учитывают конечные размеры ЭМК, поскольку они описывают его возбуждение возможное только при условии ограниченных размеров структуры. Поэтому, если мы возьмем их в форме (5), то таким образом, учтем локальные эффекты на краях ЭМК, от которых мы хотели избавиться. Чтобы избежать этого, нам необходимо видоизменить анализируемую структуру таким образом, чтобы избежать возмущения падающих на ЭМК волн. В структуре, показанной на рис. 1, ЭМК возбуждается волнами ПВ. На границе ЭМК они испытывают сильное возмущение, обусловленное появлением цилиндров с нелинейными элементами.
Предположим, что в
новой структуре справа и слева от ЭМК также находятся периодические структуры,
состоящие из цилиндров с сосредоточенными емкостями. Однако, их емкости
являются линейными. Их проводимости не содержат нелинейной части
пропорциональной параметру ![]() . Поскольку параметр
. Поскольку параметр ![]() считается малым по сравнению с емкостью
считается малым по сравнению с емкостью ![]() параметром, то в новой структуре падающая
волна, которая будет волной линейного ЭМК, на границе нелинейного ЭМК
испытывает слабое возмущение, обусловленное только отличием нелинейной емкости
от линейной. В этом случае такими эффектами, как отражением волн от границы,
возбуждением высших типов волн и т.д. можно пренебречь и считать, что
напряжение волны внутри нелинейного ЭМК совпадает на границе с напряжением
падающей волны. Точно также при падении волны нелинейного ЭМК на его границу
она непрерывно переходит в волну линейного ЭМК.
параметром, то в новой структуре падающая
волна, которая будет волной линейного ЭМК, на границе нелинейного ЭМК
испытывает слабое возмущение, обусловленное только отличием нелинейной емкости
от линейной. В этом случае такими эффектами, как отражением волн от границы,
возбуждением высших типов волн и т.д. можно пренебречь и считать, что
напряжение волны внутри нелинейного ЭМК совпадает на границе с напряжением
падающей волны. Точно также при падении волны нелинейного ЭМК на его границу
она непрерывно переходит в волну линейного ЭМК.
С учетом сделанных выше предположений мы можем использовать для описания распространения волн внутри ЭМК однородную систему уравнений (18), а возбуждение волн на границах ЭМК описывать концевыми условиями непрерывности напряжений. Таким образом, мы приходим к следующей системе разностных уравнений:
![]() , (25)
, (25)
![]() ,
,
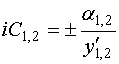 ,
,
![]() .
.
Непосредственно на
частоте пространственного синхронизма выполняется соотношение ![]() , следующее из выражения (1). Верхний знак
в формулах (25) соответствует первой гармонике, а нижний второй. Разные знаки
введены специально, чтобы коэффициенты
, следующее из выражения (1). Верхний знак
в формулах (25) соответствует первой гармонике, а нижний второй. Разные знаки
введены специально, чтобы коэффициенты ![]() были
положительными действительными числами. Коэффициент
были
положительными действительными числами. Коэффициент ![]() оказывается
при таком определении положительной величиной благодаря тому, что производная
оказывается
при таком определении положительной величиной благодаря тому, что производная ![]() для обратной волны имеет отрицательный
знак.
для обратной волны имеет отрицательный
знак.
Непосредственно в режиме синхронизма система (25) имеет следующий вид:
![]() , (26)
, (26)
![]() .
.
Для аналитического
исследования решения граничной задачи разностные уравнения (26) можно
приближенно преобразовать к дифференциальным уравнениям. Такое преобразование
справедливо, вообще говоря, в пределе при ![]() .
Однако, принимая во внимание медленное изменение амплитуд
.
Однако, принимая во внимание медленное изменение амплитуд ![]() , мы можем совершить указанный переход при
конечном периоде ЭМК. Для этого сделаем следующие замены:
, мы можем совершить указанный переход при
конечном периоде ЭМК. Для этого сделаем следующие замены:
![]() , (27)
, (27)
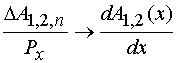 ,
,
Таким образом, мы приходим к системе двух нелинейных дифференциальных уравнений первого порядка:
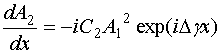 .
.
Система дифференциальных уравнений (28) отличается
от хорошо известной в теории нелинейных волн [2] системы, описывающей волны в
непрерывной нелинейной среде в режиме синхронизма сонаправленных волн только
разными знаками перед коэффициентами ![]() . Однако, это на первый
взгляд небольшое отличие существенно меняет характер решений системы (28).
. Однако, это на первый
взгляд небольшое отличие существенно меняет характер решений системы (28).
7. Квазисобственные волны ЭМК
Получим решение системы дифференциальных уравнений в виде собственной волны. Здесь необходимо отметить, что в нелинейных структурах понятие собственной волны играет совершенно другую роль, чем в линейных. В линейных системах справедлив принцип суперпозиции. Поэтому с помощью комбинации собственных волн можно описать произвольное поле внутри направляющей структуры. В нелинейном случае ситуация принципиально иная. Например, каждая волна может удовлетворять всем условиям задачи, а их сумма не будет являться ее решением. Также мы увидим, что параметры собственных волн зависят от условий их возбуждения, в отличие от линейной структуры, в которой они никак не связаны с источником возбуждения. Чтобы подчеркнуть отличие волн в нелинейном ЭМК от линейных волн, мы будем использовать термин квазисобственная волна.
Исследование квазисобственных волн не столь важно для дальнейшего анализа, как в линейном случае. Тем не менее, они являются частным интересным решением граничной задачи, который целесообразно изучить.
Введем новую
переменную ![]() :
:
![]() . (29)
. (29)
Тогда система (21) приобретет следующий вид:
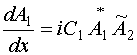 , (30)
, (30)
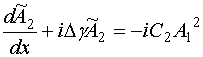 .
.
Ищем решение уравнений (30) в виде волны, распространяющейся в положительном направлении:
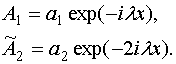 (31)
(31)
Подставим соотношения (31) в систему (30):
![]() , (32)
, (32)
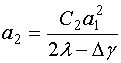 .
.
Из выражений (32)
видно, что зависимость от x устраняется только
для действительных постоянных ![]() .
.
Найдем
далее постоянную распространения ![]() , подставляя второе
уравнение (32) в первое:
, подставляя второе
уравнение (32) в первое:
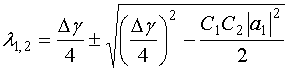 , (33)
, (33)
Отметим, что для волн, бегущих в противоположном направлении можно получить решение аналогичное (33), но с противоположным знаком.
Выражение, стоящее в
формуле (33) под радикалом может принимать как положительные, так и отрицательные
значения. При строгом выполнении условия синхронизма (![]() )
оно всегда отрицательно. Для отрицательных значений выражения под внутренним
радикалом формулу (33) можно переписать следующим образом:
)
оно всегда отрицательно. Для отрицательных значений выражения под внутренним
радикалом формулу (33) можно переписать следующим образом:
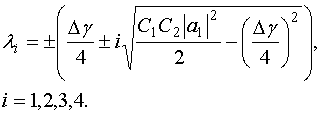 . (34)
. (34)
Таким образом, мы можем прийти к выводу, который пока является чисто формальным результатом, что синхронизм рассматриваемого типа ведет к появлению комплексных волн, у которых имеется затухание даже в структуре без тепловых потерь.
Отметим, что формула (33) дает нам четыре решения для постоянных распространения собственных волн. Будем классифицировать их в соответствии с правилом, описанным в разделе 3.
Появление комплексных
волн в линейных системах эквивалентно возникновению полосы запирания. Обычно
комплексные волны возбуждаются парами. При возбуждении ЭМК падающей из
полупространства ![]() волной пару образуют прямая
прямая и прямая обратная волны. Если у них одинаковые амплитуды, то вместе они
формируют стоячую волну, локализованную благодаря экспоненциальному затуханию
парциальных волн около места ее возбуждения. Стоячая волна представляет собой
колебание, в котором накапливается электромагнитная энергия. Возбуждение
подобного колебания сопровождается ростом коэффициента отражения вплоть до
единицы, что характерно для поведения ЭМК в полосе запирания.
волной пару образуют прямая
прямая и прямая обратная волны. Если у них одинаковые амплитуды, то вместе они
формируют стоячую волну, локализованную благодаря экспоненциальному затуханию
парциальных волн около места ее возбуждения. Стоячая волна представляет собой
колебание, в котором накапливается электромагнитная энергия. Возбуждение
подобного колебания сопровождается ростом коэффициента отражения вплоть до
единицы, что характерно для поведения ЭМК в полосе запирания.
В нелинейном ЭМК возникновение комплексных волн качественно должно приводить к аналогичным явлениям. К ним относятся затухающие по оси 0х распределения напряжений и токов в элементах ЭМК (аналог экспоненциально затухающих волн) и резонансный рост амплитуд волн отраженных от поверхности ЭМК.
Решение в виде
уединенной волны ставит важные вопросы. Один из них связан с нарушением
условий, при которых было получено соотношение (33) в полосе запирания, в
которой ![]() .
.
Другой
вопрос связан с присутствием в формуле для постоянной распространения
амплитудного множителя ![]() . Как понимать такую зависимость
даже за пределами полосы запирания, когда использование решения в виде
уединенной волны оправданно?
. Как понимать такую зависимость
даже за пределами полосы запирания, когда использование решения в виде
уединенной волны оправданно?
Обсуждение полученного выше решения начнем с наиболее простого вопроса о поведении квазисобственной волны в полосе пропускания, то есть при выполнении следующего неравенства:
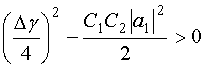 . (35)
. (35)
Единственным
необычным свойством квазисобственной волны в этом режиме является зависимость
ее постоянной распространения от амплитуды ![]() . В
рамках решения однородной системы уравнений, которая соответствует ЭМК без сторонних
источников амплитуда волны остается неопределенной. Для ее нахождения
необходимо ввести в структуру источник, который возбудит квазисобственную
волну.
. В
рамках решения однородной системы уравнений, которая соответствует ЭМК без сторонних
источников амплитуда волны остается неопределенной. Для ее нахождения
необходимо ввести в структуру источник, который возбудит квазисобственную
волну.
Таким
образом, параметр ![]() определяется источником,
локализованным в некоторой области пространства. В линейной системе параметры
волны, за исключением ее амплитуды, за пределами этой области зависят только от
свойств структуры, в которой она распространяется. Как видно из соотношения
(34), в нелинейном ЭМК волна сохраняет информацию об источнике возбуждения
также через свою постоянную распространения. Измеряя параметр
определяется источником,
локализованным в некоторой области пространства. В линейной системе параметры
волны, за исключением ее амплитуды, за пределами этой области зависят только от
свойств структуры, в которой она распространяется. Как видно из соотношения
(34), в нелинейном ЭМК волна сохраняет информацию об источнике возбуждения
также через свою постоянную распространения. Измеряя параметр ![]() на сколь угодно большом расстоянии от
точки возникновения волны, мы можем в принципе определить интенсивность
породившего ее источника.
на сколь угодно большом расстоянии от
точки возникновения волны, мы можем в принципе определить интенсивность
породившего ее источника.
Рассмотрим
далее поведение квазисобственной волны в полосе запирания. Как уже отмечалось
выше, полученное решение не может быть использовано в этом режиме, так как
амплитуда волны ![]() становится функцией постоянной
становится функцией постоянной ![]() , которая, в свою очередь, является
функцией амплитуды и т.д. Однако, при медленном изменении амплитуды, то есть
при малом значении
, которая, в свою очередь, является
функцией амплитуды и т.д. Однако, при медленном изменении амплитуды, то есть
при малом значении ![]() мы можем предположить, что
изменения модуля
мы можем предположить, что
изменения модуля ![]() описываются в рамках ВКБ
приближения:
описываются в рамках ВКБ
приближения:
![]() , (36)
, (36)
где ![]() ,
,
![]() .
.
Интегральное
уравнение (36) с помощью несложных преобразований, выполняемых с учетом
соотношения (34) сводится к дифференциальному уравнению относительно функции ![]() :
:
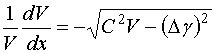 , (37)
, (37)
![]()
Решение уравнения (30) получаем аналитически в следующем виде:
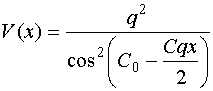 , (38)
, (38)
где ![]() -
постоянная интегрирования дифференциального уравнения (37). Ее можно найти из
концевого условия:
-
постоянная интегрирования дифференциального уравнения (37). Ее можно найти из
концевого условия:
![]() . (39)
. (39)
Под постоянной ![]() мы понимаем известную величину, равную
квадрату модуля амплитуды квазисобственной волны в точке ее возбуждения. С учетом
соотношения (39) находим выражение для
мы понимаем известную величину, равную
квадрату модуля амплитуды квазисобственной волны в точке ее возбуждения. С учетом
соотношения (39) находим выражение для ![]() :
:
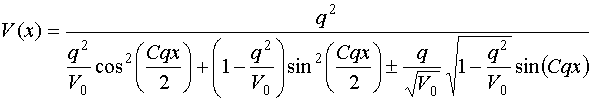 ,
,
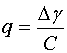 , (40)
, (40)
В формуле (40) необходимо выбирать положительный знак. При этом решение имеет убывающий характер. Отметим, что оно справедливо только в пределах полосы запирания. Условие ее существования дается неравенством:
![]() . (41)
. (41)
Таким образом, мы можем сделать вывод о том, что в рамках принятого приближения волна имеет убывающий характер, если в точке ее возбуждения выполняется очевидное неравенство:
![]() . (42)
. (42)
Далее по мере удаления от точки возникновения амплитуда волны убывает до тех пор пока не перестанет выполняться неравенство (41). После прохождения этой точки волна перестает быть затухающей. Она становится распространяющейся. Таким образом, эффект запирания имеет ограниченные пределы не только в частотном диапазоне, но и в пространстве.
Интересно получить
выражение для функции ![]() в приближении малого параметра
в приближении малого параметра ![]() . В этом приближении мы можем заменить в
формуле (40) тригонометрические функции алгебраическими:
. В этом приближении мы можем заменить в
формуле (40) тригонометрические функции алгебраическими:
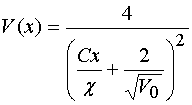 . (43)
. (43)
С помощью неравенства
(42) нетрудно определить координату ![]() , в которой происходит
выход из режима запирания:
, в которой происходит
выход из режима запирания:
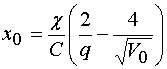 . (44)
. (44)
Из соотношения (44)
видно, что при ![]() координата
координата ![]() стремится к бесконечности. Таким образом,
при точном выполнении условия синхронизма волна не выходит из режима запирания.
стремится к бесконечности. Таким образом,
при точном выполнении условия синхронизма волна не выходит из режима запирания.
8. Генерация второй гармоники
Прежде чем перейти к решению системы
дифференциальных уравнений (28) для случая генерации второй гармоники получим
важное энергетическое соотношение, устанавливающее связь между модулями
амплитуд волн ![]() в режиме пространственного
синхронизма при
в режиме пространственного
синхронизма при ![]() . Для этого умножим первое
уравнение из (28) на
. Для этого умножим первое
уравнение из (28) на ![]() . Затем применим к первому
уравнению операцию комплексного сопряжения и умножим его на
. Затем применим к первому
уравнению операцию комплексного сопряжения и умножим его на ![]() . В результате получаем два уравнения:
. В результате получаем два уравнения:
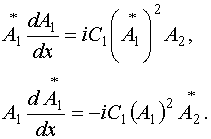 (45)
(45)
Сложим уравнения (45):
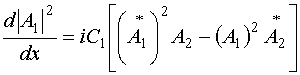 . (46)
. (46)
Проделаем аналогичные преобразования для второго уравнения из (28):
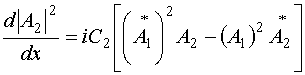 . (47)
. (47)
Из уравнений (46) и (47) следует искомое
соотношение для ![]() и
и ![]() :
:
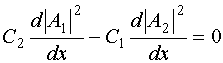 . (48)
. (48)
Схематично взаимодействие волн в режиме генерации второй гармоники показано на рис. 28.

Рис. 28. Схема возбуждения ЭМК в режиме генерации второй гармоники.
Слева на нелинейный ЭМК набегает волна на основной
частоте ![]() . Часть ее энергии преобразуется в
отраженную волну на частоте
. Часть ее энергии преобразуется в
отраженную волну на частоте ![]() , а часть в прошедшую
волну с частотой
, а часть в прошедшую
волну с частотой ![]() . Описанной схеме взаимодействия
волн соответствуют следующие концевые условия:
. Описанной схеме взаимодействия
волн соответствуют следующие концевые условия:
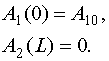 (49)
(49)
В формуле (49) ![]() -
величина, задаваемая источником возбуждения.
-
величина, задаваемая источником возбуждения.
Ищем решение системы (28) при ![]() в следующем виде:
в следующем виде:
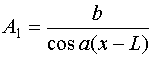 , (50)
, (50)
где ![]() - неизвестные
постоянные. Подставим выражение (50) во второе уравнение из (28):
- неизвестные
постоянные. Подставим выражение (50) во второе уравнение из (28):
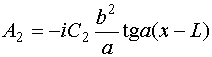 . (51)
. (51)
Далее подставим формулы (50) и (51) в первое уравнение из (28) и получим следующее соотношение:
![]() . (52)
. (52)
Решение для амплитуд ![]() имеет
следующий вид:
имеет
следующий вид:
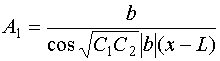 , (53)
, (53)
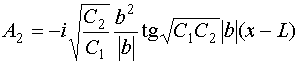 .
.
Постоянная ![]() находится
из концевых условий (49). Отметим, что условие для
находится
из концевых условий (49). Отметим, что условие для ![]() выполняется
автоматически. Поэтому нам необходимо удовлетворить только первому условию из
(49). В результате получаем:
выполняется
автоматически. Поэтому нам необходимо удовлетворить только первому условию из
(49). В результате получаем:
![]() . (54)
. (54)
Выражение (54) представляет собой трансцендентное
уравнение относительно постоянной ![]() , которое должно
решаться численно. Отметим, что решение (53) удовлетворяет соотношению (48).
, которое должно
решаться численно. Отметим, что решение (53) удовлетворяет соотношению (48).
Введем коэффициент преобразования волны основной
частоты в волны удвоенной частоты ![]() :
:
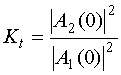 . (55)
. (55)
Для него справедливо соотношение:
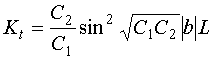 . (56)
. (56)
9. Параметрическое усиление первой гармоники
Схема возбуждения ЭМК в режиме параметрического усиления показана на рис. 29.

Рис. 29. Схема возбуждения ЭМК в режиме параметрического усиления.
Из нее следуют концевые условия для амплитуд ![]() :
:
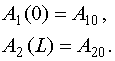 (57)
(57)
Найдем общее решение системы дифференциальных уравнений (28) приближенно, комбинируя два частных решения. Одно из них – это решение в гиперболических функциях, а другое – решение при постоянной накачке.
Решение в гиперболических функциях известно в теории нелинейных сред [2] для взаимодействия двух прямых волн. В случае распространения прямой и обратной волны это решение видоизменяется.
Для того, чтобы получить решение в гиперболических
функциях ищем амплитуду ![]() в следующем виде:
в следующем виде:
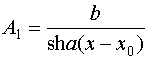 , (58)
, (58)
где ![]() и
и ![]() - постоянные, которые будут определены
ниже. Повторяя шаги, описанные в разделе 4, находим искомое решение:
- постоянные, которые будут определены
ниже. Повторяя шаги, описанные в разделе 4, находим искомое решение:
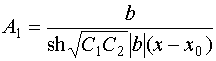 , (59)
, (59)
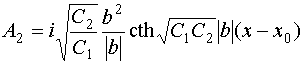 ,
,
![]() .
.
Из выражений (59) видно, что фазы амплитуд волн ![]() связаны с фазой
связаны с фазой ![]() постоянной
постоянной
![]() следующим образом:
следующим образом:
![]() , (60)
, (60)
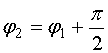 ,
,
Первое равенство (60) записано при условии ![]() .
.
Из формул (60) видно, что недостатком решения в
гиперболических функциях является фиксированная связь между фазами усиливаемой
волны ![]() и волны накачки
и волны накачки ![]() .
Поэтому с его помощью невозможно удовлетворить взятым в общем виде концевым
условиям (57).
.
Поэтому с его помощью невозможно удовлетворить взятым в общем виде концевым
условиям (57).
Для преодоления указанного недостатка рассмотрим
решение с заданной накачкой. Оно получается из первого уравнения (28) при
условии фиксированной величины ![]() . Схема решения не
отличается от аналогичного решения для двух прямых волн. Поэтому мы не будем
приводить его в деталях, а ограничимся конечным результатом:
. Схема решения не
отличается от аналогичного решения для двух прямых волн. Поэтому мы не будем
приводить его в деталях, а ограничимся конечным результатом:
![]() , (61)
, (61)
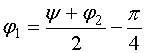 ,
,
![]() ,
,
где ![]() и
и ![]() - постоянные интегрирования
дифференциального уравнения.
- постоянные интегрирования
дифференциального уравнения.
Решение с заданной накачкой хорошо описывает взаимодействие волн при условии слабого влияния волны с основной частотой на волну накачки. Такое положение имеет место при усилении слабых сигналов, которые удовлетворяют следующему неравенству:
![]() . (62)
. (62)
Допустим, что источник возбуждения на основной частоте имеет существенно меньшую мощность источника накачки, то есть:
![]() .
.
В этом случае мы можем сделать вывод о том, что
решение с заданной накачкой хорошо описывает процесс при ![]() , то есть там, где волна основной частоты
усилена относительно слабо. Наоборот, при
, то есть там, где волна основной частоты
усилена относительно слабо. Наоборот, при ![]() мы
можем предположить, что для описания процесса взаимодействия волн подходит
решение в гиперболических функциях.
мы
можем предположить, что для описания процесса взаимодействия волн подходит
решение в гиперболических функциях.
Нам необходимо согласовать оба решения так, чтобы одно непрерывно переходило в другое. Кроме того, мы должны выполнить концевые условия. Решим обе поставленные задачи, выбирая постоянные, входящие в оба решения.
Рассмотрим условия при ![]() . По
нашему предположению в этой области справедливо решение в гиперболических функциях.
Поэтому мы можем записать:
. По
нашему предположению в этой области справедливо решение в гиперболических функциях.
Поэтому мы можем записать:
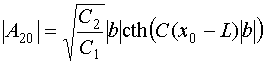 , (63)
, (63)
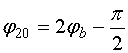 ,
,
![]() .
.
При записи выражений (63) мы предполагали, что ![]() . Первое соотношение из (63) является
трансцендентным уравнением относительно постоянных
. Первое соотношение из (63) является
трансцендентным уравнением относительно постоянных ![]() и
и ![]() . Из второго уравнения мы можем найти
. Из второго уравнения мы можем найти ![]() .
.
Перейдем к условиям при ![]() :
:
![]() , (64)
, (64)
![]() ,
,
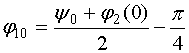 .
.
Найдем амплитуду второй волны на удвоенной частоте
при ![]() с помощью соотношений (59) и (63):
с помощью соотношений (59) и (63):
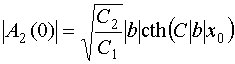 , (65)
, (65)
![]() .
.
Будем рассматривать случай ![]() .
При выполнении данного неравенства формула (64) приобретает новый вид:
.
При выполнении данного неравенства формула (64) приобретает новый вид:
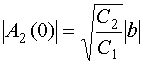 . (66)
. (66)
С помощью полученных соотношений мы можем записать
два выражения для амплитуды ![]() :
:
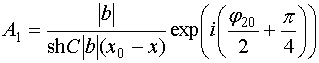 , (67)
, (67)
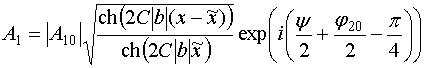 .
.
Первое равенство соответствует решению в
гиперболических функциях, а второе решению при заданной накачке. Получим
асимптотические выражения для амплитуды ![]() .
Считаем, что выполняются следующие неравенства:
.
Считаем, что выполняются следующие неравенства:
![]() , (68)
, (68)
![]() .
.
Если выполняются неравенства (68), то из выражений
(61) следует, что ![]() . Также из соотношений (68)
видно, что мы можем заменить гиперболические функции экспонентами:
. Также из соотношений (68)
видно, что мы можем заменить гиперболические функции экспонентами:
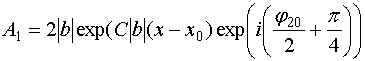 , (69)
, (69)
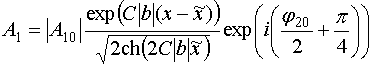 .
.
Из соотношений (69) следует, что фазы двух решений одинаковы. Модули также описываются экспонентами с одинаковыми показателями. Для полного совпадения решений необходимо приравнять множители, стоящие перед экспонентами:
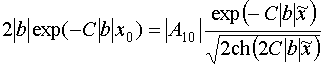 . (70)
. (70)
В уравнение (70) входят три неизвестные ![]() . Его необходимо дополнить двумя
уравнениями, следующими из соотношений (63) и (64):
. Его необходимо дополнить двумя
уравнениями, следующими из соотношений (63) и (64):
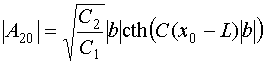 , (71)
, (71)
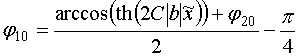 .
.
Уравнения (71) можно решить аналитически
относительно ![]() :
:
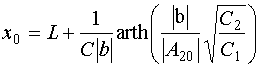 , (72)
, (72)
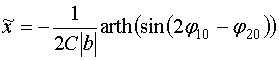 .
.
Уравнение (70) можно решить численно с учетом соотношений (72).
Подставим соотношения (72) в уравнение (70) с учетом выражений (64), (65):
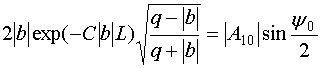 , (73)
, (73)
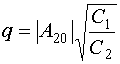 .
.
Для удобства исследования полученного уравнения введем следующие переменные:
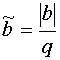 ,
,
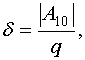
![]() . (74)
. (74)
Отметим, что новые параметры ![]() удовлетворяют неравенствам:
удовлетворяют неравенствам:
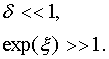 (75)
(75)
С новыми переменными уравнение (73) приобретает следующий вид:
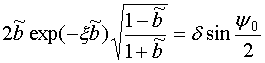 . (76)
. (76)
Графическое решение уравнения (76) поясняется на
рис. 30. Кривая 1 соответствует функции, стоящей в левой части (76), а кривая 2
в правой части. Видно, что кривые 1 и 2 пересекаются в двух точках,
соответствующих двум корням уравнения (76) ![]() .
Корень
.
Корень ![]() много меньше единицы. Поэтому данное
решение не удовлетворяет неравенствам (68). Сделанным выше допущениям
удовлетворяет корень
много меньше единицы. Поэтому данное
решение не удовлетворяет неравенствам (68). Сделанным выше допущениям
удовлетворяет корень ![]() .
.
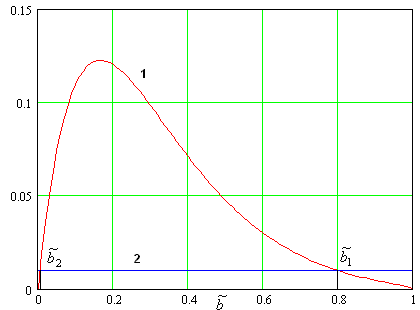
Рис. 30. Графическое решение уравнения.
Для количественного описания параметрического
усиления введем коэффициенты усиления и трансформации ![]() и
и
![]() следующим образом:
следующим образом:
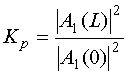 , (77)
, (77)
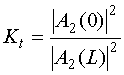 .
.
Для них справедливы соотношения:
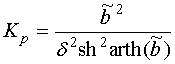 . (78)
. (78)
![]() .
.
Под ![]() в формулах (78)
понимается корень уравнения (76)
в формулах (78)
понимается корень уравнения (76) ![]() .
.
На рис. 31 и 32 показаны зависимости коэффициентов
![]() и
и ![]() от
параметра
от
параметра ![]() при разных
при разных ![]() .
Параметр
.
Параметр ![]() равен
равен ![]() .
Кривые 1 – 3 на рис. 31,32 получены при
.
Кривые 1 – 3 на рис. 31,32 получены при ![]() =0.0001,
0.0003, 0.001. Видно, что при относительно малых величинах
=0.0001,
0.0003, 0.001. Видно, что при относительно малых величинах ![]() коэффициент усиления, выраженный в
децибелах, растет линейно, что соответствует экспоненциальному росту амплитуды
первой гармоники. При дальнейшем увеличении
коэффициент усиления, выраженный в
децибелах, растет линейно, что соответствует экспоненциальному росту амплитуды
первой гармоники. При дальнейшем увеличении ![]() наблюдается
эффект насыщения, который выражается в появлении горизонтального участка кривых
1 – 3. Эффект насыщения сопровождается интенсивным преобразованием энергии
второй гармоники (см. рис. 32). На участке экспоненциального роста коэффициент
преобразования равен нулю децибел.
наблюдается
эффект насыщения, который выражается в появлении горизонтального участка кривых
1 – 3. Эффект насыщения сопровождается интенсивным преобразованием энергии
второй гармоники (см. рис. 32). На участке экспоненциального роста коэффициент
преобразования равен нулю децибел.
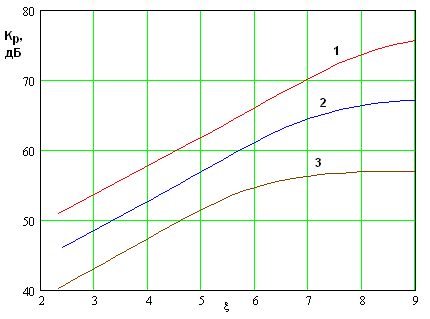
Рис. 31.
Зависимость коэффициента усиления от параметра ![]() .
.
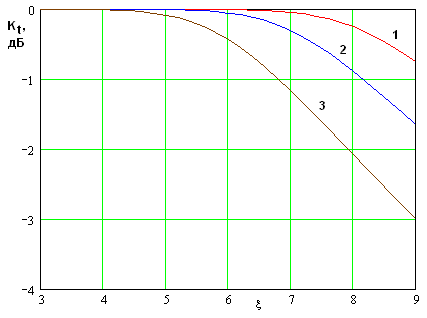
Рис. 32.
Зависимость коэффициента преобразования от параметра ![]() .
.
На рис. 33 показана зависимость коэффициента
усиления от параметра ![]() , который выражается через
разность начальных значений фаз
, который выражается через
разность начальных значений фаз ![]() . Видно, что
коэффициент усиления сильно зависит от этого параметра. При
. Видно, что
коэффициент усиления сильно зависит от этого параметра. При ![]() усиление отсутствует, а при
усиление отсутствует, а при ![]() =
=![]() оно
максимально. Зависимость коэффициента усиления от разности фаз возбуждающих
сигналов характерна для двухчастотного нелинейного взаимодействия [7].
оно
максимально. Зависимость коэффициента усиления от разности фаз возбуждающих
сигналов характерна для двухчастотного нелинейного взаимодействия [7].
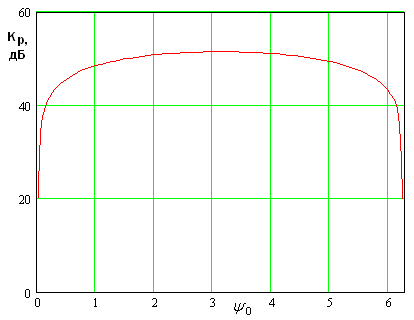
Рис. 33.
Зависимость коэффициента усиления от разности фаз ![]() .
.
Работа выполнена при поддержке Российского фонда фундаментальных исследований, проект № 11-08-00215-а.
Литература
1. Манцызов Б.И. Когерентная и нелинейная оптика фотонных кристаллов. М.: Физматлит. 2010.
2. Уизем Дж. Линейные и нелинейные волны. М.: Мир. 1977.
3. Сазонов В.П., Силин Р.А. Замедляющие системы. М.: Сов. Радио. 1966.
4. Банков С.Е. Полубесконечный нелинейный электромагнитный кристалл // Радиотехника и электроника. 2011. Т. 56. № 6. С. 613-621.
5. Банков С.Е. Модель нелинейного электромагнитного кристалла // Радиотехника и электроника. 2011. Т. 56. № 3. С. 1-14.
6. Шевченко В.В. Об обратных плоских волнах в однородных изотропных средах // Радиотехника и электроника. 2003. Т. 48. №10. С. 1202-1209.
7. Виноградова М.Б., Руденко О.В., Сухоруков А.П. "Теория волн", М.: Наука, 1990.