Research of Dynamic Characteristics in Radio system with Optimal Spatial Structure
S. I. Gusev, Yu. N. Parshin
Ryazan
State Radio Engineering University
Received April 25, 2013, after correction - September 3, 2013
Abstract. Increasing of radio-system noise immunity against spatially concentrated interference is achieved by optimizing the spatial processing which is an amplitude-phase forming on the array aperture with selection of the optimal spatial element position. To overcome the difficulties associated with increased optimal coordinate sensitivity to deviations of estimated non-stationary parameters, a regularized algorithm of robust spatial structure is used. A comparative analysis of the spatial processing efficiency in static and dynamic modes is carried out. High convergence speed of adaptive weight vector adjusting in spatially reconfigurable antenna arrays is achieved by pre-processing, which means changing spatial position of antenna array elements.
Keywords: optimization of spatial structure, adaptive signal-processing, preprocessing.
Introduction
The coordination of spatial structures of an observable field with spatial structures of radio system allows to increase interference immunity essentially [1,2]. At the same time high sensitivity of optimal spatial structures to deviations of field characteristics from the supposed ones does not allow to reach maximum interference immunity in case of non-stationary interferences, and accepted algorithms of optimization of spatial structure have low computing efficiency [3].
Grating lobes of antenna array pattern cause multiextremal criterion function with commensurable peaks [3,12], and refer a problem of synthesis optimal spatial structure to class of ill-conditioned problems as well. Strong dependence of optimal antenna element position on inaccuracy in initial data does not allow to apply directly interpolation methods for determination of antenna coordinates and leads to computing complexity increase. In previous paper regularized algorithms of spatial structure optimization for elimination of these disadvantages are offered [4]. This algorithm allows to synthesize robust spatial structures [5,6] with the size of the obtained spatial structure defined according to accepted metrics as the stabilizer is used [5]. As a result the effect of stabilization of optimal structure is found out in a static mode. It gives a possibility to raise computing efficiency by mean of interpolation methods in the case of calculation of antenna array coordinate.
Efficiency of spatial interference rejection considerably depends on properties of interference correlation matrix, particularly on its eigenvalues. For large difference of eigenvalues the convergence speed for gradient algorithms of adaptation decreases, and the sensitivity of matrix inversion result to errors of its estimation increases. This condition occurs if signal environment includes strong source of interference together with other weaker but nevertheless potent interference sources. This condition also obtains if two or more very strong interference sources arrive at the array from closely spaced directions [7].
Known methods of elimination of these drawbacks use various types of preprocessing: an accelerated gradient procedure [7], scaled conjugate gradient descent [8], cascade preprocessors with resolving the input signals into their eigenvector components. In this paper it is offered to implement preprocessing by variation of spatial structure of the receiving antenna array. Previously optimization of antenna array spatial structure was used for increase of signal-to-interference ratio [3], faster reorganization of spatial structure [9], optimization of non-linear signal processing in the presence of non-gaussian interferences [1,2].
Objective of the paper is the enhancement of adaptation speed for spatial interference compensation by means of preprocessing on the base of spatial structure optimization in antenna array.
1. Dynamic Properties of Radiosystem with Spatial Structure
Optimization in Presence of Interferences
1.1 Problem Statement
The research objective is to improve interference immunity of radiosystems with optimization of spatial structure in static and dynamic operating modes under the assumption of mechanical inertance of spatial structure tuning.
The discussed radiosystem
consists of an antenna array with amplitude-phase control. The
sum of the
determined desired signal and several point-source broadband gaussian
interferences is observed on an output of each antenna array element.
Interference immunity is defined as a signal-to-interference ratio on an output
of spatial processing system. The spatial structure is specified by a vector of
coordinates of antenna array elements ![]() .
Criterion function of spatial structure optimization is accepted as a
likelihood ratio
.
Criterion function of spatial structure optimization is accepted as a
likelihood ratio ![]() . The stabilizer is a size of
spatial structure
. The stabilizer is a size of
spatial structure ![]() [5], which is defined as a
distance of given spatial structure from some mid-point of this structure. A
measure of difference of one spatial structure
[5], which is defined as a
distance of given spatial structure from some mid-point of this structure. A
measure of difference of one spatial structure ![]() from
another
from
another ![]() is a metric
is a metric ![]() in
space of coordinates
in
space of coordinates ![]() of antenna elements on some
surface
of antenna elements on some
surface ![]() . The distance between two subsets from
this set is defined on set
. The distance between two subsets from
this set is defined on set ![]() as follows [5]:
as follows [5]:
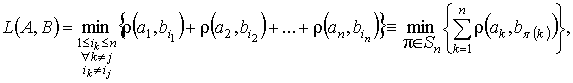
where ![]() - distance between
elements of coordinate subsets
- distance between
elements of coordinate subsets ![]() ,
, ![]() , and minimization is made on all
permutations from
, and minimization is made on all
permutations from ![]() elements of subset
elements of subset ![]() ;
; ![]() characterize
a position of
characterize
a position of ![]() -th spatial sample in
rectangular coordinate system. Hence a presence of distance
-th spatial sample in
rectangular coordinate system. Hence a presence of distance ![]() on set
on set ![]() transforms
it into metric space. The metrics
transforms
it into metric space. The metrics ![]() allows to solve a problem
of discrimination of spatial structures
allows to solve a problem
of discrimination of spatial structures ![]() .
.
Let an averaged likelihood ratio ![]() is a convex continuous function in some
neighbourhood, which has nonempty subset of points of minimum
is a convex continuous function in some
neighbourhood, which has nonempty subset of points of minimum ![]() . The stabilizer
. The stabilizer ![]() is
a strongly convex continuous function which characterize degree of difference
from a mid-point of spatial structure
is
a strongly convex continuous function which characterize degree of difference
from a mid-point of spatial structure 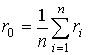 and
take on form
and
take on form 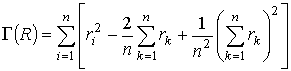 .
.
The regularized algorithm of spatial structure optimization looks as follows [5]:
![]() (1.1)
(1.1)
The
function ![]() is multiextremal in typical situations,
therefore in a range of definition
is multiextremal in typical situations,
therefore in a range of definition ![]() there can be some
points
there can be some
points ![]() ,
, ![]() , and
each ones has such neighbourhood
, and
each ones has such neighbourhood ![]() that there is
that there is ![]() , where
, where ![]() -
coordinates of the local minima, and one of which
-
coordinates of the local minima, and one of which ![]() is
coordinate of a global minimum:
is
coordinate of a global minimum:
![]() (1.2)
(1.2)
A search of the solution of multidimensional problem (1.2) is reduced to one-dimensional multistage problem solved by means of local extremum search methods [5,10,11]:
![]() ,
(1.3)
,
(1.3)
where
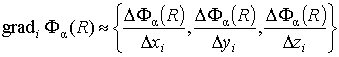 ,
,
![]() is a
antenna element number
is a
antenna element number ![]() is a step number,
is a step number, ![]() is convergence factor of gradient
algorithm. Thus, solving of a multiextreme problem is reduced to sequential
solving
is convergence factor of gradient
algorithm. Thus, solving of a multiextreme problem is reduced to sequential
solving ![]() local extremum problems (1.1) for all n
antenna elements. Iterative procedure (1.3) repeats while value of an error
local extremum problems (1.1) for all n
antenna elements. Iterative procedure (1.3) repeats while value of an error ![]() not above a preset value. After that
reduction twice of subarea
not above a preset value. After that
reduction twice of subarea ![]() is made, and
calculations repeat while the same requirement is met.
is made, and
calculations repeat while the same requirement is met.
1.2 Calculation Results
The analysis of optimization
algorithm (1.1)-(1.3) is carried out by means of computing experiment for a
case of the linear antenna array at number of interferences ![]() which are distributed uniformly in
angular sector size
which are distributed uniformly in
angular sector size ![]() =0,5 radian and located at an
angle
=0,5 radian and located at an
angle ![]() to a normal line of antenna plane. The
three-element antenna array is chosen, the distance between first and last
elements is fixed and is equals to 10
to a normal line of antenna plane. The
three-element antenna array is chosen, the distance between first and last
elements is fixed and is equals to 10![]() , and the medium
element is moveable.
, and the medium
element is moveable.
Estimation of synthesized topology is
carried out by means of analysis of occurrence frequency ![]() of distance
of distance ![]() when
random initial values
when
random initial values ![]() ,
, ![]() , with
uniform probability density function on
, with
uniform probability density function on ![]() . In
the absence of regularization there are some spatial structures
. In
the absence of regularization there are some spatial structures ![]() with commensurable frequencies of
occurrence for one position of signal and interferences. The regularization
factor increase to some critical value
with commensurable frequencies of
occurrence for one position of signal and interferences. The regularization
factor increase to some critical value ![]() gives
stability of solutions. Optimal structures slightly differ one from another
when changes of interference parameters is small and thereby this structure
become robust. Dependence
gives
stability of solutions. Optimal structures slightly differ one from another
when changes of interference parameters is small and thereby this structure
become robust. Dependence ![]() allows to define a
critical value of regularization parameter, providing stability of solution and
uniqueness of optimal spatial structure for various
allows to define a
critical value of regularization parameter, providing stability of solution and
uniqueness of optimal spatial structure for various ![]() . The
size of angular sector essentially influences on distance
. The
size of angular sector essentially influences on distance ![]() at
at ![]() :
increase of
:
increase of ![]() reduces influence of interferences on
spatial structure, and reduction of
reduces influence of interferences on
spatial structure, and reduction of ![]() increases distance
increases distance ![]() and size of the antenna aperture. The
reason for that is a necessity to increase angular resolution as signal source
is spaced nearer to interferences sources. Thus, application of regularization
provides uniqueness of solution for optimization procedure and provides its
poor sensitivity to initial conditions and to parameters of interferences as
well.
and size of the antenna aperture. The
reason for that is a necessity to increase angular resolution as signal source
is spaced nearer to interferences sources. Thus, application of regularization
provides uniqueness of solution for optimization procedure and provides its
poor sensitivity to initial conditions and to parameters of interferences as
well.
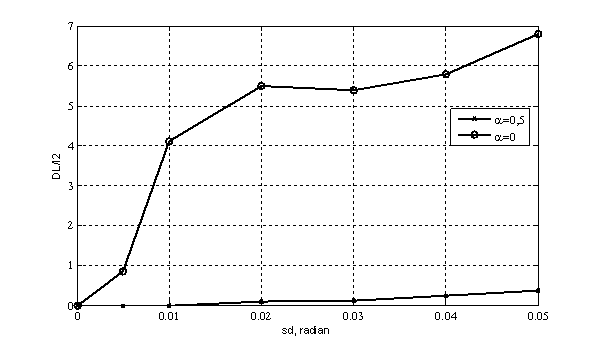
Figure 1
Regularization influence
on solution sensitivity to small deviations of interference spatial position is
presented on Figure 1. Dependence of a metric dispersion ![]() for accepted optimal structures on
root-mean-square deviation of interferences angular position
for accepted optimal structures on
root-mean-square deviation of interferences angular position ![]() with uniform distribution shows that
application of the stabilizer
with uniform distribution shows that
application of the stabilizer ![]() decreases metric
dispersion in 20 … 50 times and more.
decreases metric
dispersion in 20 … 50 times and more.
Calculation of dependence of normalized
signal-to-interference ratio ![]() on regularization
parameter
on regularization
parameter ![]() at various positions of interference
angular sector
at various positions of interference
angular sector ![]() is carried out, where
is carried out, where
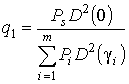 ,
, 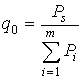
are
relations of signal power coming from direction ![]() , to
power of uncompensated interferences with and without taking into account the
directivity of the antenna array respectively,
, to
power of uncompensated interferences with and without taking into account the
directivity of the antenna array respectively, ![]() is
signal power,
is
signal power, ![]() ,
, ![]() are
power and angular coordinate of interference,
are
power and angular coordinate of interference, ![]() -
antenna array pattern. The analysis shows that
-
antenna array pattern. The analysis shows that ![]() grows as
grows as ![]() increase. This fact can be explained by increase of
signal and interferences spatial diversity. Efficiency gain from use of spatial
structure optimization is 9,8 dB in comparison with equidistant array at the
preset number of interferences and antenna elements.
increase. This fact can be explained by increase of
signal and interferences spatial diversity. Efficiency gain from use of spatial
structure optimization is 9,8 dB in comparison with equidistant array at the
preset number of interferences and antenna elements.
Continuous dependence of optimal element coordinates after synthesis of robust spatial structures, on spatial position of a signal and interferences allows to use interpolation methods for calculation intermediate values of coordinates at rather small number of interpolation points. The optimal structure is defined at interpolation points in advance for all combinations of power values and angular coordinates of the preset number of interferences. So the definition of optimum spatial structure in real time is possible as interpolation procedures possess high computing efficiency.
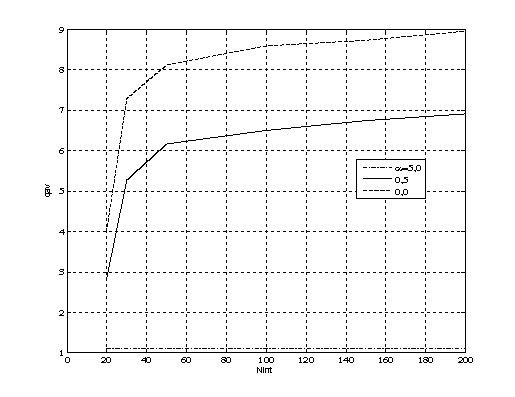
Figure 2
Dependence of
signal-to-interference ratio ![]() averaged by all
positions of interference sector
averaged by all
positions of interference sector ![]() on quantity of linear
interpolation points
on quantity of linear
interpolation points ![]() are represented on Figure 2
both with regularization and without of this one
are represented on Figure 2
both with regularization and without of this one ![]() .
Interpolation is applied to position of movable antenna element at change of
.
Interpolation is applied to position of movable antenna element at change of ![]() . Having set permissible
losses for signal-to-noise ratio, it is possible to define necessary number of
interpolation points for optimization procedure carrying out. So at reduction
of points number to
. Having set permissible
losses for signal-to-noise ratio, it is possible to define necessary number of
interpolation points for optimization procedure carrying out. So at reduction
of points number to ![]() at
at
![]() computing
complexity decrease not less than in 5 times under the set conditions of
modeling, and the general losses in comparison with maximum value of
signal-to-interference ratio efficiency-gain at
computing
complexity decrease not less than in 5 times under the set conditions of
modeling, and the general losses in comparison with maximum value of
signal-to-interference ratio efficiency-gain at ![]() make 1,7 dB in a static mode.
make 1,7 dB in a static mode.
Owing to interpolation, computing efficiency strongly increases at use of two-dimensional antenna arrays, at higher number of interferences in all forward hemisphere, at various level of power.
Mechanical element moving possesses noticeable inertance
which should be considered at the analysis of spatial optimization dynamic mode
at not-stationary interferences. Speed of spatial structure variation depend on
maximum possible change of element coordinate ![]() ,
expressed in wavelengths
,
expressed in wavelengths ![]() , for one time step of
spatial structure optimization system, and spatial non-stationarity of
interferences is set by interference angular sector moving
, for one time step of
spatial structure optimization system, and spatial non-stationarity of
interferences is set by interference angular sector moving ![]() for the same time interval.
for the same time interval.
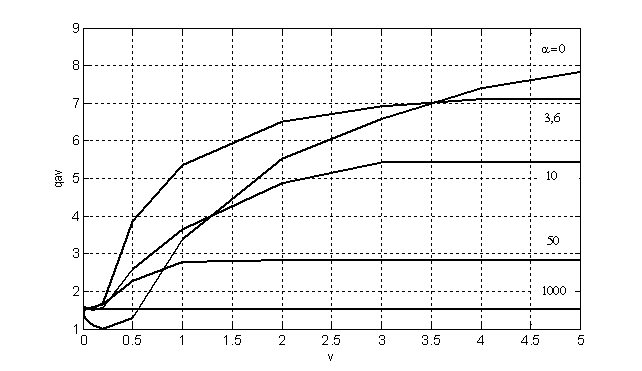
Figure 3
Research results are shown on Figure
3 in the form of dependence of signal-to-interference ratio ![]() averaged by
averaged by ![]() for
system with spatial structure optimization at dynamic operating mode. The analysis
was carried out by modeling at various values of regularization parameter
for
system with spatial structure optimization at dynamic operating mode. The analysis
was carried out by modeling at various values of regularization parameter ![]() at angular speed of interferences
at angular speed of interferences ![]() . It is the established fact that at
values of velocity parameter
. It is the established fact that at
values of velocity parameter ![]() l, regularization at
l, regularization at ![]() provides the maximum benefit in
interference immunity up to 6 dB in comparison with a case of spatial structure
optimization at a=0. Expansion of
signal-to-interference ratio averaging borders and increase in interference
movement velocity
provides the maximum benefit in
interference immunity up to 6 dB in comparison with a case of spatial structure
optimization at a=0. Expansion of
signal-to-interference ratio averaging borders and increase in interference
movement velocity ![]() expands parameter
expands parameter ![]() area which gives additional
signal-to-interference ratio gain.
area which gives additional
signal-to-interference ratio gain.
2. Enhancement of Adaptation Speed In Signal Processing System With Optimization Of Spatial Structure
2.1 System Model and Signal Processing
Let us consider an ![]() -element planar antenna
array with axial coordinates of elements
-element planar antenna
array with axial coordinates of elements ![]() . The
array is divided on two sub-arrays of
. The
array is divided on two sub-arrays of ![]() and
and ![]() elements respectively,
elements respectively, ![]() . The first sub-array of
. The first sub-array of ![]() elements
is intended for source direction finding and forms the main pattern. The
second sub-array of
elements
is intended for source direction finding and forms the main pattern. The
second sub-array of ![]() elements is intended for spatial interference compensation and contains
elements which provide the adaptive adjustment of amplitude and phases of
interferences. Coordinates of
elements is intended for spatial interference compensation and contains
elements which provide the adaptive adjustment of amplitude and phases of
interferences. Coordinates of ![]() elements can be
variable for obtaining of the best interference immunity.
elements can be
variable for obtaining of the best interference immunity.
Interference environment is set by ![]() point
sources with power
point
sources with power ![]() , allocated in the directions
set by angles of azimuth
, allocated in the directions
set by angles of azimuth ![]() and by angles of
elevation
and by angles of
elevation ![]() ,
, ![]() .
Vector of complex observable signal
.
Vector of complex observable signal ![]() represents a set of
complex envelopes for signal
represents a set of
complex envelopes for signal ![]() and interference
and interference ![]() on outputs of antenna elements at the
same point of time:
on outputs of antenna elements at the
same point of time:
![]() . (2.1)
. (2.1)
Matrix of spatial correlation for interferences on outputs of antenna elements:
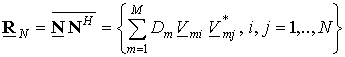 ,
(2.2)
,
(2.2)
where
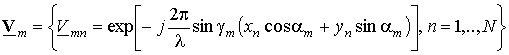 - interference source position vector,
which depends on antenna element coordinates, sign
- interference source position vector,
which depends on antenna element coordinates, sign ![]() denotes
Hermitian conjugation,
denotes
Hermitian conjugation, ![]() - wavelength.
- wavelength.
It is possible to represent signals on outputs of first and second sub-arrays as follows:
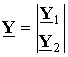 ,
,
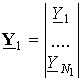 ,
, 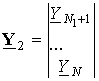 .
(2.3)
.
(2.3)
In this case correlation matrix has a block structure:
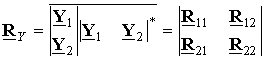 ,
,
and
optimal weight processing vector ![]() minimizes the power
of uncompensated residuals of interferences at
minimizes the power
of uncompensated residuals of interferences at ![]() =const
[7].
=const
[7].
Optimization of spatial structure of the second sub-array is carried out
by criterion (2.4) of maximum ratio of minimum ![]() and
maximum
and
maximum ![]() eigenvalues of matrix
eigenvalues of matrix ![]() , defining speed and stability of
adaptation process:
, defining speed and stability of
adaptation process:
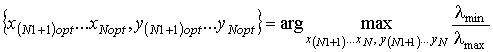 (2.4)
(2.4)
The criterion of maximum eigenvalues ratio allows to raise efficiency of interference rejection by solving the following problems:
- enhancement of convergence speed for the adaptive weight adjustment using gradient algorithms,
- reduction of correlation matrix inversion error,
- increase of suppression ratio by more exact nulling on antenna pattern.
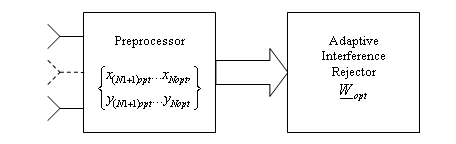

Figure 4.Spatial adaptive processing with spatial structure optimization
2.2 Numerical Analysis
Let us carry out the statistical modeling of preprocessing with optimization of spatial structure and processes in system with the adaptive spatial signal processing at various parameters of the antenna array ( Fig. 4).
For calculation of optimal vector value ![]() , where
, where ![]() - dispersion of estimation
error
- dispersion of estimation
error ![]() of the desired signal, we use a steepest
descent method [7]:
of the desired signal, we use a steepest
descent method [7]:
![]() ,
,
where ![]() - convergence factor,
- convergence factor, ![]() - interferences
suppression error.
- interferences
suppression error.
An
example of convergence result for weight ![]() adjustment
process in case of presence and absence of preprocessing with optimization of
space structure (2.4) is represented in Fig. 5. Modeling conditions:
interference-to-noise power ratio
adjustment
process in case of presence and absence of preprocessing with optimization of
space structure (2.4) is represented in Fig. 5. Modeling conditions:
interference-to-noise power ratio ![]() =20,
=20, ![]() =0,001,
=0,001, ![]() =2,
=2, ![]() , interferences angles of arrival
, interferences angles of arrival ![]() =25î,
=25î, ![]() =50î,
aperture size of array
=50î,
aperture size of array![]() .
.
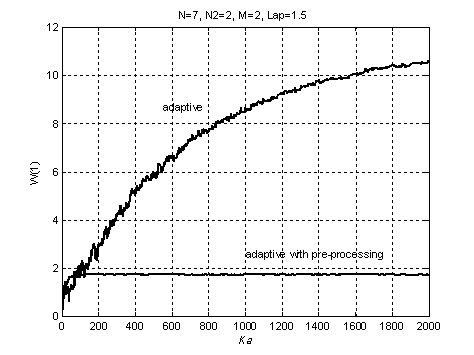
Figure 5. Adjustment of weight at adaptation with preprocessing
Fig.6 illustrates the same situation as the Fig.5 from the
point of antenna pattern nulling for adaptation with the preprocessor and
without it. In this case the number of adaptation steps ![]() =100 corresponds to time
of the preprocessing, which increase speed of convergence. Thus adaptive
antenna pattern with the preprocessing practically coincides with the optimal
one.
=100 corresponds to time
of the preprocessing, which increase speed of convergence. Thus adaptive
antenna pattern with the preprocessing practically coincides with the optimal
one.
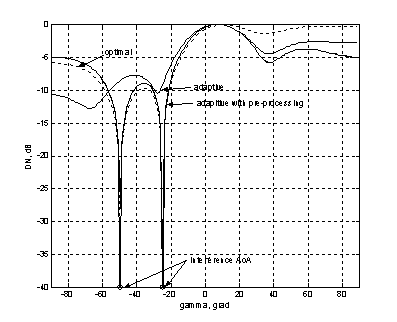
Figure 6. Antenna pattern nulling and adaptation with preprocessing
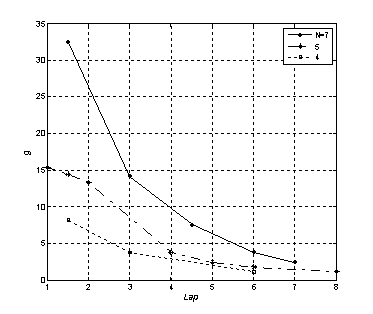
Figure 7. Dependence of minimum eigenvalues ratio on aperture size
The adaptation speed gain is illustrated by dependences of minimum optimal eigenvalues to original eigenvalues ratio
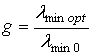
on aperture size ![]() of original uniformly spaced antenna
array, Fig. 7. It is necessary to mark that maximum gain of adaptation speed is
reached in the cases of small sizes of the antenna array aperture.
of original uniformly spaced antenna
array, Fig. 7. It is necessary to mark that maximum gain of adaptation speed is
reached in the cases of small sizes of the antenna array aperture.
Conclusion
Thus regularized algorithm of spatial structure optimization provides poor sensitivity signal-to-interference ratio to deviations from suppositions, and the introduced stabilizer limits the size of spatial structure. It is shown that optimal spatial structures, obtained as a result of regularization, possess stability both to deviations of antenna element initial positions and to change of signal and interference positions. These properties of optimal structures allow to solve a number of technical problems facing before developers of radiosystems. For example, for increase of computing efficiency there is possibility to use interpolation of optimal structures for the values calculated in advance and stored in database. Other advantage of regularized spatial structure optimization algorithms is continuous dependence of antenna element coordinates on parameters of interferences that allows to lower requirements to velocity of reorganization and, thus, to establish optimum coordinates of elements more precisely, to increase signal-to-interference ratio in comparison with absence of regularization.
Moreover, in this paper preprocessing in the form of spatial structure optimization in antenna array is proposed. Efficiency of the method of convergence improvement for adaptive adjustment process of weight vector is shown. Increase of efficiency of point-source interferences suppression by means of more exact and fast nulling on antenna pattern is also obtained. Maximum gain in adaptation speed is reached at the small sizes of the antenna array aperture and increased up to 32 times under predetermined conditions modeling.
References
1. Parshin Yu.N., Gusev S.I. Optimal receiving discrete messages by means of development systems with optimal spatial structure// Radio engineering and electronics, 2000, V. 45, ¹3, pp. 305-312.
2. Parshin Yu.N., Gusev S.I. Optimization of spatial structure in radiosysytem with nonlinear interference compensation // Radioengineering, TV and Communications. – Murom: VLGU, 1999, pp.112-116.
3. Parshin Yu.N., Gusev S.I. Influence of signal and interference positions on optimal spatial structure of antenna system // Bulletin of Ryazan state radio engineering academy, Ryazan: RGRTA , 1998, V.4, pp. 117-120.
4. Tikhonov A.N., Arsenin V.Ya. Methods of Solving Ill-posed Problems - M.: Nauka, 1986.
5. Parshin Yu. N., Lavrov A.M., Gusev S.I. Synthesis of robust spatial structures of radiosystems with use of regularization // Bulletin of Ryazan state radio engineering academy, Ryazan: RGRTA, 2000, V.6, pp. 11-14.
6. Parshin Yu. N., Gusev S.I. Synthesis of regularized algorithm for robust spatial structures of radiosystems // 3-rd International Conference “DSPA-2000”, Moscow: MCNTI, 2000, V2, pp.-26-29.
7. R.A. Monzingo, T.W. Miller. Introduction to Adaptive Arrays. Wiley, New York, 1976.
8. L.Hasdorf. Gradient Optimization and Nonlinear Control. Wiley, New York, 1976, Ch.3
9. Yu. N. Parshin, S. I. Gusev. Dynamic Mode of Radiosystem with Spatial Structure Optimization in Presence of Interferences// 4-th MicroWave and Radar Week, MRW-2010, 18th International Conference on Microwave Radar and Wireless Communications, MIKON-2010, Vilnius, Lithuania, June 14-16, 2010, V. 1, GEOZONDAS Ltd, 2010, p.p.133-136.
10. Strongin R.G. Numeric methods in multiextreme problems. – M.: Nauka, 1978.
11. Vasiliev F.P. Methods of extreme problems solving. - M.: Nauka, 1981.
12. Parshin Yu. Signal detection in the presence of space interferences with using space structure optimization and sequential samples // International radar symposium 2007 – IRS 2007, Cologne, Germany. Proceedings. – German institute of navigation, 2007. – pp. 451-454.