UDC 517, 519.642, 535.4, 621.372.8
INTRODUCTION TO THE ANALYSIS OF THE BIFURCATION PHENOMENA IN AN OPTICAL WAVEGUIDE WITH
STATISTIC IRREGULARITIES
Alexandre A. Egorov
A.M. Prokhorov’ General Physics Institute of the Russian Academy of Sciences
Received: September 18, 2013
Abstract: The theoretical principles of a new method of a research of irregular multimode optical waveguides as nonlinear dynamic dissipative systems are presented. The scattering of a guided mode is considered as process of gradual transition of some dynamic dissipative system from an “ordered” state in a state of “chaos”. The growth of losses on scattering in an irregular integrated-optical waveguide is considered as increase of chaos in a system. As a managing parameter of process the factor of phase slowing down of a waveguide is used.
Keywords: optical waveguide, guided and radiation modes, statistical irregularities, waveguide scattering, nonlinear equation, bifurcation phenomena nonlinear dynamic system, dissipative system, numerical simulation.
1. Introduction
Process of scattering of a directed mode in an irregular
optical waveguide can be considered as a process of the gradual transition of a
certain dynamic dissipative (open) system from an “ordered” state in a state of
“chaos”. We use as the controlling parameter of this process the factor of
phase slowing ![]() of a multimode waveguide (as
of a multimode waveguide (as ![]() changes with time, the effective
thickness of a waveguide varies) which is the natural physical parameter of system.
changes with time, the effective
thickness of a waveguide varies) which is the natural physical parameter of system.
We define the ordered state of a research system as the state when an irregular optical waveguide supports some directed mode (a regular component), and the contribution of radiation modes (an irregular component) to the distribution of the full field of a waveguide is negligible small. The state of chaos, on the contrary, is characterized by the essential contribution of radiation modes to the distribution of the full waveguide field.
2. Analysis of bifurcation phenomena in an optical waveguide with statistic irregularities
The
analysis of transition of an irregular integrated-optical waveguide from an ordered
state in a chaotic i.e. disordered state is carried out qualitatively with the
help of the diagram of wave numbers [1] combined with a dependence of attenuation
coefficient of waveguide's modes on the factor ![]() (see fig.
1) [2-4].
(see fig.
1) [2-4].
Consider a small (compared with the thickness ![]() of the waveguide) solitary jump
of the waveguide) solitary jump ![]() in a certain section of the waveguide
under study, which meet the condition
in a certain section of the waveguide
under study, which meet the condition ![]() . To
calculate the integral power losses
. To
calculate the integral power losses ![]() (attenuation
coefficient of the guided mode on a section of length
(attenuation
coefficient of the guided mode on a section of length ![]() )
due to scattering in this section, we can use the expression [3]:
)
due to scattering in this section, we can use the expression [3]:
![]() ,
(1)
,
(1)
where
![]() is the total power of the guided mode incident on the
waveguide section under consideration;
is the total power of the guided mode incident on the
waveguide section under consideration; ![]() is the relative
power losses;
is the relative
power losses; ![]() and
and ![]() are the amplitude
(dimensionless) coefficients of transmission and reflection of the guided mode
at the given section of the waveguide.
are the amplitude
(dimensionless) coefficients of transmission and reflection of the guided mode
at the given section of the waveguide.
Taking into account ![]() = 0 (the analogous result
can be obtained for
= 0 (the analogous result
can be obtained for ![]() = 0), expression Eq. (1) can be rewritten
in the form, well known in the theory of nonlinear dynamic systems [2-5]:
= 0), expression Eq. (1) can be rewritten
in the form, well known in the theory of nonlinear dynamic systems [2-5]:
![]() ,
(2)
,
(2)
where
![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() for example.
for example.
Eq. (2) can be rewritten then in the well-known form [5] that
is nonlinear with respect to the variable ![]() :
:
![]() .
(3)
.
(3)
By virtue of definition of coefficient ![]() ranges of variation of
ranges of variation of ![]() and
and ![]() in
Eqs. (2), (3) are obviously limited:
in
Eqs. (2), (3) are obviously limited: ![]() ,
, ![]() .
.
We will show that increase of chaos in system (growth of
scattering losses in an irregular waveguide with excitation of modes of more
and more high order) may be explained by a sequence of direct bifurcations (for
example, existence in system of stable cycles ![]() ,
, ![]() ,… [2-4].
,… [2-4].
In our case, the variable ![]() (attenuation
coefficient
(attenuation
coefficient ![]() ), depends both on the factor
), depends both on the factor ![]() and on the correlation interval
and on the correlation interval ![]() of the waveguide irregularities. In the
numerical simulation, we fix one parameter, for example
of the waveguide irregularities. In the
numerical simulation, we fix one parameter, for example ![]() ,
and consider the dependence of the function
,
and consider the dependence of the function ![]() on the
second parameter, i.e., on
on the
second parameter, i.e., on ![]() .
.
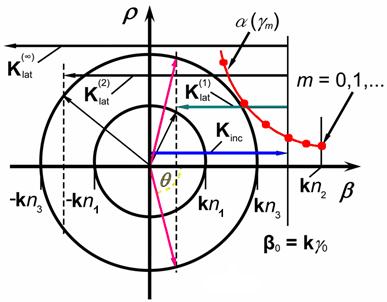
Fig. 1. The diagram of wave numbers combined with dependence
of an attenuation factor ![]() of waveguide's modes on the factor of phase slowing
of waveguide's modes on the factor of phase slowing ![]() :
: ![]() ;
; ![]() is the number of the guided mode;
is the number of the guided mode; ![]() is the factor of phase slowing for the
fundamental mode;
is the factor of phase slowing for the
fundamental mode; ![]() is the scattering angle of the
radiation modes;
is the scattering angle of the
radiation modes; ![]() is the propagation constants of
a guiding or radiation modes;
is the propagation constants of
a guiding or radiation modes; ![]() ;
; ![]() are refractions indices of covering
medium (air), waveguide layer and substrate accordingly,
are refractions indices of covering
medium (air), waveguide layer and substrate accordingly, ![]() ;
; ![]() ;
; ![]() is the module of lattice vector in the
irregularities spectrum.
is the module of lattice vector in the
irregularities spectrum.
As an example, the cycles ![]() are
shown on fig. 2. In this case, the convergence of process of some any index
points to some constant values of independent variables is visible. Note that
factor
are
shown on fig. 2. In this case, the convergence of process of some any index
points to some constant values of independent variables is visible. Note that
factor ![]() (called sometimes the effective waveguide
refraction index) shows how many times the phase velocity of the wave
propagating along the waveguide is smaller than the velocity of this light in
vacuum.
(called sometimes the effective waveguide
refraction index) shows how many times the phase velocity of the wave
propagating along the waveguide is smaller than the velocity of this light in
vacuum.
In this case, one can see the convergence of a process to ![]() or to
or to ![]() , which
are some characteristic parameters of a statistical irregularity of considered
dynamic system at preset values of operating parameter
, which
are some characteristic parameters of a statistical irregularity of considered
dynamic system at preset values of operating parameter ![]() .
.
Thus, if the assumption of independence of statistic
components of irregularity is carried out, the result received here quite
corresponds to the conclusion that the sum of the big number of these addendums
according to the central limiting theorem is distributed under the Gauss law
with the correlation radius and root-mean-square height of the profile,
determined as average on ensemble (and characteristic for the given wavelength
of laser radiation ![]() ) and close to
) and close to ![]() .
.
Using methods of the catastrophe theory [5], we shall explain
character of behavior of the examined dissipative system when controlling
parameters varies. We use for this purpose the diagram of the first derivative of
non-smoothed and smoothed dependences of relative power losses ![]() on
on ![]() due to
scattering established with the help of numerical differentiation (see fig. 3).
due to
scattering established with the help of numerical differentiation (see fig. 3).
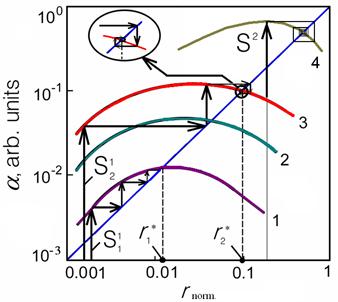
Fig.
2.
Dependence of relative losses of radiation power on the normalized correlation
radius, describing process of bifurcations (cycles ![]() and
and ![]() ) in an asymmetrical waveguide (
) in an asymmetrical waveguide (![]() = 1.000,
= 1.000, ![]() =
1.590,
=
1.590, ![]() = 1.460, all for
= 1.460, all for ![]() =
0.63 μm). The factor
=
0.63 μm). The factor ![]() for curves is equal: 1
– 1.570, 2 – 1.500, 3 – 1.470, 4 – 1.480.
for curves is equal: 1
– 1.570, 2 – 1.500, 3 – 1.470, 4 – 1.480.
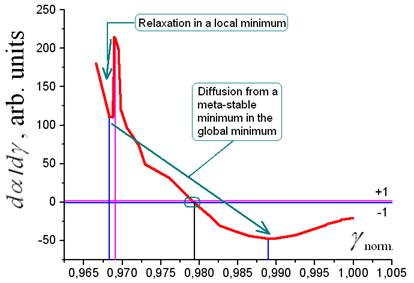
Fig. 3. The diagram of dependence of the
first derivative of relative radiation power losses on ![]() .
.
This function ![]() (which by analogy to
the theory of catastrophes can be considered as some potential function of
system) has a local minimum at the relative value
(which by analogy to
the theory of catastrophes can be considered as some potential function of
system) has a local minimum at the relative value ![]()
![]() 0.968, and they have sequentially a
global minimum at
0.968, and they have sequentially a
global minimum at ![]()
![]() 0.989,
and a maximum at
0.989,
and a maximum at ![]()
![]() 0.969
(see fig. 3). In the interval marked by two horizontal lines “+1” and “-1”, the
condition of stability of special points
0.969
(see fig. 3). In the interval marked by two horizontal lines “+1” and “-1”, the
condition of stability of special points ![]()
![]() 0.978 is observed, here:
0.978 is observed, here: ![]()
![]() 1.
This interval defines a region of values of function where the module of the
first derivative does not exceed 1.
1.
This interval defines a region of values of function where the module of the
first derivative does not exceed 1.
We can explain these peculiarities of as follows. The maximum
determines height of a barrier, which system is necessary overcoming to pass
from a local minimum in global, or back. A local minimum of function in area of
a point ![]()
![]() 0.968 at the exact
entrance data and absence of other errors, undoubtedly, there will be
insignificant, however a global minimum at
0.968 at the exact
entrance data and absence of other errors, undoubtedly, there will be
insignificant, however a global minimum at ![]()
![]() 0.989 it will obviously be kept always.
The dependence
0.989 it will obviously be kept always.
The dependence ![]() is similar to a well-known case
of a bifurcation of a state of equilibrium (“particle” in a potential pit with
a barrier or shelf).
is similar to a well-known case
of a bifurcation of a state of equilibrium (“particle” in a potential pit with
a barrier or shelf).
When processing the experimental data, especially in a case
of the low SNR it is necessary very accurately to apply the given approach to
the analysis of an irregular optical waveguide as a dissipative dynamic system.
Conditions at which the system leaves one equilibrium (metastable) state and
begins to pass in another metastable or stable equilibrium, depends on noise
level in system. At the high signal-to-noise ration, only one state of equilibrium
of system is possible: at ![]()
![]()
![]()
![]() 0.978 (see fig. 3). It
is possible to apply here the concept of phase transition where there is a
qualitative change of system. For example, at
0.978 (see fig. 3). It
is possible to apply here the concept of phase transition where there is a
qualitative change of system. For example, at ![]()
![]()
![]() or
or ![]()
![]()
![]() the
minimal losses are in system and a waveguide almost does not radiate (enclosed
system), i.e. it is not observed in environment (since the track of a mode is
not seen), and at
the
minimal losses are in system and a waveguide almost does not radiate (enclosed
system), i.e. it is not observed in environment (since the track of a mode is
not seen), and at ![]()
![]()
![]() the system passes in qualitatively new state:
the waveguide radiates (open system) and the track of a mode is seen. In other
words it is possible to tell, that at
the system passes in qualitatively new state:
the waveguide radiates (open system) and the track of a mode is seen. In other
words it is possible to tell, that at ![]()
![]()
![]() or
or ![]()
![]()
![]() the
irregularity actually is not evident in system (there are few radiation in the
framing medium), and at
the
irregularity actually is not evident in system (there are few radiation in the
framing medium), and at ![]()
![]()
![]() the irregularity of a waveguide is evident
as much as possible (there is a maximal radiation in the covering medium). From
the physical point of view the dissipativity of an irregular optical waveguide
means, that all “movements” with enough big energy (here: energy of radiation) damp
in system and system “tends to” to proceed in energetically more favorable state
of a global minimum at
the irregularity of a waveguide is evident
as much as possible (there is a maximal radiation in the covering medium). From
the physical point of view the dissipativity of an irregular optical waveguide
means, that all “movements” with enough big energy (here: energy of radiation) damp
in system and system “tends to” to proceed in energetically more favorable state
of a global minimum at ![]()
![]() 0.99 (
0.99 (![]()
![]() 1.55),
which is characterized by small enough losses on radiation [2-4].
1.55),
which is characterized by small enough losses on radiation [2-4].
Thus, it is possible to consider dissipative system i.e. an
irregular optical waveguide as a system where energy of the ordered process,
namely process of waveguide's propagation of a directed mode, passes into energy
of the disorder process (process of scattering), i.e. in energy of radiation modes,
and, finally, in thermal energy. It is evidently possible to demonstrate this
phenomenon, if in a multimode irregular waveguide to excite simultaneously
(spatial scanning instead of time scanning) a quantity of modes so that they
can propagate at different angles to an axis z in the plane of waveguide.
Then according to the previously mentioned, the greatest track (the minimal
losses on radiation) it is necessary to expect for a mode with ![]()
![]() 1.55.
We shall notice, that on Tien’s method it is necessary, that the minimal losses
on radiation will be for a mode with
1.55.
We shall notice, that on Tien’s method it is necessary, that the minimal losses
on radiation will be for a mode with ![]()
![]() 1.59,
as from the optical-beam point of view a beam (or plane partial wave, i.e. the Brillouin’s
wave) corresponding to a mode incident on boundary of the waveguide media at an
angle to close to the angle of mirror reflection. However, Tien’s method is
based on Rayleigh criterion [1] that does not take into account the waveguide's
character of light scattering, well confirmed in practice [1, 6]. However, it
is difficultly realized it experimentally at values γ close to
boundary values:
1.59,
as from the optical-beam point of view a beam (or plane partial wave, i.e. the Brillouin’s
wave) corresponding to a mode incident on boundary of the waveguide media at an
angle to close to the angle of mirror reflection. However, Tien’s method is
based on Rayleigh criterion [1] that does not take into account the waveguide's
character of light scattering, well confirmed in practice [1, 6]. However, it
is difficultly realized it experimentally at values γ close to
boundary values: ![]() = 1.46 and
= 1.46 and ![]() = 1.59. We shall consider in detail only
the second case as the first is similar to the second.
= 1.59. We shall consider in detail only
the second case as the first is similar to the second.
It is impossible to realize a waveguide's regime at ![]()
![]() 1.59 (
1.59 (![]() = 1.59), since in this case the wave is propagated
with phase speed equal to the speed of light in the environment with the refraction
index equal to a refraction index of the waveguide's layer
= 1.59), since in this case the wave is propagated
with phase speed equal to the speed of light in the environment with the refraction
index equal to a refraction index of the waveguide's layer ![]() , and, hence, this wave is propagated in “waveguide”
with (indefinitely) big thickness (a wave is not “sensitive” to boundaries). Then
this plane wave (not limited beam) should have indefinitely big energy in an
infinite cross plane “waveguide” in order that its amplitude was identical
overall infinite plane (a plane of equal amplitudes). The analogous result
takes place in a case of white noise for which the full power of a process is
infinite. Let's note, that the concept of a plane wave is usually used widely
enough in physics, however thus, as a rule, the power aspect is mentioned only
after traversing by a plane wave of an aperture in the screen (diffraction phenomenon),
after incidence of a plane wave on boundary of the unit of media with different
refraction indexes when the phenomenon of full internal reflection is observed and
the refracted wave becomes non-uniform etc. In all these cases there is an
opportunity to use integration in final limits only after interaction of a plane
wave with object, otherwise the integral will be divergent.
, and, hence, this wave is propagated in “waveguide”
with (indefinitely) big thickness (a wave is not “sensitive” to boundaries). Then
this plane wave (not limited beam) should have indefinitely big energy in an
infinite cross plane “waveguide” in order that its amplitude was identical
overall infinite plane (a plane of equal amplitudes). The analogous result
takes place in a case of white noise for which the full power of a process is
infinite. Let's note, that the concept of a plane wave is usually used widely
enough in physics, however thus, as a rule, the power aspect is mentioned only
after traversing by a plane wave of an aperture in the screen (diffraction phenomenon),
after incidence of a plane wave on boundary of the unit of media with different
refraction indexes when the phenomenon of full internal reflection is observed and
the refracted wave becomes non-uniform etc. In all these cases there is an
opportunity to use integration in final limits only after interaction of a plane
wave with object, otherwise the integral will be divergent.
The similar result is obtained in the first case, when ![]() = 1.46, as in this case the plane wave is
propagated with phase speed which is equal to speed of light in the environment
with the refraction index equal to the refraction index of a substrate (the
wave is propagated in “waveguide” with practically zero thickness). From this
point of view, we also interpret as energetically more favorable state of a
global minimum at
= 1.46, as in this case the plane wave is
propagated with phase speed which is equal to speed of light in the environment
with the refraction index equal to the refraction index of a substrate (the
wave is propagated in “waveguide” with practically zero thickness). From this
point of view, we also interpret as energetically more favorable state of a
global minimum at ![]()
![]() 0.99.
0.99.
With the help of a sequence of cycles
![]() ,
, ![]() , … it
is possible to show, that acyclic, statistic process arises as a limit of more
and more complex structures (cycles
, … it
is possible to show, that acyclic, statistic process arises as a limit of more
and more complex structures (cycles ![]() ). Occurrence of a
strange attractor can be explained with the help of cycle
). Occurrence of a
strange attractor can be explained with the help of cycle ![]() describing chaos in system. In this case,
“time” ways of two close points quickly miss current, and it is impossible to
predict behavior of researched system (the chaos becomes more statistic).
describing chaos in system. In this case,
“time” ways of two close points quickly miss current, and it is impossible to
predict behavior of researched system (the chaos becomes more statistic).
3. Conclusion
In the presented paper, we have schematically outlined new principles of research of irregular optical waveguides as a dynamic dissipative system. This approach may become especially perspective for the qualitative analysis of scattering in waveguides with complex topology of elements when application of analytical and computing methods is impossible. Besides it is doubtless, represents fundamental and applied interest application of this method at research of the phenomenon of abnormal scattering of light near to points of phase transitions in liquid and (poly-) crystal waveguide's layers. Special interest represents research in the area of a waveguide's rainbow where the thin structure of a spectrum of the light scattered in an irregular waveguide may be observed with high resolution.
It is natural, that in process of a transition from a waveguide with a simple irregularity (e.g. a harmonious grating) to a waveguide with statistical irregularities, the level of a continuous noisy component will accrue, absorbing sub harmonic components. Decrease of chaos in system at values of factor of phase delay less than some critical may be explained by the return bifurcation translating system in a state of ordered. Transition from an integrated-optical waveguide with an irregularity such as a harmonious grating to a waveguide with statistical irregularities (i.e. transition from system with the distant order to system with the near order) may be illustrated on a phase plane as transition from the system characterized by a usual attractor (stable focus in system with losses), to the system characterized by a stochastic attractor (drawing set of unstable trajectories in space of states of dissipative system). This transition is similar to transition from the ordered phase state in disorder. Here there is some analogy to loss of stability by a crystal when returning force disappears at the certain distortions of a crystal lattice at temperature of phase transition.
This phenomenon and the phenomenon of abnormal scattering of the light near to points of phase transitions in liquid waveguide's layers represents now at all not investigated area of knowledge standing at the border of the integrated optics, solid-state physics, nanoelectronics, physics of liquid, biophysics and spectroscopy.
1. Barnoski M.K. (Ed.) Introduction to Integrated Optics (New York: Plenum Press, 1974).
2. Egorov A.A. The bifurcation phenomena in planar optical waveguides with statistical irregularities, Proc. of the VIIth International Conf. “Lasers in Science, Engineering, Medicine”, 24 – 26 September, Russia (Moscow: IRE RAS, 1996, pp. 97-99).
3. Egorov A.A. Study of bifurcation processes in a multimode waveguide with statistical irregularities, Quantum Electronics. 2011, V. 41, No. 10, pp. 911-916.
4. Egorov A.A. Fundamentals of the theoretical analysis of irregular integrated- optical waveguides as nonlinear dynamic dissipative systems, Proc. of the Conf. “Methods of mathematical physics and mathematical modeling of physical processes”, Scientific Session MEPHI-2013, Moscow, Russia, 1 – 6, February 2013 (Moscow: National Research Nuclear University “MEPhI”, 2013, V. 3. P. 129).
5. Gilmore R. Catastrophe theory for science and engineers (New York: Wiley, 1981).
6. Hunsperger R.G. Integrated Optics. Theory and Technology (New York: Springer-Verlag, 1984).