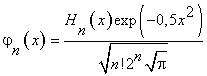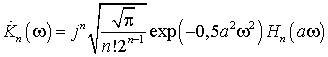УДК: 621.37,51-74
Построение ортогонального банка фильтров на основе преобразований Эрмита для обработки сигналов
Д. А. Балакин, В. В. Штыков
Национальный исследовательский университет «МЭИ»
Статья получена 27 августа 2014 г.
Аннотация. В работе излагаются принципы построения ортогонального банка фильтров на основе преобразований Эрмита. Осуществляется проверка работоспособности разработанного алгоритма фильтрации на моделях последовательности импульсов, состоящих из суммы функций Эрмита различных порядков. Продемонстрировано выделение локальных особенностей исследуемого процесса. В качестве исследуемого сигнала выступает акустическая запись с грудной клетки человека.
Ключевые слова: банк ортогональных фильтров, преобразование Эрмита, функции Эрмита, локальные особенности.
Abstract. The article states the main principles of construction of orthogonal filters bank based on Hermit transform. The test of availability of developed filtering algorithm is realized on the models of pulse sequences based on the sum of Hermit functions. The local features of the investigated process are shown. The acoustic recording with human chest is performed as a test signal.
Keywords: bank of orthogonal filters, Hermit transform, Hermit functions, local features.
Введение
Банком фильтров можно
назвать устройство, которое разбивает входной сигнал на ![]() сигналов, каждый
из которых несет индивидуальную информацию об исследуемом процессе. В основе
разработанного банка фильтров лежит преобразование Эрмита. Преобразование
Эрмита – это полиномиальное
преобразование с производной гауссовой оконной функцией [1]. Преобразование Эрмита находит широкое применение в обработки и
кодирования изображения [2], в областях распознавания и идентификации сигналов [3,4].
Разложение исследуемого процесса на базисные функции Эрмита также применяется в
медицинской диагностике [5]. Несомненным преимуществом разработанного банка
фильтров является возможность поиска локальных особенностей сигнала. Это позволяет определять
значения интервалов следования выбранной характерной особенности процесса, что
может нести важную диагностическую информацию об
исследуемом объекте. Таким образом, разработка банка фильтров на основе преобразований
Эрмита является актуальной задачей.
сигналов, каждый
из которых несет индивидуальную информацию об исследуемом процессе. В основе
разработанного банка фильтров лежит преобразование Эрмита. Преобразование
Эрмита – это полиномиальное
преобразование с производной гауссовой оконной функцией [1]. Преобразование Эрмита находит широкое применение в обработки и
кодирования изображения [2], в областях распознавания и идентификации сигналов [3,4].
Разложение исследуемого процесса на базисные функции Эрмита также применяется в
медицинской диагностике [5]. Несомненным преимуществом разработанного банка
фильтров является возможность поиска локальных особенностей сигнала. Это позволяет определять
значения интервалов следования выбранной характерной особенности процесса, что
может нести важную диагностическую информацию об
исследуемом объекте. Таким образом, разработка банка фильтров на основе преобразований
Эрмита является актуальной задачей.
1. Функции Эрмита
Следуя [1,2,3,4], будем использовать функцию Эрмита (ФЭ), которая в соответствии с [6,7] можно представить в следующей форме:
где ![]() − полиномы
Эрмита.
− полиномы
Эрмита.
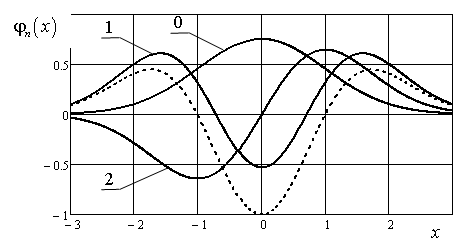
Рис. 1. Функции Эрмита: нулевого – 0, первого – 1 и второго порядка – 2; штриховая кривая – MHAT-функция «мексиканская шляпа»
Функции Эрмита обладают, как пространственной, так и частотной локализацией. Кроме того они образуют ортонормированный базис функций как во временной, так и в частотной области. Это позволяет использовать их в качестве «материнской» функции в вейвлет-преобразовании [8]:
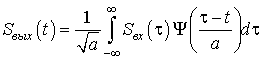 (2)
(2)
где ![]() −
параметр масштаба.
−
параметр масштаба.
Подставив (1) в (2), получим выражение вейвлет-преобразования на базисе функций Эрмита в следующем виде:
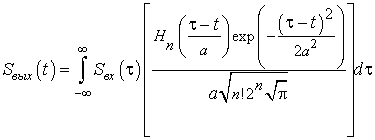 (3)
(3)
Формула (3) представляет собой взаимнокорреляционную
функцию. Принимая во внимание [9], ![]() можно записать в виде преобразования
Фурье:
можно записать в виде преобразования
Фурье:
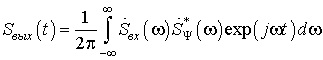 (4)
(4)
где 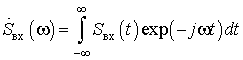 − спектральная плотность входной сигнала,
− спектральная плотность входной сигнала, 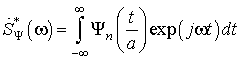 − комплексно
сопряженное преобразование Фурье от функции
− комплексно
сопряженное преобразование Фурье от функции ![]() .
.
В преобразовании (4) произведение перед экспонентой можно рассматривать спектральную плотность сигнала на выходе фильтра:
![]()
комплексный коэффициент передачи которого равен:
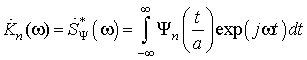 . (5)
. (5)
Подставляя функций вида (1) в (5), находим комплексный коэффициент передачи фильтров:
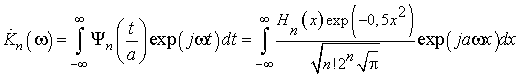
Воспользовавшись [10], получаем комплексный коэффициент передачи фильтра n-го порядка в виде:
Функции (6) образуют ортогональный базис частотных характеристик, т к.
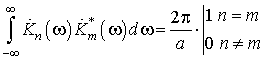 .
.
Спектр сигнала на выходе
фильтра порядка ![]() будет иметь вид:
будет иметь вид:
![]() .
(7)
.
(7)
В выражение (7)
ради удобства записи веден коэффициент 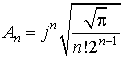 и переменная
и переменная
![]() .
.
Таким образом, использование ортонормированного базиса функций Эрмита в качестве «материнских вейвлетов» эквивалентно фильтрации сигнала с помощью банка ортогональных фильтров.
На практике, вейвлет-преобразование использует разнообразные материнские функции, такие как, например, «Морле», MHAT-функция [11]. На рис.1 видно, что MHAT-функция близка к функции Эрмита второго порядка. По сравнения с традиционными функциями, функции Эрмита позволяют осуществить более точную фильтрацию сигнала определенной формы. Это связано с тем, что широкий класс функций можно представить в виде дискретного ряда, используя преобразование Эрмита [12].
На основании приведенных выше выкладок операцию обработки сигнала можно представить в виде структурной схемы, показанной на рис. 2.
Варьируя параметр масштаба фильтра, можно обнаружить присутствие функции Эрмита заданного порядка в исследуемом сигнале. При совпадение длительности функции Эрмита и параметра масштаба фильтра с параметрами сигнала будем наблюдаться локальные максимумы и минимумы.
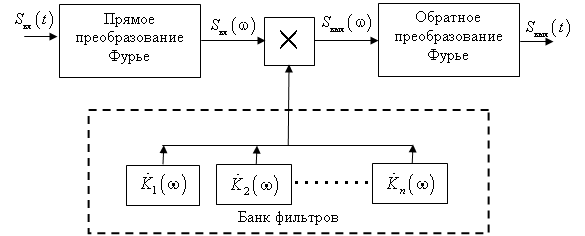
Рис. 2. Структурная схема алгоритма
В качестве демонстрации этого рассмотрим тестовые модели, состоящие из Эрмитов заданного порядка.
2. Тестирование алгоритма
В качестве тестовой модели использовалась периодическая последовательность
импульсов, в виде функций Эрмита второго порядка (см. рис.3). Общая
длительностью тестового сигнала равна 1
с, а период следования импульсов – ![]() с.
с.
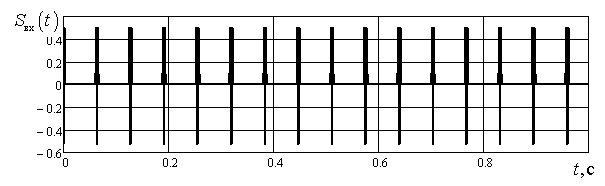
Рис. 3 Тестовый сигнал в виде периодической последовательности функций Эрмита второго порядка
На рис. 4 приведены частотные характеристики фильтров нулевого, второго, четвертого и шестого порядков, рассчитанные по формуле (6).
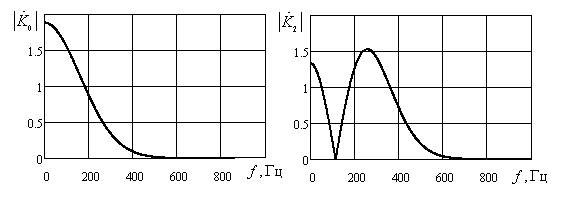
а б
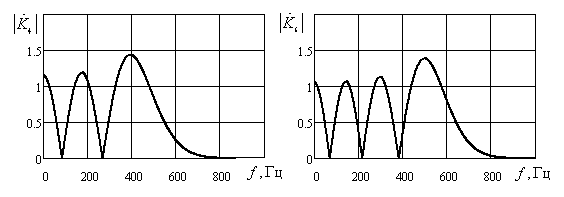
в е
Рис. 4 Амплитудно-частотные характеристики фильтров нулевого (а), второго (б), четвертого (в) и шестого (г) порядков
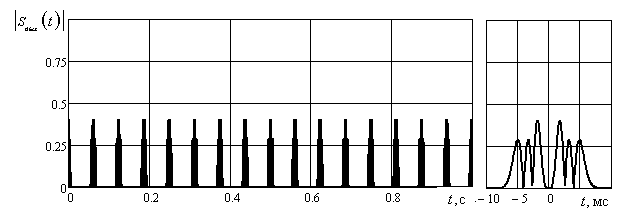
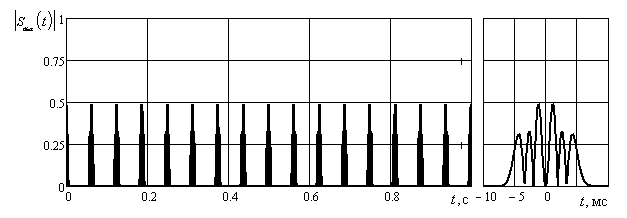
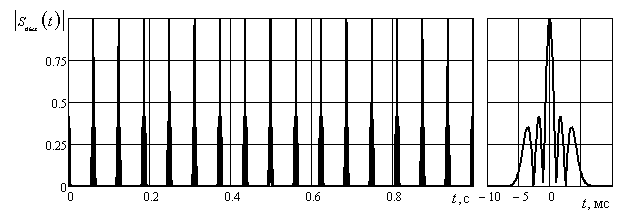
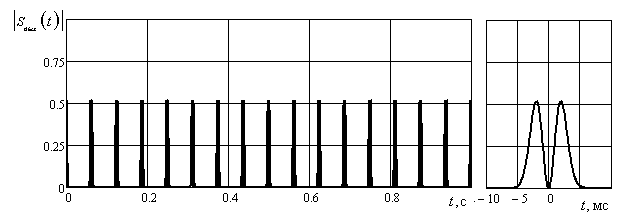
Результаты обработки тестового сигнала представлены на рис. 5. На выходе фильтра второго порядка наблюдается ярко выраженный локальный максимум и боковые лепестки (рис. 5.в), в то время как после обработки сигнала фильтрами нулевого, четверного и шестого (рис. 5.а, ) и г) центральный лепесток отсутствует, а уровень боковых лепестков не превышает величины ≈ 0,5.
а
б
в
г
Рис. 5. Результаты обработки сигнала, показанного на рис. 3 фильтрами:
а – шестого, б – четвертого, в – второго и г – нулевого порядков
Продемонстрируем обработку аддитивной смеси шума и сигнала в виде квазипериодической последовательности импульсов, каждый из которых состоит из разности функций Эрмита нулевого и первого порядков. Форма такого сигнала напоминает запись электрокардиографа (см. рис. 6 справа). Длительность выборки 16 с., среднее значение периода равно 1 с., дисперсия шума ≈ 0,08 В2, шумовая полоса около 200 Гц.
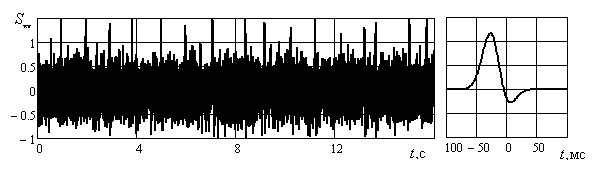
Рис. 6. Имитация сигнала электрокардиографа
Поскольку форма сигнала заранее определена, то функция
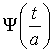 , нормированная к единице, равна:
, нормированная к единице, равна:
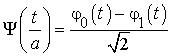
Этой функции соответствует составной фильтр с комплексным коэффициентом передачи:
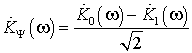
Результат обработки представлен на рис. 7.
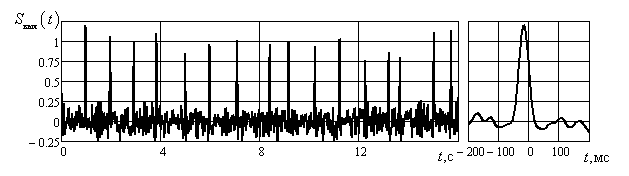
Рис. 7. Результат вейвлет-преобразования на базисе функций Эрмита
3. Пример обработки реального сигнала
В качестве примера, приведем процедуру обработки записи биений сердца на фоне акустических шумов, которая была получена с использованием разработанной нами электронного стетоскопа [13]. Фрагмент записи показан на рис. 8. Длительность записи составляет 17 с, частота дискретизации 8000Гц.
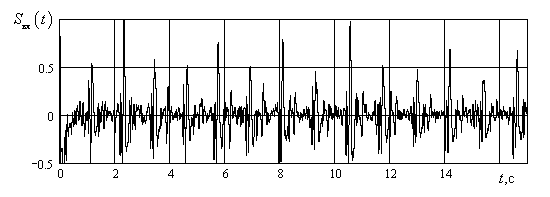
Рис. 8. Запись акустического сигнала с грудной клетки человека
В этом случае достоверных априорных
сведений о форме импульсного сигнала нет. Поскольку наиболее ценная информация
об активности сердца содержится в импульсах, то целесообразно предварительно выделить
один из них и использовать его в качестве образчика полезного сигнала. Выделение
можно выполнить, используя функцию Эрмита нулевого порядка. Численное значение
параметра функции 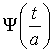 , нужно определить так, чтобы не
потерять характерные детали импульса с одной стороны и не захватить шумы и
помехи, с другой. Ясно, что эта задача не имеет строгого аналитического решения.
Определение границ фрагмента, представляющего интерес, во многом определяется
предыдущим опытом исследователя.
, нужно определить так, чтобы не
потерять характерные детали импульса с одной стороны и не захватить шумы и
помехи, с другой. Ясно, что эта задача не имеет строгого аналитического решения.
Определение границ фрагмента, представляющего интерес, во многом определяется
предыдущим опытом исследователя.
На рис. 9 приведен фрагмент записи
между 2 и 3 секундой. Интервал ![]() с можно принять за
область, где существует импульс биения сердца. Середина интервала находится в
точке
с можно принять за
область, где существует импульс биения сердца. Середина интервала находится в
точке ![]() . Максимум функции Эрмита следует совместить
с этой точкой. Что касается масштаба, то также как в [14] критерий для его определения
выберем так, чтобы
. Максимум функции Эрмита следует совместить
с этой точкой. Что касается масштаба, то также как в [14] критерий для его определения
выберем так, чтобы
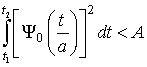
Однако в отличие от [14], примем более
жесткий критерий с![]() , что соответствует
, что соответствует ![]() . Это дает значение параметра
. Это дает значение параметра ![]() . На рис. 9 показан результат локализации
импульса, проведенный изложенным методом.
. На рис. 9 показан результат локализации
импульса, проведенный изложенным методом.
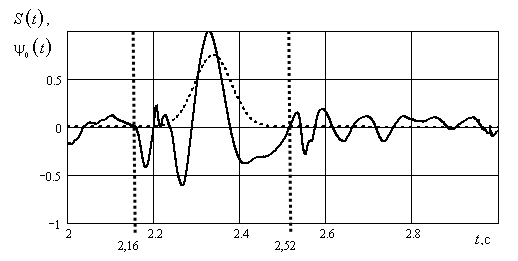
Рис. 9. Локализация фрагмента сигнала (сплошная) с помощь функции Эрмита нулевого порядка (штрих); вертикальные линии – границы импульса
Теперь можно перейти к синтезу образчика сигнала. Для этого представим выделенный фрагмент в виде суммы функций Эрмита [14, 15]. Амплитуды дискретного спектра равны:
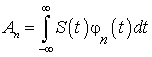 .
.
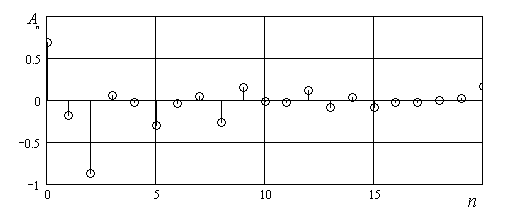
Рис. 10. Спектр фрагмента сигнала на базисе функции Эрмита
Спектр представлен на рис. 10.
Функции Эрмита более высоких порядков соответствуют более быстрым колебанием во
временной области. Видно, что основной вклад в исследуемый импульс дают функции
с номерами не превышающими 10. Если удержать бесконечное число членов ряда, то
импульс будет воспроизводиться полностью (при условии сходимости ряда [15]).
Однако ясно, быстропеременные процессы, прежде всего, связаны с помехами и
шумами (например, с шумами дыхания). Потому вполне оправданным является ограничение
спектра ![]() функциями Эрмита с
функциями Эрмита с ![]() .
Такое ограничение можно рассматривать как фильтрацию в пространстве функций Эрмита.
.
Такое ограничение можно рассматривать как фильтрацию в пространстве функций Эрмита.
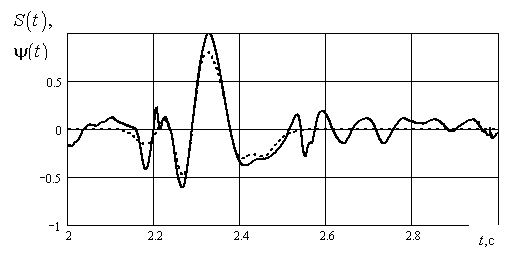
Рис. 11. Сопоставление фрагмента сигнала и вейвлет функции
Нормированная функция образчика сигнала имеет вид:
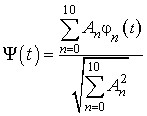 (8)
(8)
На рис. 11 видно, что усеченный ряд (8) хорошо воспроизводит импульс в пределах выделенного интервала и практически полностью подавляет быстрые малые колебания вне интервала.
Используя (6), получаем комплексный коэффициент передачи фильтра, согласованного с образчиком сигнала:
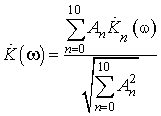 .
(9)
.
(9)
На рис. 12 показаны спектр исходного сигнала и модуль коэффициента передачи согласованного фильтра.
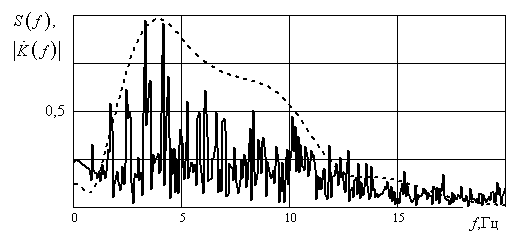
Рис. 12. Сопоставление спектра сигнала и АЧХ фильтра
Результат использования фильтра (9) показан на рис.13. Видно, что быстрые флуктуации подавлены, а максимумы локализованы в точках на оси времени, которые соответствуют моментам появления импульсов. Такую локализацию можно использовать для выявления особенностей сердечного ритма на больших отрезках времени.

Рис. 13. Результат обработки.
Заключение
Для увеличения скорости вычисления коэффициентов передачи фильтров можно воспользоваться свойством рекуррентного соотношения для полиномов Эрмита:
![]() .
.
В результате получаем рекуррентное соотношение для комплексных коэффициентов передачи фильтров:
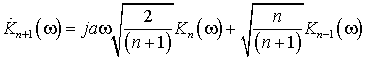
Для обработки изображения в качестве базиса можно использовать двумерное преобразование Эрмита [1, 2]:
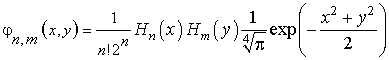
Такое преобразование Эрмита нашло применение, например, для идентификации человека по радужной оболочке глаза [3]. Следует отметить, что при исследовании объектов, обладающих осью симметрии, вместо полиномов Эрмита целесообразно использовать полиномы Лагерра.
Литература
3. Е.А. Павельева, А. С. Крылов. Поиск и анализ ключевых точек радужной оболочки глаза методом преобразования Эрмита. // Информатика и её применения, 2010, т. 4, №. 1, с. 79−82.
4. Е.А. Павельева, А. С. Крылов, О. С. Ушмаев. Развитие информационной технологии идентификации человека по радужной оболочке глаза на основе преобразований Эрмита. // Системы высокой доступности, 2009, №. 1, с. 36−42.
5. Н.В. Мамаев, А. С. Лукин, Д. В. Юрин, М. А. Глазкова, В. Е. Синицин. Алгоритм нелокального среднего на основе разложения по функциям Эрмита в задачах компьютерной томографии. // 23-я международная конференция по компьютерной графике и зрению GrephiCon 2013. Владивосток, Россия, 2013, с. 254−258.
6. Е. Янке, Ф. Эмде, Ф. Лёш. Специальные функции. – М.: Наука, 1964. – 344 с.
7. Г. Сеге. Ортогональные многочлены. – М.: Физматгиз, 1962, – 500 с.
8. Д. А. Балакин, В. В. Штыков. Использование функций параболического цилиндра для вейвлет-анализа. // Вестник МЭИ , 2013, №5, с. 119-123.
9. С. И. Баскаков. Радиотехнические цепи и сигналы. – М.: Высш. школа, 2000, – 450 с.
10. И С Градштейн, И. М. Рыжик Таблицы интегралов, сумм рядов и произведений. – М.: Физматгиз, 1963, – 1100 с
11. Н. М. Астафьева. Вейвлет-анализ: основы теории и примеры применения. // Успехи физических наук, 1996, №11, том 166.
12. П. К. Суетин. Классические ортогональные многочленеы, М.: Физматлит, 2005, – 480 с
13. Д. А. Балакин. Цифровой стетоскоп. //Биомедицинская радиоэлектроника, 2012, №9, с.58-62.
14. Жирков А. О. Нейросетевой анализ и сопоставление частотно - временных векторов на основе краткосрочного спектрального представления и адаптивного преобразования Эрмита. // A.О. Жирков, Д.Н. Корчагин, А.С. Лукин, А.С. Крылов, Ю.М. Баяковский. – М.: Институт прикладной математики РАН, 2001.
15. Математическая энциклопедия т. 5 Под ред. Виноградова И.М. – М.: Советская энциклопедия, 1985, – 623 с.