Эффекты полузатенения на изображении, сформированным объективом с большой апертурой

Эффекты полузатенения на изображении, сформированном объективом с большой апертурой

А. Ю. Зражевский, В. А. Коротков, К. В. Коротков
ИРЭ им. В.А.Котельникова РАН, Фрязинский филиал

Статья получена 18 сентября 2014 г.

Аннотация. В данной работе, в рамках геометрической оптики рассмотрено проявление на изображении эффектов полузатенений объектов друг другом. Предполагается, что величина апертуры объектива больше одного из размеров затеняющего объекта. Показана возможность восстановления расфокусированного изображения объекта, затененного другим объектом, с помощью метода опорного изображения.

Ключевые слова: радиовидение, миллиметровый диапазон волн, дефокусированное изображение.

Abstract: In this paper, in the framework of geometrical optics a manifestation of the image effects of semidarkness of objects by each other is considered. It is assumed that the size of the aperture of the lens more than one size of the shading object. The possibility of recovery of-focus image of an object, shaded by another object using method of the basic image.

Key words: radio vision, millimetric wave band, defocused image.

Сравнение формирования изображений в миллиметровом диапазоне длин волн (ММВ) с оптическим диапазоном показывает, что апертуры объективов, используемых в этих диапазонах существенно отличаются. Это вызвано соотношением длин волн в этих диапазонах. В ММВ апертуры объективов имеют размер десятки сантиметров и более, что делает их сравнимыми с размерами объектов (люди, растения, техника …). Если объекты, изображения которых получают, расположены так, что частично затеняют друг друга, то вид изображения существенным образом зависит от того, как сфокусирована формирующая изображение оптическая система.

Формирование изображений 2 объектов.

На Рис.1 представлена схема оптической системы с двумя объектами.

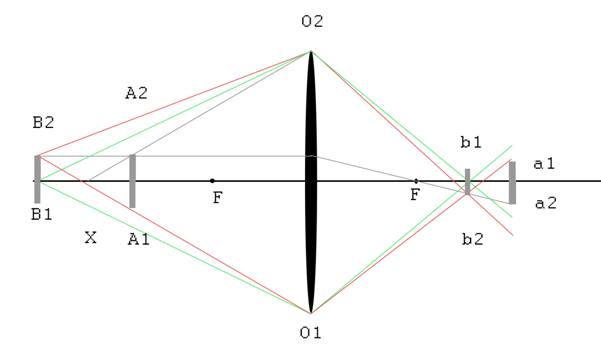
Рис.1. Схема оптической системы. O1-O2 – объектив; F – фокус; A1-A2 и B1-B2 – объекты
a1-a2 и b1-b2 – изображения объектов; серые, красные и зеленые линии показывают ход лучей, формирующих изображения;
X – расстояние, на котором возможно полное затенение дальнего объекта объектом A1-A2.

Если смотреть на объект B1-B2 из центра объектива, то B1-B2 полностью затеняется объектом A1-A2. С края объектива при представленном расположении объектов объект B1-B2 виден полностью. Красные и зеленые линии соответствуют лучам, участвующим в формировании верхнего края и центра изображения объекта B1-B2 соответственно. Видно, что лучи, участвующие в формировании изображения b1-b2, формируют своеобразный ореол вокруг изображения a1-a2. Этот ореол представляет собой расфокусированное изображение b1-b2.

Для исследования явления полузатенения была создана программа, которая основана на геометрической оптике. Весь объект представлен как набор блестящих точек – пикселов. Из каждой точки исходят лучи, которые распространяются прямолинейно. Если на пути этих лучей к объективу не встает другой объект (который предполагается непрозрачным), то лучи достигают объектива. Объектив имел форму круга и был вписан в квадрат, разделенный на частей. Каждая часть объектива изменяла направление распространения падающего на нее луча так, чтобы в дальнейшем этот луч пересек соответствующую точку на плоскости изображения данного объекта. Эта плоскость расположена на расстоянии от объектива, соответствующем основной формуле линзы [1]:

, (1)

где соответствуют фокусному расстоянию, расстояниям от объектива до объекта и от объектива до изображения.

Если расположить плоскость изображения на другом расстоянии, отличном от , то лучи, исходящие из точки объекта пересекут эту плоскость не в одной точке, а в некоторой области (область дефокусировки). Размер этой области можно оценить исходя из Рис.1 как:

, (2)

где - апертура объектива, - размер области дефокусировки, - расстояние от объектива до области дефокусированного изображения. Форма области дефокусировки в случае круглого объектива и в отсутствии затеняющего объекта имеет форму эллипса. Затеняющий объект изменяет форму этой области на более сложную.

Из Рис.1 следует, что если плоскость получаемого изображения расположить на месте формирования изображения b1-b2, то на ней будет присутствовать расфокусированное изображение объекта A1-A2 и сфокусированное изображение объекта B1-B2 одновременно, частично перекрывая друг друга. Следует отметить, что вследствие частичного затенения изображение b1-b2 имеет искаженное по сравнению с объектом B1-B2 распределение яркости.

Если плоскость получаемого изображения расположить на месте формирования изображения a1-a2, то изображение объекта A1-A2 будет сфокусировано. Расфокусированное изображение объекта B1-B2 расположится вокруг сфокусированного изображения объекта A1-A2 и, в отличие от предыдущего случая, взаимного перекрытия изображений не будет.

На Рис.2 представлены фотографии тестовых объектов, изображения которых рассчитывались с помощью выше указанной программы.

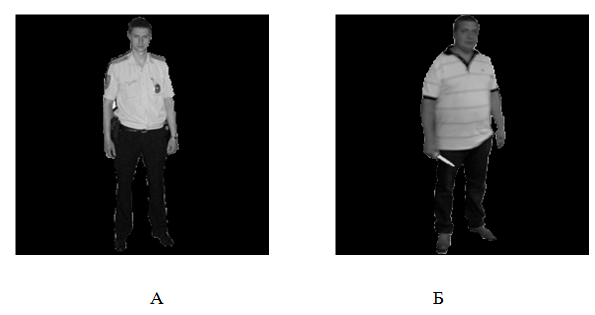
Рис.2. Объекты, используемые для расчетов изображения. Объект A1-A2 соответствует А, объект B1-B2 – Б.

Объекты, представленные на рис.2 имеют размер 1.7м по высоте и рассчитывались как состоящие из 256х256 пикселей. Черный фон, на котором расположены объекты, считался прозрачным (незатеняющим). Объекты располагались от объектива на расстояниях . Апертура и фокусное расстояние объектива и . Сфокусированные изображения объектов располагаются соответственно на и . Результаты расчетов представлены на Рис.3-4.

Рис.3. Изображение, полученное на плоскости, расположенной на от объектива.
Изображение, соответствующее объекту B1-B2 – А, объектам A1-A2 и B1-B2 вместе –Б.
Зеленый цвет соответствует изображению объекта B1-B2, а фиолетовый - изображению объекта A1-A2. Размер изображения - 0.85м.

Рис.4. Изображение, полученное на плоскости, расположенной на от объектива.
Изображение, соответствующее объекту B1-B2 – А, объектам A1-A2 и B1-B2 вместе –Б.
Зеленый цвет соответствует изображению объекта B1-B2, а фиолетовый - изображению объекта A1-A2. Размер изображения - 1.7м.

Сравнение Рис.2Б и Рис.3А позволяет сделать вывод о том, что вследствие влияния затенения объектом A1-A2 происходит искажение поля яркости изображения объекта B1-B2. На Рис.3Б видно, что при таком расположении плоскости получения изображения происходит наложение изображений объектов A1-A2 и B1-B2 друг на друга.

Изображение Рис.3А при изменении положения плоскости получения изображения с на переходит в Рис.4А. Понятно, что расфокусированное изображение объекта B1-B2 на Рис.4А содержит ту же информацию, что и изображение на Рис.3А. Это позволяет надеяться, что из Рис.4А можно получить Рис.3А. Изображение совокупности объектов A1-A2 и B1-B2 представлено на Рис.4Б. На Рис.4Б хорошо видно, что области, соответствующие разным объектам и показанные разными цветами не перекрываются и располагаются рядом.

Восстановление изображения затененного объекта

В работе [2] для решения задачи восстановления изображения нескольких объектов, в разной степени расфокусированных, был использован способ разбиения исходного большого изображения на отдельные спрайты с последующей их обработкой. Однако, в рассматриваемом случае этот подход бесперспективен. Одним из возможных решений этой задачи может быть предварительная обработка исходного изображения с выделением области, занятой затеняющим изображением, заменой яркостной информации в этой области и применением спектрального метода для восстановления затененного изображения. Такой подход обусловлен тем, что в рассматриваемом случае наличия затенений расчет изображения с помощью свертки неприменим. Следовательно, и восстановление, основанное на уравнении свертки некорректно. Рассмотрим это на примере объектов – Рис.2.

В данной части для упрощения анализа результатов мы будем вместо затеняющего предмета использовать черный прямоугольник - Рис.5Б.

На Рис.5А приведено расфокусированное изображение объекта Рис.2Б, (затеняющий объект – Рис.2А). На Рис.5Б – расфокусированное изображение объекта Рис.2Б, рассчитанное с помощью свертки с аппаратной функцией Баттерворта [2] при (затеняющий объект – черный прямоугольник с шириной 88 пикселей). Ширина затеняющего прямоугольника соответствует максимальной ширине затеняющего объекта Рис.2А.

Рис.5. Изображение, полученное на плоскости, расположенной на от объектива
и соответствующее объекту B1-B2, затененному объектом Рис.2А – А.
Изображение рассчитанное с помощью свертки и затененное черным прямоугольником шириной 88 пикселей – Б.

Использование выражения свертки для расчетов расфокусированного объекта в области сфокусированного изображения затеняющего объекта при условии последующего наложения этого объекта вполне корректно. Однако при восстановлении расфокусированного изображения возникают трудности, описанные в работе [2]. В отличие от [2] в данной работе рассматривается восстановление расфокусированного изображения затененного объекта. Применим операцию деконволюции с использованием метода опорного изображения (МОИ) [3] к Рис.5Б. Полученный результат представлен на Рис.6А. Для сравнения на Рис.6Б представлен результат восстановления из Рис.5А, где в качестве затеняющего объекта используется Рис.2А.

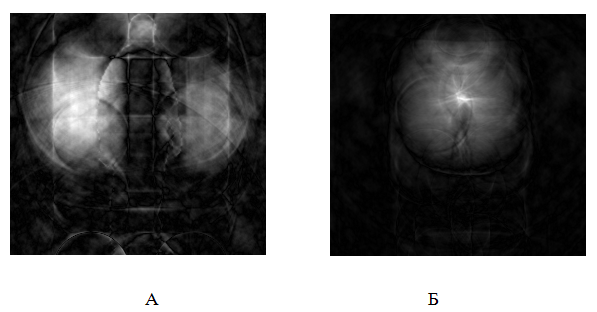
Рис.6. Изображение, восстановленное с помощью МОИ из Рис.5Б – А.

Изображение, восстановленное с помощью МОИ из Рис.5А – Б.

Результат, представленный на Рис.6Б, аналогичен результатам восстановления нескольких в разной степени расфокусированных изображений и был разобран в [2] и поэтому не вызывает вопросов. Неудачный результат, который был получен восстановлением только одного расфокусированного изображения – Рис.5Б объясняется наличием затеняющего черного прямоугольника на месте части расфокусированного изображения. Если описать формирование расфокусированного затененного изображения в виде соответствующей системы линейных уравнений, то решение этой системы позволит решить задачу восстановления. Однако, несмотря на то, что основная матрица этой системы имеет вид ленточной матрицы, решение этой системы отнюдь не тривиальная задача из-за большого количества уравнений. В то же время, если использовать в качестве описания задачи уравнение свертки, решение задачи может проводиться на основе известного метода опорного изображения [3]. Препятствием для такого решения является наличие затеняющего объекта.

Расфокусированное изображение в силу того, что объектив выступает как фильтр низких частот, имеет вид сглаженный, с отсутствием мелких деталей изображения. Эта особенность позволяет заменить отсутствующую часть расфокусированного изображения, затененного другим объектом, на изображение, полученное например с помощью интерполяции неизвестной части изображения. В данной работе мы будем использовать линейную интерполяцию.

На Рис.7 представлены результаты восстановления расфокусированного изображения в зависимости от ширины затеняющего черного прямоугольника.

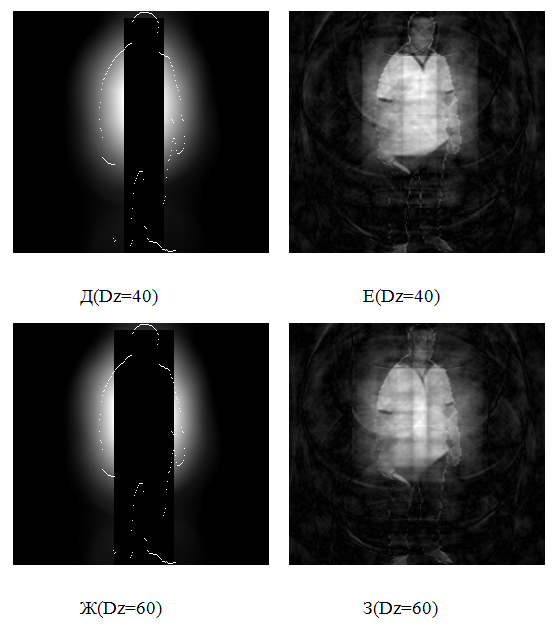
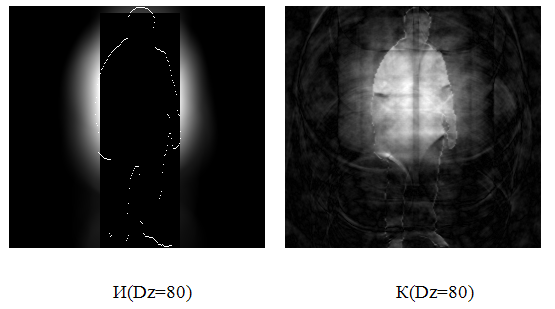
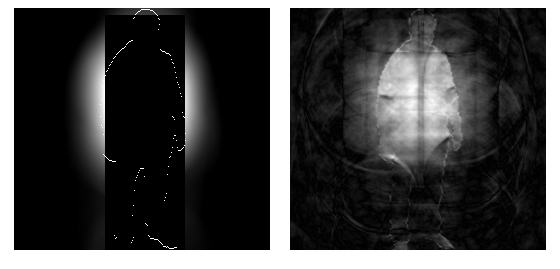
Л(Dz=100) М(Dz=100)

Рис.7. Изображения, расфокусированные с помощью аппаратной функции Баттерворта [2] при ,
затененные черным прямоугольником с шириной Dz и восстановленные с помощью МОИ [3] (при условии линейной интерполяции).
Для наглядности величины затеняющего прямоугольника на изображение нанесен контур расфокусированного затененного объекта.

Рис.7 достаточно наглядно иллюстрирует следующие закономерности:

- с увеличением ширины затеняющего прямоугольника теряется часть яркостной информации о расфокусированном изображении;

- потеря яркостной информации влечет за собой появление артефактов на восстановленном изображении;

- артефакты располагаются на всем восстановленном изображении, а не только на той части, которая соответствует затенению;

- необратимая потеря яркостной информации проявляется внутри затеняющего прямоугольника и находится на расстоянии от его периметра.

Авторы выражают благодарность Самохину И.С. за предоставленные материалы и ценные советы.

Выводы:

1.Вид изображения совокупности объектов, расположенных на разном расстоянии от объектива и частично затеняющие друг друга, сильно зависит от расположения плоскости получения изображения.

2.Расположение плоскости получения изображения в месте фокусировки изображения ближнего объекта позволяет получить изображение (сфокусированное ближнего объекта и расфокусированное дальнего объекта) в виде неперекрывающихся областей.

3. Расположение плоскости получения изображения в месте фокусировки изображения затененного объекта позволяет получить сфокусированное изображение этого объекта. Это изображение будет иметь искажение поля яркости изображения объекта вследствие эффекта частичного затенения.

4. В работе показана возможность восстановления расфокусированного изображения частично затененного объекта.

5. Несмотря на то, что интересующий объект может быть затенен объектом большего размера, восстановление расфокусированного изображения возможно.

6. Невосстановимая область определяется размером затеняющего объекта и величиной расфокусировки изображения интересующего объекта.

7. Восстановление возможно производить с помощью метода опорного изображения (МОИ).

8. При использовании МОИ для восстановления расфокусированного изображения затененного объекта необходима предварительная обработка этого изображения с помощью метода интерполяции.

Литература

1. В.А.Зверев. Радиооптика. М. «Советское радио». 1975 г.

2. А. Ю. Зражевский, В. А. Коротков, К.В. Коротков. Типичные проблемы восстановления изображений: дефокусировка и смазанное изображение. Результаты применения метода опорного изображения. «Журнал Радиоэлектроники» [электронный журнал]. 2014. №4. URL: http://jre.cplire.ru/jre/apr14/11/text.html

3. Ю. В. Гуляев, А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков, В. А. Черепенин. Коррекция пространственного спектра, искаженного оптической системой, с помощью метода опорного изображения.
Часть 2. Адаптивный метод опорного изображения (АМОИ). // Журнал Радиоэлектроники [электронный журнал]. 2013. №12. URL: http://jre.cplire.ru/jre/dec13/2/text.html