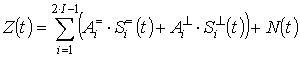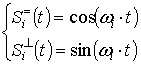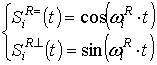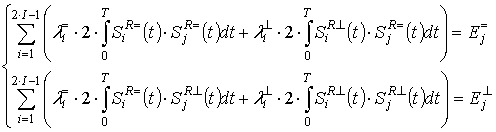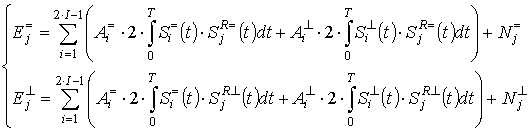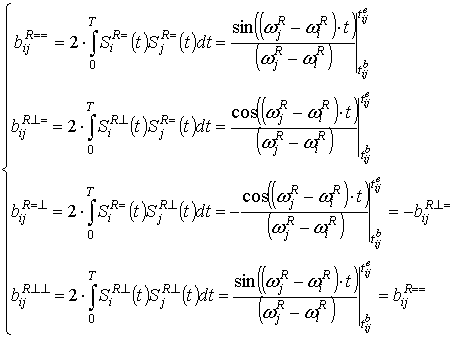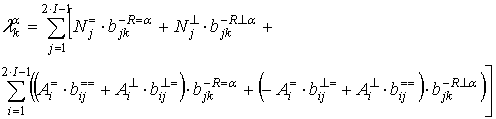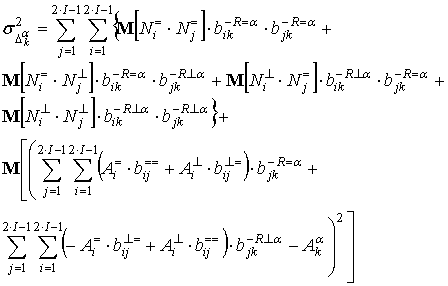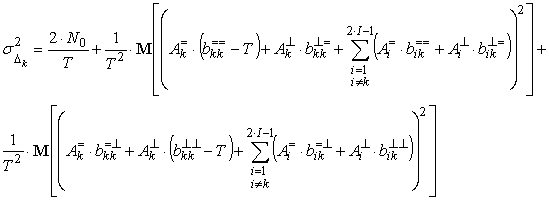УДК 621.396.49

ОЦЕНКА ЭФФЕКТИВНОСТИ ПРИМЕНЕНИЯ АЛГОРИТМА ОПТИМАЛЬНОГО ИЗМЕРЕНИЯ ПАРАМЕТРОВ OFDM СИГНАЛОВ

 

Е. А. Спирина

Казанский национальный исследовательский технический университет им. А.Н. Туполева

 

Статья поступила в редакцию 22 июня 2016 г., после доработки – 8 сентября 2016 г.

 

Аннотация. Статья посвящена анализу отклонений оценок параметров канальных сигналов OFDM систем при асинхронной работе оборудования на различных частотных каналах для двух алгоритмов демодуляции: стандартного на основе БПФ и алгоритма оптимального измерения по критерию максимума правдоподобия. В работе выводятся выражения для оценки отклонений измеренных параметров сигналов от их истинных значений для общего случая, а также подробно рассматривается передача сигналов на двух поднесущих с известными частотами и временами задержек. Для последнего случая проводится сравнительная оценка зависимости дисперсий отклонений от параметров сигналов и вида используемого алгоритма, показавшая, что оба алгоритма приёма обеспечивают несмещённую оценку квадратурных компонент сигнала на первой поднесущей. При этом дисперсии оценок алгоритмов приёма кроме мощности белого гауссовского шума на первой поднесущей включают для стандартного алгоритма приёма мощность внутрисистемных помех от сигналов, передаваемых на второй поднесущей, а для алгоритма оптимального измерения мощность белого гауссовского шума на второй поднесущей. Указанное отличие позволяет сделать предположение о преимуществе применения алгоритма оптимального измерения при больших отношениях сигнал/шум, характерных для сетей широкополосного радиодоступа.

Ключевые слова: OFDM, БПФ, демодуляция, оптимальное измерение, критерий максимума правдоподобия.

Abstract. This article presents the analysis of parameters estimations for the OFDM channel signals under asynchronous operation of the equipment on various frequency channels for two demodulation algorithms: standard FFT algorithm and optimal measuring by maximum likelihood estimation algorithm. It contains expressions for deviation estimations of the measured signal parameters of their true values for the general case. Also it considers detail analysis of transmitting signals on two subcarriers with known frequency and time delay. For the latter case, paper presents a comparison of the deviation dispersions to depend on the signal parameters and the type of algorithm used, which showed that both algorithms provide unbiased estimates of the receiving signal quadrature components at the first subcarrier. Thus on receiving the first subcarrier variance estimates algorithms except white Gaussian noise include standard algorithm for receiving intra-system interference power from signals transmitted on the second subcarrier, and the algorithm for optimal measurement white Gaussian noise on the second subcarrier. This difference leads to the assumption that the benefits of applying the optimal measurement algorithm at high S/N ratio characteristic of broadband wireless access networks.

Key words: OFDM, FFT, demodulation, optimal measurement, maximum likelihood estimation.

 

Введение

В сетях широкополосного радиодоступа в связи с асинхронным режимом работы передающих устройств на интервале демодуляции OFDM сигнала могут присутствовать сигналы, соответствующие двум соседним кодовым символам, что приводит к возникновению внутрисистемных помех.

Модель описания реальной сигнально-помеховой обстановки OFDM систем, учитывающая указанную возможность, предложена в работе [1]. Эта модель позволяет определить отношение сигнал/помеха для каждой поднесущей OFDM сигнала на основе мощностей сигнала полезной и мешающих базовых станций для фиксированных сетей широкополосного радиодоступа. Однако предложенная модель разработана для стандартного алгоритма приёма, что не позволяет провести анализ эффективности использования различных алгоритмов приёма в рассматриваемых сетях.

Одним из путей снижения влияния внутрисистемных помех, а значит повышения эффективности этих сетей, является использование альтернативных алгоритмов приёма, базирующихся на задачах разрешения и измерения параметров сигналов [2-4]. Следовательно, актуальным является анализ эффективности использования алгоритмов приёма, базирующихся на этих задачах.

В сетях широкополосного радиодоступа для передачи информации используется большое количество поднесущих. Поэтому применение алгоритма оптимального разрешения сигналов приводит к высокой сложности его реализации. В этом случае актуальным является использование алгоритма оптимального измерения для оценки параметров сигналов на каждой из поднесущих с последующим их независимым декодированием.

Однако применение алгоритма оптимального измерения в сетях широкополосного радиодоступа увеличивает полосу анализируемого сигнала и, соответственно, мощность шума на его входе. Этот факт требует проведения сравнительного анализа отклонений оценок параметров сигналов стандартного алгоритма приёма, базирующегося на быстром преобразовании Фурье (БПФ), и алгоритма оптимального измерения.

При проведении сравнительного анализа указанных алгоритмов наиболее интересным представляется получить зависимости влияния конкретных параметров передаваемых сигналов на дисперсии получаемых оценок.

1. Постановка задачи

Рассмотрим асинхронный режим работы передающих устройств. В этом случае в точке приёма на  различных частотах могут присутствовать сигналы, представленные на (рис.1).

 

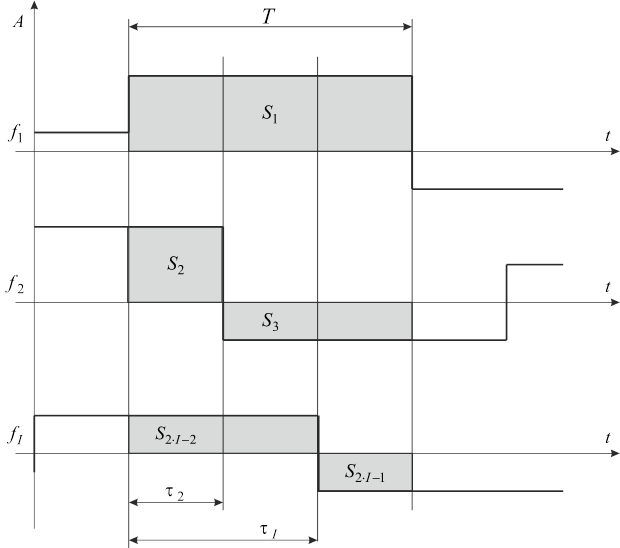
Рис.1. Зависимость сигналов сетей широкополосного радиодоступа от времени

Пусть в системе осуществляется приём сигнала  с частотой  текущего кодового символа на интервале анализа . При этом в точке приёма на частоте  присутствует сигнал  предыдущего кодового символа на интервале  и сигнал  текущего кодового символа на интервале . Аналогично на частоте  существует сигнал  предыдущего кодового символа на интервале  и сигнал  текущего кодового символа на интервале . Коэффициенты  в идеальном случае равняются числу поднесущих, укладывающихся между частотами  и . Для реальных сетей связи значения  могут незначительно отличаться от целых чисел за счёт влияния дестабилизирующих факторов.

В связи с использованием в сетях широкополосного радиодоступа квадратурных способов модуляции, обозначим за  и  квадратурные компоненты опорных сигналов  и  в точке приёма. Тогда сигнал на входе приёмного устройства на интервале анализа  может быть записан:

,                                               (1)

где  – реализация белого гауссовского шума.

Для OFDM систем опорные сигналы представляют собой гармонические колебания с циклическими частотами :

.                                                                               (2)

С учётом (2) выражение (1) примет вид:

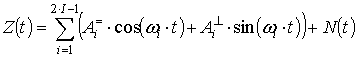.                                    (3)

Рассмотрим задачу оптимального измерения параметров сигналов. В этом случае правило определения оптимальных оценок квадратурных компонент опорных сигналов  и  по критерию минимума среднеквадратического отклонения сводится к нахождению минимума следующего выражения:

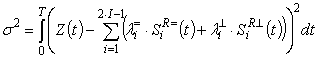,                                            (4)

где  и  – опорные сигналы приёмника с циклическими частотами :

.                                                                            (5)

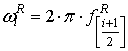Решение задачи (4) для  сводится к решению системы линейных уравнений вида:

,             (6)

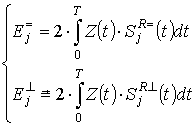где .                                                                       (7)

С учётом выражений (1) и (7) энергии  и  могут быть определены следующим образом:

, (8)

где .

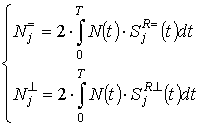Для опорных сигналов приёмника согласно выражению (5) интегралы, входящие в формулу (6), для  определяются как:

,                (9)

где  – время начала, а  – время конца интервала совместного существования -го и -го сигналов.

Аналогичные интегралы для  вычисляются по следующим формулам:

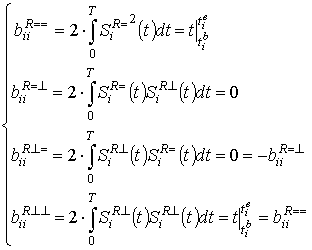,                                             (10)

где  и  – времена начала и конца -го сигнала.

Для определения интегралов, входящих в формулу (8), используем опорные сигналы согласно выражениям (2) и (5):

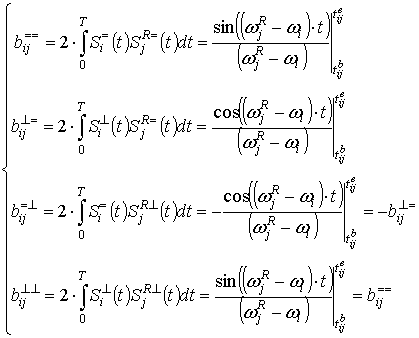.                       (11)

Тогда с учётом выражений (9) – (11) система (6) будет иметь вид:

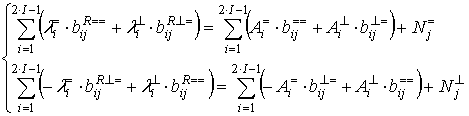.             (12)

Обозначим буквами  и  вид компоненты ( или ), а за  и  – квадратные матрицы размерностью , составленные из коэффициентов  и , соответственно, а за  – матрицу, обратную , с коэффициентами .

Тогда значения оценок квадратурных компонент -го сигнала , где , будут определяться из системы (12) как:

.        (13)

Под точностью оценивания параметров -го сигнала будем понимать отклонения оценок принятых квадратурных компонент от их истинных значений в точке приёма:

.                                                                                      (14)

С учётом выражения (13)  определяются как:

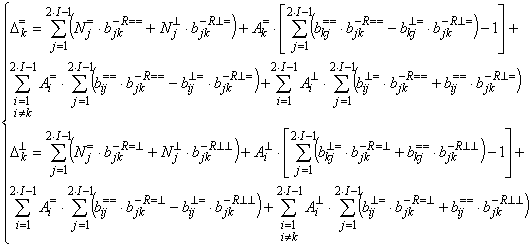. (15)

Так как математическое ожидание белого гауссовского шума и квадратурных компонент сигнала  при равновероятном распределении передаваемых кодовых символов равняются нулю, то из выражения (15) следует, что отклонения оценок имеют нулевые математические ожидания, а их дисперсии  вследствие некоррелированности белого гауссовского шума определяются как:

,              (16)

где  – операция взятия математического ожидания.

Для нахождения дисперсий по формуле (16) необходимо определить математические ожидания вида . Принцип их определения рассмотрим на примере  и .

Значения  и  определяются согласно следующим выражениям:

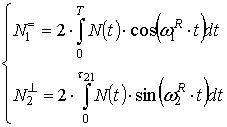.                                                              (17)

В этом случае искомые математические ожидания определяются:

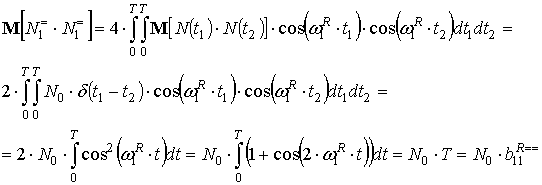, (18)

 

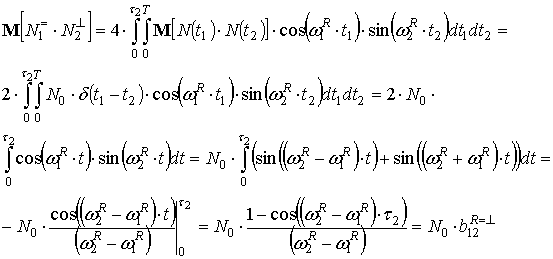, (19)

где  – односторонняя спектральная плотность мощности белого гауссовского шума.

Аналогично можно показать, что . Следовательно, выражение (16) для дисперсии отклонения имеет вид:

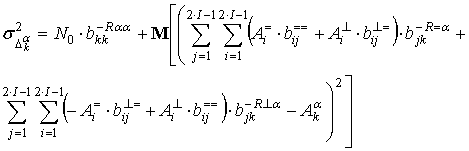.             (20)

Для сравнительной оценки эффективности алгоритмов приёма будем использовать  - дисперсию расстояния между принятыми квадратурными компонентами (, ) и их истинными значениями (, ) для -го сигнала:

                                                                                 (21)

 

2. Стандартный алгоритм приёма

В существующих OFDM системах измерение параметров сигналов, передаваемых на поднесущих, осуществляется с использование алгоритма БПФ. Однако с целью получения единообразного представления результатов оно может быть получено из выражения (13), при задании , для всех .

Действительно, в этом случае коэффициенты  на основе выражений (9) и (10) определяются как:

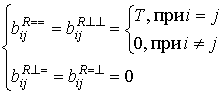.                                                               (22)

Тогда значения оценок  и  определяются следующим образом:

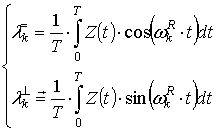, .                                            (23)

Выражение (23) соответствует преобразованию Фурье, реализацией которого в дискретном времени является алгоритм БПФ.

Следовательно, для определения отклонений оценок стандартного алгоритма приёма воспользуемся выражениями (13) и (14) с коэффициентами  согласно выражению (22).

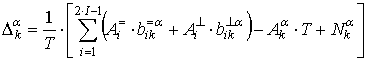,.               (24)

 

Дисперсия  для стандартного алгоритма приёма, согласно выражению (21), определяется следующим образом:

. (25)

3. Алгоритм оптимального измерения

Рассмотрим случай априорной известности параметров сигнала. Тогда  для  и . Тогда значения  на основе выражений (13) и (14) определяются как:

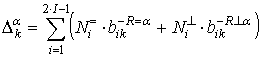.                                                       (26)

Дисперсия  в этом случае, согласно выражению (21), определяется как:

.                                                                     (27)

 

4. Случай наличия сигналов на двух частотах

Для определения параметров сигнала, передаваемого по каждой из поднесущих, используются одинаковые алгоритмы приёма. Поэтому, первоначально, рассмотрим взаимное влияние сигналов на двух частотах. При этом стандартный алгоритм приёма будет корректно оценивать параметры только сигнала на частоте . Поэтому сравнение отклонения оценок будем рассматривать только для него, а сигналы на частоте  будем считать источником внутрисистемных помех.

В этом случае отклонения оценок квадратурных компонент сигнала на частоте  для стандартного алгоритма приёма примут вид:

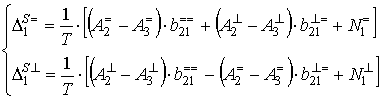,                               (28)

где 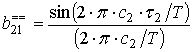, а .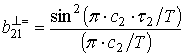

Тогда, согласно выражению (25) дисперсия  для сигнала на частоте  с учётом некоррелированности изменений квадратурных компонент сигналов примет вид:

,                          (29)

где

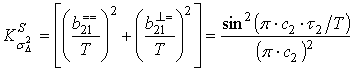.                                    (30)

Согласно формуле (29) дисперсия  содержит две составляющие: мощность белого гауссовского шума в полосе первого канала на частоте  и мощность внутрисистемных помех, зависящая от изменения сигналов, присутствующих на частоте  с коэффициентом .

Коэффициент  зависит от разноса частот  и относительного времени задержки . При задержке кратной длительности интервала анализа  для любого изменения сигналов на частоте , а также при отсутствии изменения сигналов на частоте  для любого времени задержки, вторая составляющая дисперсии  будет равна нулю, что соответствует теории.

Семейство графиков для коэффициента  при значениях , характерных для сетей стандарта 802.11n, приведено на рисунке 2.

 

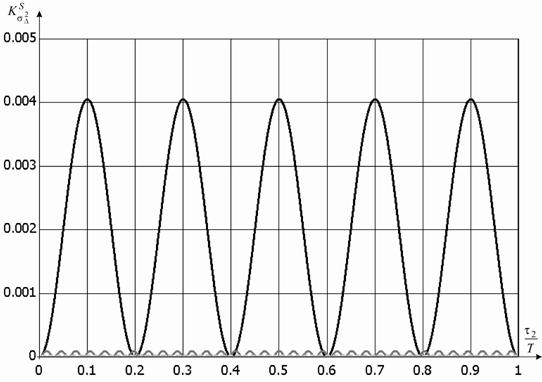
Рисунок 2. Графики зависимости коэффициента  от относительной задержки для :

5 – чёрный; 32 – тёмно серый; 64 – светло серый.

Значение =5 возникает для ближайших поднесущих, а  32 и 64 для поднесущих, разнесённых на половину и полную ширину спектра, двух OFDM сигналов указанного стандарта, предаваемых по соседним частотным каналам.

Отклонения оценок квадратурных компонент сигнала на частоте  для алгоритма оптимального измерения согласно выражению (25) имеют следующий вид:

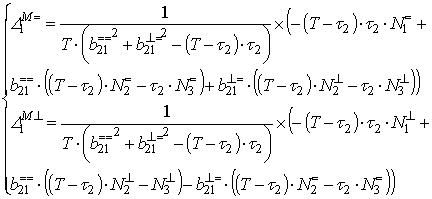.                     (31)

В этом случае дисперсия  для сигнала на частоте  определяется на основе выражения (27) как:

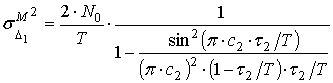.                                         (32)

Выделим из  дисперсию, порождённую мощностью белого гауссовского шума в полосе канала на частоте :

,                                                                (33)

где

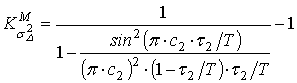.                                                (34)

Согласно формуле (33) дисперсия  также содержит две составляющие: мощность белого гауссовского шума в полосе канала на частоте  и мощность белого гауссовского шума в полосе канала на частоте  с коэффициентом .

Коэффициент  также зависит от разноса частот  и относительного времени задержки . При задержке кратной длительности интервала анализа  вторая составляющая дисперсии  также будет равна нулю, что соответствует теории.

Семейство графиков для коэффициента  при различных  приведено на рисунке 3.

 

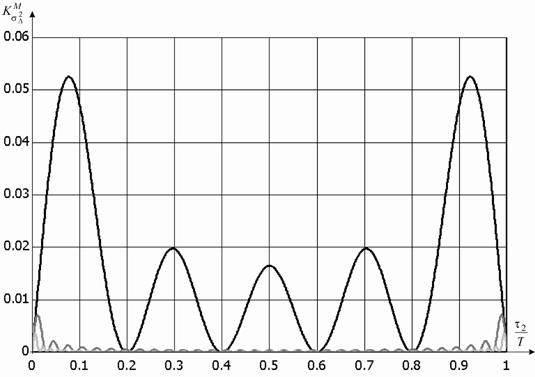
Рисунок 3. Графики зависимости коэффициента  от относительной задержки для :

5 – чёрный; 32 – тёмно серый; 64 – светло серый.

Из графиков видно:

- значения коэффициента  существенно больше значений коэффициента ;

- значения коэффициента  возрастают к краям анализируемого интервала вследствие увеличения погрешности оценки параметров сигналов на частоте  при малой длительности одного из сигналов.

 

5. Выводы

Для рассмотренного в работе случая присутствия сигналов на двух известных частотах с известными временами прихода можно сделать следующие выводы:

1. Стандартный алгоритм приёма обеспечивает несмещённую оценку квадратурных компонент сигнала на частоте . Дисперсия оценки включает кроме мощности белого гауссовского шума в полосе канала на частоте  мощность внутрисистемных помех от сигналов на частоте  с коэффициентом .

2. Алгоритм оптимального измерения также обеспечивает несмещённую оценку квадратурных компонент сигнала на частоте . Дисперсия оценки включает кроме мощности белого гауссовского шума в полосе канала на частоте  и мощность белого гауссовского шума в полосе канала на частоте  с коэффициентом .

Так как для эффективного использования сетей широкополосного радиодоступа требуется большое отношение сигнал/шум, то на основе приведённых результатов можно предположить, что дисперсия стандартного алгоритма приёма, связанная с влиянием сигналов на частоте , будет больше чем дисперсия алгоритма оптимального измерения, обусловленная влиянием шума в полосе канала на частоте .

Однако для окончательного решения вопроса об эффективности применения алгоритма оптимального измерения в реальных OFDM системах необходимо провести дополнительные исследования, направленные на снятие технически нереализуемых ограничений, расширение количества взаимодействующих сигналов и определение их статистических характеристик.

 

Литература

1. Петрова Е.А. Оценка гарантированной информационной скорости передачи в сетях широкополосного радиодоступа с учетом внутрисистемных помех // Журнал радиоэлектроники [электронный журнал]. 2014. №10. URL: http://jre.cplire.ru/jre/oct14/7/text.html.

2. Файзуллин Р.Р., Кадушкин В.В., Воробьев М.С. Файзуллин, Р. Р. Cинтез полигауссовых квазиоптимальных алгоритмов многопользовательской обработки сигналов в комплексе внутрисистемных негауссовских помех // Известия высших учебных заведений. Авиационная техника. 2015. № 3. С. 93-98.

3. Козлов С.В. Новые смесевые подходы к проектированию радиоинтерфейса систем связи. Казань: ООО «Новое знание», 2014. 132 с.

4. Козлов С.В., Чабдаров Ш.М. Квазиоптимальный алгоритм приема сигналов широкополосных систем связи на базе мультимарково-полигауссовых вероятностных моделей // Журнал радиоэлектроники. 2014. № 4. URL: http://jre.cplire.ru/jre/apr14/10/text.html.