Обнаружение периодичности в случайном потоке в условиях априорной неопределенности

УДК 621.37+621.391:519.218.5

ОБНАРУЖЕНИЕ ПЕРИОДИЧНОСТИ В СЛУЧАЙНОМ ПОТОКЕ В УСЛОВИЯХ АПРИОРНОЙ НЕОПРЕДЕЛЕННОСТИ

Ф. В. Голик

Новгородский государственный университет им. Ярослава Мудрого

Статья поступила в редакцию 17 сентября 2016 г.

Аннотация. Статья посвящена разработке метода обнаружения периодической составляющей в случайном потоке в условиях априорной неопределенности относительно параметров потока и при невозможности многократного наблюдения реализаций потока. Доступная для наблюдения реализация потока представляет собой суперпозицию децимированного периодического потока с вобуляцией периода и потока Пуассона.

С целью усиления периодической составляющей потока предложен подход, состоящий в преобразовании потока точек в поток дельта-функций. Амплитудный спектр преобразованного потока является спектральной функцией (СФ) исходного потока.

Показано, что плотность распределения вероятности глобального максимума СФ потока Пуассона хорошо аппроксимируется альфа-распределением. Методом статистического имитационного моделирования в программной среде MathCad найдены зависимости квантилей этого распределения от количества точек потока Пуассона. Это позволило свести задачу обнаружения периодичности к проверке статистической гипотезы о том, что наблюдаемая реализация потока является пуассоновской, то есть не содержит периодичности.

Для иллюстрации возможностей применения предложенного метода при решении практических задач рассчитаны вероятностные характеристики обнаружения периодичности.

Предложенная процедура обнаружения периодичности может найти применение в системах пассивной радиолокации и системах радионаблюдения, а также в прикладных задачах, связанных с исследованием свойств случайных потоков.

Ключевые слова: случайный поток, децимация, вобуляция, суперпозиция потоков, вероятность обнаружения, вероятность ложной тревоги, характеристики обнаружения, пассивная радиолокация, радионаблюдение.

Abstract: The article is devoted to the development of the method of periodic component detection in a random stream in the terms of prior uncertainty regarding stream parameters and impossibility of multiple observations of stream realizations. Available for observation stream realization is the superposition of decimated periodic stream with interval wobbulation and Poisson arrival.

To enhance the periodic component of the stream a method of point stream conversion into delta function is proposed. The amplitude spectrum of the converted stream is the spectral function (SF) of the original stream.

It is shown that the density of the probability distribution of the global maximum of Poisson arrival SF is well approximated by an alpha distribution. The relations of quantiles of this distribution to the number of points of Poisson arrival are found by the method of statistical simulation in software MathCad. This allowed to reducе the problem of detecting periodicity to the verification of statistical hypotheses that the observed realization of the stream is Poisson, i.e. contains no periodicity.

To illustrate the potential application of the proposed method in solving practical tasks, probabilistic characteristics of detection of periodicity have been calculated.

The proposed procedure for the periodicity detection may be used in passive radar systems and radio observations systems, as well as in practical tasks related to the random streams properties research.

Key words: random stream, decimation, wobble, superposition of streams, acquisition probability, false-alarm probability, detection performances, passive radiolocation, radio tracking.

Введение

Случайные (точечные) потоки широко используются в качестве моделей процессов в теории массового обслуживания, теории надежности, в прикладных задачах радиолокации и связи, биологии, сейсмологии и многих других областях.

В зависимости от конкретной задачи случайный поток можно рассматривать как входной процесс, воздействующий на систему, либо как процесс, содержащий информацию. В первом случае исследуется система, подверженная воздействию потока. Во втором - анализируется сам поток с целью извлечения полезной информации об объекте, являющимся источником потока. Информацию о свойствах источника содержат такие показатели как интенсивность потока, плотность распределения вероятности интервала между точками потока и т. п. Их оценка в стационарных условиях обычно выполняется посредством стандартных процедур. Более сложная задача возникает, если поток содержит информацию об изменении состояния источника или появлении новых источников, что может оказаться важным с прикладной точки зрения. Например, периодические изменение интенсивности потока может служить одним из флагов катастроф [1].

Появление нового источника можно рассматривать как событие, являющееся неким сигналом, что приводит к задаче обнаружения сигнала. При этом логично ожидать, что поток, порождаемый «сигнальным» источником, должен иметь неслучайные, детерминированные характеристики. В простейшем и наиболее часто встречающемся случае, сигнальный поток имеет постоянный период следования точек. Исходный источник, генерирующий случайный поток, можно рассматривать как источник помехи. Результирующий (входной) поток может оказаться либо суперпозицией случайного и периодического потоков, либо только случайным потоком. Таким образом, задача обнаружения факта наличия сигнала может быть сведена к обнаружению периодичности.

Исследованию задач выявления скрытых периодичностей во временных рядах посвящены многочисленные публикации. Разработан арсенал эффективных методов ее решения. Что касается аналогичных задач применительно к точечным потокам, то здесь результаты гораздо скромнее. Это, на наш взгляд, объясняется, с одной стороны, спецификой широкого класса прикладных задач, где наличие периодичности не рассматривается как первостепенный по значимости фактор. С другой стороны, анализ случайных потоков является методически более сложным, чем исследование временных рядов.

Трудности решения задачи обнаружения периодической составляющей потока усугубляются и тем, что периодический поток на самом деле может оказаться не совсем периодическим. Под действием неких мешающих факторов часть точек может быть потеряна (децимация или прореживание потока), а интервал между точками может быть не постоянным, равным периоду, а случайным (вобуляция периода). Кроме того, в распоряжении наблюдателя обычно находится только одна реализация входного потока (невозможность наблюдения ансамбля реализаций) и априорная информация о периодическом потоке отсутствует.

Цель настоящей работы состоит в разработке метода обнаружения периодической составляющей в случайном потоке в условиях априорной неопределенности относительно параметров потока, невозможности многократного наблюдения реализаций потока при следующих допущениях:

1) случайный поток (помеха) – простейший (Пуассоновский) поток с неизвестной интенсивностью;

2) периодический поток подвергается независимой, равновероятной децимации, т. е. каждая из точек потока может быть исключена с вероятность независимо от судьбы остальных точек;

3) точки периодического потока вобулированы относительно реперных точек, следующих с постоянным периодом.

Таким образом, доступная для наблюдения реализация потока представляет собой суперпозицию децимированного периодического потока с вобуляцией периода и простейшего потока .

Возможны два альтернативных случая:

1) представленная для анализа реализация не содержит периодической составляющей и является реализацией простейшего потока: ;

2) реализация является суперпозицией периодического и случайного потоков:.

Очевидно, задача обнаружения периодичности сводится к проверке альтернативных гипотез:

- периодическая составляющая отсутствует;

- в составе потока есть периодическая составляющая.[1]

Прежде чем перейти к содержательной части работы, уточним модель исследуемого процесса – суперпозиции периодического с случайного потоков.

Модель случайного потока

Формальная запись реализации периодического потока имеет вид:

, (1)

где - период следования точек потока; - эпоха; - плотность распределения эпохи; - размер периодического потока.

Точки потока (1) можно рассматривать как реперные. Девиация периода осуществляется относительно этих точек. Тогда поток с девиацией описывается соотношением:

, (2)

где - плотность распределения случайной величины .

Реализации децимированного потока соответствует вектор

, (3)

здесь - случайная величина, принимающая значения 0; 1 и имитирующая децимацию точек потока с вероятностью .

Реализация простейшего потока с экспоненциальным распределением интервалов между точками задается соотношением:

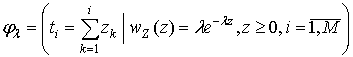
где - плотность распределения случайной величины , а - интенсивность потока; - размер случайного потока.

Суперпозиция потоков образуется в результате их временного перекрытия и формально задается как

где оператор возвращает массив, образованный размещением A, B, C, ... сверху вниз; A, B, C, ... — массивы с одинаковым числом столбцов; оператор возвращает вектор со значениями из v, упорядоченными по возрастанию.

Имитационная модель

Поставленная задача решена с использованием метода численного имитационного моделирования. Модель имитирует реализации периодического и простейшего потоков, их суперпозиции, а так же выполняет необходимые для расчета статистических оценок вычисления. Подробно модель описана в [2]. Здесь отметим лишь основные моменты.

Условные обозначения исходных данных:

– объем выборки;

- размер периодического потока (количество точек);

- период следования точек периодического потока;

- максимальное значение эпохи;

- вероятность децимации;

- коэффициент вобуляции , где при вобуляции по нормальному закону со средним квадратическим отклонением ; при вобуляции по равномерному закону на интервале ;

- интенсивность простейшего потока.

Формирование потоков.

Периодический поток с децимацией и равномерной вобуляцией периода:

, ,;

где [2] - й вектор матрицы децимирующих коэффициентов; [3] - вектор эпох - случайных величин с равномерным распределениям в интервале ; - - й вектор матрицы случайных величин, имитирующих вобуляцию периода.

Простейший поток .

, ,

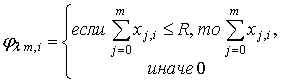где - количество точек потока Пуассона, [4] - -й вектор случайных экспоненциально распределенных с параметром .

Суперпозиция потоков .

Суперпозиции есть матрица размера :

Нормирование потоков

Результирующий поток зависит от многих параметров, большая часть которых по условию задачи, неизвестна. Для упрощения задачи желательно уменьшить их число. Можно показать, что интенсивность простейшего потока можно исключить, если нормировать интервал наблюдения и точки потока:

, (4)

где - точки потока, упорядоченные по возрастанию.

Интервалы между соседними точками распределены по экспоненциальному закону с параметром , где - математическое ожидание длительности интервалов. Интервалы нормированного потока равны , а его интенсивность

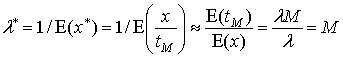то есть интенсивность нормированного потока помехи равна его размеру – количеству точек.

Постановка задачи

Количество точек потока всегда доступно наблюдателю. Поэтому если удастся найти зависимость плотности распределения некоторого параметра нормированного простейшего потока от размера , то процедура обнаружения периодической составляющей может быть сведена к проверке статистической гипотезы о незначимом отличии плотности распределения параметра нормированной суперпозиции потоков от плотности простейшего потока. При выполнении нулевой гипотезы принимается решение об отсутствии в суперпозиции периодической составляющей. Здесь - уровень значимости.

Альтернативной гипотезе соответствует решение о наличии периодической составляющей (сигнала).

Отметим, что количество точек суперпозиции равно , где и - размеры периодического и простейшего потоков соответственно. Для потока помехи . Плотность зависит от одного параметра , в то время как плотность от и , которые могут принимать все возможные значения, удовлетворяющие равенству . Это обстоятельство делает проблематичной возможность нахождения плотности распределения . Во всяком случае, в настоящей работе эта задача не решена и плотность неизвестна. Этот факт не влияет на процедуру проверки гипотезы , но делает невозможным нахождение вероятности правильного обнаружения сигнала. Однако при имитационном моделировании можно найти оценку этой вероятности, как частоту принятия альтернативной гипотезы .

Поскольку уровень значимости есть вероятность отклонения верной гипотезы , то есть принятие решения о наличии сигнала, когда на самом деле его нет, то вероятность ложной тревоги равна .

Преобразование потоков

Точечные потоки плохо приспособлены к непосредственному анализу при решении задач обнаружения периодичности. Поэтому потоки преобразуют либо к привычному виду временных рядов [1] для их последующего анализа методами теории сигналов, либо используют преобразования, позволяющие усилить периодические составляющие в преобразованном процессе [3].

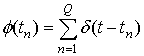В [2] предложен подход, состоящий в преобразовании исходного потока точек в поток -функций . Для полученного потока вычисляются косинус- и синус-преобразования Фурье:

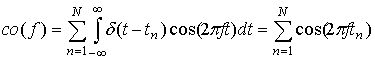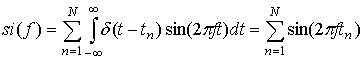и амплитудный спектр:

(5)

Амплитудный спектр, однозначно связан с исходным потоком, поэтому его можно рассматривать как спектральную функцию (СФ) потока точек. В [2] доказано, что СФ обладает селектирующей способностью.

Выбор параметра обнаружения

При выборе параметра будем исходить из следующих соображений. Во-первых, он должен обладать как можно большей контрастностью – разностью между его значениями при наличии и отсутствии сигнала. Во-вторых, он должен быть доступен для вычисления по одной реализации потока.

Обратимся сначала к визуальному анализу СФ суперпозиции сигнала и помехи () и помехи (). На рис. 1 приведены графики СФ случайных реализаций нормированных потоков. Очевидно, что главное различие проявляется в величинах глобальных максимумов. Однако, при иных параметрах сигнала и помехи может оказаться, что различие в глобальных максимумах не столь выражено. Поэтому в качестве других претендентов на роль параметра рассмотрим средние значения , и средние квадратические отклонения (с.к.о.) , спектральных функций.

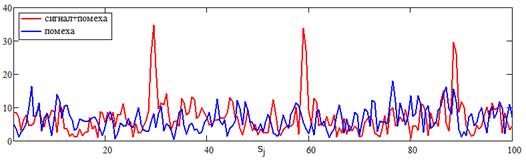
Рис. 1. Амплитудные спектры случайных реализаций потоков.
Параметры модели: , , , .

На рис. 2. приведены графики значений глобальных максимумов , , средних значений , и с.к.о. , СФ реализаций потоков. Видно, что области значений глобальных максимумов и с.к.о. достаточно хорошо разделены, в то время как области средних значений почти перекрываются. В связи с этим, средние значения СФ исключим из дальнейшего рассмотрения.

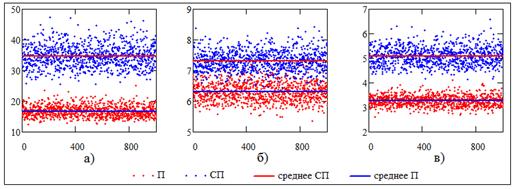
Рис. 2. Ансамбль реализаций числовых характеристик СФ помехи (П) и смеси сигнала и помехи (СП):
а) глобальные максимумы СФ; б) средние значения СФ;
в) с. к. о. СФ. Параметры модели: , , ,

Для более обоснованного выбора параметра обнаружения рассчитаем объективные показатели.

Вероятность ошибки обнаружения[5]

Имитационная модель позволяет рассчитать зависимость вероятности ошибки обнаружения от порога и найти ее минимальное значение. Для этого по ансамблю реализаций потоков находим выборочные функции распределения вероятности параметров СФ:

- функция распределения параметра ( или ) СФ суперпозиции сигнала и помехи;

- функция распределения параметра ( или ) СФ и помехи;

- порог обнаружения.

Вероятность ошибки вычисляется по формуле:

. (6)

Минимум вероятности ошибки равен , где - оптимальный порог обнаружения.

На рис. 3 приведены графики вероятностей ошибки для конкретных параметров модели.

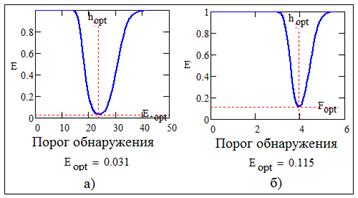
Рис. 3. Зависимость вероятности ошибки от величины порога обнаружения при:
а) обнаружении по глобальному максимуму СФ;
б) обнаружении по с. к. о. СФ. Параметры модели: , , , .

Отношение средних значений

Другим показателем сравнения может служить отношение средних значений параметров обнаружения ( ,) при наличии и отсутствии сигнала (периодической составляющей):

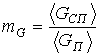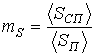, . (7)

Здесь угловые скобки означают усреднение по ансамблю.

Характеристики обнаружения зависят от параметра помехи (размера потока ) и параметров сигнала (размера периодического потока, вероятности децимации и коэффициента вобуляции ). На рис. 4…6 приведены графики вероятностей , и коэффициентов , .

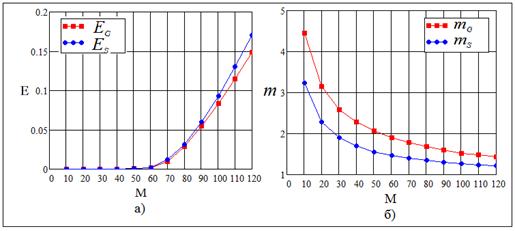
Рис. 4. Зависимость характеристик от размера потока помехи:
а) вероятность суммарной ошибки при обнаружению по глобальному максимуму () и с. к. о. ();
б) отношение средних значений глобальных максимумов () и с. к. о. ().
Параметры модели: , , .

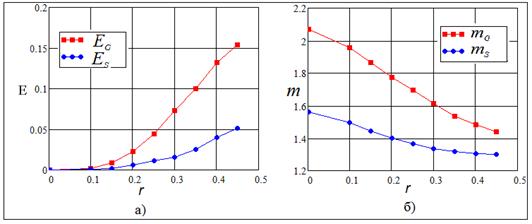
Рис. 5. Зависимость характеристик от коэффициента вобуляции периодического потока:
а) вероятность суммарной ошибки при обнаружении по глобальному максимуму () и с. к. о. ();
б) отношение средних значений глобальных максимумов () и с. к. о. ().
Параметры модели: , .

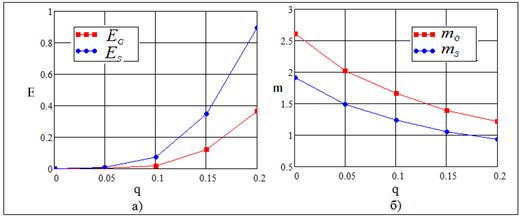
Рис. 6. Зависимость характеристик от вероятности децимации периодического потока:
а) вероятность суммарной ошибки при обнаружению по глобальному максимуму () и с. к. о. ();
б) отношение средних значений глобальных максимумов () и с. к. о. ().
Параметры модели: ,. .

Предпочтение следует отдать тому параметру обнаружения, при котором вероятность ошибки меньше, а отношение средних больше. Для случая обнаружения по глобальному максимуму эти условия не выполняются только для вероятности ошибки при варьировании коэффициента вобуляции (см. рис. 4…6). Поэтому предпочтение следует отдать обнаружению по глобальному максимуму.

Плотность распределения вероятности глобального максимума СФ нормированного простейшего потока

Для проверки гипотезы H₀ о том, что наблюдаемая реализация нормированного потока является Пуассоновской, необходимо найти плотность распределения вероятности глобальных максимумов СФ. Вследствие нелинейной зависимости СФ и ее глобального максимума от параметров потока не удается найти теоретическое распределение плотности. Асимптотические методы теории статистики экстремальных значений в нашем случае оказались неприемлемы [4]. Поэтому решение пришлось искать методами численного моделирования. Сформированы ансамбли реализаций простейшего потока. Для каждой реализации рассчитана СФ и найден ее глобальный максимум, по множеству которых построены гистограммы. Оказалось, что оценочные распределения достаточно хорошо аппроксимируются - распределением[6] с плотностью [5]

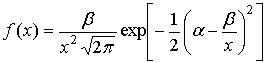(8)

и функцией распределения

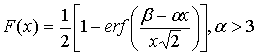. (9)

Гипотеза об - распределении проверялась по критерию омега-квадрат при для потоков размера при объеме выборки =10⁴. Во всех случаях оказалось, что уровень значимости не меньше 0.4, что говорит о допустимости аппроксимации.

Статистическая оценка параметров - распределения

Параметры распределения.

При проверке гипотезы H₀ о простейшем потоке нужно знать зависимость плотности распределения глобальных максимумов от размера потока , т. е. зависимости коэффициентов , .

Параметры распределения рассчитываются по формулам:

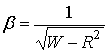, (10)

где . .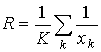

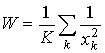Математическое ожидание и дисперсия соответственно равны:

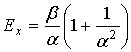, (11)

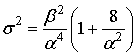. (12)

Из системы уравнений (11), (12) можно найти иные, чем в (10), формулы для параметров распределения:

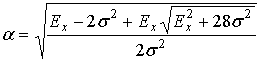, (13)

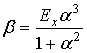. (14)

Методом имитационного моделирования найдены зависимости оценок среднего , дисперсии и параметров , от размера потока . По этим оценкам можно найти зависимости коэффициентов , . Оказалось, что результаты расчетов по формулам (10) очень чувствительны к точности аппроксимации зависимостей и . Более надежные результаты получаются при расчетах по формулам (13) и (14).

Зависимости и хорошо аппроксимируются[7] следующими выражениями:

, (15)

. (16)

Подставив формулы (15) и (16) в (13) и (14) получим зависимости параметров распределения , от размера потока.

Квантили распределения.

Для проверки гипотезы H₀ необходимо найти квантили - распределения, которые равны корню уравнения

, (17)

где - уровень значимости.

Уравнение (17) решалось численным методом при и =0.2; 0.15; 0.1; 0.05; 0.01; 0.005; 0.001.

Зависимости квантилей от размера потока хорошо аппроксимируются степенной функцией:

(18)

Значения коэффициентов приведены в табл. 1.

Таблица 1

Уровень значимости	Коэффициент a	Коэффициент b	Коэффициент детерминации
0.8	2.2525	0.5345	0.9999
0.85	2.2768	0.5374	0.9999
0.9	2.3071	0.5413	0.9997
0.95	2.3529	0.5474	0.9995
0.99	2.4404	0.5605	0.9989
0.995	2.4728	0.5658	0.9987
0.999	2.5420	0.5778	0.9979

Процедура обнаружения факта наличия периодичности

Рассмотрим последовательность действий при обнаружении периодичности потока при заданной вероятности ложного обнаружения .

Пусть в распоряжении наблюдателя имеется реализация потока – множество чисел, упорядоченных по возрастанию: .

Шаг 1. Нормирование потока .

Шаг 1. Расчет спектральной функции потока

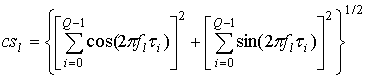, (19)

где , , [8].

В преобразовании (19) переменная имеет смысл времени, а - частоты. Поэтому - минимальный и максимальный периоды точек нормированного потока, а - шаг дискретизации периода. Имитационное моделирование, посредством которого найдены зависимости (15), (16), (18), выполнялось при =2, =100 и =0.5. Поэтому и при проверке гипотезы относительно конкретных потоков следует задавать те же параметры, что и при моделировании.

Шаг 3. Нахождение глобального максимума спектральной функции

[9]. (20)

Шаг 4.

Вычисление по формуле (18) квантиля на уровне значимости и сравнение его с глобальным максимумом . При гипотеза H₀ о незначимом отличии потока от Пуассоновского отклоняется и принимается альтернативная гипотеза H₁ – в составе потока присутствует периодическая составляющая.

В табл. 1 приведены коэффициенты аппроксимирующей функции для ограниченного числа значений уровня значимости. На практике может потребоваться проверка гипотезы для иных значений . В этом случае следует величину глобального максимума рассматривать как квантиль, а соответствующую ему вероятность находим по формуле:

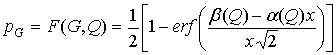. (21)

Гипотеза H₀ отклоняется, если .

Результаты имитационного моделирования

Для оценки возможности применения предложенного метода обнаружения факта наличия периодичности методом имитационного моделирования найдены вероятностные характеристики обнаружения.

Оценки вероятностей рассчитывались по формуле:

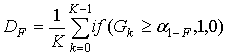[10],

где - объем выборки, - глобальный максимум СФ -й реализации потока.

На рис. 7…9 приведены зависимости вероятности обнаружения периодичности от размеров и периодического и простейшего потоков, вероятности децимации и коэффициента вобуляции. Расчеты проводились по выборке объема =5000. Рассматривалось влияние одного фактора при незначимом влиянии остальных.

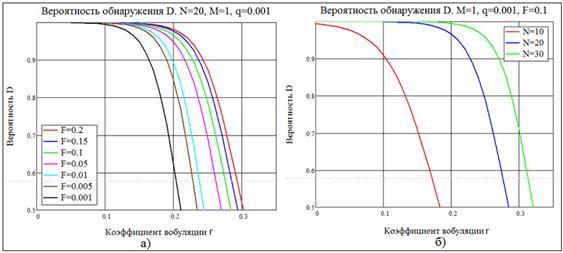
Рис. 7. Зависимость вероятности обнаружения от коэффициента вобуляции:
а) при различных вероятностях ложного обнаружения и постоянном размере периодического потока;
б) при фиксированной вероятности и разных размерах .

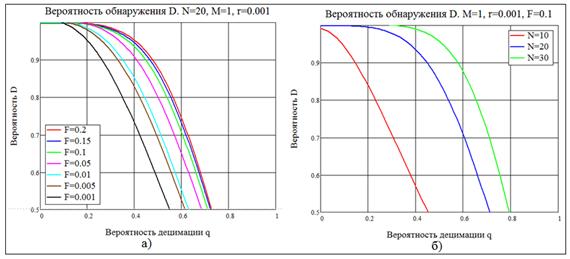
Рис. 8. Зависимость вероятности обнаружения от вероятности децимации потока:
а) при различных вероятностях ложного обнаружения и постоянном размере периодического потока;
б) при фиксированной вероятности и разных размерах .

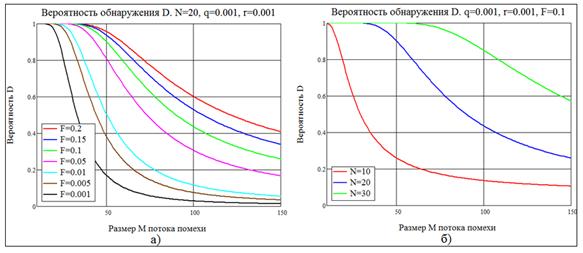
Рис. 9. Рис. 8. Зависимость вероятности обнаружения от размера простейшего потока:
а) при различных вероятностях ложного обнаружения и постоянном размере периодического потока;
б) при фиксированной вероятности и разных размерах .

Результаты моделирования подтверждают работоспособность предложенной процедуры обнаружения периодичности. Как и следовало ожидать, в условиях практически полной априорной неопределенности характеристики обнаружения оказались не слишком хорошими: вероятность обнаружения довольно быстро уменьшается по мере увеличения интенсивности мешающих факторов. Вместе с тем результаты могут оказаться приемлемыми, если стоимость риска ложного обнаружения невелика. Кардинальное улучшение характеристик возможно, на наш взгляд, лишь при увеличении объема априорной информации.

Заключение

Предложен метод обнаружения скрытой периодичности в случайном потоке точек в условиях априорной неопределенности. Показана его применимость при обнаружении периодичности по единственной реализации потока.

Аппроксимирующие функции (15), (16) и (18) найдены по репрезентативным выборкам большого объема и могут быть использованы при обнаружении периодичности в достаточно широком диапазоне значений размера потока.

Литература

1. Любушин А.А. Анализ данных систем геофизического и экологического мониторинга / А.А.Любушин; отв. ред. Г.А. Соболев; Ин-т физики Земли им. О.Ю. Шмидта РАН. – М.: Наука, 2007. – 228 с. – ISBN 5-02-034063-4 (в пер.)

2. Голик Ф. В. Характеристики обнаружения периодического потока с независимой децимацией в суперпозиции с простейшим потоком. // Журнал радиоэлектроники: электронный журнал. 2015. N 8. URL: http://jre.cplire.ru/jre/aug15/4/text.html, http://jre.cplire.ru/jre/aug15/4/text.pdf

3. Серебряков М.Г., Первозванский А.А. Выявление скрытых периодичностей. - М.: Наука, 1965. - 244 с.

4. Лидбеттер М., Линдгрен Г., Ротсен X. Экстремумы случайных последовательностей и процессов/. — М.: Мир, 1989.—392 с, ил.

5. Случайные процессы в параметрических моделях надежности / Переверзев Е. С.- Киев: Наук. думка, 1987. – 240 с.

[1]Наличие периодической составляющей можно рассматривать как факт присутствия сигнала, а процедуру проверки гипотезы Н₁ как обнаружение сигнала. В этой связи логично использовать устоявшуюся в радиотехнике терминологию. В дальнейшем, там, где это, возможно, будем говорить вместо «периодический поток» - «сигнал», а вместо «простейший поток» - «помеха», а вместо «суперпозиция потоков» – «смесь сигнала и помехи» (СП).

[2] rbinom(m, n, p) -возвращает вектор из m случайных чисел, имеющих биномиальное распределение с размером n и вероятностью успеха p.

[3] runif(m, a, b) - возвращает вектор из m случайных чисел, имеющих равномерное распределение на интервале [a,b].

[4] rexp(m, r) - возвращает вектор из m случайных чисел, имеющих экспоненциальное распределение с коэффициентом r.

[5] Вероятность ошибки обнаружения равна сумме вероятностей пропуска сигнала и вероятности ложного обнаружения.

[6] В [2] распределение глобального максимума ненормированного потока аппроксимировалось нормальным распределением. Для нормированного потока аппроксимация - распределением оказалась более надежной.

[7] Коэффициенты детерминации равны 0.9999.

[8] floor(z) - возвращает наибольшее целое, меньшее или равное z.

[9] max(A, B, C, ...) - возвращает наибольшее из значений A, B, C, …

[10] if(cond, x, y) - возвращает x, если истинно логическое условие cond (не равно нулю), иначе возвращает y.