Комплементарная множественная декомпозиция на эмпирические моды с адаптивным шумом CEEMDAN как метод решения основных проблем применения преобразования Гильберта-Хуанга.

УДК 51-7:612.16

Комплементарная множественная декомпозиция на эмпирические моды с адаптивным шумом CEEMDAN как метод решения основных проблем применения преобразования Гильберта-Хуанга

В. Д. Омпоков, В. В. Бороноев

Институт физического материаловедения СО РАН

Статья поступила в редакцию 21 сентябяря 2016 г.

Аннотация. Статья посвящена методу множественной эмпирической модовой декомпозиции сигналов с адаптивным шумом, позволяющему решать основные проблемы применения преобразования Гильберта-Хуанга в задаче обработки и анализа биомедицинских сигналов. Отмечено, что в результате декомпозиции пульсового сигнала на эмпирические моды часто получаются функции с перекрывающимися частотными диапазонами и происходит так называемый “модовый переход”, что затрудняет анализ спектрального состава сигнала. Для решения этих проблем реализован алгоритм множественной эмпирической модовой декомпозиции сигналов с адаптивным шумом (CEEMDAN), суть которой заключается в многократном добавлении к сигналу белого шума.

Ключевые слова: пульсовой сигнал, преобразование Гильберта-Хуанга, множественная эмпирическая модовая декомпозиция с адаптивным шумом.

Abstract. The most promising method of time-frequency analysis of the data is the Hilbert-Huang Transform, which makes it possible to work with nonstationary and nonlinear data. The method is based on the Empirical Mode Decomposition of signals and the Hilbert Transform. The key feature of Empirical Mode Decomposition is to decompose a signal into so-called Intrinsic Mode Function (IMF). IMF represents a simple oscillatory mode as a counterpart to the simple harmonic function, but it is much more general: instead of constant amplitude and frequency in a simple harmonic component, an IMF can have variable amplitude and frequency along the time axis. Further-more, the Hilbert Spectral Analysis of Intrinsic Mode Functions provides frequency information evolving with time and quantifies the amount of variation due to oscillation at different time scales and time locations. The paper shows problems solving of applying Hilbert-Huang Transform for biomedical signal processing. It is the presence of oscillations of very disparate amplitude in a mode, or the presence of very similar oscillations in different modes. Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (CEEMDAN) can effectively overcome these problems, and potentially should provide more objective results than alternative methods. In the CEEMDAN method a particular noise is added at each stage of the decomposition and a unique residue is computed to obtain each mode.

Key words: pulse signal, Hilbert-Huang transform, Complete Ensemble Empirical Mode Decomposition with Adaptive Noise.

Одним из наиболее перспективных методов исследования нестационарных и нелинейных сигналов является метод, основанный на модовой декомпозиции сигналов и преобразовании Гильберта. Преобразование Гильберта-Хуанга позволяет исследовать динамику изменения мгновенных частот и их амплитуд, что особенно важно при изучении биомедицинских сигналов с меняющимися во времени характеристиками, поскольку появляется возможность анализировать свойства сигнала одновременно во временном и в частотном пространствах с возможностью выявления дополнительных диагностических признаков, приводящих к повышению точности постановки врачом диагноза. Преобразование Гильберта-Хуанга представляет собой частотно-временной анализ данных (сигналов) и не требует априорного функционального базиса преобразования. Метод был предложен Норденом Хуангом в 1995 с обобщением на анализ произвольных временных рядов коллективом соавторов в 1998 г. [1,2,3]. Достоинством является высокая адаптивность, связанная с тем, что базисные функции для разложения сигнала конструируются непосредственно из самого исследуемого сигнала.

Преобразование Гильберта-Хуанга состоит из двух этапов. На первом этапе при помощи метода эмпирической модовой декомпозиции происходит разложение наблюдаемого процесса на отдельные составляющие (моды). Затем, на втором этапе при помощи преобразования Гильберта полученных компонент разложения, определяется мгновенный спектр наблюдаемого процесса.

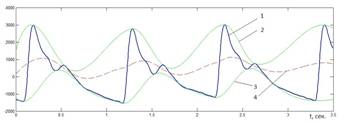
В основе алгоритма эмпирической модовой декомпозиции лежит построение гладких огибающих по максимумам и минимумам последовательности и дальнейшее вычитание среднего этих огибающих из исходной последовательности. Для этого производится поиск максимумов и минимумов и методом сплайн аппроксимации этих точек определяются верхняя и нижняя огибающие. На рисунке 1 представлены анализируемая последовательность f(x) (кривая 1), огибающая максимумов и огибающая минимумов (кривые 2 и 3 соответственно). Пунктирной линией представлена средняя линия m1(x) (кривая 4), которая вычисляется по огибающим 2 и 3:

Рис. 1. Построение огибающих и средней линии пульсового сигнала

Более подробно алгоритм преобразования Гильберта-Хуанга при исследовании пульсовых сигналов представлен в работах [4, 5].

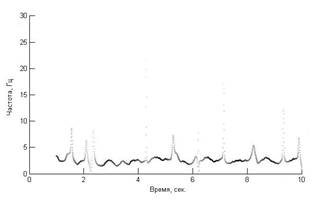
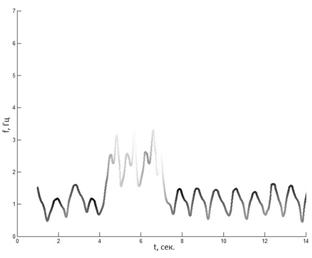
В данной же работе представлено решение основных проблем применения преобразования Гильберта-Хуанга в задаче обработки и анализа пульсовых сигналов. Так, в результате декомпозиции пульсового сигнала на эмпирические моды часто получаются функции со схожими частотными характеристиками, что затрудняет анализ спектрального состава сигнала. Например, на рис.2 представлено частотно-временное распределение двух модовых функций одного и того же сигнала, где видно, что колебания происходят примерно в одной полосе частот.


Рис.2. Спектр Гильберта двух модовых функций с одинаковой полосой частот

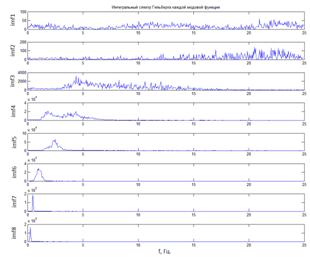
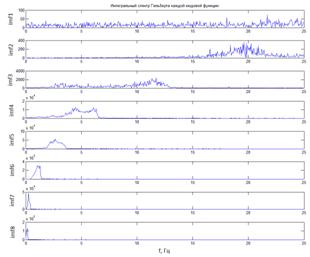
На рис.3 представлен интегральный спектр Гильберта каждой модовой функции, где показано, что частотный диапазон одной модовой функции перекрывает частотный диапазон другой модовой функции (imf4 и imf5). Чтобы иметь полную картину частотно-временного распределения в этой полосе частот нужно будет анализировать представленный спектр обеих модовых функций по отдельности или их сумму. Чтобы отойти от такого рода избыточности в выделении модовых функций необходимо выделять модовые функции таким образом, чтобы их частотные диапазоны, по возможности, не пересекались.


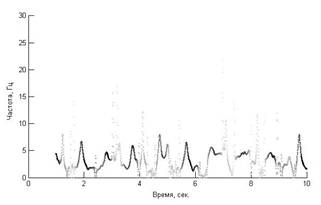
Рис.3. Интегральный спектр Гильберта	Рис.4. Спектр Гильберта 5-й модовой функции

Следующей проблемой является и то, что на некоторых временных отрезках наблюдаются колебания с частотами, не характерными для данной модовой функции. Например, на рис.4 на пятой модовой функции imf5 на временном отрезке от 4,5 до 7 секунд частота колебаний в 2 раза выше, чем на остальных участках. Т.е. на этом временном отрезке произошел т.н. модовый переход из соседней модовой функции.

Для решения выявленных проблем реализован алгоритм множественной эмпирической модовой декомпозиции [6, 7]. Суть алгоритма заключается в многократном добавлении к сигналу белого шума и вычислении среднего значения модовых функций как конечного истинного результата. Поскольку преобразование Гильберта-Хуанга предполагает определение точек экстремумов сигнала и построение огибающих по этим точкам, то при добавлении белого шума появляются дополнительные точки экстремумов, которые позволяет лучше описать сигнал:

1. формируется массив из I реализаций: xⁱ(t)=x(t)+a*wⁱ, i=1..I, где x(t) – исходный сигнал, wⁱ – I реализаций белого шума, a – уровень шума.

2. для каждой реализации как отдельного процесса определяются модовые функции , i=1..I, k=1..K, где K – количество модовых функций.

3. расчет средней модовой функции как конечного результата.

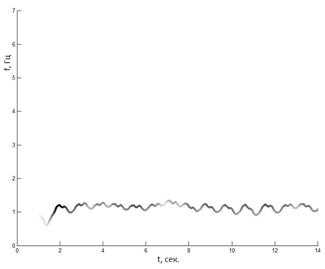
На рис. 5 и 6 представлены результаты работы данного алгоритма, которые показывают его эффективность при обработке пульсовых сигналов. На рис. 5 представлен интегральный спектр Гильберта модовых функций, где показано, что частотные диапазоны модовых функции практически не пересекаются, за исключением шумов. На рис.6 отсутствуют колебания с нехарактерными для данной кривой параметрами.


Рис.5. Интегральный спектр Гильберта	Рис.6. Спектр Гильберта 6-й модовой функции

В данной работе представлен новый алгоритм эмпирической модовой декомпозиции сигналов [6, 7], позволяющий извлекать информацию о меняющихся во времени характеристиках процесса в условиях нестационарной динамики и при наличии помех. Большое практическое значение имеет применение данного метода для обработки и анализа биомедицинских сигналов, в т.ч. и пульсовых [4, 5]. Показано, что представленный метод позволяет производить декомпозицию сигнала на набор модовых функций с практически неперекрывающимся частотным диапазоном и уменьшает так называемый “модовый переход”. Практическое применение данного алгоритма позволило существенно расширить возможности адекватной расшифровки информации, содержащейся в экспериментальных данных.

Литература

1. Norden E. Huang, Samuel S.P. Shen. The Hilbert-Huang transform and its applications // World Scientific Publishing Co. Pte. Ltd. 2005. 311 p.

2. Norden Huang et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proceedings of the Royal Society of London. A 454, 903–995 (1998).

3. An Introduction to Hilbert-Huang Transform: A Plea for Adaptive Data Analysis. Norden E. Huang. Research Center for Adaptive Data Analysis. National Central University.

4. Бороноев В.В., Омпоков В.Д. Возможности преобразования Гильберта-Хуанга в задаче обработки и анализа биомедицинских сигналов // Биомедицинская радиоэлектроника. 2014. №3. С. 40-44.

5. Boronoev V.V.; Ompokov V.D. The Hilbert-Huang Transform for biomedical signals processing // Proceedings of International Conference on Computer Technologies in Physical and Engineering Applications (ICCTPEA). St. Petersburg, 2014. P. 21-22. URL:

http://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=6893255.

6. Zhaohua Wu, Norden E. Huang. Ensemble Empirical Mode Decomposition: A Noise Assisted Data Analysis Method. Advances in Adaptive Data Analysis Vol.1, No.1 (2009) 1–41

7. María E. Torres, Marcelo A. Colominas; Gastón Schlotthauer, Patrick Flandrin. A complete ensemble empirical mode decomposition with adaptive noise // 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP) - 22-27 May 2011, Prague, P. 4144-4147.