О МЕТОДЕ РАЗДЕЛЕНИЯ ВО ВРЕМЕНИ АВТОКОРРЕЛЯЦИОННЫХ ГАРМОНИЧЕСКИХ СОСТАВЛЯЮЩИХ ШИРОКОПОЛОСНЫХ СИГНАЛОВ

А. Ю. Гришенцев

Федеральное государственное автономное образовательное учреждение высшего образования «Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики»

Статья поступила в редакцию 26 июля 2016 г.

Аннотация. По определению широкополосной называется связь, в которой сообщения удовлетворяют следующему условию: FT ≫ 1, где Т – длительность сообщения F – полоса частот, занимаемая сообщением. Многообразие областей применения и возможностей широкополосной связи определяет специфику различных способов реализации. Технологии широкополосной связи имеют более чем шестидесятилетнюю историю, первые разработки (вторая половина тридцатых годов XX столетия) относятся к системам военного назначения. На сегодняшний день системы широкополосной связи используются практически во всех направлениях информационной коммуникации. Данная работа посвящена методу распознавания сообщений в системах широкополосной радиосвязи, предлагаемый метод реализует разделение во времени автокорреляционных гармонических составляющих широкополосных сигналов. Во введении приведены ссылки на серию публикаций, посвящённых вопросам поиска и обработки сигналов, полученных на основе автокорреляционных функций особой формы. Работа является продолжением указанных публикаций и в совокупности образует целостную методологию построения систем широкополосной связи, использующих сигналы, полученные на основе матриц с автокорреляционной функцией специального вида, имеющих комплексные значения элементов. В водной части статьи сформулированы цели и задачи исследования. Отдельное внимание уделено формулировке проблемы исследования и возможным альтернативным способам решения поставленной проблемы. В следующей части работы рассмотрен непосредственно метод разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов: приведена функциональная блок-схема реализации метода, подробно изложена и обоснованна последовательность всех преобразований. Далее рассмотрены некоторые результаты, полученные при практической реализации метода, произведено сравнение с возможными альтернативными решениями. В заключении работы сформулированы итоги, отмечены преимущества разработанного метода, в частности показано, что предложенный метод позволяет эффективно разделять автокорреляционные составляющие распознаваемых сообщений, при распознавании имеется возможность использовать весь частотно-временной ансамбль сообщения, а следовательно использовать все преимущества сигналов, сформированных на основе матриц с автокорреляционной функцией специального вида, имеющих комплексные значения элементов.

Ключевые слова: кодовое разделение сигналов, радиосвязь, цифровая обработка сигналов, автокорреляционная функция.

Abstract. By definition, wideband refers to the communication in which messages satisfy the following condition: FT ≫ 1, where T - duration of the message the F - band occupied by the message. The variety of applications and wideband capabilities determines the specificity of the different methods of implementation. Wideband technologies are more than sixty years of history, the first development (the second half of the thirties of the XX century) relates to systems for military use. Today, wideband systems are used in virtually all areas of information communication.
This work is devoted to posts recognition method in a wideband wireless systems, the proposed method realizes the separation in time of the autocorrelation of the harmonic components of wideband signals. The introduction includes links to a series of publications devoted to the issues of search and processing of signals received on the basis of a special form of autocorrelation functions. The work is a continuation of these publications, and together they form a complete methodology for the construction of wideband systems using signals obtained on the basis of matrices with the autocorrelation function of a special form with complex values ​​of the elements. The water of this article set out the aims and objectives of the study. Special attention is paid to the formulation of research problems and possible alternative ways of solving the problem. In the next part of the paper directly to the method of separation in time of the autocorrelation of the harmonic components of wideband signals: a functional block diagram of an implementation of the method, described in detail and justified sequence of transformations. Next, we consider some of the results obtained in the practice of the method, a comparison with possible alternative solutions. At the end of the work set forth the results, noted the advantages of this method, in particular, it is shown that the proposed method can effectively divide the autocorrelation components recognizable messages, with the recognition it is possible to use the entire time-frequency band communication, and thus take advantage of the signals generated in the matrix basis with autocorrelation the function of a special form with complex values ​​of the elements.

Keywords: code division signals, radio communications, digital signal processing, autocorrelation function.

 

Введение

Актуальной проблемой радиосвязи [1] является разработка методов и технологий распознавания сообщений при скрытой, подшумовой передаче сигналов. Как в системах, неспособных обеспечить надшумовую передачу, например, в результате ограничения мощности передатчика и при значительном удалении от приёмника, примером может быть связь с космическими аппаратами, так и в случае намеренно скрытой в шуме радиоэфира передачи информации, например, в системах военной связи.

Данная работа является логическим продолжением комплекса исследований, освещённых в публикациях «Алгоритм поиска, некоторые свойства и применение матриц с комплексными значениями элементов для стеганографии и синтеза широкополосных сигналов», «Понижение размерности пространства при корреляции и свертке цифровых сигналов» и «Синтез бинарных матриц для формирования сигналов широкополосной связи», [2], [3] и [4] соответственно. В частности, в работе [2] показано, что с помощью операции корреляции возможно эффективно распознавать сигналы, сформированные на основе матриц с комплексными значениями элементов и имеющими автокорреляционные функции (АКФ) с высокими значениями в центре (для центрального элемента) и относительно небольшие для остальных (боковых) элементов, в работе [2] введен термин для обозначения класса подобных матриц: матрицы с АКФ специального вида, далее, говоря о таких матрицах, будем иметь в виду матрицы с комплексными значениями элементов.

Цели и задачи работы

Цель: разработка и исследование метода разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов.

Задачи работы:

– постановка проблемы корреляционного разделения при использовании сигналов, сформированных на основе матриц с АКФ специального вида;

– разработка метода разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов;

– моделирование разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов и анализ результатов исследования.

Проблема исследования

Известным фактом является проблема разделения сигнала на составляющие (частотные, временные, фазовые) с целью распознавания сообщений [5], [6]. Например, при использовании сигналов, сформированных на основе матриц с АКФ специального вида, при распознавании сообщения возникает проблема разделения сигнала на гармонические составляющие соответствующие мнимой и вещественной части матрицы АКФ [2]. Причём наиболее интересным решением является разделение на составляющие без частотного разделения сигнала, т.е. во временном пространстве.

Сообщением M_k(t) (где k=1…N, N – мощность алфавита) будем называть сигнал, соответствующий одному символу алфавита. Пусть чередующаяся последовательность сообщений M_k(t),  сформированных на основе матриц с АКФ специального вида, образуют сигнальные пакеты S′(t) в виде смеси гармонических составляющих,  причём: cos-ные составляющие соответствует вещественной части сигнала Re(S), а sin-ные – мнимой Im(S). Приёмное устройство принимает сигнал S(t), который возможно выразить с помощью следующей модели:

,                    (1)

где:  – свёртка исходного сигнала S′(t) с совокупной импульсной характеристикой  канала передачи сигнала;   – помеха, сосредоточенная по спектру;  – помеха, сосредоточенная по времени;   – флуктуационная помеха.

Приёмное устройство должно осуществлять приём и распознавание информационных сообщений M_k(t) в сигнале S(t) на фоне помех, для этого используется АКФ, что возможно записать как:

,                                    (2)

где  есть комплексно сопряжённое сообщение к M_k(t). Для случая, когда S(t) является искомым сообщением M_k(t), выражение (2) будем называть АКФ с некоторыми допущениями, учитывая искажения сигнала S(t) относительно S′(t) в соответствии с (1).  Выражение (2) возможно записать в компактном виде:

A_k(t)=(S●M_k)(t),                                                          (3)

где символ (●) обозначает операцию корреляция.

Эффективный расчёт АКФ комплекснозначных функций возможно производить при разделении мнимых и вещественных составляющих, как в сообщениях  , так и в сигнале S(t). Разделение составляющих в сообщениях  не представляет затруднений, т.к. полный набор заранее сформированных вещественной и мнимой компонент сообщений может храниться в приёмном устройстве. Совсем по-другому обстоит дело с сигналом S(t), в сигнале все компоненты смешаны в одну вещественную функцию. Простой расчёт АКФ на множестве вещественных чисел существенно снижает качество выделения полезных сигналов, поэтому применение автокорреляции (3) без учёта комплексной формы сообщений  и сигнала S(t), является не эффективным. Таким образом, возникает проблема разделения сигнала S(t) на вещественные и мнимые составляющие. Как будет показано дальше, фактически эту проблему возможно рассматривать как разделение АКФ  на вещественные и мнимые составляющие.

Одним из известных решений данной проблемы является частотное разделение [5], [6] сигнала S(t). Сообщения, сформированные на основе матриц с АКФ специального вида, могут иметь достаточно широкий спектр, особенно при наличии cos-ой составляющей с нулевой начальной фазой, поэтому частотное разделение, при сохранении необходимого качества сигналов, затруднительно. Также, существенные недостатки частотного разделения проявляются, когда сигнал скрыт в шуме эфира, т.е. когда осуществляется подшумовая передача, при этом на каждой частоте частотно-временного ансамбля, используемого для синтеза сигнала, уровень сигнала может быть значительно ниже уровня шума эфира, в результате распознавание сообщения по элементам, без совместного участия всего частотно-временного ансамбля, затруднено и малоэффективно, т.к. не используются все преимущества особенностей АКФ. Существенные достижения есть в поляризационном разделении сигналов [7]–[9], но возможное изменение поляризации сигнала при прохождении канала связи и недостаточная поляризационная избирательность передающего и приёмного устройств тоже снижают практическую эффективность поляризационного разделения, ограничивая область применения только каналами связи, где поляризация сигнала мало подвержена изменениям, например, в межспутниковой ретрансляционной космической связи [9].

Таким образом, актуальной является разработка методов разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов.

Предпосылки к разработке метода

Рассмотрим «механизмы» численных преобразований, происходящих при вычислении автокорреляции (3) комплексных функций. При вычислении центрального элемента АКФ происходит суммирование последовательности произведений комплексных чисел z на сопряжённые z^*, т.е.:

z∙z^*=(a+jb)∙(a–jb)=a²+jab–jab+b²=a²+b²,                   (4)

очевидно, что центральный элемент АКФ будет вещественным числом. Как показано в [2], выделение только вещественной части АКФ позволяет получать наилучший результат для распознавания сообщений. Заметим, что для наиболее эффективного распознавания сообщений центральный элемент АКФ должен иметь максимальное значение, а боковые (не центральные) элементы возможно наименьшие значения, формирование таких сигналов подробно рассмотрено в работах [1], [2] и [4]. При использовании вместо комплексных чисел вещественных, т.е. |z|, выгодная для АКФ специфика перемножения комплексных чисел будет утрачена, т.е. центральный элемент сохранит то же значение:

,                      (5)

но значения боковых лепестков АКФ возрастут за счёт добавления мнимых составляющих к вещественным. Далее сформулируем предлагаемый метод разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов.

Метод разделения во времени автокорреляционных гармонических составляющих

Основанием метода являются следующие рассуждения. При корреляции комплексных функций u=f₁●f₂, образованных суммой гармонических составляющих (в которых мнимая часть Im(f) соответствует sin-ым гармоническим составляющим, а вещественная часть Re(f) – cos-ым), вещественная часть корреляционной функции будет образованна суммами произведений sin-ых на sin-ные составляющих и cos-ых на cos-ные, что символично возможно записать как:

,                       (6)

где минус образуется в результате возведения в квадрат единичного вектора мнимой части j²=–1; мнимая составляющая будет образована суммами произведений sin-ых на cos-ные составляющих и cos-ых на sin-ные, что символично возможно записать как:

,                   (7)

в выражениях (6), (7) знаки суммы и разности означают поэлементное сложение  (вычитание) для дискретных и сложение (вычитание) во времени для непрерывных сигналов. Учитывая попарную ортогональность различных гармонических составляющих сигнала S и сообщения M_к, возможно записать следующую схему преобразования (рис. 1)  реализующую метод разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов.

 

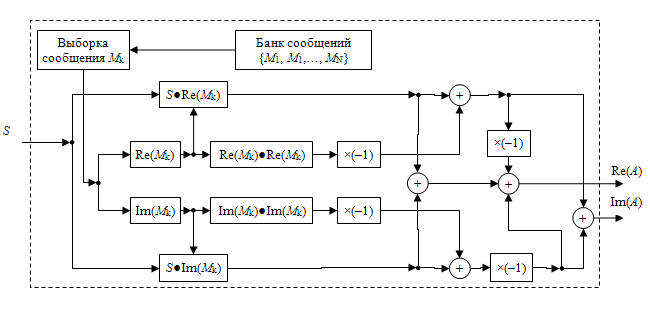
Рисунок 1. Блок-схема реализации метода разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов

 

Рассмотрим подробнее порядок преобразований, приведённый на схеме (рис. 1). Из банка сообщений {M₁, M₁,…, M_N} выбирается некоторое сообщение M_k (где k = 1, 2, …, N), далее сообщение разделяется на вещественную Re(M_k) и мнимую  Im(M_k) составляющие, после чего вычисляется корреляционные функции:

S●Re(M_k) содержащая в себе аналоги корреляции комплексных сигналов Re(S)●Re(M_k)+Im(S)●Re(M_k);

и S●Im(M_k) содержащая в себе аналоги корреляции комплексных сигналов Re(S)●Im(M_k)+Im(S)●Im(M_k), причём слагаемое (Im(S)●Im(M_k)) с плюсом, из-за фактического отсутствия множителя квадрата мнимой единицы j². Одновременно вычисляются корреляции с последующим умножением на минус единицу (–1)×Re(M_k)●Re(M_k) и (–1)×Im(M_k)●Im(M_k), соответственно. Последующее сложение:

 S●Re(M_k)+(–1)×Re(M_k)●Re(M_k)=                                                                   

=Re(S)●Re(M_k)+Im(S)●Re(M_k)–Re(M_k)●Re(M_k)=Im(S)●Re(M_k)    (8)

и

S●Im(M_k)+(–1)×Im(M_k)●Im(M_k)=                                                                    

=Re(S)●Im(M_k)+Im(S)●Im(M_k)–Im(M_k)●Im(M_k)=Re(S)●Im(M_k),   (9)

позволяет выделить элементы мнимой составляющей АКФ. Отметим, что последние знаки равенства в выражениях (8), (9) допустимы, если сигнал S является искомым сообщением M_k. Причём за счёт комплексной сопряжённости (2) элемент мнимой части Re(S)Im(M_k) в окончательном выражении для мнимой части Im(A) будет с минусом:

Im(A)=Im(S)●Re(M_k)–Re(S)●Im(M_k).                                              (10)

Таким образом, вычислена мнимая часть АКФ Im(A).

Подобные рассуждения позволяют построить схему вычисления вещественной части, которая, с практической точки зрения, для распознавания сообщения наиболее интересна, т.к. центральный элемент АКФ является вещественным. Используя ранее полученные корреляционные функции S●Re(M_k)=Re(S)●Re(M_k)+Im(S)●Re(M_k) и S●Im(M_k)=Re(S)●Im(M_k)+Im(S)●Im(M_k), вычислим разности с, так же полученными ранее, корреляционными функциями Im(S)●Re(M_k) и Re(S)●Im(M_k), что возможно записать как:

S●Re(M_k)+S●Im(M_k)–Im(S)●Re(M_k)–Re(S)●Im(M_k)=                                      

=Re(S)●Re(M_k)+Im(S)●Re(M_k)+Re(S)●Im(M_k)+Im(S)●Im(M_k)–Im(S)●Re(M_k)–        

–Re(S)●Im(M_k)=Re(A).                                                                    (11)

Таким образом, на выходе преобразователя получим мнимую Im(A) и вещественную Re(A) составляющие искомой АКФ.

В силу линейности всех рассмотренных преобразований, подавая на вход преобразователя в качестве сигнала S единичную функцию δ, для различных сообщений M_к, выбранных из банка сообщений {M₁, M₁,…, M_N}, возможно построить банк сверточных функций для распознавания сообщений, причём реализация может быть выполнена полностью на аппаратной основе [10], что обеспечит работу приёмника в режиме реального времени.

Практическая реализация и апробация метода

Для практического тестирования и исследования предложенного метода разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов была разработана программа MatLab [11], [12]. В качестве матрицы для формирования широкополосного сигнала использовалась матрица размером 4×3, из класса MC₉ с особой формой АКФ [2]:

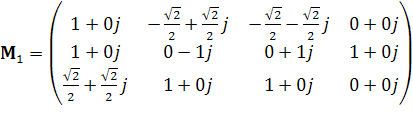,                       (12)

Для матрицы M₁, матрица АКФ (1), имеет следующий вид (не целые значения элементов матрицы записаны с округлением):

.

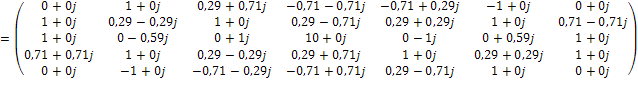Матрица, определяющая широкополосное сообщение M₁(t), будет иметь вид:

.

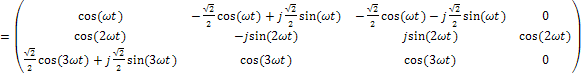На изображении (рис. 2) представлены вещественная Re(M₁[n])  и мнимая Im(M₁[n]) составляющие сообщения M₁[n], полученные в цифровом виде средствами MatLab, где n – номера отсчётов, т.е. цифровой эквивалент времени t в аналоговом представлении сообщения M₁(t).

 

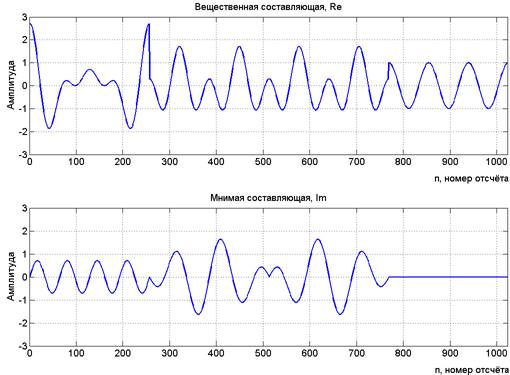
Рисунок 2. Вещественная Re(M_k[n])  и мнимая Im(M_k[n]) составляющие сообщения M_k[n]

 

Выполнение операций, в соответствии с методом разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов, позволяет получить следующие результаты: на изображении (рис. 3) два графика слева получены в результате работы предложенного метода, два графика справа получены в результате расчёта обычной АКФ сообщения M₁[n] с комплексными значениями и последующего разделения АКФ на вещественную и мнимую части.

 

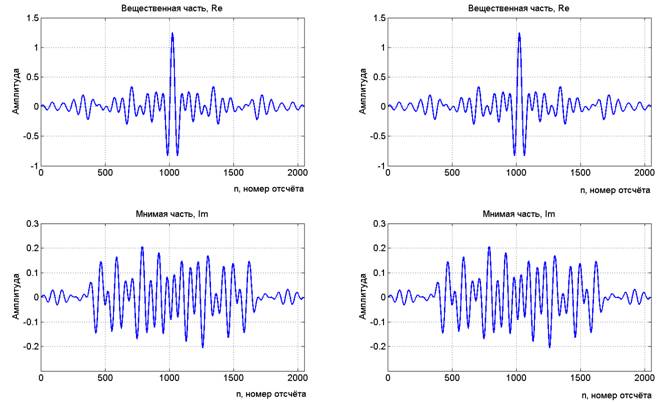
Рисунок 3. Слева - результаты работы предложенного метода, справа -результаты расчёта обычной АКФ сообщения M₁[n] с комплексными значениями и последующего разделения АКФ на вещественную и мнимую части, все графики нормированы с помощью деления на число отсчётов исходного сообщения M₁[n]

 

Очевидно, что графики совпадают, результаты численного сравнения, полученные как нахождение максимального элемента при вычислении поэлементной разности простой АКФ и результатов применения метода разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов, показывают, что абсолютное значение максимального расхождения значений , что является следствием погрешностей [12] при вычислениях с плавающей точкой (формат double MatLab).

Дополнительно рассмотрим примеры сравнения вычисления корреляционных функций: (рис. 4 а.) – вещественная часть, полученная с помощью предложенного метода; (рис. 4 б.) – вещественная часть, вычисления корреляционной функции входного сообщения с комплекснозначным сообщением M₁[n] из банка (рис. 1); (рис. 4 в.) –  вычисление корреляционной функции входного сообщения с только вещественной частью сообщения M₁[n] из банка.

 

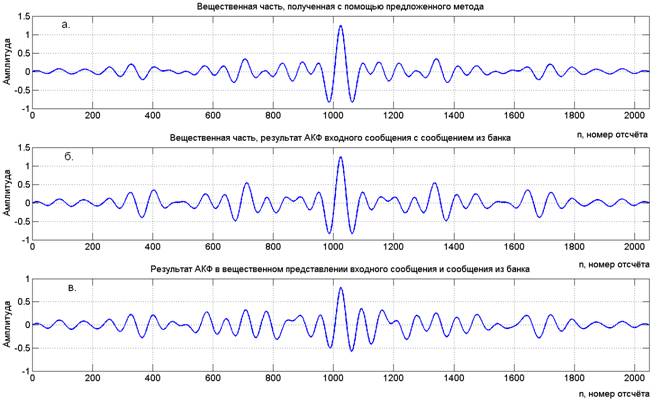
Рисунок 4. Сравнение вычисления корреляционных функций различными способами

 

Сравнение графиков (рис. 4) позволяет сделать вывод о том, что наилучший результат по критерию максимальное значение центрального элемента АКФ при минимальном значении лепестков позволяет получить предлагаемый метод.

Заключение

Произведена разработка и исследование метода разделения во времени автокорреляционных гармонических составляющих широкополосных сигналов. Предложенный метод позволяет эффективно разделять на вещественную и мнимую автокорреляционные составляющие распознаваемых сообщений, при распознавании имеется возможность использовать весь частотно-временной ансамбль сообщения, а следовательно использовать все преимущества сигналов, сформированных на основе матриц с АКФ специального вида, имеющих комплексные значения элементов.

Отметим достоинства метода:

– нет необходимости частотного разделения сигнала, что позволяет снизить искажения формы сигнала в трактах приёмного устройства;

– использование всего множества элементов широкополосного сигнала, т.е. на составляющие разделяется не сигнал, а его АКФ, что позволяет эффективно распознавать сигналы, скрытые в шуме;

– простота и возможность реализации в режиме реального времени.

 

Литература

1.            Ипатов В. Широкополосные системы и кодовое разделение сигналов. Принципы и приложения. М.: Техносфера, 2007. – 488 с.

2.            Гришенцев А. Ю., Коробейников А. Г.  Алгоритм поиска, некоторые свойства и применение матриц с комплексными значениями элементов для стеганографии и синтеза широкополосных сигналов // Журнал радиоэлектроники [электронный журнал]. 2016, № 5, URL: http://jre.cplire.ru/jre/may16/11/text.pdf

3.            Гришенцев А. Ю., Коробейников А. Г. Понижение размерности пространства при корреляции и свертке цифровых сигналов  // Изв. вузов. Приборостроение. 2016. Т. 59, № 3. С. 211—218. DOI 10.17586/0021-3454-2016-59-3-211-218

4.            Гришенцев А. Ю., Коробейников А. Г., Величко Е. Н., Непомнящая Э. К., Розов С. В. Синтез бинарных матриц для формирования сигналов широкополосной связи  // Радиотехника, 2015, №9, С.: 51– 58.

5.            Дятлов А. П., Кульбикаян Б. Х. Корреляционная обработка широкополосных сигналов в автоматизированных комплексах радиомониторинга  // М.: Горячая линия–Телеком, 2014. – 332 с.: ил.

6.            Арслан Х., Чен Чж. Н., Бендетто М. Сверхширокополосная беспроводная связь // М.: Техносфера, 2012 – 640 с.: ил.

7.            Яманов Д. Н., Жаворонков С. С. Динамическое поляризационное разделение каналов // Научный вестник МГТУ ГА, 2006, № 98(2), С.: 13 – 17.

8.            Родимов А. П., Поповский В. В. Статистическая теория поляризационно-временной обработки сигналов и помех // М.: Радио и связь, 1984. – 272 с.:ил.

9.            Бобков В., Ефимов М., Киселёв А. Поляризационное уплотнение – перспективы внедрения Использование поляризационного разделения сигналов в системах спутниковой связи России // Connect [электронный ресурс],  №4 (2004), C.: 120 – 123.

URL: http://www.connect.ru/article.asp?id=4547

10.       Герасимов И. В., Сафьянников Н. М., Якимовский Д. О. Сложно-функциональные блоки смешанных систем на кристалле: автоматизация функционального проектирования: монография под ред. И. В. Герасимова. – СПб.: Изд-во «ЭЛМОР», 2012. – 237 с.

11.       Солонина А. И., Клионский Д. М., Меркучева Т. В., Петров С. Н. Цифровая обработка сигналов и MatLab: учебное пособие // СПб.: БХВ-Петербург, 2014. – 512 с.:ил.

12.       Гришенцев А. Ю., Коробейников А. Г. Методы и модели цифровой обработки изображений: монография. СПб: Изд-во Политехн. ун-та, 2014. – 190 с.: ил.