УДК 621.391
Обнаружение ошибок кодом БЧХ над полем GF(4) на основе СПЕКТРАЛЬНОГО ОПИСАНИЯ
В. А. Вершинин
Рыбинский государственный авиационный технический университет им. П. А. Соловьева
Статья поступила в редакцию 6 сентября 2016 г.
Аннотация. В статье рассматривается спектральное описание кода БЧХ над полем GF(4). Цель кодирования – обнаружение ошибок. Произведена оценка эффективности кодирования, когда число ошибок в кодовом слове больше числа гарантированно обнаруживаемых ошибок.
Моделирование процесса декодирования показало, что наибольшее значение вероятности необнаруженной ошибки получается, когда число ошибок в кодовом слове равно кодовому расстоянию. Эта вероятность используется в статье для оценки сверху вероятности необнаруженной ошибки.
Если число ошибок в кодовом слове больше или равно кодовому расстоянию, то при увеличении длины кодового слова и неизменной величине кодового расстояния можно получить приемлемое значение вероятности необнаруженной ошибки.
Ключевые слова: спектральное описание, обнаружение ошибок, код БЧХ.
Abstract. The article discusses the spectral description of BCH code over the field GF(4). The purpose of the coding – error detection. The assessment of coding efficiency, when the number of errors in the code word greater than the number of guaranteed detectable errors.
Simulation of the decoding process showed that the highest value of the probability of undetected error is obtained when the number of errors in the code word equal to the code distance. This probability is used in the article to estimate from above the probability of undetected error.
If the number of errors in the code word is greater than or equal to the code distance, then increase the length of the code words in the constant value of the code distance it is possible to obtain an acceptable value of probability of undetected error.
Key words: spectral description, error detection, BCH code.
1. Введение
Описать код БЧХ можно [1],
исходя из спектрального описания кода Рида-Соломона на основе дискретного
преобразования Фурье (ДПФ). Опишем код Рида-Соломона, используя ДПФ над полем
, где 
.
Элемент i-ой строки и j-го столбца матрицы 
прямого ДПФ равен 
,
а такой же элемент матрицы 
обратного ДПФ равен 
; 
; 
. Здесь α – примитивный элемент поля , 
. Для примера, при 
и
, используя пакет Matlab, можно получить:
ДПФ
используется для спектрального описания кода Рида-Соломона следующим образом. Пусть
блоку элементов сообщения длиной 
соответствует вектор 
, у которого 
последовательных
элементов являются нулевыми и называются проверочными, а остальные равны элементам
сообщения и называются информационными. Кодовый вектор 
получается с помощью матрицы обратного
ДПФ:
Элементы сообщения и вектора c могут принимать значения 
. Такой код называется кодом Рида-Соломона,
его кодовое расстояние 
. При декодировании используется матрица прямого ДПФ.
Перейдем к описанию кода БЧХ над полем 
. Для этого будем использовать код Рида-Соломона над полем 
при 
. Пусть блоку элементов сообщения длиной k
соответствует вектор 
, элементы которого могут
принимать 4 значения (нулевое значение и значения элементов поля , порядок которых делит 
). По определенному алгоритму образуется
вектор так, чтобы элементы кодового вектора принимали
те же 4 значения.
Для осуществления указанного алгоритма вектор b разбивается на
группы. Каждая группа состоит из свободных и связанных элементов. Индексы связанных
элементов получаются умножением по модулю n
индексов свободных элементов на 
. Если группа состоит
из r элементов, то свободный элемент группы может
принимать 
значений (нулевое значение и значения
элементов поля , порядок которых делит 
). Связанные элементы группы принимают
значения, равные степени свободного элемента
этой группы. При кодировании r элементов
вектора a линейно
преобразуются в свободный элемент вектора b. Кодовый вектор
формируется согласно (1) путем обратного ДПФ вектора b.
Сказанное выше поясняется таблицей 1 для .
Таблица 1
|
Номер группы |
Свободные элементы |
Связанные элементы |
Получение связанных элементов |
Значения свободных элементов |
Получение свободных элементов |
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
5 |
|
|
|
|
|
|
6 |
|
|
|
|
|
|
7 |
|
|
|
|
|
|
8 |
|
|
|
|
|
|
9 |
|
|
|
|
|
Здесь элементы вектора a и c могут принимать 4 значения: 0, 1, 6 и 7.
2. Спектральное описание кода БЧХ
Базируясь на изложенном выше описании кода БЧХ, автором
предлагается [2], получить матрицу 
прямого и матрицу 
обратного преобразования над полем .
Матрица получается построчно
следующим образом. Формируется вектор 
и по формуле (1) определяется значение вектора c, которое и является значением 0-й строки
матрицы при замене значений элементов поля на значения элементов поля . Затем формируется вектор 
и по формуле (1) получается 1-я строка матрицы
и так далее. Последняя строка получается с
помощью вектора 
. Матрица получается как обратная матрице .
Для можно получить:
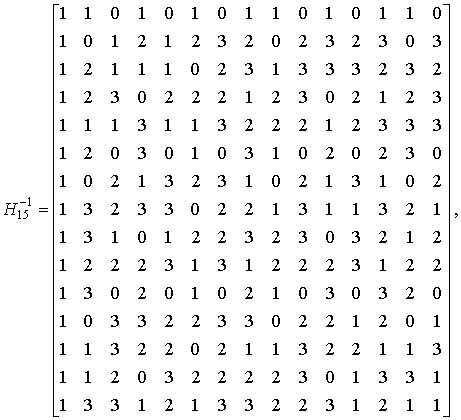
При получении этих матриц
значения 0, 1, 6 и 7 элементов поля 
заменялись
значениями 0, 1, 2 и 3 элементов поля .
3. Кодирование
Пусть блоку элементов сообщения длиной k
соответствует вектор , элементы которого могут
принимать значения 0, 1, 2, 3. При этом последовательных
элементов этого вектора принимаются равными нулю и называются проверочными, а остальные k равны элементам сообщения и называются
информационными. От значения зависит кодовое расстояние d
кода БЧХ. Величину d принято
оценивать конструктивным кодовым расстоянием 
. При
этом 
, а значение 
равно
количеству последовательно расположенных нулевых элементов вектора b , которые получаются
при преобразовании проверочных элементов вектора a.
Кодовый вектор получается путем обратного преобразования над
полем :
При этом
элементы вектора a задаются,
а элементы вектора c получаются над полем .
В таблице 1 приведены параметры некоторых кодов БЧХ,
имеющих 
.
Таблица 2
|
Код (n, k) |
Проверочные элементы вектора a |
Нулевые элементы вектора b, получающиеся из проверочных элементам вектора a |
|
(15,8) |
|
|
|
(63,53) |
|
|
|
(255,242) |
|
|
4. Декодирование с обнаружением ошибок
Пусть кодовому слову на входе декодера соответствует вектор
, (3)
где e – вектор ошибок. Этот вектор
связан с наличием помех в канале связи. Если в результате действия помех
искажаются элементы кодового слова, то соответствующие элементы вектора ошибок
принимают значение 1, 2 или 3. Неискаженным элементам кодового слова
соответствуют нулевые элементы вектора ошибок. В декодере осуществляется прямое
преобразование вектора c', в результате получается вектор 
. Учитывая (2),
.
(4)
Очевидно, что при отсутствии ошибок 
и 
.
Обнаружение ошибок в кодовом слове осуществляется путем контроля значений
проверочных элементов вектора 
. Если хотя бы один из
проверочных элементов не равен нулю, то это соответствует обнаружению ошибок.
Гарантировано обнаруживаются ошибки, если их количество в кодовом слове не
превышает 
. Если число ошибок больше , то ошибки могут быть не обнаружены с определенной
вероятностью. Оценка этой вероятности является целью данной работы.
5. Вероятность необнаруженной ошибки
Будем оценивать вероятность необнаруженной ошибки при
фиксированном числе r ненулевых
элементов вектора ошибок. При этом предполагаем, что все возможные варианты
размещения ненулевых элементов равновероятны и каждый из этих элементов с
равной вероятностью принимает значение 1, 2, 3. Очевидно, что вероятность
необнаруженной ошибки равна нулю при 
.
Моделирование процесса декодирования показало, что
наибольшее значение вероятности необнаруженной ошибки получается при 
. Именно эту вероятность P
будем использовать для оценки сверху вероятности необнаруженной ошибки при
фиксированном значении r.
Образуем матрицу g, состоящую
из столбцов матрицы 
с номерами проверочных элементов.
Таким образом, матрица g имеет n
строк и столбцов. Любые строки
матрицы g, соответствующие ненулевым элементам вектора e,
являются линейно независимыми. Тогда при произведение
и такие ошибки всегда обнаруживаются. При
, для определенных размещений ненулевых
элементов вектора e и
определенных значений этих элементов возможно 
, что
соответствует необнаруженным ошибкам.
Пусть u – число линейно независимых строк матрицы g,
соответствующих ненулевым элементам вектора e, значение
u может быть , либо d.
Очевидно, что вероятность размещения 
, при котором возможно равна вероятности значения 
. Вероятность ненулевых значений элементов
вектора e при
условии , для которых равна 
. Выражение для 
получено
из следующих соображений. Число возможных комбинаций ненулевых значений
элементов вектора e равно 
, из них 3 (при
условии ) приводят к . Тогда
.
(5)
Вероятность 
определяется путем
проведения N испытаний при случайно формируемых размещениях d
ненулевых элементов в векторе ошибок с использованием пакета Matlab.
При каждом испытании определяется ранг матрицы, которая получается из матрицы g
путем исключения из нее строк, соответствующих нулевым элементам вектора e.
При этом определяется число испытаний 
с
рангом, равным . Затем с помощью функции binofit(N1,N) пакета Matlab получаем точечную оценку 
значения
, нижнюю 
и верхнюю
границу оценки с доверительной
вероятностью 0.95.
Далее на основании (5) можно определить 
, 
, 
, используя 
, и соответственно.
Результаты, полученные указанным путем, для кодов с
помещены в таблице 3, а для кодов с 
– в таблице 4.
Таблица 3
|
Код (n,k) |
(15,8) |
(63,53) |
(255,242) |
|
N |
|
|
|
|
|
20925 |
399 |
99 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 4
|
Код (n,k) |
(15,7) |
(63,50) |
(255,238) |
|
N |
|
|
|
|
|
20934 |
21 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6. Выводы
Предлагаемое спектральное
описание кода БЧХ позволяет осуществлять кодирование и декодирование над полем , что ускоряет эти процессы.
Если число ошибок в
кодовом слове больше , то с ростом длины кодового слова n и постоянном значении d вероятность необнаруженной ошибки
уменьшается и при достаточно большом n можно получить приемлемое значение этой вероятности.
С увеличением n при постоянном значении d увеличивается скорость кода 
, что также является положительным
фактом.
С увеличением d при постоянном значении n вероятность необнаруженной ошибки уменьшается.
Литература
1. Блейхут Р. Теория и практика кодов, контролирующих ошибки. Пер. с англ.– М.: Мир, 1986.– 576 с.
2. Передача дискретных сообщений/ Вершинин В.А. Рыбинская государственная авиационная технологическая академия им. П.А. Соловьева. Рыбинск, 2002.– 82 с.– Деп. в ВИНИТИ 17.12.2002 г., № 2196-В2002