УДК 535.36, 621.396.11
Экспериментальные спектры ослабления, рассеяния и поглощения миллиметровых волн в сухом свежевыпавшем снеге
В. А. Голунов1, А. В. Кузьмин2, Д. П. Скулачев2, Г. И. Хохлов1
1 Институт радиотехники и электроники им. В. А. Котельникова РАН
(Фрязинский филиал)
2 Институт космических исследований РАН
Статья поступила в редакцию 24 августа 2016 г.
Аннотация. На частотах 37,5, 60 и 94ГГц выполнены измерения полных коэффициентов отражения, пропускания и коэффициента пропускания когерентной интенсивности в зависимости от толщины слоя сухого свежевыпавшего снега с различными структурами. Экспериментальные характеристики аппроксимированы с использованием модели FIRE. Проанализированы экспериментальные частотные зависимости коэффициента экстинкции и модельных величин: коэффициентов поглощения, рассеяния и ослабления некогерентного излучения. Установлено, что сильное влияние на рассеяние и ослабление миллиметровых волн в сухом свежевыпавшем снеге могут оказывать кластеры частиц, вследствие чего частотные зависимости коэффициентов ослабления и рассеяния значительно отличаются от теоретических, рассчитанных в приближении теории сильных флуктуаций.
Ключевые слова: рассеяние, ослабление, миллиметровые волны, снежный покров, частотная зависимость, кластеры.
Abstract: The reflectivity, transmissivity and coherent intensity transmittance depending on the thickness of the layer of dry fresh snow with different structures are measured at frequencies 37.5, 60 and 94GHz. Experimental data are approximated using FIRE model. The experimental frequency dependence of the extinction coefficient and the model variables such as the absorption and scattering coefficients and attenuation of incoherent radiation are analyzed. It was found that clusters of particles can strongly influence upon the scattering and attenuation of millimeter waves into dry fresh snow. Due to the clusters scattering the frequency dependence of attenuation and scattering coefficients are significantly different from the theoretical ones determined by the theory of strong fluctuations.
Key words: scattering, attenuation, millimeter waves, fresh snow, frequency dependence, clusters.
Введение
Свежевыпавший снег, образуя верхний слой снежного покрова, определяет граничные условия для распространения и излучения электромагнитных волн. В связи с этим характеристики ослабления, рассеяния и поглощения электромагнитных волн в свежевыпавшем снеге, как правило, востребованы при решении различных задач активного и пассивного зондирования земной поверхности. Вышеперечисленные характеристики практически не исследованы в диапазоне миллиметровых волн.
В данной работе рассматривается только сухой (т.е. не тающий) снег. Встречается несколько разновидностей сухого свежевыпавшего снега: пушистый и порошковидный, которые выпадают при температурах, близких 00С, игольчатый - при температурах ниже -150С, и снег-изморозь – осаждение разветвленных кристаллов из парообразной формы на холодную снежную поверхность [1]. Вследствие различных метеоусловий выпадения осадков свежевыпавший снег может иметь значения плотности в широком интервале: 0,01…0,39 г/см3,- при этом снег тем плотнее, чем выше температура воздуха и сильнее ветер [1]. В данной работе исследовался свежевыпавший снег в условиях аномально теплой зимы 2016г., когда дневные значения температуры воздуха преимущественно составляли 0…50С, а ночные редко опускались ниже -100С. Как правило, осадки выпадали в виде пушистого снега при положительной температуре воздуха, а возможность для измерения его радиофизических характеристик предоставлялась по погодным условиям через 2…5 суток после выпадения снега.
Сухой снежный покров, являющийся смесью кристаллов льда и воздуха, рассматривается либо как плотная случайная дискретная среда, либо как сплошная случайная среда [2]. К настоящему времени пока не разработана строгая теория, позволяющая рассчитывать характеристики рассеяния и излучения при произвольных параметрах указанных сред. Из существующих строгих теорий выделим теорию сильных флуктуаций [3,4], которая допускает возможность ее применения к сухому свежевыпавшему снегу в диапазоне миллиметровых волн [5].
Цель работы – экспериментально изучить частотные зависимости ослабления, рассеяния и поглощения миллиметровых волн в сухом свежевыпавшем снеге. Исследования выполнены на частотах 37,5; 60 и 94 ГГц.
Основным способом экспериментального исследования характеристик излучения однородного снега является измерение интенсивности теплового излучения однородного слоя как функции его толщины. Слой с заданной толщиной формируется из образцов однородного снега, аккуратно изъятых из востребованного слоя снежного покрова с самосформировавшейся структурой. Образцы снега при этом могут помещаться последовательно на плоский металл и поверхность черного тела в полевых условиях [6], или, как в данной работе, в цилиндрические контейнеры для последующих измерений в охлажденном помещении.
В случае рассевающих сред надежно измерить можно полные коэффициенты отражения и пропускания, а также коэффициент пропускания когерентной интенсивности. Для таких величин, как коэффициенты поглощения, обратного и прямого рассеяния единичного слоя, могут быть получены только оценки по результатам измерения указанных выше первичных величин с применением тех или иных моделей излучения рассеивающего слоя. Вследствие этого особое внимание в данной работе уделяется выбору модели, наиболее адекватно описывающей закономерности поглощения и рассеяния в сухом снеге и снегоподобных средах.
1. Аппаратура и методика измерений
Измерения выполнены на частотах 37,5; 60 и 94 ГГц с использованием радиометрического стенда и методики, описанных в [7]. В стенде использовалась искусственная «холодная» подсветка исследуемых образцов, что позволило измерять характеристики ослабления и излучения снега на частоте 60ГГц (в полевых условиях это невозможно вследствие резонансного поглощения молекулярным кислородом в атмосфере). Для каждой исследованной структуры снега измерялись три величины: полные коэффициенты отражения R, пропускания t и коэффициент пропускания когерентной интенсивности tк как функции толщины слоя. Коэффициент пропускания когерентной интенсивности tк измерялся при этом с усреднением в угловом интервале 110.
Образцы самосформировавшихся структур снега аккуратно (т.е. без нарушения структур) изымались из выбранного слоя снежного покрова, укладывались друг на друга до достижения требуемой толщины, после чего путем «ввинчивания» измерительных цилиндрических металлических контейнеров диаметром 0,2м в их толщу оказывались внутри этих контейнеров. Исследованы 5 видов структур снега, параметры которых приведены в таблице 1.
Таблица 1.
|
№ струк-туры |
дата |
параметры снежных структур |
||||
|
возраст |
ρV |
d, мм |
t0C |
примечание |
||
|
1 |
21.01.16г. |
Односуточный, игольчатый |
0,25 |
< 0,5 |
-10 |
замерзшие капли выпавшего кратковременного дождя |
|
2 |
21.02.16г. |
месячный |
0,20 |
<1 |
-2…-3 |
первый слой ниже свежевыпавшего снега |
|
3 |
25.02.16г. |
Пятисуточный |
0,20 |
< 0,5 |
-3…-5 |
выпавший снег находился в условиях дневной оттепели преимущественно при сплошной облачности |
|
4 |
01.03.16г. |
Трехсуточный |
0,3…0,34 |
< 0,5 |
-4…-6 |
структура снега преднамеренно разрушена |
|
5 |
15.03.16г. |
|
0,45…0,5 |
< 1 |
-4…-6 |
снег, просеянный через сетку с ячейками 1мм |
Из-за аномально теплой зимы удалось исследовать только одну структуру свежевыпавшего снега (структура 1), не подвергавшейся влиянию положительной температуры атмосферы. Кроме самосформировавшихся структур 1, 3 свежевыпавшего снега в целях сравнения дополнительно исследованы три вида структур, одна из которых (структура 2) – мелкозернистый снег, находившийся под слоем свежевыпавшего снега, другая - структура 4 - это разрушенная путем перемешивания тоненькой палочкой структура 3, и еще одна – структура 5 - мелкозернистый снег (размеры частиц меньше 1мм), выделенный из зернистого снега путем фильтрации через сетку с ячейками 1мм.
2. Модели излучения снега
При разработке алгоритма восстановления высоты снежного покрова на основе данных пассивного дистанционного зондирования требуются обоснованный выбор модели излучения сухого снежного покрова и адекватные спектральные зависимости модельных величин. К настоящему времени разработаны и применяются следующие модели излучения снежного покрова: двухпотоковая теория Кубелки-Мунка [8], FIRE (FIRE - аббревиатура Fryazino Institute of Radioengineering and Electronics) [9], MEMLS (Microwave Emission Model of Layered Snowpacks) [10] и HUT (Helsinki University of Technology) [11].
Модель HUT, как утверждают авторы, применима, когда в среде существенно доминирует интенсивность рассеяния вперед. Следовательно, ее применимость ограничивается средами, размеры дискретных частиц в которых существенно превосходят длину волны.
Модель MEMLS разработана для расчета яркостной температуры слоистого снежного покрова, но в случае однослойного покрова она сводится к двухпотоковой теории Кубелки-Мунка. Модели FIRE и Кубелки-Мунка имеют крайне слабые количественные взаимные расхождения при расчете полных коэффициентов отражения и пропускания сухого снега при одних и тех же значениях исходных параметров (коэффициентов поглощения и рассеяния) [12]. В отличие от двухпотоковой теории Кубелки-Мунка модель FIRE учитывает влияние когерентной интенсивности. В связи с этим дальнейшее рассмотрение экспериментальных данных будет основываться на применении модели FIRE.
В соответствии с моделью FIRE полные коэффициенты отражения R и пропускания t слоя снега толщиной h записываются в виде:
, (1)
,
(2)
где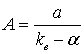 
, 
, 
-
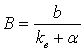коэффициент ослабления некогерентного излучения, 
- коэффициент экстинкции, ka
– коэффициент поглощения, a
и b – коэффициенты
рассеяния вперед и назад соответственно [9].
Как следует из соотношений (1)-(2), модель FIRE позволяет осуществлять оценку погонных коэффициентов ka, а и b, если совместно с R и t измеряется коэффициент пропускания когерентной интенсивности, определяемый в виде:
(3)
Модель FIRE позволяет с удовлетворительной точностью аппроксимировать зависимости R(h) и t(h), рассчитанные в результате численного решения уравнения переноса излучения [9].
3. Результаты исследования
Для теплового излучения каждой структуры снега измерялись три характеристики: полные коэффициенты отражения R, пропускания t и коэффициент пропускания когерентной интенсивности tк как функции толщины слоя снега. Затем экспериментальные данные аппроксимировались соответствующими соотношениями модели FIRE. В результате аппроксимации определялись анализируемые в дальнейшем значения модельных коэффициентов ke, ka, b и R0.
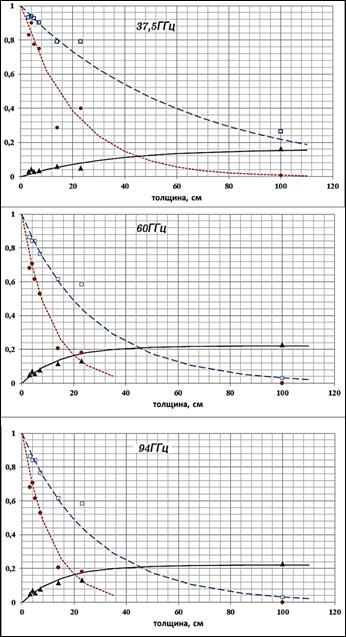
Рис.1.
Графики экспериментальных (символы) и аппроксимационных (линии)
зависимостей
полных коэффициентов отражения R
(черный цвет),
пропускания t
(синий цвет) и коэффициента пропускания когерентной интенсивности tк
(красный цвет) от толщины слоя сухого снежного покрова (структура 3).
Для примера на рис.1а,б,в показаны графики экспериментальных и модельных зависимостей полных коэффициентов отражения, пропускания и коэффициента пропускания когерентной интенсивности от толщины слоя структуры 3 свежевыпавшего снега для трех частот: 37,5; 60 и 94 ГГц. Заметные отклонения экспериментальных значений от аппроксимационных графиков, наблюдаемые при значениях толщины 14 и 24см, обусловлены неоднородностями структуры снега. Они проявляются похожим образом на всех трех частотах.
В таблице 2 приведены значения модельных параметров R0, ka, α и ke, определенные для всех исследованных структур снега в результате аппроксимации экспериментальных зависимостей R(h), t(h) и tk(h) с использованием модели FIRE.
Таблица 2.
|
№ структуры снега |
f, ГГц |
|||||||||
|
37,5 |
60 |
94 |
37,5 |
60 |
94 |
37,5 |
60 |
94 |
||
|
R0 |
ka, см-1 |
b, см-1 |
||||||||
|
1 |
0,17 |
0,15 |
0,22 |
0,0039 |
0,013 |
0,052 |
0,0019 |
0,0052 |
0,033 |
|
|
2 |
0,28 |
0,35 |
0,355 |
0,013 |
0,025 |
0,074 |
0,013 |
0,037 |
0,114 |
|
|
3 |
0,15 |
0,16 |
0,2 |
0,004 |
0,011 |
0,022 |
0,0017 |
0,0049 |
0,015 |
|
|
4 |
0,08 |
0,14 |
0,2 |
0,0047 |
0,013 |
0,036 |
0,0029 |
0,0082 |
0,031 |
|
|
5 |
0,15 |
0,24 |
0,28 |
0,0089 |
0,031 |
0,110 |
0,0037 |
0,0248 |
0,115 |
|
|
|
α, см-1 |
ke, см-1 |
|
|||||||
|
1 |
0,0055 |
0,017 |
0,08 |
0,021 |
0,037 |
0,24 |
||||
|
2 |
0,023 |
0,05 |
0,15 |
0,09 |
0,16 |
0,45 |
||||
|
3 |
0,0057 |
0,015 |
0,034 |
0,03 |
0,048 |
0,09 |
||||
|
4 |
0,007 |
0,020 |
0,060 |
0,018 |
0,040 |
0,132 |
||||
|
5 |
0,012 |
0,05 |
0,195 |
0,025 |
0,10 |
0,38 |
||||
Для исследованных структур на рисунке 2 показаны графики экспериментальных зависимостей коэффициента полного отражения полубесконечного слоя. Видно, что наиболее сильно отражают структуры 2 (мелкозернистый снег) и 5 (снег, просеянный через сетку с ячейками 1мм).
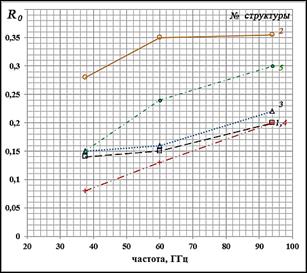
Рис.2. Экспериментальные спектры коэффициента
полного отражения
исследованных структур:
.
То, что коэффициенты отражения других структур, относящихся к свежевыпавшему снегу, на частотах 60 и 94 ГГц заметно ниже, является ожидаемым эффектом, поскольку интенсивность рассеяния в сухом снеге тем выше, чем крупнее кристаллы [13]. Однако, как следует из рассматриваемых графиков, эта закономерность нарушается на частоте 37,5 ГГц. Видно, что на этой частоте значения коэффициента полного отражения, во-первых, практически одинаковы для трех структур: мелкозернистой 2 и свежевыпавшего снега 3, 1, - во-вторых, незначительно отличаются от таковых для структур 3, 1 на частоте 60 ГГц. Это может означать, что излучение на частоте 37,5 ГГц рассеивается в свежевыпавшем снеге на неоднородностях, размеры которых больше, чем при рассеянии на более высоких частотах. Такими неоднородностями в свежевыпавшем снеге могут быть только кластеры. Действительно, частицы льда, из которых формируется структура снега, вследствие своей контактности (или «липкости»), образуют каркасную систему, которая обеспечивает определенную жесткость структуры. Очевидно, что в зависимости от объемной плотности снега перемычки каркаса могут состоять из двух и более ледяных частиц. Именно такие группы коррелированных частиц принято называть кластерами.
Влияние кластеров на интенсивность рассеяния определяется как соотношением их размера и длины волны, так и соотношением размера частиц и длины волны. Известно [14], что при увеличении размера диэлектрических частиц коэффициент экстинкции на фиксированной длине волны стремится к некоторому предельному значению. Аналогичная зависимость имеет место как в случае кластеров [15], так и снегоподобных сред [13]. Следовательно, кластеры могут оказывать доминирующее влияние на рассеяние только при размерах частиц, заметно меньших длины волны. В других случаях их влияние значительно слабее, главным образом, потому, что количество кластеров заметно меньше, чем количество частиц. При этом следует иметь в виду, что кластеры в силу их относительно большого размера рассеивают падающее когерентное поле преимущественно вперед. Это означает, что влияние кластеров связано, главным образом, с ослаблением когерентной интенсивности.
Рассмотрим теперь частотные характеристики других модельных величин. Для аппроксимации их частотных зависимостей использовалась функция вида:
(4)
где f выражена в ГГц, q=(b, ke, ke, α,), рq и η – некоторые эмпирические параметры, зависящие не только от модельных величин, но и от структуры снега. Для более целенаправленного подбора показателя степени η осуществлялась предварительная оценка его значения на основе соотношения, следующего из (4):
(5)
Оценочные значения η для всех исследуемых модельных величин представлены в таблице 3.
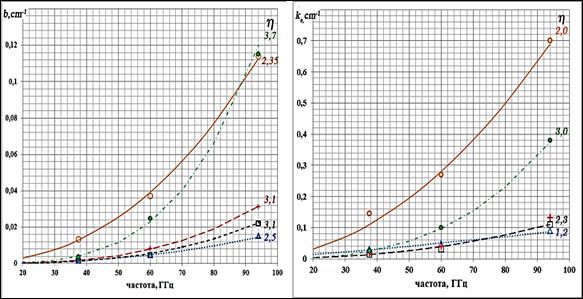
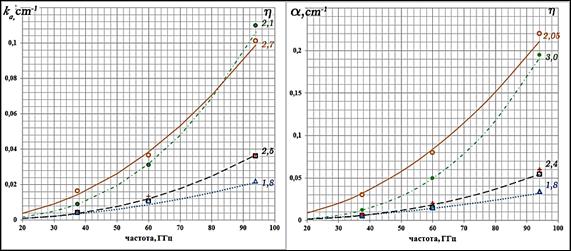
Графики экспериментальных и аппроксимационных зависимостей коэффициентов обратного рассеяния b, экстинкции ke, ослабления некогерентного излучения α и поглощения ka для всех структур показаны соответственно на рис.3а,б,в,г, апроксимационные значения параметров η /pq приведены в таблице 4. Из представленных графиков следует, что все рассматриваемые структуры в соответствии со значениями модельных величин разделяются так же, как и в рассмотренном выше случае, на две группы: структуры свежевыпавшего снега 1, 3, 4 и мелкозернистые структуры 2, 5. Точность аппроксимации частотной зависимости модельных величин соотношением (4) характеризуется шириной интервала, в котором заключены значения показателя степени в каждом столбце таблицы 3: чем уже интервал, тем точнее аппроксимация.
Таблица 3.
|
модельная величина |
f1/f2 |
номер структуры |
||||
|
1 |
2 |
3 |
4 |
5 |
||
|
b |
37/60 |
2,13 |
2,19 |
2,24 |
2,22 |
4,07 |
|
37/94 |
3,11 |
2,34 |
2,39 |
2,97 |
3,75 |
|
|
60/94 |
4,13 |
2,50 |
2,55 |
2,59 |
3,42 |
|
|
ke |
37/60 |
1,20 |
1,22 |
1,00 |
1,70 |
2,95 |
|
37/94 |
2,65 |
1,75 |
1,20 |
2,17 |
2,96 |
|
|
60/94 |
4,16 |
2,30 |
1,40 |
2,66 |
2,97 |
|
|
α |
37/60 |
2,40 |
1,65 |
2,08 |
2,23 |
3,04 |
|
37/94 |
2,91 |
2,04 |
1,95 |
2,34 |
3,03 |
|
|
60/94 |
3,45 |
2,45 |
1,82 |
2,45 |
3,03 |
|
|
ka |
37/60 |
2,52 |
1,36 |
2,03 |
2,23 |
2,66 |
|
37/94 |
2,80 |
1,87 |
1,80 |
2,23 |
2,74 |
|
|
60/94 |
3,10 |
2,42 |
1,57 |
2,23 |
2,82 |
|
Из данной таблицы следует, например, что наиболее точная аппроксимация частотных зависимостей модельных величин с помощью соотношения (4) возможна для структур 3, 4 и 5, а с наибольшей погрешностью аппроксимируются частотные зависимости коэффициентов обратного рассеяния и экстинкции структуры 1.
а) б)
в) г)
Рис. 3. Графики
экспериментальных (символы) и аппроксимационных (линии) частотных зависимостей
коэффициентов обратного рассеяния (а), экстинкции (б), коэффициента поглощения
(в)
и ослабления некогерентного излучения (г) исследованных структур снега.
Взаимосвязь экспериментальных значений и номеров структур:
.
С точки зрения влияния кластеров наибольший интерес представляют формы частотных зависимостей коэффициентов обратного рассеяния и экстинкции исследованных структур. В соответствии с теорией сильных флуктуаций коэффициент рассеяния сплошной случайной среды пропорционален f4. В миллиметровом диапазоне волн ни одна из исследованных структур не проявила подобные свойства.
Исключение составляет структура 1 в частотном интервале 60…90ГГц (см. таблицу 3), но при этом в более низкочастотном интервале 37,5…60ГГц показатель степени вдвое меньше. Этот, на первый взгляд, парадоксальный результат снова можно интерпретировать тем, что более длинноволновое излучение рассеивается в свежевыпавшем снеге не только на кристаллах льда, но также на их кластерах. Подтверждением этого служит также то, что, как видно из таблицы 3, в низкочастотном интервале 37,5…60ГГц значения показателя степени η частотной зависимости коэффициента экстинкции ke для всех структур, за исключением структуры 5, не превосходят 1,7. Кроме того, в случае структуры 3 такие низкие значения показателя степени относятся ко всему частотному интервалу 37,5…94ГГц.
Таблица 4.
|
модельные величины |
номер структуры |
|||||
|
1 |
2 |
3 |
4 |
5 |
||
|
b |
η pq |
3,10
1,7 10-8 |
2,35 2,6 10-6 |
2,50 1,7 10-7 |
3,10 2,4 10-8 |
3,70 6 10-9 |
|
ke |
η pq |
2,3 3,2 10-6 |
2,00 7,8 10-5 |
1,20 3,7 10-4 |
2,30 3,2 10-6 |
3,00 4,5 10-7 |
|
α |
η pq |
2,40 10-6 |
2,05 1,9 10-5 |
1,80 9 10-6 |
2,40 10-6 |
3,00 2,3 10-7 |
|
ka |
η pq |
2,50 4,3 10-7 |
2,70 5 10-7 |
2,00 2,4 10-6 |
2,50 4,3 10-7 |
2,10 7,1 10-6 |
Структура 5 отличается от всех других тем, что представляет собой старый снег, просеянный на сетке с ячейками 1мм. Его объемная плотность заметно выше, чем у других структур. Как следует из [16], радиус корреляции l случайной двухкомпонентной дискретной среды связан с объемной плотностью и диаметром d шаровых частиц соотношением:
(6)
Применительно к структуре 5 это
означает, что эффективный размер неоднородностей не превышает 0,5мм, а,
следовательно, значительно меньше длин волн, использованных в данном
исследовании. Кроме того, из-за высокой объемной плотности (
), близкой к предельной, основными
элементами каркаса структуры 5 являются преимущественно одинарные ледяные
частицы, а не их кластеры. В соответствии с данными таблицы 3 для структуры 5
значения показателя степени для коэффициентов обратного рассеяния b
и
экстинкции ke
слабо
зависят от частоты излучения, особенно, для коэффициента экстинкции: η=2,95…2,97.
В случае коэффициента обратного рассеяния b
они
изменяются в интервале 3,4…4,0, причем максимальное значение (η=4,0)
наблюдается именно в длинноволновой части спектра. Таким образом, структура 5 -
единственная из всех, спектральные свойства рассеяния в которой, с одной
стороны, существенно определяются размерами частиц, а не их кластеров, с другой
стороны, наиболее близко согласуются с теорией сильных флуктуаций.
Коэффициент поглощения ka,
как известно [17], определяется тепловыми потерями излучения в среде. В
отсутствие рассеяния тепловые потери в сухом снеге определяются, очевидно, его
объемной плотностью и комплексной диэлектрической проницаемостью льда. В
диапазоне ММ волн мнимая часть комплексной диэлектрической проницаемости
пресноводного льда почти линейно зависит от частоты [13]. Вследствие этого в
нерассеивающем сухом снеге следует ожидать частотную зависимость коэффициента поглощения
в виде 
. При наличии рассеяния коэффициент
поглощения увеличивается, что, в свою очередь, может усиливать частотную
зависимость. Из данных, приведенных на рис.3в, следует, что показатель
степени для исследованных структур варьируется в пределах η=2,0…2,7,
при этом максимальное значение относится к структуре 5, в которой рассеяние
наиболее сильное.
Частотная
зависимость коэффициента ослабления некогерентного рассеяния α
определяется
частотными зависимостями коэффициента поглощения ka
и коэффициента обратного рассеяния b,
поскольку 
. Из рис.3г следует, что показатель
степени частотной зависимости α
варьируется в пределах 1,8…3,0.
4. Выводы
Выполнено экспериментальное исследование спектральных свойств ослабления, рассеяния и поглощения миллиметровых волн в сухом свежевыпавшем снеге. Обнаружено сильное влияние кластеров на рассеяние миллиметровых волн в сухом свежевыпавшем снеге, вследствие которого частотные зависимости ослабления и рассеяния значительно слабее теоретических, рассчитанных в приближении теории сильных флуктуаций.
Авторы выражают глубокую благодарность Гордееву К.В, Рыкову К.Н. и Сунгурову Е.С. за помощь при проведении экспериментальных работ.
Литература
1. Долов М. А., Халкевич В.А. Физика снега и динамика снежных лавин. –Труды ВГИ. 1972. Вып. 23. С. 3-327.
2. Барабаненков Ю.Н. Многократное рассеяние волн на ансамбле частиц и теория переноса излучения // Успехи физ. наук. 1975. Т.117. Вып.1. С. 49-78.
3. Рыжов Ю.А., Тамойкин В.В., Татарский В.И. О пространственной дисперсии неоднородных сред // Изв. ВУЗов – Радиофизика. 1965. Т.48. Вып. 2. С. 656-665.
4. Tsang L., Kong J. A. Scattering of electromagnetic waves from random media with strong permittivity fluctuations // Radio Sci. 1981. Vol.16. No. 3. pp. 303-320.
5. Голунов В.А. Когерентное ослабление электромагнитных волн в слабо поглощающих плотных случайных дискретных (снегоподобных) средах // Радиотехника и электроника. 2015. Т.60. №1. С.31-37.
6. Голунов В.А. Тепловое излучение сухого однородного снежного покрова в диапазоне ММВ. // Зарубежная радиоэлектроника. Успехи современной радиоэлектроники. 2002. № 6. С. 35-44.
7. Golunov V. A., Barabanenkov Yu.N. Radiometric methods of measurement of the total reflectivity, the total transmissivity and the coherent transmissivity of a weakly absorbing random discrete medium layer in the millimeter wavelengths range // Proc. Progress In Electromagnetics Research Symp. Moscow, Russia, August 19-23, 2012. Р.1415-1418.
8. Kubelka P. New contributions to the optics of intensely light-scattering materials. Part I. // J. Opt. Soc. Am. 1948. Vol. 38, No.5, pp. 448-457.
9. Голунов В.А., Коротков В.А., Соколов А.В. Отражение и пропускание миллиметровых волн слоем случайной дискретной среды // Электромагнитные волны и электронные системы. 1997. Т. 2. № 1. С. 39 - 46.
10. Wiesman A., Mätzler C. Microwave emission model of layered snowpacks // Remote Sensing of Environment. 1999, Vol. 70, pp. 307-316.
11. Pulliainen J.T., Grandell J., Hallikainen M.T. HUT snow emission model and its applicability to snow water equivalent retrieval. // IEEE Trans. on Geosci. Remote Sensing. 1999, Vol. GE-37, No. 3, pp.1378-1390.
12. Голунов В.А. Результаты исследования применимости двухпотоковой теории Кубелки-Мунка к описанию переноса излучения в рассеивающем (снегоподобном) слое при коллимированном освещении (приеме) // Тез. XII Всерос. открытой конф. "Современные проблемы дистанционного зондирования Земли из космоса". М., ИКИ РАН, 2014. С.242.
13. Голунов В.А., Коротков В.А., Сухонин Е.В. Эффекты рассеяния при излучении миллиметровых волн атмосферой и снежным покровом. Итоги науки и техники, сер. Радиотехника. т.41. М.: ВИНИТИ. 1990. С.68-136.
14. Ван де Хюлст. Рассеяние света малыми частицами. М.: Иностранная литература. 1961.
15. Teschl F., Randeu W. L., Teschl R. Microwave scattering from ice crystals: how much parameters can differ from equal volume spheres // Adv. Geosci., 2010, Vol. 25, pp.127–133.
16. Stogryn A. Correlation functions for random granular media in strong fluctuation theory // IEEE Trans. 1984, Vol. GE-22, No 2, pp.150-154.
17. Рытов С.М., Кравцов Ю.А., Татарский В.И. Введение в статистическую радиофизику. Ч.2 – Случайные поля. М.: Наука. 1978.