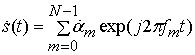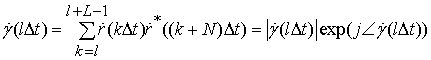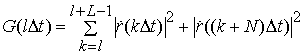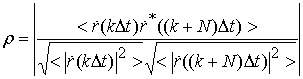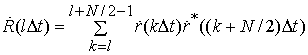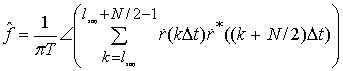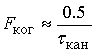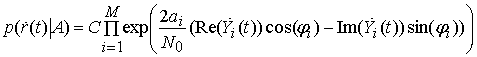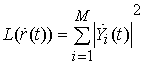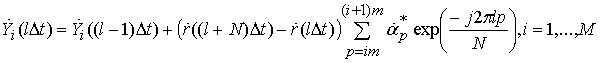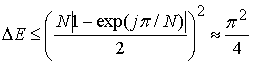УДК 621.391.01

АЛГОРИТМЫ ОБНАРУЖЕНИЯ OFDM СИГНАЛОВ В СИСТЕМАХ СИНХРОНИЗАЦИИ

Л. Е. Назаров ¹, А. С. Зудилин ²

¹Фрязинский филиал Института радиотехники и электроники им. В.А.Котельникова РАН, г. Фрязино

²АО «Информационные спутниковые системы» им. академика  М.Ф.Решетнева, г. Железногорск

 

Статья поступила в редакцию 9 сентября 2016 г.

Аннотация. Приведены результаты по разработке и исследованию алгоритмов некогерентного обнаружения OFDM сигналов-преамбул, используемых для синхронизации в системах передачи дискретных сообщений по каналам с многолучевым распространением сигналов.

Разработанные алгоритмы обнаружения основаны на использовании устойчивого алгоритма текущего спектрального анализа, являются более эффективными по производительности по отношению к алгоритму обнаружения на основе быстрого спектрального преобразования в базисе Фурье. Производительность рассматриваемых алгоритмов обнаружения определяется характеристиками каналов передачи, в частности, отношением частотной полосы сигналов к полосе когерентности канала передачи.

Алгоритмы обнаружения синхронизирующих OFDM сигналов обеспечивают повышение вероятности правильного обнаружения для многолучевого канала распространения сигналов по отношению к выделению одного луча за счет суммирования энергии составляющих лучей - для модели двухлучевого канала энергетический выигрыш достигает 2 дБ.

Ключевые слова: OFDM сигналы, синхронизация, вероятность обнаружения, быстрое преобразование Фурье, текущий спектральный анализ.

Abstract. Orthogonal frequency division multiplexing (OFDM) is popular technique in broadband wireless communications due to its advantage to combat channel multi-path and to provide high spectral efficiency. The drawback of OFDM systems is its high sensitivity to synchronization non idealities between the transmitter and receiver oscillators. Specifically incorrect timing synchronization can cause interference between successive symbols and can lead to a severe performance degradation. In addition, a carrier-frequency offset induces an amplitude reduction of the useful signal and provokes interference between adjacent subcarriers. In this paper the problem synchronization in OFDM systems (the detection, symbol timing and carrier-frequency evaluation) is examined and new algorithms of OFDM signal-preamble detection are proposed. The base of these algorithms is recursive sliding discrete Fourier transform that is more efficient that usage of Fast Fourier Transform.

Key words: OFDM signals, synchronization, error performance of detection,  FFT, recursive sliding discrete transform.

 

Введение

Сигналы с ортогональным частотным мультиплексированием известны в литературе как OFDM сигналы (orthogonal frequency division multiplexing) [1-3]. С их использованием возможна организация надежной связи по каналам с многолучевым распространением сигналов, обусловливающее наличие мультипликативных помех (частотно-селективные замирания сигналов), явление межсимвольной интерференции и нестационарность каналов передачи, а также по каналам с аддитивными канальными помехами естественного и индустриального происхождения [2-4].

Полезным свойством OFDM сигналов является возможность адаптивного формирования формы спектра, включая формирование спектров оконного типа с вариацией их ширины и расположения в рабочем частотном диапазоне.

Эти свойства определяют интенсивное использование OFDM сигналов в качестве базовых сигналов в ряде современных наземных и спутниковых цифровых системах связи, в системах программируемого радио [3].

OFDM сигналы представляют сумму парциальных гармонических сигналов, ортогональных в усиленном смысле на интервале времени определения [3]. При формировании и приеме этих сигналов используется алгоритм быстрого спектрального преобразования в базисе Фурье (БПФ) [5].

Недостатком OFDM сигналов является большие значения пик-фактор [1], что приводит к возникновению аддитивных интермодуляционных помех на выходе передатчика как нелинейного устройства. Проблемы оценивания мощности интермодуляционных помех и исследования их спектральных характеристик рассмотрены в работах [6-13].

Другая проблема обусловлена большими значениями внеполосных излучений OFDM сигналов. Для ее решения в работах [14,15] рассмотрен класс OFDM сигналов на основе манипуляции с непрерывной фазой с минимальным сдвигом частоты.

При использовании OFDM сигналов требуется выполнение синхронизации (временной, частотной) с достаточно высокой точностью [3,16]. Традиционно процедура синхронизации включает два этапа: обнаружение синхронизирующих сигналов и оценка параметров линии передачи; уточнение и сопровождение оценочных значений параметров линии передачи в случае ее нестационарного поведения.

В настоящей работе приведены результаты по разработке производительных алгоритмов начальной синхронизации (первый этап) для синхронизирующих OFDM сигналов (преамбул). Разработанные алгоритмы основаны на использовании устойчивого алгоритма текущего спектрального анализа [5].

 

1. Постановка задачи

OFDM сигналы  в области видеочастоты представляют сумму  парциальных гармонических сигналов, ортогональных на интервале определения длительностью  [3]

.                                                         (1)

Символы  в блоке  задаются сигнальным «созвездием» на основе входной последовательности длительностью ;  - объем алфавита . Для сигналов с двоичной фазовой манипуляцией (ФМ2) имеем . Ортогональность парциальных сигналов в усиленном смысле обеспечивается выбором частот .

Для решения задачи обнаружения синхронизирующие OFDM сигналы должны обладать «классическими» свойствами - минимизация боковых лепестков, кнопочность функции неопределенности, равномерность спектральной плотности в рабочей частотной полосе. Эти качества обеспечиваются выбором соответствующих символов () при формировании OFDM сигналов (1).

Известные методы синхронизации OFDM сигналов условно можно разделить на два общих класса - на основе защитных интервалов (префиксов), зависящих от передаваемой информации, и на основе использования преамбул, известных для приемных устройств [16].

При использовании алгоритмов синхронизации из первого класса обнаружение и оценка параметров канала задаются максимумом двумерной функции правдоподобия  с аргументами времени  и частоты  [17]

.                                 (2)

,          (3)

,                                   (4)

.                                    (5)

Здесь  - фаза комплексной величины ,  - время дискретизации.

Оценки времени задержки  и центральной частоты  имеют вид

,                    (6)

.                                                                (7)

При использовании алгоритмов синхронизации из второго класса обнаружение и оценка параметров канала осуществляется путем последовательного вычисления и анализа корреляций  для синхронизирующих OFDM сигналов-преамбул, обладающих свойством симметричности  [18] (свойством сопряженной симметричности  для OFDM сигналов-преамбул, используемых в стандарте IEEE 802.16e (WiMAX)),

.                                  (8)

Оценка времени задержки  и частоты  в этом случае имеют вид

,                                      (9)

.                           (10)

Приведенные алгоритмы обнаружения на основе соотношений (2), (8) являются подоптимальными по отношению к обработке входной реализации  для модели однолучевого канала, их эффективность снижается для многолучевых каналов [18]. Актуальной является задача разработки более эффективного алгоритма обнаружения синхронизирующих OFDM сигналов-преамбул для однолучевого и многолучевого каналов. Данный алгоритм также должен обладать высокой производительностью обработки.

Суть задачи - разработка производительного алгоритма обнаружения синхронизирующих OFDM сигналов-преамбул с большей помехоустойчивостью по отношению к рассмотренным алгоритмам (2), (8). Основу данного алгоритма составляет устойчивый алгоритм текущего спектрального анализа.

 

2. Модель многолучевого канала передачи

Сигналы на выходе канала с импульсной характеристикой  и с аддитивным шумом  задаются соотношением [19]

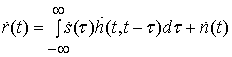.                                                    (11)

Для однолучевого стационарного канала имеем

.                                           (12)

Здесь  - нормирующий коэффициент,  - временная задержка сигналов;  - смещение частоты относительно центральной частоты  за счет эффекта Доплера либо за счет нестабильностей генераторов передатчика и приемника.

Основными статистическими характеристиками каналов с многолучевым распространением сигналов являются: частотная полоса когерентности , длительность импульсного отклика канала , время стационарности канала , доплеровское уширение  [19]. Данные характеристики определяют выбор соответствующих сигнальных конструкций и методов их обработки при помехоустойчивом приеме и синхронизации.

Характеристики  и  связаны приближенным соотношением [19]

.                                                                               (13)

Для систем подвижной связи при использовании модели с плотным размещением рассеивающих элементов частотная полоса когерентности определяется соотношением [19]

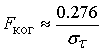.                                                                             (14)

Здесь  - среднеквадратичное отклонение параметра .

При расширении полосы сигналов  при условии  возникают частотно-селективные замирания сигналов, которые наряду с аддитивными помехами являются одними из основных факторов снижения надежности передачи информации.

Исследованию статистических характеристик многолучевых каналов (каналы наземных систем подвижной связи сотового формата, каналы спутниковых систем подвижной связи и телекоммуникаций, каналы ионосферной и тропосферной связи) посвящено большое количество работ. Для каналов спутниковых подвижных систем связи значения  получены экспериментально, например, для сельской местности  нсек [20], в соответствии с (13) полоса когерентности  МГц.

Приведем также характеристики канала системы связи сотового формата 4G с использованием OFDM сигналов:  мкс,  МГц, ,  мкс [16], в соответствии с (14) полоса когерентности  кГц.

 

3. Алгоритмы обнаружения синхронизирующих OFDM сигналов

Алгоритмы оптимального обнаружения, реализующие статистические правила принятия решений (правило Неймана-Пирсона, правило максимального правдоподобия [20]), основаны на анализе функции правдоподобия . Здесь  - простая гипотеза относительно наличия или отсутствия синхронизирующего сигнала.

При использовании синхронизирующих OFDM сигналов с частотной полосой  для канала с полосой когерентности  при условии  и при наличии канальной помехи в виде аддитивного белого гауссовского шума (АБГШ) функция правдоподобия определяется соотношением [19]

. (15)

Здесь  - нормирующий множитель;  - амплитуды парциальных сигналов на входе решающего устройства; 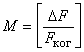,  - целая часть ;

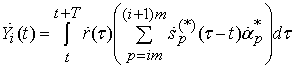, ,  - комплексное сопряжение.

 

Для однолучевого канала имеем , .

Выражение (15) соответствует разбиению множества парциальных сигналов на подмножества объемом  для полос когерентности , начальные фазы ,  при вычислении корреляций  являются статистически независимыми случайными величинами с равномерной плотностью распределения .

После усреднения (15) по  имеем результирующее выражение [19]

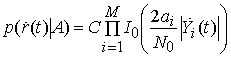.                                                        (16)

Здесь  - модифицированная функция Бесселя 1-го рода 0-го порядка.

Вычисление и анализ функции правдоподобия (16) определяет процедуру некогерентной обработки реализации  при обнаружении.

Вследствие монотонности функции  вычисление функции правдоподобия (16) можно заменить вычислением метрической характеристики , что обусловливает подоптимальную процедуру обнаружения синхронизирующих OFDM сигналов

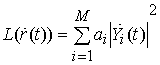.                                                                      (17)

Дальнейшее упрощение процедуры обнаружения заключается в предположении равенства амплитуд  парциальных сигналов при приеме, результирующее правило обнаружения основывается на вычислении и анализе метрической характеристики

.                                                                        (18)

Для однолучевого канала метрика  (18) определяет оптимальное некогерентное обнаружение сигналов.

Вычисление множества ,  в составе (15)-(18) можно осуществить, используя алгоритм БПФ размерностью  над дискретной функцией  длительностью ,  - время дискретизации. В этом случае на каждом такте вычисляется множество  спектральных составляющих ,  на основе спектрального преобразования дискретной реализации , вычисляется спектр мощности  и вычисляется функция правдоподобия  (16) или соответствующие метрические характеристики  (17) или (18). Данный подход на каждом такте требует выполнения  комплексных умножений [5]. Это определяет сложность реализации данного направления.

Повышение производительности процедуры обнаружения возможно, используя БПФ для спектрального анализа реализации  длительностью  с дискретными смещениями  [5]. Увеличение значения  приводит к энергетическим потерям по отношению к исходной процедуре обнаружения с применением БПФ на каждом такте - для  энергетические потери равны 1 дБ.

Альтернативу методу обнаружения OFDM сигналов с использованием БПФ относительно производительности и сложности реализации средствами цифровой вычислительной техники составляет процедура обнаружения на основе рекурсивного алгоритма текущего спектрального анализа [5].

Алгоритмы текущего спектрального анализа эффективны при вычислении спектральной компоненты  на анализируемом временном интервале  для реализации . Устойчивый алгоритм вычисления спектральной компоненты  для времени  на интервале длительностью  использует компоненту  и имеет вид [5]

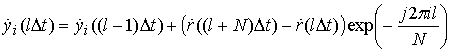.                (19)

Реализация (19) на каждом такте требует выполнения одного комплексного умножения.

Результирующая процедура вычисления метрической характеристики , определяемой соотношением (18), при использовании алгоритма текущего спектрального анализа (19) заключается в выполнении трех этапов.

На первом этапе для текущего такта вычисляются значения  с использованием значения , вычисленного на предыдущем такте

.            (20)

На втором этапе вычисляются последовательные значения  (18), которые сравниваются с порогом , его значение при использовании правила Неймана-Пирсона задается вероятностью ложной тревоги [19].

На третьем этапе при условии  принимается решение об обнаружении OFDM сигнала, оценка времени задержки .

Множители в (20)

, ,

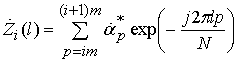имеют период  и вычисляются предварительно. Сложность реализации рассматриваемых процедур обнаружения определим числом комплексных умножений, требуемых при обработке дискретной реализации при поступлении отсчета  (на каждом такте). В этом случае снижение сложности реализации на каждом такте при использовании алгоритма обнаружения на основе текущего спектрального анализа (20) по отношению к алгоритму обнаружения на основе БПФ можно оценить соотношением

.                                                                                (21)

Для однолучевого канала имеем  и .

Соответствующее снижение сложности реализации приведенной процедуры обнаружения по отношению к процедуре обнаружения на основе БПФ с дискретными смещениями  оценивается соотношением 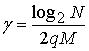. Величина  для рассмотренного выше канала системы связи 4G равна , в этом случае для  и  оценка .

Свойством рассматриваемого алгоритма (20) является возможность его реализации средствами параллельного программирования, так как вычисление значений  выполняется независимо для .

Приведенные процедуры обнаружения основаны на обработке входной реализации , дискретные отсчеты которой на выходе аналого-цифрового преобразования могут иметь временную неопределенность до . Это обусловливает наличие энергетических потерь  по отношению к точному временному положению синхронизирующего OFDM сигнала в анализируемой дискретной реализации. Оценка сверху значений  при условии точной частотной синхронизации имеет вид

 (4 дБ).                                    (22)

 

Обобщение приведенной процедуры некогерентного обнаружения для случая смещения частоты  сигналов относительно центральной частоты  заключается в вычислении множества значений  объемом ,  для каждой -ой спектральной составляющей,   - максимальное значение смещение частоты. Вычисление величин  осуществляется с использованием множителя в (20) в виде 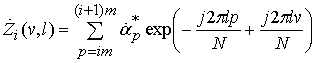. В этом случае при выполнении третьего этапа процедуры обнаружения при условии  принимается решение об обнаружении синхронизирующего OFDM сигнала и производятся оценки времени задержки  и смещения частоты .

 

4. Результаты моделирования

Исследование эффективностей приведенных алгоритмов обнаружения синхронизирующих OFDM сигналов произведено путем их компьютерного моделирования для канала АБГШ. Анализировались вероятности правильного обнаружения  при использовании правила Неймана-Пирсона для вероятности ложной тревоги  [1,19]. Число парциальных сигналов в синхронизирующем OFDM сигнале равно , сигнальное “созвездие” соответствовало ФМ2, символы  в блоке  (1) задавались символами М-последовательности [1].

 

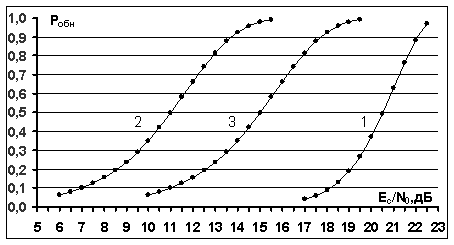
Рис.1. Вероятностные кривые обнаружения синхронизирующих OFDM сигналов-преамбул для однолучевого канала: 1 - алгоритм обнаружения сигналов со свойством симметричности на основе корреляций (8); 2 - алгоритм обнаружения сигналов на основе текущего спектрального анализа (точная временная синхронизация входных реализаций); 3 - алгоритм обнаружения сигналов на основе текущего спектрального анализа (отсчеты входных реализаций имеют временную неопределенность ).

 

На рис.1 приведены полученные вероятностные кривые, соответствующие применению приведенных алгоритмов обнаружения синхронизирующих OFDM сигналов для однолучевого канала. По оси абсцисс отложены значения сигнал/помеха ,  - энергия сигналов,  – спектральная плотность (односторонняя) АБГШ шума.

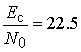Кривая 1 соответствует применению алгоритма обнаружения синхронизирующих OFDM сигналов со свойством симметричности на основе анализа корреляций  (8). Видно, что вероятность обнаружения  достигается при  дБ.

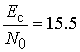Кривая 2 соответствует алгоритму обнаружения синхронизирующих OFDM сигналов на основе текущего спектрального анализа (20) при вычислении метрической характеристики (18) для случая точной временной синхронизации входных реализаций  и при отсутствии смещения центральной частоты  сигналов. Относительно параметров в соотношении (20) имеем , , . Видно, что вероятность обнаружения  достигается при  дБ, энергетический выигрыш по отношению к вероятностной кривой 1 достигает 7 дБ.

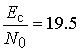Кривая 3 соответствует алгоритму обнаружения синхронизирующих OFDM сигналов на основе текущего спектрального анализа (20) при вычислении метрической характеристики (18) для наименее благоприятного случая - дискретные отсчеты  имеют временную неопределенность . В этом случае вероятность обнаружения  достигается при  дБ, энергетический проигрыш по отношению к вероятностной кривой 2 достигает 4 дБ, что согласуется с приведенным выше теоретическим анализом энергетических потерь, задаваемых соотношением (22).

На рис.2 приведены вероятностные кривые, соответствующие применению приведенного алгоритма обнаружения синхронизирующих OFDM сигналов на основе текущего спектрального анализа (20) для двухлучевого канала. Входная реализация  задавалась суммой сигнала первого (основного) луча и сигнала второго луча с временным смещением . Мощности первого и второго сигналов одинаковы, начальные фазы сигналов - статистически независимые случайные числа с равномерным законом распределения на сегменте . По оси абсцисс отложены значения сигнал/помеха ,  - энергия сигналов основного луча.

 

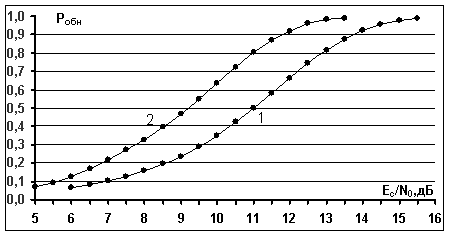
Рис.2. Вероятностные кривые обнаружения синхронизирующих OFDM сигналов-преамбул для двухлучевого канала: 1 - алгоритм обнаружения сигналов на основе текущего спектрального анализа (вычисление соотношения (20) с параметрами , , ); 2 - алгоритм обнаружения сигналов на основе текущего спектрального анализа (вычисление соотношения (20) с оптимальными параметрами , , ).

 

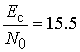Кривая 1 соответствует алгоритму обнаружения синхронизирующих OFDM сигналов на основе вычисления метрической характеристики (18) с использованием соотношения (20) с параметрами , , . Данная кривая совпадает с кривой 2 на рис.1, вероятность обнаружения  достигается при  дБ.

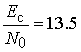Кривая 2 соответствует алгоритму обнаружения синхронизирующих OFDM сигналов на основе вычисления метрической характеристики (18) с использованием (20) с оптимальными параметрами , , , вычисленными для данной модели двухлучевого канала в соответствии с (13). Видно, что вероятность обнаружения  достигается при  дБ, энергетический выигрыш по отношению к кривой 1 достигает 2 дБ.

 

Заключение

Приведены результаты по разработке и исследованию алгоритмов некогерентного обнаружения OFDM сигналов-преамбул. Разработанные алгоритмы обнаружения перспективны для решения задачи начальной синхронизации систем передачи дискретных сообщений по каналам с многолучевым распространением сигналов.

Разработанные алгоритмы обнаружения основаны на использовании устойчивого алгоритма текущего спектрального анализа, являются более эффективными по производительности по отношению к алгоритму обнаружения на основе БПФ. Производительность рассматриваемых алгоритмов обнаружения определяется характеристиками каналов передачи, в частности, отношением частотной полосы сигналов к полосе когерентности канала передачи - для канала системы связи 4G снижение сложности реализации приведенных алгоритмов обнаружения по отношению к процедуре обнаружения на основе БПФ равно 2.5.

Алгоритмы обнаружения синхронизирующих OFDM сигналов обеспечивают повышение вероятности правильного обнаружения для многолучевого канала распространения сигналов по отношению к выделению одного луча за счет суммирования энергии составляющих лучей - для модели двухлучевого канала энергетический выигрыш достигает 2 дБ.

Точность оценки параметров OFDM сигналов-преамбул при синхронизации (время задержки, частота) с использованием рассматриваемых алгоритмов обнаружения на основе текущего спектрального анализа составляет направление перспективных исследований.

Работа выполнена при поддержке РФФИ (№16-07-00746).

 

Литература

1. Волков Л.Н., Немировский М.С., Шинаков Ю.С. Системы цифровой радиосвязи. Базовые методы и характеристики. М.: Эко-Трендз. 2005. 392 c.

2. Вишневский В.М., Ляхов А.И., Портной С.Л., Шахнович И.В. Широкополосные сети передачи. М.: Техносфера. 2005. 592 c/

3. Schulze H., Luders C. Theory and Applications of OFDM and CDMA. John Wiley & Sons, Ltd. The Atrium, England. 2005. 408 p.

4. Назаров Л.Е., Зудилин А.С. Алгоритмы компенсации сосредоточенных по спектру помех для сигналов с ортогональным частотным мультиплексированием. // Известия высших учебных заведений. Электроника. 2013. №6 (104). Стр. 45-51.

5. Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. М.: Мир, 1978. 848 с.

6. Шинаков Ю.С. Интермодуляционные помехи для сигналов OFDM в нелинейных устройствах с амплитудно-фазовой конверсией.// Проектирование и технология электронных средств. 2012. №3. Стр. 19-24.

7. Шинаков Ю.С. Пикфактор сигналов OFDM и нелинейные искажения в радиооборудовании систем беспроводного доступа. // Цифровая обработка сигналов. 2012. №4. Стр.58-65.

8. Шинаков Ю.С. Спектральная плотность мощности помехи нелинейных искажений в устройствах с амплитудно-фазовой конверсией. // Радиотехника и электроника. 2013. Т.58. №10. Стр. 1053-1064.

9. Шинаков Ю.С. Два способа вычисления мощности неискаженного сигнала на выходе нелинейного устройства с амплитудно-фазовой конверсией. // Радиотехника. 2016. №2. Стр. 66-71.

10. Клоков С.С., Шинаков Ю.С. Методы снижения пик-фактора сигнала в системах с технологией OFDM. // Сборник трудов “Технология информационного общества”. X Международная отраслевая научно-техническая конференция. Москва. 2016. С. 131-132.

11. Назаров Л.Е., Зудилин А.С. Оценивание мощности и эффективности интермодуляционных помех при ограничении огибающей OFDM-сигналов.// Радиотехника и электроника. 2015. Т.60. №5. Стр.522-528.

12. Назаров Л.Е., Зудилин А.С. Методики оценивания мощности интермодуляционных помех для сигналов с ортогональным частотным мультиплексированием.// Радиотехника и электроника. 2014. Т.59. №2. Стр.173-178.

13. Назаров Л.Е., Зудилин А.С. Оценка мощности интермодуляционных помех при предельном ограничении огибающей сигналов с ортогональным частотным мультиплексированием.// Журнал радиоэлектроники: электронный журнал. 2013. №6. URL: http://jre.cplire.ru/jre/jun13/1/text.pdf.

14. Назаров Л.Е., Зудилин А.С. Алгоритмы формирования и приема OFDM сигналов на основе манипуляции с минимальным сдвигом частоты. Журнал радиоэлектроники: электронный журнал. 2016. №8.

URL: http://jre.cplire.ru/jre/aug16/1/text.pdf.

15. Mahmoodi S., Saeedi H., Omidi M.J. OFDM-MSK: A Method for Sidelobe Suppression in OFDM Systems. // 20-th Iranian Conference on Electrical Engineering. Tehran. 2012. 15-17 May. P.1474-1477.

16. Бакулин М.Г., Крейнделин В.Б., Шлома А.М., Шумов А.П. Технология OFDM. М.: Горячая линия-Телеком. 2016. 360 с.

17. Van de Beek J.J., Sandell M., Borjesson P.O. ML Estimation of Time and Frequency Offset in OFDM Systems. // IEEE Transactions on Signal Processing. 1997. V.45. N7. P.1800-1805.

18. Steendam H., Moeneclaey M. Synchronization sensitivity of multicarrier systems. // European Transactions on Telecommunications. 2004. N15. P.223-234.

19. Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Изд. 2-е испр. Пер. с англ. М.: Издательский дом “Вильямс”. 2003. 1104 с.

20. Lutz E. Issues in satellite personal communication systems. // Wireless Network. 1998. N4. P.109-124.