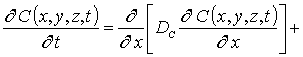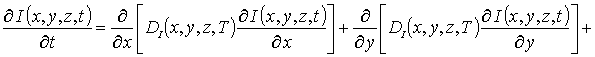О способе увеличения плотности полевых транзисторов в составе усилителя мощности

Е. Л. Панкратов, Е. А. Булаева

Нижегородский государственный университет им. Н.И. Лобачевского

 

Статья поступила в редакцию 9 августа 2016 г.

Аннотация. В данной работе рассматривается способ увеличения плотности полевых транзисторов в составе усилителя мощности, а так же уменьшения их размеров. Предлагаемый способ базируется на формировании гетероструктуры специальной конфигурации. После формирования гетероструктуры необходимые участки данной гетероструктуры легируются с помощью диффузии или ионной имплантации с целью формирования в них необходимых типов проводимости (p или n). Далее рассматривается оптимизированный отжиг примеси и/ или радиационных дефектов с целью формирования более компактных пространственных распределений концентраций примесей с одновременным увеличением равномерности распределения концентрации примесей в обогащенных ими областях. В данной работе также предлагается аналитическая методика прогнозирования технологического процесса. Данная методика позволяет одновременно учитывать пространственные и временные изменения параметров физических процессов (коэффициент диффузии примеси, предел растворимость примеси и другие), а также нелинейность рассматриваемых процессов.

Ключевые слова: усилитель мощности, полевые гетеротранзисторы, увеличение плотности гетеротранзисторов.

Abstract. In this paper we consider an approach to increase density of field-effect transistors framework a power amplifier. Framework the approach it is also possible to decrease dimensions of these transistors. The approach based on manufacturing heterostructure with special configuration. After the manufacturing required areas of the heterostructure have been doped by diffusion or by ion implantation to produce required type of conductivity (p or n). Further we consider optimized annealing of dopant and/or radiation defects to manufacture more compact spatial distributions of dopants with at the same time with increasing of homogeneity of dopant concentrations in doped areas. In this paper we also introduce an analytical approach for prognosis of technological process. The approach gives a possibility to take into account dependences of physical parameters (dopant diffusion coefficient, limit of solubility of dopant and other) on coordinate and at the same time on time. The approach gives also a possibility to take into account nonlinearity of the considered processed at the same time with the above dependences.

Keywords: power amplifier; field-effect heterotransistors; increasing of density of heterotransistors.

 

Введение

В настоящее время одним из актуальных вопросов твердотельной электроники является увеличение плотности элементов интегральных схем [1-6]. Данное увеличение плотности приводит к необходимости уменьшения размеров элементов интегральных схем. К настоящему времени разработаны несколько методов уменьшения размеров данных элементов. Одним из этих методов является выращивание тонкопленочных устройств [2-6]. Вторым методом является диффузионное или ионное легирование необходимых участков образцов или гетероструктур с дальнейшим лазерным или микроволновым отжигом примеси и/или радиационных дефектов [7-9]. Использование данных методов отжига приводит к формированию неоднородного температурного поля и, как следствия, к формированию неоднородности легируемой структуры и уменьшению размеров элементов интегральных схем. Еще одним способом изменения свойств легируемого материала является его радиационная обработка [10,11].

В данной работе рассматривается способ увеличения плотности полевых транзисторов в составе усилителя мощности. Для иллюстрации предлагаемого способа рассмотрим гетероструктуру, состоящую из подложки и эпитаксиального слоя. Эпитаксиальный слой включает в себя несколько секций, сформированных из других материалов. Данные секции легируются с помощью диффузии или ионной имплантации для обеспечения в них необходимого типа проводимости (p или n) с целью формирования полевых транзисторов так, как показано на рис. 1. После завершения легирования рассматривается отжиг примесей и/или радиационных дефектов. Основной целью данной работы является оптимизация длительности данного отжига.

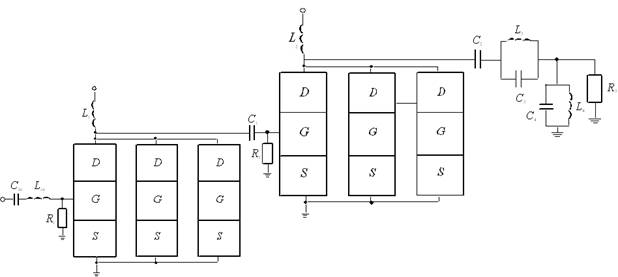
Рис. 1а. Схема усилителя мощности. Вид сверху

 

 

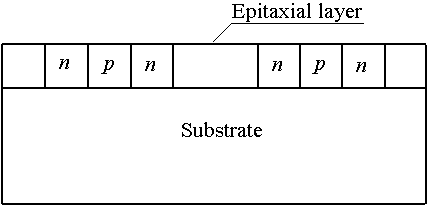
Рис. 1б. Гетероструктура, состоящая из подложки и эпитаксиального слоя с секциями, сформированными из других материалов, на базе которой сформирован усилитель мощности. Вид сбоку

 

Методика анализа

Пространственно-временное распределение концентрации примеси определим путем решения следующей краевой задачи

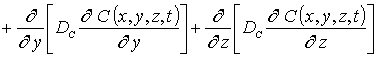                                  (1)

 

с граничными и начальным условиями

, , , ,

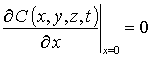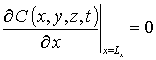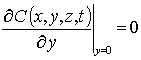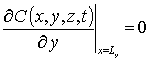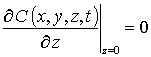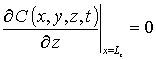, , C (x,y,z,0)=f   (x,y,z).               (2)

 

В соотношениях (1) и (2) введены следующие обозначения: C(x,y,z,t) - пространственно- временное распределение концентрации примеси, T - температура отжига, D_С - коэффициент диффузии примеси. Величина коэффициента диффузии определяется свойствами материалов в слоях гетероструктуры, скорости прогрева и охлаждения гетероструктуры (в соответствии с законом Аррениуса). Зависимости коэффициента диффузии от параметров могут быть аппроксимированы следующим соотношением [11-1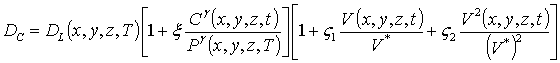3]

,  (3)

 

где D_L (x,y,z,T) - пространственная (за счет многослойности гетероструктуры) и температурная (по закону Аррениуса) зависимости коэффициента диффузии; P (x,y,z,T) - предел растворимости примеси; определяемый свойствами материала параметр g может принимать целые значения в интервале g Î[1,3] [12]; V (x,y,z,t) - пространственно-временное распределение концентрации радиационных вакансий; V^* - равновесное распределение вакансий. Концентрационная зависимость коэффициента диффузии подробно обсуждается в [12]. Следует заметить, что в случае диффузионного легирования радиационные повреждения отсутствуют и z₁= z₂= 0. Пространственно-временные распределения концентраций радиационных дефектов определялись путем решения следующей системы уравнений [11,13]

 

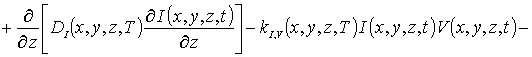
                                                                                                (4)

 

 

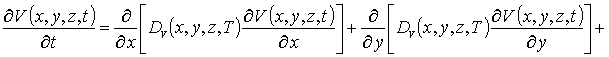
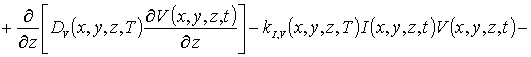
с граничными и начальными условиями

, , , ,

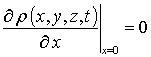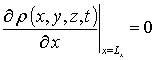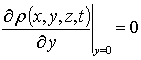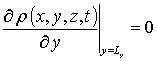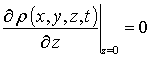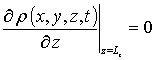, , r (x,y,z,0)=f_r  (x,y,z).                                           (5)

 

В системе уравнений (4) и условиях (5) используются следующие обозначения: r =I,V; I (x,y,z, t) - пространственно-временное распределение концентрации междоузельных атомов; D_r(x,y, z,T) - коэффициенты диффузии междоузельных атомов и вакансий; слагаемые V²(x,y,z,t) и I²(x,y,z,t) соответствуют образованию дивакансий и аналогичных комплексов междоузельных атомов; k_I,V(x,y,z,T), k_I,I(x,y,z,T) и k_V,V(x,y,z,T) - соответственно, параметры рекомбинации точечных дефектов и образования комплексов.

Пространственно-временные распределения концентраций дивакансий F_V (x, y,z,t) и аналогичных комплексов междоузельных атомов F_I (x,y,z,t) определим с помощью следующей системы уравнений [11,13]

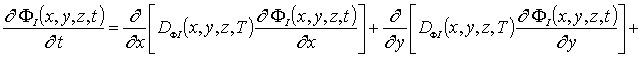
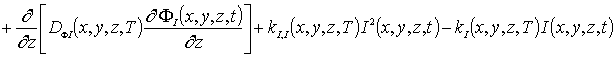                 (6)

 

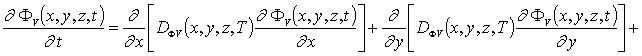
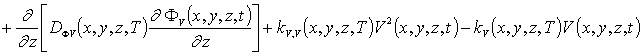
с граничными и начальными условиями

, , ,

, , ,
 

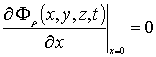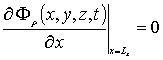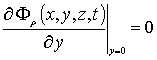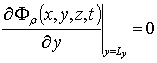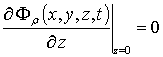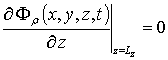F_r (x,y,z,0)=f_Fr (x,y,z).                                                                                                           (7)

 

В последних соотношениях введены следующие обозначения: D_Fr(x,y,z,T) - коэффициенты диффузии простейших комплексов точечных радиационных дефектов; k_I(x,y,z,T) и k_V (x,y,z,T) - параметры распада комплексов точечных дефектов.

Для определения пространственно-временного распределения концентрации примеси преобразуем уравнение (1) к следующей интегро-дифференциальной форме

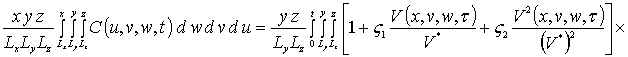
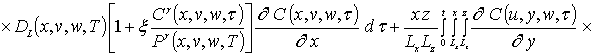
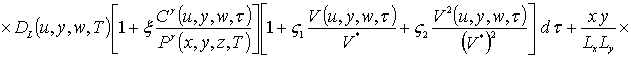
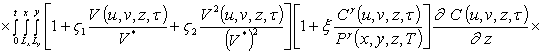
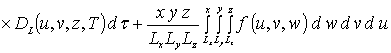.                                                             (1а)

 

Будем искать решение данного уравнения с помощью метода Бубнова- Галеркина [14]. В рамках данного метода определим решение уравнения (1а) в виде функционального ряда, близкого к решению линейного уравнения (1) (т.е. при x = 0) с усредненным коэффициентом диффузии, т.е.

,

где , c_n(c) = cos (p  n c/L_c). В данном случае рассматривается функциональный ряд, содержащий конечное число членов N. Подстановка данного ряда в уравнение (1а) позволяет получить

,

 

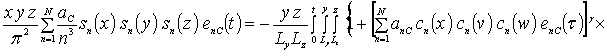
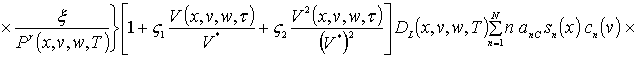
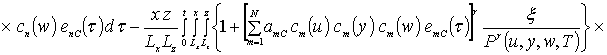
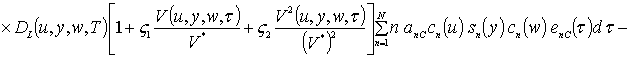
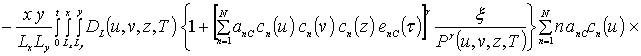
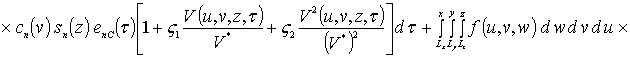
где s_n(c) = sin (p n c/L_c). Коэффициенты a_n определяется из условия ортогональности членов ряда на масштабе гетероструктуры. Данное условие позволяет получить соотношения для расчета коэффициентов a_n при любом количестве членов ряда N. В общем случае уравнения для искомых коэффициентов имеют вид

.

 

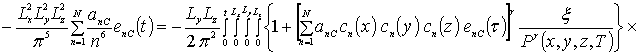
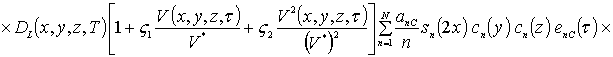
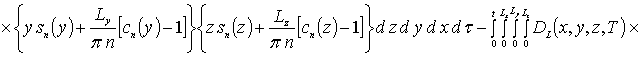
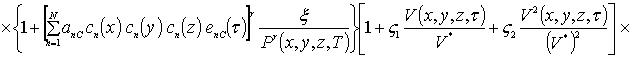
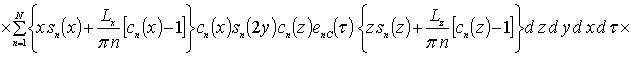
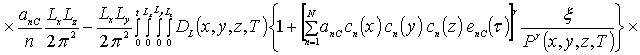
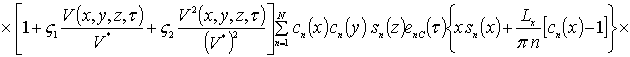
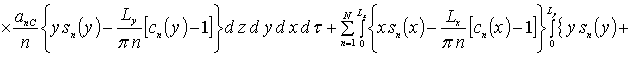
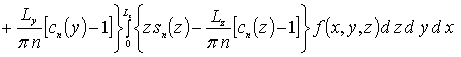В качестве примера при g = 0 получаем

.

 

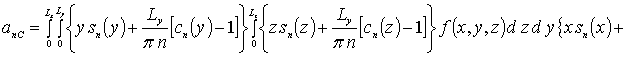
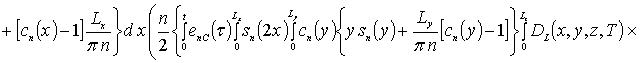
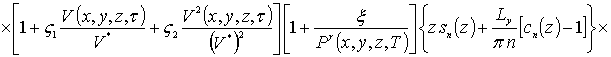
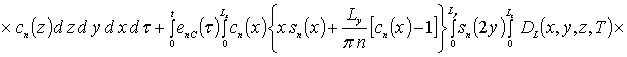
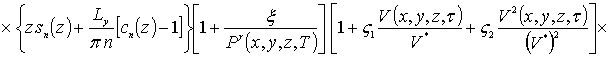
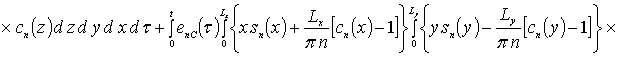
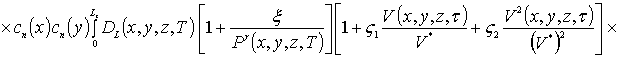
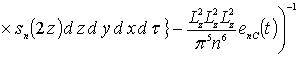При g = 1 получаем следующие соотношения для определения искомых параметров

,

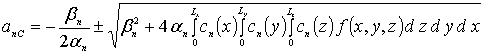где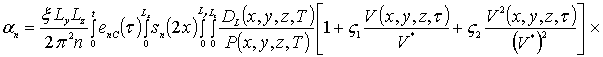

,

 

.

 

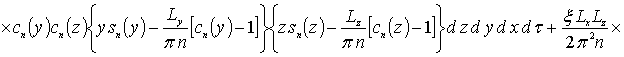
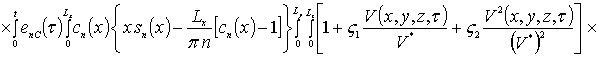
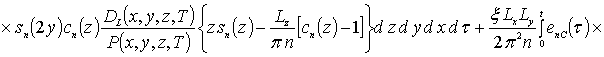
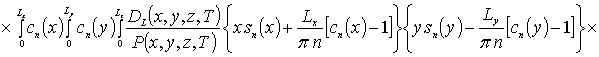
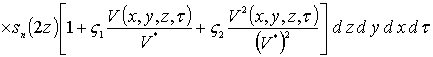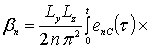
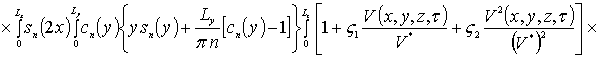
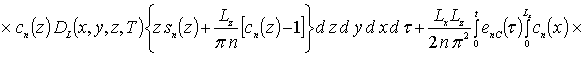
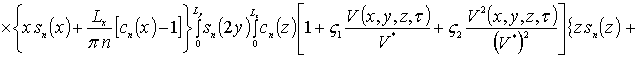
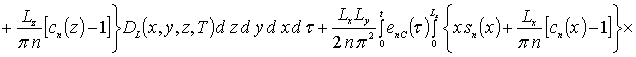
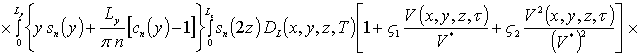
Аналогично могут быть получены соотношения для расчета коэффициентов a_n при больших значениях параметра g. Однако данные соотношения являются более громоздкими и приводиться не будут. Следует заметить, что рассматриваемый метод решения позволяет обходиться без сшивки решения на границе раздела между слоями гетероструктуры.

Уравнения системы (4) также решались методом Бубнова-Галеркина. Перед его применением преобразуем данные уравнения к следующей интегральной форме

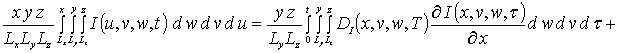
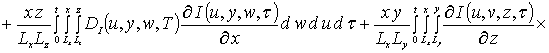                                (4а)

.

 

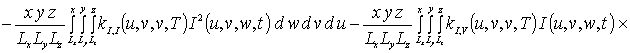
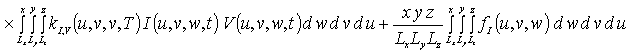
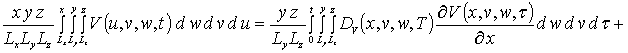
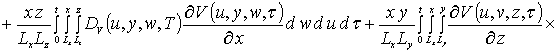
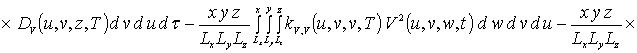
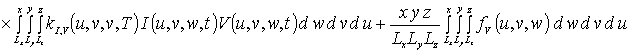Далее будем искать решение данной системы уравнений в виде следующих функциональных рядов

,

где a_nr - неизвестные пока коэффициенты. Подстановка данных рядов в систему уравнений (4а) приводит к следующему результату

.

 

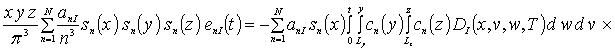
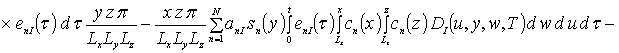
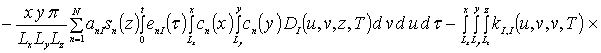
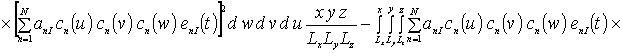
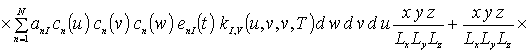
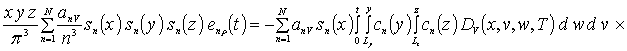
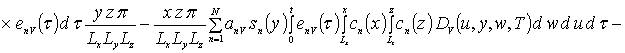
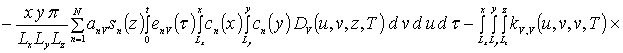
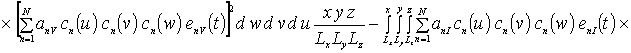
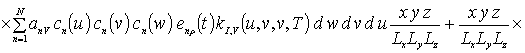
Коэффициенты a_nr определяется из условия ортогональности членов ряда на масштабе гетероструктуры. Данное условие позволяет получить соотношения для расчета коэффициентов a_nr при любом количестве членов ряда N. В общем случае уравнения для искомых коэффициентов имеют вид

.

 

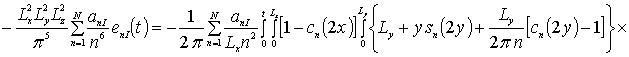
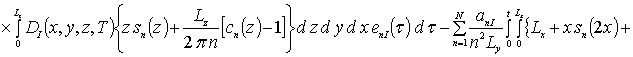
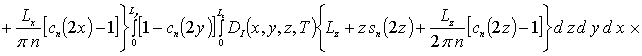
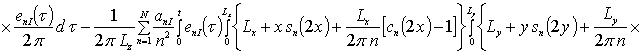
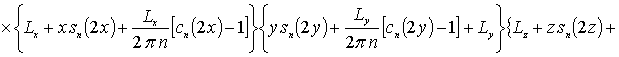
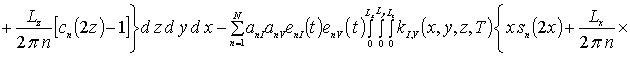
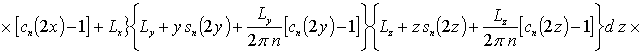
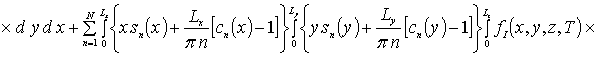
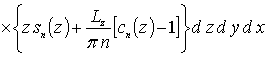
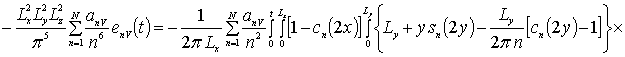
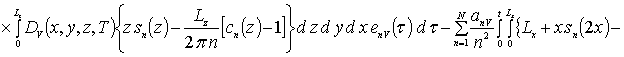
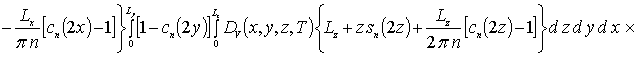
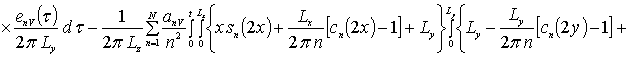
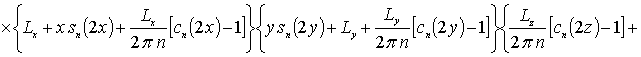
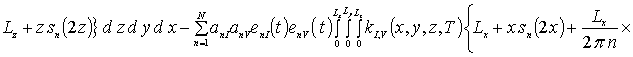
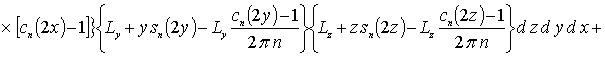
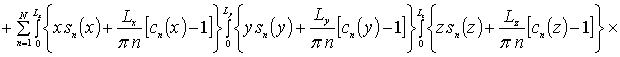
В окончательном виде соотношения для искомых параметров представимы в следующей форме

, ,

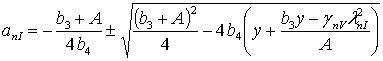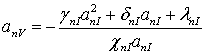где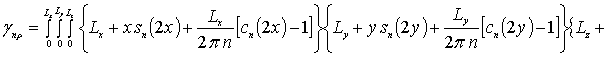

,

,

 

,

, ,

, ,

, , ,

, .

 

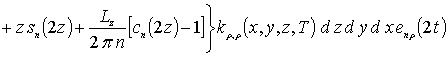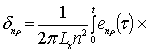
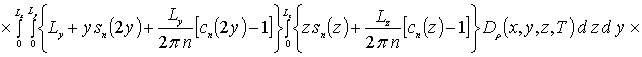
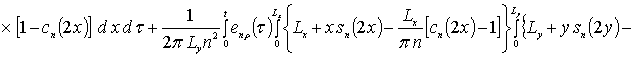
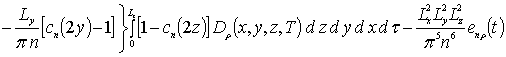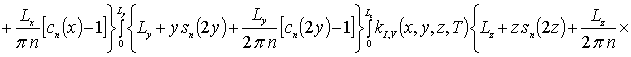
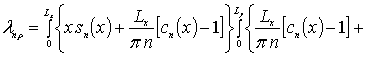
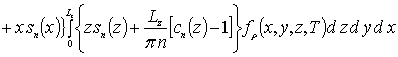Пространственно-временные распределения концентраций комплексов радиационных дефектов определим в виде следующего ряда

,

где a_nFr - неизвестные пока коэффициенты. Перед определением данных коэффициентов преобразуем систему дифференциальных уравнений (6) к интегральной форме

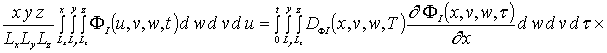
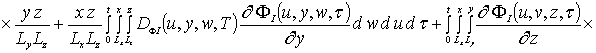
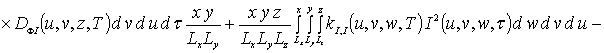
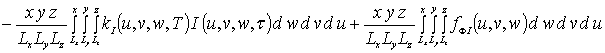                         (6а)

.

 

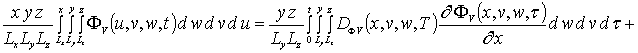
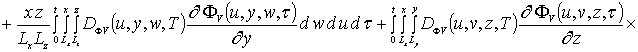
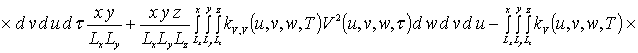
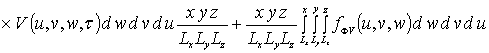Подстановка предлагаемой формы решения в виде функциональных рядов в систему уравнений (6а) приводит к следующему результату

.

 

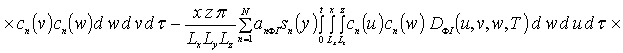
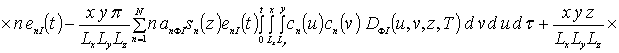
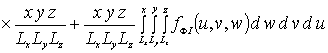
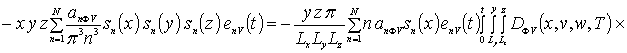
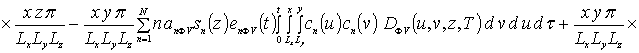
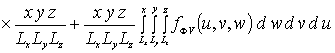Далее пользуясь ортогональностью базисных функций, входящих в предлагаемую форму решения рассматриваемых интегральных уравнений, определим коэффициенты a_nFr. Условие ортогональности приводит к следующей системе уравнений для определения искомых коэффициентов a_nFr

 

.

 

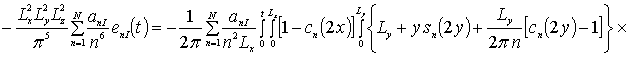
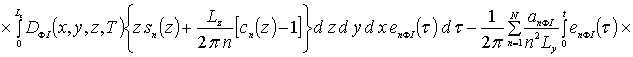
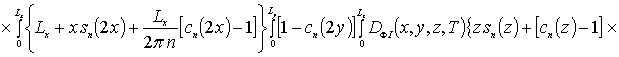
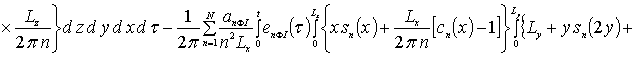
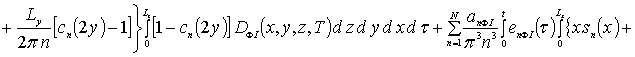
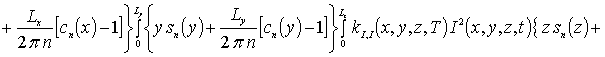
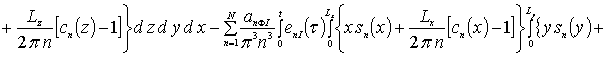
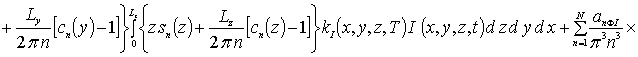
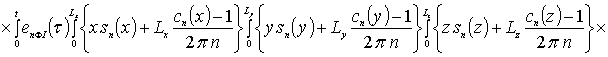
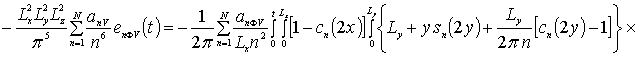
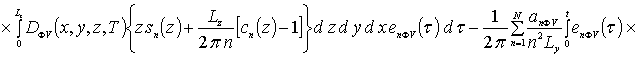
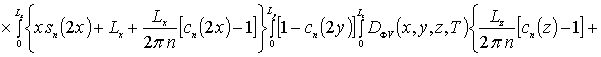
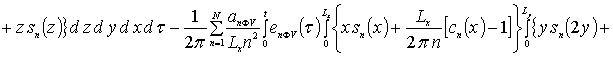
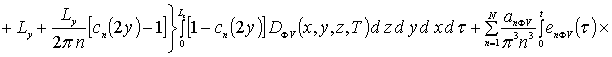
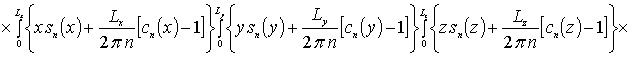
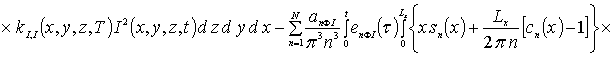
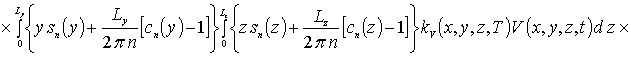
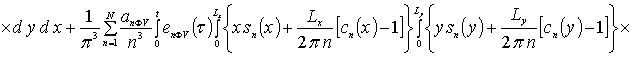
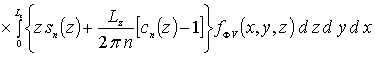Результаты анализа

В данном разделе проведем анализ пространственно-временного распределения концентрации примеси, введенной в эпитаксиальный слой с помощью диффузии (рис. 2а) или ионной имплантации (рис. 2б). Длительность отжига имеет одинаковые значения для всех кривых каждого рисунка. Увеличение номера кривой соответствует увеличению разницы между значениями коэффициента диффузии в слоях гетероструктуры. Из данных рисунков следует, что наличие границы раздела между слоями гетероструктуры позволяет увеличить абсолютное значение градиента концентрации примеси в направлении, перпендикулярном рассматриваемой границе раздела. Следствием данного результата является уменьшение размеров транзисторов, входящих в состав усилителя. Одновременно с увеличением рассматриваемого градиента увеличивается равномерность распределения концентрации примеси в обогащенной ею области.

 

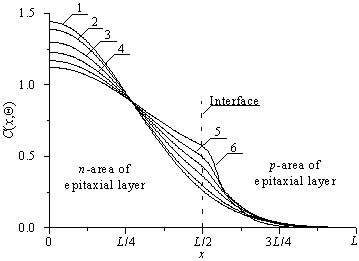
Рис.2а. Распределения концентрации введенной диффузионно примеси в представленной на рис. 1 гетероструктуре в направлении, перпендикулярном границе раздела между подложкой и эпитаксиальными слоями. Увеличение номера кривой соответствует увеличению разницы между значениями коэффициента диффузии примеси в слоях при условии, что коэффициент диффузии примеси в легированной области больше, чем в соседней

 

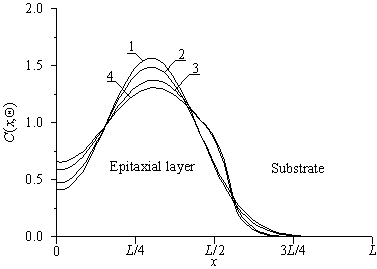
Рис. 2б. Пространственное распределение имплантированной примеси после отжига длительностью Q = 0,0048(L_x²+L_y²+L_z²)/D₀ (кривые 1 и 3) и Q = 0,0057 (L_x²+L_y²+L_z²)/D₀ (кривые 2 и 4). Кривые 1 и 2 – расчетные распределения в однородной структуре; кривые 3 и 4 - расчетные распределения примеси в двухслойной структуре при условии, что коэффициент диффузии примеси легированном слое больше, чем в соседнем

 

При выборе длительности отжига необходимо учитывать уменьшение по абсолютному значению градиента концентрации в окрестности границы раздела между эпитаксиальным слоем и подложкой с ростом длительности отжига. Уменьшение длительности отжига приводит к формированию более неоднородного распределения концентрации примеси (см. рис. 3а для диффузионного легирования и 3б для ионного легирования). Определим компромиссную длительность отжига в рамках введенного ранее критерия [15-20]. В рамках данного критерия аппроксимируем реальное распределение концентрации примеси с помощью идеального прямоугольного распределения y (x,y,z). Далее искомую длительность отжига определим из условия минимума среднеквадратической ошибки

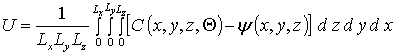.                   (8)

 

Зависимости оптимальной длительности отжига приведены на рис. 4. Следует заметить, что после проведения ионной имплантации необходимо проводить отжиг радиационных дефектов. В идеальном случае после проведения данного отжига примесь достигает границы раздела между слоями гетероструктуры. Если примесь не успевает достигнуть данной границы, целесообразно проводить дополнительный отжиг примеси. На рис. 4б приведены зависимости именно длительности дополнительного отжига. Необходимость отжига радиационных дефектов приводит к меньшим значениям оптимальной длительности отжига по сравнению с оптимальной длительностью отжига примеси, введенной диффузионно. Следует заметить, что использование диффузионного легирования не приводит к столь серьезным повреждениям, как в случае ионного легирования. Однако ионное легирование представляет интерес для легирования гетероструктур с существенно различающимися постоянными решетки, т.к. радиационное воздействие позволяет уменьшить механические напряжения в гетероструктуре [21].

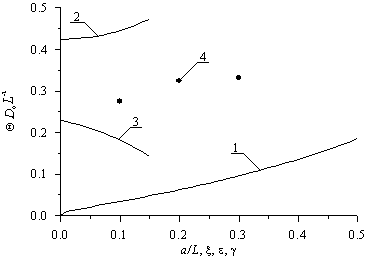
Рис.4а. Зависимости безразмерного оптимального времени отжига введенной диффузионно примеси, полученного из условия минимума среднеквадратической ошибки, от различных параметров гетероструктуры. Кривая 1 - зависимость времени отжига от отношения a/L и x = g = 0 при попарном равенстве коэффициентов диффузии. Кривая 2 - зависимость времени отжига от параметра e при a/L=1/2 и x = g = 0. Кривая 3 - зависимость времени отжига от параметра x при a/L=1/2 и e = g = 0. Кривая 4 - зависимость времени отжига от параметра g при a/L=1/2 и e = x = 0

 

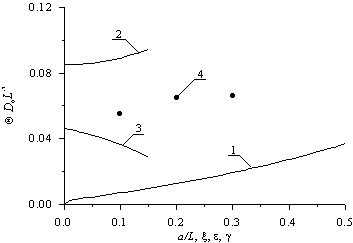
Рис.4б. Зависимости безразмерного оптимального времени отжига введенной с помощью ионной имплантации примеси, полученного из условия минимума среднеквадратической ошибки, от различных параметров гетероструктуры. Кривая 1 - зависимость времени отжига от отношения a/L и x = g = 0 при попарном равенстве коэффициентов диффузии. Кривая 2 - зависимость времени отжига от параметра e при a/L=1/2 и x = g = 0. Кривая 3 - зависимость времени отжига от параметра x при a/L=1/2 и e = g = 0. Кривая 4 - зависимость времени отжига от параметра g при a/L=1/2 и e = x = 0

 

Заключение

В данной работе проводился анализ изменения в пространстве и времени концентраций введенных с помощью диффузии и ионной имплантации примесей в процессе формирования усилителя мощности на базе полевых гетеротранзисторов. Сформулированы рекомендации по оптимизации отжига с целью уменьшения размеров гетеротранзисторов. Предложена аналитическая методика моделирования диффузионного и ионного типов легирования, позволяющая одновременно учесть и пространственные, и временные изменения параметров, а также нелинейность рассматриваемых процессов.

Литература

[1] S.A.Z. Murad, M.N. Md Isa, F.A. Bakar, R. Sapawi. Recent Advances in Electrical and Electronic Engineering. Vol. 9 (1). P. 63-67 (2016).

[2] Г. Волович. Современная электроника. № 2. С. 10-17 (2006).

[3] А. Керенцев, В. Ланин. Силовая электроника. №. 1. С. 34-38 (2008).

[4] А.О. Агеев, А.Е. Беляев, Н.С. Болтовец, В.Н. Иванов, Р.В. Конакова, Я.Я. Кудрик, П.М. Литвин, В.В. Миленин, А.В. Саченко. ФТП. Т. 43 (7). С. 897-903 (2009).

[5] Н.И. Волокобинская, И.Н. Комаров, Т.В. Матюхина, В.И. Решетников, А.А. Руш, И.В. Фалина, А.С. Ястребов. ФТП. Т. 35 (8). С. 1013-1017 (2001).

[6] A. Subramaniam, K. D. Cantley, E.M. Vogel. Active and Passive Electronic Components. Vol. 2013, ID 525017 (2013).

[7] K.K. Ong, K.L. Pey, P.S. Lee, A.T.S. Wee, X.C. Wang, Y.F. Chong. Appl. Phys. Lett. Vol. 89 (17), 172111-172114 (2006).

[8] H.T. Wang, L.S. Tan, E. F. Chor. J. Appl. Phys. Vol. 98 (9), 094901-094905 (2006).

[9] Ю.В. Быков, А.Г. Еремеев, Н.А. Жарова, И.В. Плотников, К.И. Рыбаков, М.Н. Дроздов, Ю.Н. Дроздов, В.Д. Скупов. Известия вузов. Радиофизика. Т.43 (3). С. 836-843 (2003).

[10] В.В. Козловский. Модификация полупроводников пучками протонов (С-Пб: Наука, 2003).

[11] В.Л. Винецкий, Г.А. Холодарь. Радиационная физика полупроводников (Киев: Наукова Думка, 1979).

[12] З.Ю. Готра. Технология микроэлектронных устройств (М: Радио и связь, 1991).

[13] P.M. Fahey, P.B. Griffin, J.D. Plummer. Rev. Mod. Phys. Vol. 61 (2). P. 289-388 (1989).

[14] М.Л. Краснов, А.И. Киселев, Г.И. Макаренко. Интегральные уравнения (М: "Наука", 1976).

[15] Е.Л. Панкратов. Микроэлектроника. Т. 36 (1). С. 33-39 (2007).

[16] E.L. Pankratov. Int. J. Nanoscience. Vol. 7 (4-5). P. 187–197 (2008).

[17] E.L. Pankratov. J. Comp. Theor. Nanoscience. Vol. 7 (1). P. 289-295 (2010).

[18] E.L. Pankratov, E.A. Bulaeva. J. Comp. Theor. Nanoscience. Vol. 10 (4). P. 888-893 (2013).

[19] E.L. Pankratov, E.A. Bulaeva. Int. J. Micro-Nano Scale Transp. Vol. 4 (1). P. 17-31 (2014).

[20] E.L. Pankratov, E.A. Bulaeva. Int. J. Nanoscience. Vol. 11 (5). P. 1250028-1250035 (2012).

[21] E.L. Pankratov, E.A. Bulaeva. J. Comp. Theor. Nanoscience. Vol. 11 (1). P. 91-101 (2014).