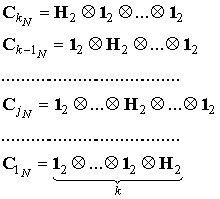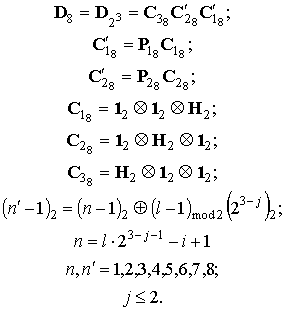УДК 621.391.81:621.396.96
Алгоритм сжатия когерентных дополнительных сигналов
Р. Н. Ипанов
Научно-производственное объединение «Специальная техника и связь»
Министерства внутренних дел Российской Федерации
Статья поступила в редакцию 12 сентября 2016 г.
Аннотация. Рассмотрен алгоритм сжатия радиолокационных сигналов, имеющих в окрестности центрального пика автокорреляционной функции область нулевых боковых лепестков. Данные сигналы, названные когерентными дополнительными сигналами, представляют собой пачку из двух когерентных фазокодоманипулированных импульсов, кодированных парой дополнительных последовательностей. Область нулевых боковых лепестков автокорреляционной функции когерентных дополнительных сигналов позволяет снизить порог обнаружения радиолокационных целей до уровня шумов, повышая тем самым вероятностные характеристики обнаружения. Также за счет относительно большой базы эти сигналы имеют высокие коэффициенты сжатия, что позволяет решать задачу разрешения близкорасположенных по дальности целей с близкими радиальными скоростями и измерять их координаты с высокими точностными характеристиками.
Устройство сжатия когерентных дополнительных сигналов состоит из входного регистра на N ячеек, процессора дискретного преобразования, имеющего N входов и два выхода, регистра сдвига на Q·N ячеек и сумматора, где N – число элементов в дополнительной последовательности, Q – скважность сигнала. Показано, что структурная схема устройства сжатия когерентных дополнительных сигналов представляет собой эквивалентную структурную схему согласованного фильтра, основным элементом которого является процессор дискретного преобразования. Алгоритм работы данного процессора представляет собой алгоритм быстрого преобразования Уолша-Адамара с упорядочением по Адамару, сигнальный граф которого с первой по предпоследнюю итерацию содержит дополнительные вещественные весовые коэффициенты «-1». Отчеты спектра дискретного преобразования для вычисления одной автокорреляционной функции снимаются с одной из N/2 пар его выходов. Таким образом, можно получить N/2 различных автокорреляционных функций по числу различных пар дополнительных последовательностей длины N.
Рассмотренный алгоритм сжатия когерентных дополнительных сигналов позволяет эффективно в реальном масштабе времени решать задачи разрешения и измерения координат групповых радиолокационных целей с близкими радиальными скоростями.
Ключевые слова: пачка импульсов, дополнительная последовательность, автокорреляционная функция, боковые лепестки, порог обнаружения, радиальная скорость, согласованный фильтр, преобразование Уолша-Адамара, сигнальный граф, весовой коэффициент.
Abstract. A compression algorithm for radar signals that has an area of zero sidelobes in the vicinity of the central peak of the autocorrelation function has been considered. These signals, which are called coherent additional signals, are a burst of two coherent phase-code-manipulated pulses coded by a pair of complementary sequences. The zero sidelobe area of the aucorrelation function of the coherent additional signals permits to reduce the threshold of detection of radar targets to the noise level, thus increasing the detection probability. Also, by virtue of the relatively large base these signals have high compression coefficients, which makes it possible to solve the problem of discerning targets that are closely located in space to each other and have close radial velocities as well as measuring their coordinates with high precision.
The device for compression of the coherent additional signals consists of the input register with N cells, a discrete transform processor with N inputs and two outputs, a shift register with Q·N cells and an adder, where N is the number of the elements in the complementary sequence and Q is the parameter inverse to the duty ratio. It has been shown that the block diagram of the coherent additional signal compression device is an equivalent block diagram of a matched filter, the discrete transform processor being the main element of it. The algorithm of the processor’s operation is an algorithm of fast Walsh–Hadamard transform (Haramard ordered), the signal graph of which contains complementary real weighing coefficients «‑1» from the first to the penultimate iteration. The reports of the discrete transform spectrum for computing one autocorrelation function are taken from one of the N/2 pairs of its outputs. Therefore, N/2 various autocorrelation functions can be obtained — according to the number of the different pairs of the complementary sequences N long.
The considered compression algorithm for the coherent additional signals makes it possible to achieve effective real-time solutions of the problems of discerning and measuring the coordinates of grouped targets of the radar that have close radial velocities.
Key words: burst of pulses, complementary sequences, autocorrelation function, sidelobe, signal detection threshold, radial velocity, matched filter, Walsh-Hadamard transform, signal graph, weighting coefficient.
Введение
Как известно, принятые на вооружение вероятным противником межконтинентальные баллистические ракеты (МБР) для повышения вероятности прорыва системы противоракетной обороны оснащаются комплексом средств преодоления (КСП). Совокупность движущихся по заданным траекториям боеголовок, элементов конструкции головной части МБР, КСП и последней ступени ракетоносителя образуют сложную баллистическую цель (СБЦ). Селекция элементов СБЦ на внеатмосферном участке траектории позволяет увеличить время предупреждения о ракетном нападении, а значит и время для принятия решения высшим руководством страны на ответные действия.
Задача разрешения элементов СБЦ, таким образом, сводится к задаче разрешения групповых (распределенных по дальности) целей, имеющих близкие радиальные скорости.
В РЛС сопровождения целей для решения задач разрешения элементов СБЦ и измерения их координат используются ФКМ сигналы, кодируемые усеченными М-последовательностями. Уровень боковых лепестков автокорреляционной функции (АКФ) ФКМ сигнала, кодируемого периодом М-последовательности, не позволяет понизить порог обнаружения целей ниже их уровня.
Когерентные дополнительные сигналы (КДС) представляют собой последовательность двух когерентных ФКМ импульсов, каждый из которых кодирован одной из дополнительных последовательностей [1].
АКФ КДС в окрестности центрального пика имеет область нулевых боковых лепестков, что позволяет снизить порог обнаружения групповых целей до уровня шумов, повышая тем самым вероятностные характеристики обнаружения. Также за счет относительно большой базы эти сигналы имеют высокие коэффициенты сжатия, что позволяет решать задачу разрешения близкорасположенных по дальности целей с близкими радиальными скоростями, то есть элементов СБЦ, и измерять их координаты с высокими точностными характеристиками.
Цель работы – разработка структурной схемы устройства сжатия КДС, алгоритм работы которого включает в свой состав быстрое преобразование Уолша (БПУ), что позволяет эффективно в реальном масштабе времени решать задачи разрешения и измерения координат групповых целей с близкими радиальными скоростями.
Структурная схема устройства сжатия когерентного дополнительного сигнала
Рассмотрим структурную схему устройства сжатия КДС (рис.1) и покажем, что устройство, построенное по такой схеме, представляет собой согласованный фильтр (СФ) КДС.
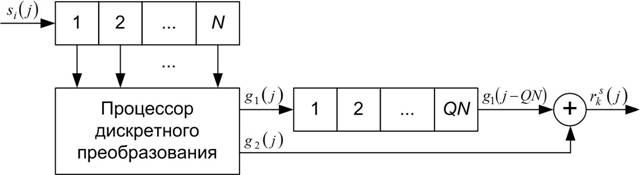
Рис.1. Эквивалентная структурная схема СФ КДС
Данное устройство состоит из входного регистра на N ячеек, процессора дискретного преобразования, имеющего N входов и два выхода, регистра сдвига на Q·N ячеек и сумматора.
Основным элементом данного устройства является процессор дискретного преобразования, алгоритм работы которого описывается следующим математическим выражением:
- вектор
входного сигнала дискретного преобразования;
-
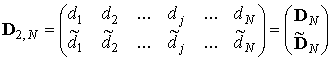матрица, состоящая из пары дополнительных последовательностей [1];
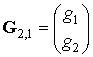- вектор выходного сигнала (спектра) дискретного преобразования.
Чтобы доказать, что на рис.1 представлена эквивалентная структурная схема СФ КДС, достаточно показать, что импульсная характеристика (ИХ) данного устройства представляет собой КДС (точнее ИХ должна быть зеркальной к самому сигналу). Для этого на вход устройства необходимо подать дельта-функцию Дирака, а на выходе получить КДС.
Т.о., если вместо КДС на вход данного устройства подать дельта-функцию, то огибающая входного сигнала в векторной форме будет иметь следующий вид [1]:
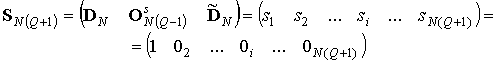(2)
На
рис.1 на вход устройства в данный момент времени (номер такта j) поступает элемент вектора (2) 
, т.е. в первый такт – «единица», а в остальные – «нули». На выходе
устройства получаем отсчеты АКФ КДС 
[1], которые в данном случае должны
совпадать с отсчетами самого КДС.
Таблица 1.
|
Номер такта |
|
|
|
|
|
1 |
|
|
0 |
|
|
2 |
|
|
0 |
|
|
… |
… |
… |
… |
… |
|
j |
|
|
0 |
|
|
… |
… |
… |
… |
… |
|
|
|
|
0 |
|
|
|
|
|
0 |
|
|
|
0 |
0 |
0 |
0 |
|
… |
… |
… |
… |
… |
|
|
0 |
0 |
0 |
0 |
|
|
0 |
0 |
|
|
|
|
0 |
0 |
|
|
|
… |
… |
… |
… |
… |
|
|
0 |
0 |
|
|
|
|
0 |
0 |
|
|
В таблице 1 представлены
отсчеты сигналов на выходе процессора дискретного преобразования 
и 
, на выходе регистра сдвига 
и на
выходе всего устройства 
с 1-го по 
-й такт его работы. Из данной таблицы
следует, что через тактов на выходе устройства (рис.1)
будут получены отсчеты КДС (его ИХ):
(3)
Т.о., ИХ устройства, структурная схема которого изображена на рис.1, представляет собой КДС, а значит, данная схема является эквивалентной структурной схемой СФ КДС.
Существует 
пар дополнительных последовательностей
длины N, где 
, 
, 
- множество натуральных чисел. Если
перейти от последовательностей к кодам, то получим семейство из N взаимно ортогональных двоичных кодовых
слов 
длины N, которое называется D-кодом порядка k [2].
Кодовые слова 
и 
называются
парными, если:
Представим кодовые слова D-кода в векторном виде:
,
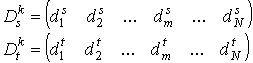(5)
где 
.
Тогда прямая 
и дополнительная 
последовательности, где 
, связаны с парными кодовыми словами D-кода в соответствии с выражениями:
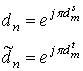(6)
Из (6) следует, что если
построить матрицу из пар дополнительных последовательностей
длины N, то данные пары последовательностей будут
располагаться в строках с номерами s и t согласно формуле (4).
Тогда алгоритм работы процессора дискретного преобразования (рис.1) будет описываться следующим математическим выражением:
где 
-
матрица размера 
, состоящая из пар дополнительных
последовательностей длины
N, упорядоченная в соответствии с (6).
Далее будем называть эту матрицу матрицей Д-последовательностей порядка k, а выражение (7) – дискретным Д-преобразованием
(ДП-Д).
Матрицу Д-последовательностей можно представить в виде произведения слабо заполненных матриц, т.е. факторизовать, в соответствии со следующим выражением:
где 
– номер
итерации при факторизации матрицы Д-последовательностей порядка k, 
,
- матрица перестановки,
,
-
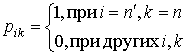номера строк матриц 
и 
соответственно.
Номера строк матриц 
и связаны
в соответствии со следующим выражением:
,
где k – порядок матрицы Д-последовательностей,
-
номер итерации при расчете матрицы ,
,
,
-
операция поразрядного сложения по модулю два,
-
число a по модулю два,
-
число b в двоичном виде.
Матрицы-сомножители 
из выражения (8) можно вычислить, используя алгоритм факторизации Гуда [3]:
где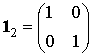 
-
единичная матрица размером 
,
-
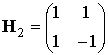матрица Адамара размером ,
-
операция кронекеровского произведения.
Из выражений (7) и (8) следует, что ДП-Д можно преобразовать к виду:
.
(11)
Выражение (11) далее будем называть быстрым Д-преобразованием (БП-Д).
Рассмотрим
алгоритм факторизации матрицы Д-последовательностей порядка k (8) на примере при 
. В
этом случае согласно (8) и (9) получим следующие выражения:
Рассмотрим первую
итерацию. При 
из (9) следует, что:
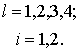
Из (12) следует, что:
.
.
Из (12) следует, что:
Из (12) следует, что:
Из (12) следует, что:
В таблице 2 представлено полученное
соответствие номеров строк матрицы 
номерам строк матрицы 
.
Таблица 2.
|
|
|
|
1 |
1 |
|
2 |
2 |
|
3 |
7 |
|
4 |
8 |
|
5 |
5 |
|
6 |
6 |
|
7 |
3 |
|
8 |
4 |
Из (8) и таблицы 2 следует, что для первой итерации матрица перестановки будет иметь следующий вид:
.
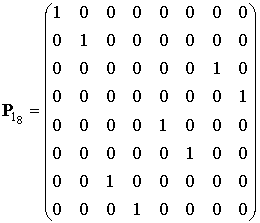Тогда согласно (12) для первой итерации получим:
(13)
(матрица 
получена
согласно алгоритму факторизации Гуда (10) при ).
Рассмотрим
вторую итерацию. При 
из (9) следует, что:
Выполняя расчеты,
аналогичные выполненным для первой итерации, получим таблицу 3 соответствия номеров
строк матрицы 
номерам строк матрицы 
.
Таблица 3.
|
|
|
|
1 |
1 |
|
2 |
4 |
|
3 |
3 |
|
4 |
2 |
|
5 |
5 |
|
6 |
8 |
|
7 |
7 |
|
8 |
6 |
Из (8) и таблицы 3 следует, что для второй итерации матрица перестановки будет иметь следующий вид:
.
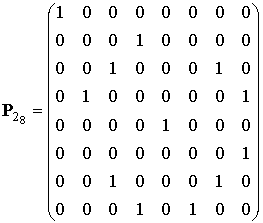Тогда согласно (12) для второй итерации получим:
(14)
(матрица получена
согласно алгоритму факторизации Гуда (10) при ).
Из (12), (13) и (14) следует, что:
(15)
(матрица 
получена
согласно алгоритму факторизации Гуда (10) при ).
Из (15) следует, что в
результате произведения всех слабо заполненных матриц, входящих в алгоритм
факторизации (8) при , получена матрица Д-последовательностей
3-го порядка. Это подтверждает правильность данного алгоритма при любом k. Также из (15) видно, что пары дополнительных
последовательностей располагаются в строках согласно формуле (4): 1 и 5, 2 и 6,
3 и 7, 4 и 8.
Далее
построим сигнальный граф
БП-Д (11) при , используя полученные выше матрицы-сомножители (13), (14) и (15):
.
Пусть вектор входного сигнала имеет вид:
.
Тогда в результате выполнения первой итерации БП-Д получим вектор:
.
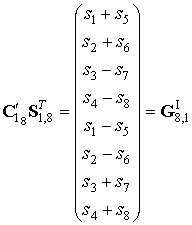Результатом выполнения второй итерации является вектор:
.
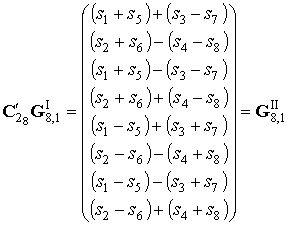В результате выполнения третьей итерации получим искомый вектор спектра дискретного Д-преобразования:
.
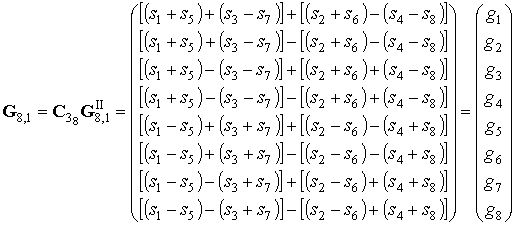Сигнальный
граф быстрого
Д-преобразования при представлен на рис.2.
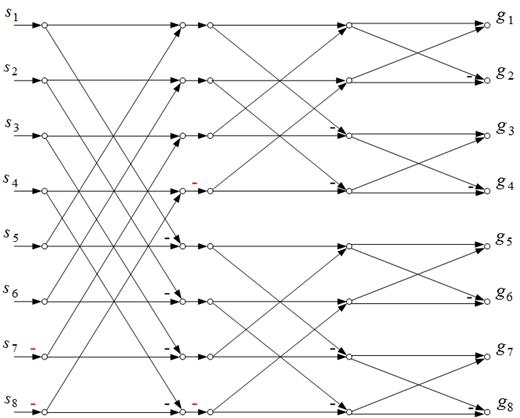
Рис.2. Сигнальный
граф БП-Д при
Из
рис.2 видно, что граф БП-Д представляет собой граф быстрого преобразования
Уолша-Адамара (БПУ) с упорядочением по Адамару [3] с добавлением с первой по 
-ю итерации дополнительных вещественных весовых
коэффициентов «-1» (на рис.2 выделены красным цветом).
Определим «блоком» группу сложений и вычитаний, которая не связана с соседними группами, расположенными как выше, так и ниже. Тогда в общем случае при любом k количество дополнительных весовых коэффициентов в каждом блоке итерации определяется формулой:
,
(16)
где k – порядок матрицы Д-последовательностей (число итераций БП-Д);
j – номер итерации.
Дискретное Д-преобразование (7) имеет:
алгебраических операций сложения-вычитания
типа 
, а быстрое Д-преобразованием, как и БПУ, имеет:
операций сложения-вычитания.
При больших N 
. Т.о.,
выигрыш в числе алгебраических операций при вычислении спектра по алгоритму
БП-Д относительно вычислений по алгоритму ДП-Д составит:
. (17)
Выводы
Структурная схема устройства сжатия когерентных дополнительных сигналов представляет собой эквивалентную структурную схему согласованного фильтра. Алгоритм работы данной эквивалентной схемы включает в свой состав быстрое Д-преобразование, представляющее собой быстрое преобразование Уолша-Адамара с добавлением с первой по предпоследнюю итерации дополнительных вещественных весовых коэффициентов. Это позволяет эффективно в реальном масштабе времени решать задачи разрешения и измерения координат групповых радиолокационных целей с близкими радиальными скоростями.
Литература
1. Р.Н. Ипанов. Когерентные дополнительные сигналы и их применение в радиолокации. // Журнал радиоэлектроники: электронный журнал. 2015. №2. URL: http://jre.cplire.ru/jre/feb15/8/text.pdf
2. Велти. Четверичные коды для импульсного радиолокатора. // Зарубежная радиотехника. 1961, №4, с. 3-19.
3. Трахтман А.М., Трахтман В.А. Основы теории дискретных сигналов на конечных интервалах. М.: Сов. радио, 1975, 208 с.