| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 7, 2001 |
|
ЭКВИВАЛЕНТНЫЙ ПУТЬ РАСПРОСТРАНЕНИЯ ДЕКАМЕТРОВОЙ ВОЛНЫ В СФЕРИЧЕСКИСЛОИСТОЙ ИОНОСФЕРЕ
В. П. Пашинцев, С. А. Тишкин, А. А. Смирнов, И. И. Боровлев
Филиал Ростовского военного института ракетных войск
Получена 16 июля 2001 г.
Разработана аналитическая методика определения группового, фазового и реального путей декаметровой волны в сферическислоистой ионосфере, на основе которой получено выражение для расчета эквивалентного пути распространения этой волны.
Известно [1], что характеристики замираний
принимаемого сигнала в декаметровом (ДКМ) диапазоне при приходе единичной
отраженной волны определяются дисперсией флуктуаций ее фазового фронта (![]() ) на выходе
ионосферного слоя F с
пространственными неоднородностями электронной концентрации (ЭК). Выражение для
расчета
) на выходе
ионосферного слоя F с
пространственными неоднородностями электронной концентрации (ЭК). Выражение для
расчета
![]() получено
благодаря введенному понятию эквивалентного пути (
получено
благодаря введенному понятию эквивалентного пути (![]() ) распространения ДКМ волны в
ионосферной "трубке" с однородной ЭК, соответствующей высоте (
) распространения ДКМ волны в
ионосферной "трубке" с однородной ЭК, соответствующей высоте (![]() ) отражения
волны
) отражения
волны
![]() .
При этом величина
.
При этом величина
![]() определяется из выражения для полного
количества электронов
определяется из выражения для полного
количества электронов
![]() в "трубке" сечением 1
в "трубке" сечением 1
![]() вдоль
реального пути
вдоль
реального пути
![]() в ионосферном слое F
с неоднородной по высоте ЭК
в ионосферном слое F
с неоднородной по высоте ЭК
![]() :
:
где
![]() –
элементарный участок
–
элементарный участок
![]() ;
;
![]() - усредненное вдоль реального пути (т. е.
однородное) значение ЭК в ионосферной "трубке", причем
- усредненное вдоль реального пути (т. е.
однородное) значение ЭК в ионосферной "трубке", причем
![]() <
<![]() , а
, а
![]() . Однако полученное
в [1] выражение для
. Однако полученное
в [1] выражение для
![]() неудобно для инженерных расчетов,
поскольку учитывает влияние сферичности Земли и ионосферы через традиционный
поправочный коэффициент (
неудобно для инженерных расчетов,
поскольку учитывает влияние сферичности Земли и ионосферы через традиционный
поправочный коэффициент (![]() ), вычисляемый приближенно.
), вычисляемый приближенно.
Целью статьи является разработка аналитического метода расчета эквивалентного пути распространения ДКМ волны в отражающем слое F с учетом сферичности Земли и ионосферы.
1. ОБОСНОВАНИЕ ПОДХОДА К РЕШЕНИЮ ЗАДАЧИ
Геометрия распространения ДКМ волны с рабочей частотой
![]() при
ее падении под углом
при
ее падении под углом
![]() на нижнюю границу
на нижнюю границу
![]() сферическислоистой
ионосферы (т.е. с учетом влияния кривизны Земли и ионосферного отражающего слоя
F ) показана на рис. 1.
сферическислоистой
ионосферы (т.е. с учетом влияния кривизны Земли и ионосферного отражающего слоя
F ) показана на рис. 1.
С ростом высоты (![]() ) ЭК ионосферы
) ЭК ионосферы
![]() в
элементарных сферических слоях возрастает до значения
в
элементарных сферических слоях возрастает до значения ![]() , соответствующего
высоте
, соответствующего
высоте ![]() максимума
ионизации. При этом коэффициент преломления ионосферы уменьшается согласно
выражению [2-5]
максимума
ионизации. При этом коэффициент преломления ионосферы уменьшается согласно
выражению [2-5]
где e и
![]() - заряд и масса электрона;
- заряд и масса электрона;
![]() -
диэлектрическая проницаемость вакуума; коэффициент
-
диэлектрическая проницаемость вакуума; коэффициент
![]() имеет в системе СИ
размерность [
имеет в системе СИ
размерность [![]() ], а
], а
![]() - плазменная частота ионосферы
[Гц] на высоте h.
- плазменная частота ионосферы
[Гц] на высоте h.
Согласно закону Снеллиуса, для любой высоты h сферическислоистой ионосферы (рис. 1) справедливо равенство [3-5]
где
![]() км – радиус Земли;
км – радиус Земли;
![]() - текущий угол наклона
траектории распространения ДКМ волны.
- текущий угол наклона
траектории распространения ДКМ волны.
Из (2, 3) следуют условие отражения ДКМ волны (в точке
B, где
![]() ) и соотношение для
выбора ее рабочей частоты [3, 4]:
) и соотношение для
выбора ее рабочей частоты [3, 4]:
где ![]() - частота вертикально направленной волны,
эквивалентной
- частота вертикально направленной волны,
эквивалентной
![]() ;
;
![]() - высота точки отражения над нижней
границей ионосферы;
- высота точки отражения над нижней
границей ионосферы;
![]() - поправочный коэффициент, учитывающий
кривизну Земли и ионосферы.
- поправочный коэффициент, учитывающий
кривизну Земли и ионосферы.
Примерное равенство (5) справедливо при
![]() . При более
жестком условии
. При более
жестком условии
![]() можно воспользоваться разложением в биномиальный
ряд
можно воспользоваться разложением в биномиальный
ряд
![]() и
записать (4) и (5) в виде:
и
записать (4) и (5) в виде:
Известен [1] подход к определению
![]() из соотношения (1),
согласно которому
из соотношения (1),
согласно которому
В соответствии с (2, 7) отношение
![]() связано с
связано с
![]() как
как
![]() .
.
Выражая отсюда указанное отношение и подставляя его в (8), получим
где реальный путь ДКМ волны в ионосфере
![]() и квадрат
усредненного вдоль
и квадрат
усредненного вдоль
![]() значения коэффициента преломления
ионосферы
значения коэффициента преломления
ионосферы
![]() определяются
как
определяются
как
Входящие в (9) значения
![]() и
и
![]() можно определить с помощью
известных [2, 4] выражений для фазового (
можно определить с помощью
известных [2, 4] выражений для фазового (![]() ) и группового (
) и группового (![]() ) путей распространения
волны в ионосфере, представляемых в виде [1]
) путей распространения
волны в ионосфере, представляемых в виде [1]
Отсюда имеем
и выражение (9) сводится к виду
Таким образом, для расчета эквивалентного пути
распространения ДКМ волны в сферическислоистой ионосфере (14) необходимо
получить аналитические выражения для определения ее реального, фазового и
группового путей, связанных между собой согласно (10 -
12) соотношениями
![]() .
.
2. ОПРЕДЕЛЕНИЕ ГРУППОВОГО И ФАЗОВОГО ПУТЕЙ РАСПРОСТРАНЕНИЯ ДЕКАМЕТРОВОЙ ВОЛНЫ В СФЕРИЧЕСКИСЛОИСТОЙ ИОНОСФЕРЕ
В приведенных общих выражениях (10 -
12) для
![]() элемент
реального пути dl
связан с элементом высоты dh
траектории распространения волны и текущим углом ее наклона
элемент
реального пути dl
связан с элементом высоты dh
траектории распространения волны и текущим углом ее наклона
![]() соотношением [2,
4]
соотношением [2,
4]
Для сферическислоистой ионосферы
![]() выражается из (3) как
выражается из (3) как
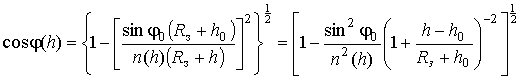 .
.
Поскольку
![]() , то
, то
![]() и последнее выражение можно
записать в виде
и последнее выражение можно
записать в виде
В соответствии с рис.1 реальная траектория
распространения ДКМ волны по пути ABC
протяженностью
![]() симметрична относительно точки B с высотой
симметрична относительно точки B с высотой
![]() . Поэтому общие выражения (10 –
12) для
путей распространения ДКМ волны в сферическислоистой ионосфере принимают согласно
(15) и (16) следующий вид:
. Поэтому общие выражения (10 –
12) для
путей распространения ДКМ волны в сферическислоистой ионосфере принимают согласно
(15) и (16) следующий вид:
Чтобы получить аналитические выражения для определения
этих путей, конкретизируем
![]() для параболической модели распределения
по высоте ЭК в ионосферном слое
для параболической модели распределения
по высоте ЭК в ионосферном слое
![]()
где
![]() - полутолщина слоя. Подстановка (20) в
(2) дает [4,5]
- полутолщина слоя. Подстановка (20) в
(2) дает [4,5]
где
![]() - критическая частота ионосферы.
- критическая частота ионосферы.
В настоящее время известны [5, 6] аналитические методики определения группового, фазового, реального и эквивалентного путей ДКМ волны в плоскослоистом ионосферном слое с параболическим распределением ЭК (20). Обобщим эти методики на случай сферическислоистой ионосферы.
Подставив (21) в (19) и произведя замену переменной (![]() ), получим
), получим
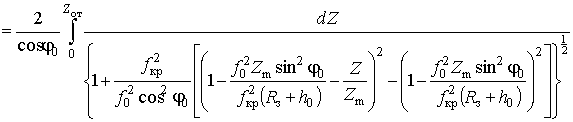 . (22)
. (22)
Введя обозначения
выражение (22) можно свести к виду
Далее путем подстановки (21) при
![]() в (6), можно получить
равенство
в (6), можно получить
равенство
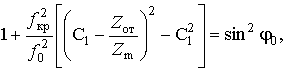
из которого следует
Последнее равенство позволяет записать (24) в виде
где
Тогда, используя табличный интеграл [7]
выражение (26) для группового пути распространения волн в сферически- плоской ионосфере можно представить в аналитическом виде
где
Достоверность полученных выражений (29,
30)
подтверждается тем, что в частном случае плоскослоистой ионосферы (![]() ) значение
) значение
![]() и (29)
сводится к известному виду [5]
и (29)
сводится к известному виду [5]
где в соответствии с (7)
![]() , т. к.
, т. к.
![]() .
.
Сравнительный анализ полученных выражений (29,
30) с
известным (31) показывает, что сферическая ионосфера влияет на
![]() подобно
плоскослоистой, у которой
подобно
плоскослоистой, у которой
![]() понижена до значения
понижена до значения
![]() . Поэтому в плоскослоистой
ионосфере (
. Поэтому в плоскослоистой
ионосфере (![]() )
значение
)
значение
![]() при
отношении
при
отношении
![]() ,
а в сферическислоистой ионосфере
,
а в сферическислоистой ионосфере
![]() при отношении
при отношении
![]() , причем
, причем
![]() уменьшается
относительно единицы при увеличении
уменьшается
относительно единицы при увеличении
![]() .
.
Следовательно, в сферическислоистой ионосфере (![]() ) значение
) значение
![]() будет больше,
чем в плоскослоистой (
будет больше,
чем в плоскослоистой (![]() ) при одном и том же отношении
) при одном и том же отношении
![]() .
.
Применяя аналогичный способ подстановки (21) в (18), выражение для фазового пути распространения ДКМ волны в сферическислоистой ионосфере можно получить в виде
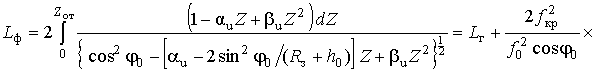
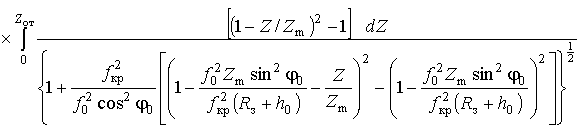 ,
,
где
![]() определяется согласно (22).
определяется согласно (22).
С учетом обозначений (23) это выражение сводится к виду
Поскольку
![]() ,
,
то выражение (32) с учетом (24) представляется четырьмя слагаемыми
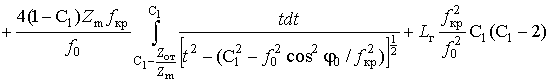 . (33)
. (33)
Тогда с учетом равенства (25) и обозначения (27) выражение (33) принимает вид
Такое представление позволяет воспользоваться табличными интегралами [7]
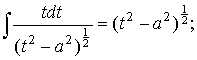
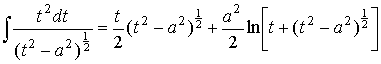
и привести (34) к виду
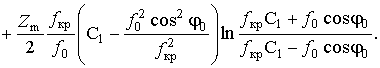 (35)
(35)
Поскольку последнее слагаемое (35) можно выразить
через
![]() (29),
то в аналитическом виде фазовый путь распространения ДКМ волны в
сферическислоистой ионосфере определяется как
(29),
то в аналитическом виде фазовый путь распространения ДКМ волны в
сферическислоистой ионосфере определяется как
где
![]() определяется согласно (30). Достоверность
(36) подтверждается тем, что в частном случае плоскослоистой ионосферы (
определяется согласно (30). Достоверность
(36) подтверждается тем, что в частном случае плоскослоистой ионосферы (![]() ) оно
сводиться к известному [6] виду. Сравнительный анализ полученных выражений (29,
36) показывает, что значение
) оно
сводиться к известному [6] виду. Сравнительный анализ полученных выражений (29,
36) показывает, что значение
![]() .
.
3. ОПРЕДЕЛЕНИЕ РЕАЛЬНОГО И ЭКВИВАЛЕНТНОГО ПУТИ РАСПРОСТРАНЕНИЯ ДЕКАМЕТРОВОЙ ВОЛНЫ В СФЕРИЧЕСКИСЛОИСТОЙ ИОНОСФЕРЕ
Получить удобное аналитическое выражение для расчета
реального пути (![]() ) аналогичным способом прямой подстановки
(21) в (17) не удастся. Однако при выборе рабочих частот (7), удовлетворяющих
условию
) аналогичным способом прямой подстановки
(21) в (17) не удастся. Однако при выборе рабочих частот (7), удовлетворяющих
условию
выражение (2) можно разложить в биномиальный ряд
обеспечивая в расчетах два точных десятичных знака
[8]. Условие (37) справедливости разложения (38) выполняется для достаточно
пологих траекторий распространения ДКМ волны (![]() , что соответствует при отражении
от слоя F2 дальности связи
, что соответствует при отражении
от слоя F2 дальности связи
![]() км [4]). В
этих случаях примерное равенство (38) можно записать в виде
км [4]). В
этих случаях примерное равенство (38) можно записать в виде
В соответствии с (39) реальный путь
![]() (17)
распространения ДКМ волны в сферическислоистой ионосфере можно найти через
групповой
(17)
распространения ДКМ волны в сферическислоистой ионосфере можно найти через
групповой
![]() (19)
и фазовый
(19)
и фазовый![]() (18) пути как
(18) пути как
Подстановка в (40) выражения для
![]() (36) позволяет
получить аналитическое выражение для реального пути через групповой путь (29) в
виде
(36) позволяет
получить аналитическое выражение для реального пути через групповой путь (29) в
виде
В частном случае
![]() выражение (41) сводиться к
известному виду [6].
выражение (41) сводиться к
известному виду [6].
Сравнительный анализ полученных выражений (29,
36, 41)
указывает на выполнение соотношений
![]() . Достоверность указанных выражений
подтверждается тем, что при выполнении условия (37) справедливости разложения
(38) отличия значений
. Достоверность указанных выражений
подтверждается тем, что при выполнении условия (37) справедливости разложения
(38) отличия значений ![]() будут иметь одинаковую величину и
противоположный знак [2]:
будут иметь одинаковую величину и
противоположный знак [2]:
При этом значения поправок на групповой (![]() ) и фазовый (
) и фазовый (![]() ) пути
распространения ДКМ волны в сферическислоистой ионосфере определяются как
) пути
распространения ДКМ волны в сферическислоистой ионосфере определяются как
Поэтому выражения для
![]() (41) и
(41) и
![]() (36) можно записать в
виде
(36) можно записать в
виде
где
![]() определяются согласно (29) и (43).
определяются согласно (29) и (43).
Найденные выражения для
![]() (36,
44) позволяют определить
согласно (13) квадрат усредненного коэффициента преломления сферическислоистой
ионосферы вдоль реального пути
(36,
44) позволяют определить
согласно (13) квадрат усредненного коэффициента преломления сферическислоистой
ионосферы вдоль реального пути
![]() распространения ДКМ волны
распространения ДКМ волны
Достоверность полученного выражения (45)
подтверждается тем, что в частном случае плоскослоистой ионосферы (![]() ) оно сводится
к известному виду [1].
) оно сводится
к известному виду [1].
Подставив (45) в (9, 14), получим выражение для эквивалентного пути ДКМ волны в виде
где
![]() определяются согласно (41) и (7).
определяются согласно (41) и (7).
Данное выражение неудобно для расчетов, поскольку
поправочный коэффициент
![]() на сферичность Земли и ионосферы зависит
от высоты отражения
на сферичность Земли и ионосферы зависит
от высоты отражения
![]() и на практике вычисляется приближенно
[4]. При этом величина
и на практике вычисляется приближенно
[4]. При этом величина
![]() может быть определена только, если
известен закон высотного распределения N(h). Для параболической модели
распределения ЭК (20) значение
может быть определена только, если
известен закон высотного распределения N(h). Для параболической модели
распределения ЭК (20) значение
![]() определяется из равенства (25) как
определяется из равенства (25) как
Тогда значение
![]() можно рассчитать согласно выражению
можно рассчитать согласно выражению
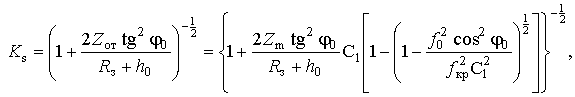
или с учетом взаимосвязи
![]() (30) с
(30) с
![]() как
как
Подставив (48) в (46), получим искомое выражение для
расчета эквивалентного пути (![]() ) распространения ДКМ волны в
сферическислоистой ионосфере
) распространения ДКМ волны в
сферическислоистой ионосфере
Достоверность (49) подтверждается тем, что в частном
случае плоскослоистой ионосферы (![]() ) оно сводится к известному [6] виду.
) оно сводится к известному [6] виду.
Анализ (49) показывает следующее. При малых отношениях
![]() ,
когда справедливо разложение
,
когда справедливо разложение
![]() при обеспечении в расчетах двух точных
десятичных знаков [8], согласно (29) будем иметь
при обеспечении в расчетах двух точных
десятичных знаков [8], согласно (29) будем иметь
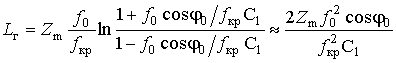
и второй сомножитель числителя (49) равен 1. Поскольку
в этом случае знаменатель (т.е.
![]() ) близок к 1, то
) близок к 1, то
![]() . При наибольших
отношениях
. При наибольших
отношениях
![]() когда
когда
![]() ,
второй сомножитель числителя (49) стремится к
,
второй сомножитель числителя (49) стремится к
![]() , знаменатель – к
, знаменатель – к
![]() (т.е.
(т.е.
![]() ) и
) и
![]() .
.
ЗАКЛЮЧЕНИЕ
Разработана методика, позволяющая получить аналитические выражения для определения группового (29), фазового (36) и реального (41) путей распространения ДКМ волны в сферическислоистом отражающем слое ионосферы с параболическим распределением ЭК и на их основе рассчитать эквивалентный (49) путь этой волны.
СПИСОК ЛИТЕРАТУРЫ
1. Пашинцев В.П., Колосов Л.В., Тишкин С.А., Антонов В.В. // РЭ. 1996. Т41. №1. С. 26.
2. Колосов А.А., Арманд Н.А., Яковлев О.И. Распространение радиоволн при космической связи. М.: Связь, 1969.
3. Черенкова Е.Л., Чернышев О.В. Распространение радиоволн. М.: Радио и связь, 1984.
4. Калинин А.И., Черенкова Е.Л. Распространение радиоволн и работа радиолиний. М.: Связь, 1971.
5. Дэвис К. Радиоволны в ионосфере. М.: Мир, 1973.
6. Пашинцев В. П., Тишкин С. А., Солчатов М. Э. // Журнал радиоэлектроники. 2001. № 6. http://jre.cplire.ru/jre/jun01/3/text.html
7. Выгодский М.Я. Справочник по высшей математике. М.: Наука, 1969.
8. Брадис В.М. Четырехзначные математические таблицы. М.: Учпедгиз, 1962.
Авторы:
Пашинцев Владимир Петрович (vladimir_petrovic@mail.ru), Тишкин Сергей Алексеевич, Смирнов Александр Александрович (shursun@mail.ru), Боровлев Игорь Иванович
Филиал Ростовского военного института ракетных войск
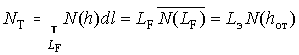 , (1)
, (1)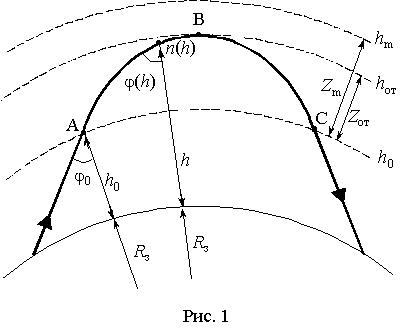
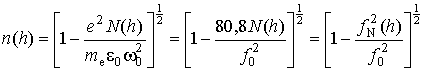 ,
(2)
,
(2)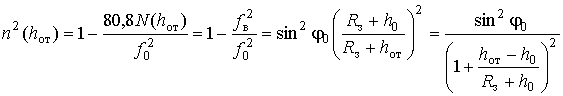 ; (4)
; (4)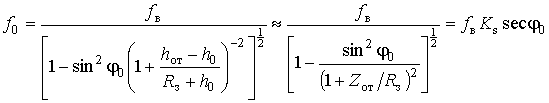 , (5)
, (5)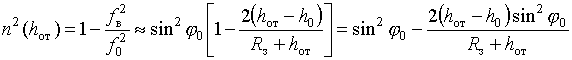 ; (6)
; (6)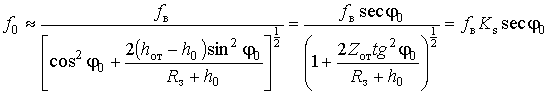 . (7)
. (7)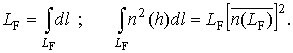 (10)
(10)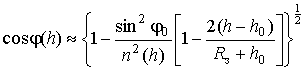 . (16)
. (16)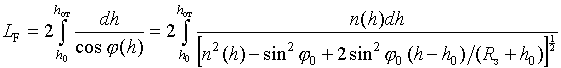
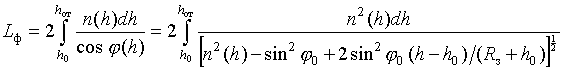
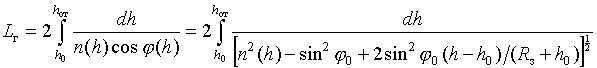
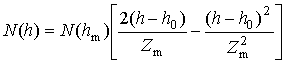
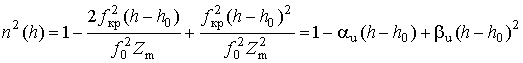 , (21)
, (21)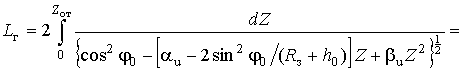
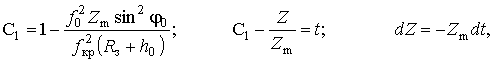
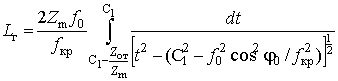 .
(24)
.
(24)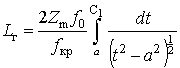 ,
(26)
,
(26)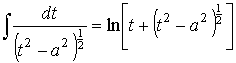 ,
(28)
,
(28)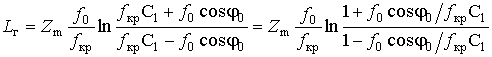 , (29)
, (29)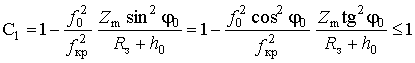
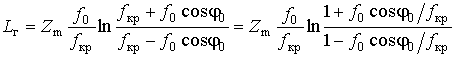 , (31)
, (31)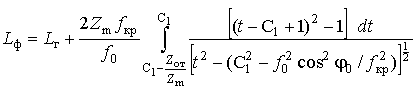 . (32)
. (32)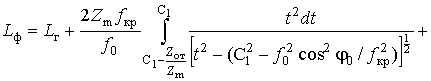
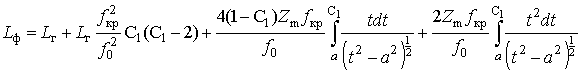 . (34)
. (34)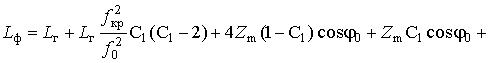
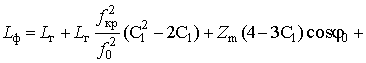
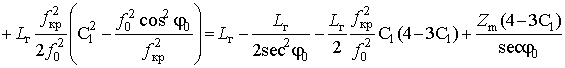 , (36)
, (36)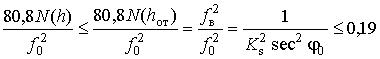 , (37)
, (37)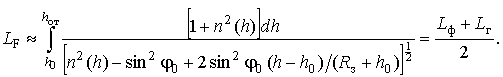 (40)
(40)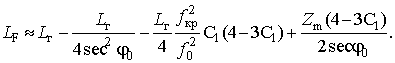 (41)
(41)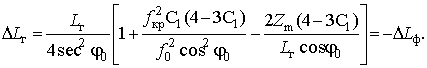 (43)
(43)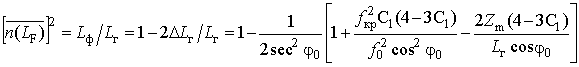 . (45)
. (45)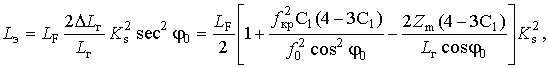 (46)
(46)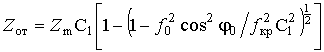 . (47)
. (47)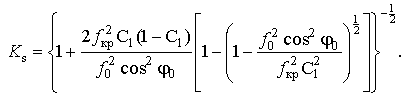 (48)
(48)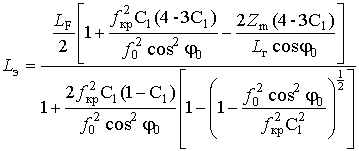 . (49)
. (49)