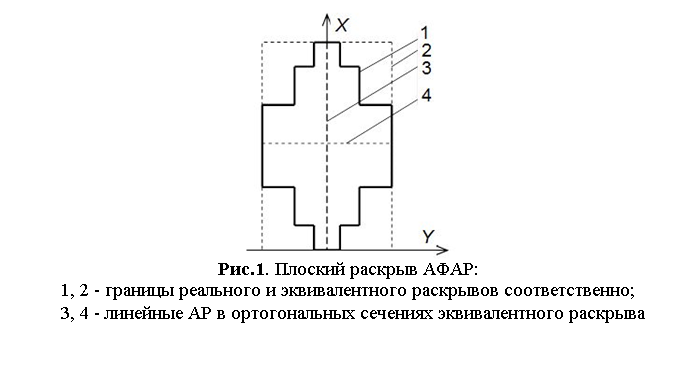
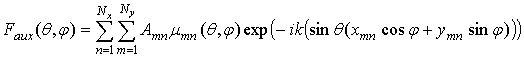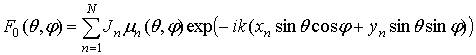УДК 621.396.677

ФОРМИРОВАНИЕ ДИАГРАММЫ НАПРАВЛЕННОСТИ ПЛОСКОЙ АКТИВНОЙ ФАЗИРОВАННОЙ АНТЕННОЙ РЕШЕТКИ

С ПРОИЗВОЛЬНОЙ ГРАНИЦЕЙ РАСКРЫВА

 

Д. Д. Габриэльян¹, М. Ю. Звездина², И. Г. Цыпорина², В. В. Шацкий¹, Н.В. Шацкий³

¹ФГУП «Федеральный научно-производственный центр РНИИРС»,

² Кафедра «Радиоэлектроника» Ростовского технологического института сервиса и туризма (филиал) ФГБОУ ВПО «Южно-Российский государственный университет экономики и сервиса» ³Секция прикладных проблем при Президиуме РАН (Северо-Кавказское отделение), г. Ростов-на-Дону

 

Получена 25 сентября 2012 г., после доработки - 28 ноября 2012 г.

 

Аннотация. Рассматривается плоская активная фазированная антенная решетка (АФАР), имеющая раскрыв с произвольной формой границы. Описаны метод формирования диаграммы направленности АФАР с низким уровнем бокового излучения и устройство, реализующее метод. Результаты моделирования демонстрируют эффективность данного подхода.

Ключевые слова: активная фазированная антенная решетка, диаграмма направленности, произвольная граница раскрыва, эквивалентный плоский раскрыв.

Abstract. Plane active phased antenna array with arbitrary aperture boundary is considered. A low fringe radiation beam forming method for active phased antenna arrays and a device implementing the abovementioned method are described. Simulation results demonstrate the approach efficiency.

Keywords: active phased antenna array, directivity pattern, arbitrary aperture boundary, equivalent flat aperture.

 

Введение.

В последнее время в связи с созданием многофункциональных радиоэлектронных средств различного назначения и значительным усложнением радиоэлектронной обстановки особую актуальность приобретают вопросы использования и размещения активных фазированных антенных решеток, обеспечивающих решение широкого круга задач на объектах-носителях. Широкое применение находят плоские АФАР, имеющие раскрыв с произвольной формой границы, что обусловлено необходимостью размещения раскрывов различных диапазонов на ограниченном участке поверхности, выделенном для антенных систем. Указанные ситуации возникают при установке антенн на кораблях, автомобилях и т.п. Другой особенностью, связанной с необходимостью работы АФАР в сложной помеховой обстановке, является формирование диаграмм направленности (ДН) с произвольным законом изменения уровня боковых лепестков, в том числе и низким уровнем.

В известной литературе, например, [1-3], как правило, приведены рекомендации по формированию произвольного закона изменения и снижению боковых лепестков для АФАР с канонической формой раскрыва (раскрывов прямоугольной и круглой формы). Для таких раскрывов хорошо изучена взаимосвязь параметров раскрыва (размер раскрыва, закон изменения амплитудного распределения в раскрыве) с шириной главного максимума ДН и законом изменения уровня боковых лепестков. При этом данные закономерности относятся к случаю использования строчно-столбцевого закона управления амплитудно-фазовым распределением (АФР) в раскрывах прямоугольной формы или осесимметричного распределения в круглых раскрывах.

Однако в случае раскрывов с произвольной формой границы использование схемы построения АФАР, реализующей, например, строчно-столбцевой закон управления амплитудно-фазовым распределением, может приводить к неточности установки главного луча, а также к существенному повышению уровня боковых лепестков. Указанные недостатки обусловлены отказом от учёта формы раскрыва при использовании строчно-столбцевого закона управления амплитудно-фазовым распределением. Кроме того, в известной литературе отсутствуют результаты исследований взаимосвязи параметров излучающего раскрыва и формируемой ДН.

В соответствии с отмеченными особенностями формирования АФР физически реализуемые ДН для раскрывов с произвольной формой границы могут быть определены только в главных плоскостях. Данное обстоятельство ограничивает, в свою очередь, использование методов синтеза, рассмотренных в [4, 5].

В связи с изложенным выше целью статьи является рассмотрение алгоритма синтеза амплитудно-фазового распределения для АФАР с произвольной формой границы и разработка схемы АФАР для реализации алгоритма.
 

Постановка задачи.

Одним из путей решения поставленной задачи является представленное в [6] предложение ввести эквивалентный плоский раскрыв с канонической формой границы, в частности, прямоугольный, круглый и т.п., в который наилучшим образом вписывается реальный раскрыв АФАР.

В качестве эквивалентного раскрыва рассмотрим прямоугольный раскрыв. Будем считать, что излучатели в раскрыве АФАР и эквивалентном раскрыве располагаются в узлах регулярной прямоугольной сетки с одинаковыми параметрами. При этом координаты излучателей вспомогательного раскрыва, находящихся внутри контура раскрыва АФАР, совпадают с координатами излучателей АФАР. Геометрия решаемой задачи приведена на рис. 1. Такой выбор эквивалентного раскрыва определяется хорошо исследованной взаимосвязью параметров АФР линейных антенн с характеристиками ДН в главных плоскостях, в частности, с поведением огибающей боковых лепестков при использовании строчно-столбцевого закона управления АФР в прямоугольном раскрыве. При этом поведение огибающей боковых лепестков должно быть определено для двух взаимно ортогональных линеек, образующих эквивалентный прямоугольный раскрыв.

 

Назовём ДН эквивалентного прямоугольного раскрыва вспомогательной. При этом для эквивалентного плоского прямоугольного раскрыва достаточно просто сформировать объемную ДН с заданными законами огибающей боковых лепестков в главных сечениях.
 

Решение задачи синтеза.

Решение задачи синтеза для плоского раскрыва с произвольной формой границы, содержащего N излучателей, при использовании вспомогательной ДН позволит реализовать в главных плоскостях близкий к заданному закон изменения огибающей боковых лепестков в главных сечениях и более низкий уровень боковых лепестков в промежуточных азимутальных сечениях. Обеспечение такого поведения боковых лепестков достигается путем наложения требований на формируемую ДН не в двух, а в большем числе сечений [6].

При данном подходе к решению задачи синтеза на первом этапе по заданным положению главного лепестка и законам огибающей боковых лепестков в главных плоскостях заданной ДН вычисляются (выбираются из заранее насчитанных массивов) амплитудно-фазовые распределения , , , , где ,  - число излучателей в эквивалентных линейках. В качестве линеек выбираются линейные АР максимальной длины, которые могут быть выделены в составе рассматриваемого плоского раскрыва с произвольной формой границы. Алгоритм нахождения  и  описан в [7].

На основе выбранных АФР в указанных ортогональных линейках формируется общее амплитудно-фазовое распределение в раскрыве прямоугольной формы, содержащем  излучателей. Вспомогательная ДН , имеющая в главных плоскостях заданный закон огибающей боковых лепестков, находится как диаграмма, формируемая эквивалентным прямоугольным раскрывом:

,     (1)

где , ,  ‑ соответственно координаты и ДН излучателя, стоящего на пересечении -й строки и -го столбца,  ‑ АФР эквивалентного прямоугольного раскрыва, определяемое в соответствии со строчно-столбцевым законом управления АФР в виде

.                                                                           (2)

Запишем ДН АФАР с плоским -элементным раскрывом, имеющим произвольную форму границы, в виде:

,          (3)

где , ,  ‑ координаты и ДН -го излучателя в составе излучающего раскрыва с произвольной формой границы.

Следует отметить, что ДН излучателей в раскрыве АФАР и вспомогательном раскрыве полагаются одинаковыми.

Для нахождения АФР  в таком раскрыве потребуем совпадения ДН АФАР и вспомогательной ДН в  направлениях

,   ().                                             (4)

В матричной форме условие (4) может быть представлено следующим образом:

.                                                       (5)

Элементы матрицы  системы (5) определяются соотношениями:

,

где  ‑ ДН n–го излучателя в направлении, определяемом углами . Элементами вектора-столбца  являются неизвестные токи в излучателях АФАР, а элементами вектора-столбца  ‑ значения , (, ).

При выполнении условия  получаемое решение системы (5) даёт приближенное решение, являющееся наилучшим в смысле минимизации среднеквадратического отклонения [8] вспомогательной и синтезируемой ДН. Поскольку ранг матрицы  равен , решение задачи амплитудно-фазового синтеза АФАР при этом может быть найдено в виде [8]

,                                                                    (6)

где  ‑ псевдообратная матрица для матрицы , определяемая выражением

 ,                                                               (7)

В выражении (7)  ‑ матрица, транспонированная и комплексно-сопряженная по отношению к матрице.

В частном случае при условии  получаем , и решение (6) принимает вид

.                                                                 (8)

Получаемое в (6) решение обеспечивает минимальное отклонение синтезируемой ДН АФАР с плоским раскрывом, имеющим произвольную форму границы от вспомогательной ДН в среднеквадратическом смысле.
 

Результаты численного моделирования.

Рассмотрим результаты численных исследований точности формирования ДН АФАР, имеющей плоский раскрыв с произвольной формой границы, по отношению к вспомогательной ДН. В качестве критериев рассмотрим такие характеристики, как снижение коэффициента направленного действия (КНД) для раскрыва с формой границы 1 (рис.1) и величину нормированного среднеквадратического отклонения формируемой ДН по отношению к ДН прямоугольного раскрыва 2, определяемое следующим образом

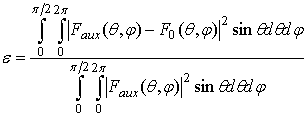.                                                       (9)

Будем полагать, что излучающий раскрыв образован из 384 элементов. Вспомогательная ДН формируется с использованием 480-элементного (40x12) прямоугольного раскрыва. Шаг размещения излучателей во всех случаях вдоль обеих осей равен  (где – рабочая длина волны). Направления, в которых накладываются требования совпадения вспомогательной и синтезируемой ДН, выбираются равномерно по углам  в верхнем полупространстве.

На первом этапе исследований выполним анализ влияния числа направлений , в которых накладывается условие (4) на формирование диаграммы направленности с требуемым законом изменения уровня боковых лепестков в главных плоскостях. Указанные направления будем равномерно выбирать по углу места и углу азимута с одинаковым шагом в пределах полусферы. Выполним исследования при соотношениях ,  и  соответственно. Рассмотрим следующие случаи:

‑ формирование ДН с главным максимумом в направлении нормали к плоскости раскрыва и огибающей, уменьшающейся в сечении  (вдоль большей стороны раскрыва) линейно от  дБ до  дБ и от  дБ до  дБ (по разные стороны от главного максимума), а в сечении  (вдоль меньшей стороны раскрыва) – симметрично по отношению к главному максимуму от  дБ до  дБ;

‑ случай формирования ДН с главным максимумом, отклоненным от направления нормали к плоскости раскрыва на угол  в плоскости , и огибающей линейно уменьшающейся в сечении  от  дБ до  дБ и от  дБ до  дБ (по разные стороны от главного максимума), а в сечении  – симметрично по отношению к главному максимуму от  дБ до  дБ.

Выполненные исследования по оценке взаимосвязи числа направлений  и соответствия уровня боковых лепестков формируемой ДН заданному закону изменения огибающей показали, что в случае  решение задачи амплитудно-фазового синтеза не имеет практического значения, поскольку наблюдается значительное превышение уровня боковых лепестков над заданным уровнем. При выполнении условия  получаемое решение практически сходится. При дальнейшем увеличении  до значения  уровень боковых лепестков формируемых ДН не превышает заданный. Данный вывод остается справедливым и при рассмотрении случаев формирования ДН, огибающие уровней боковых лепестков которых определяются другими параметрами. Таким образом, в дальнейшем решение задачи синтеза проводится при условии .

В табл.1 приведены результаты сравнительного анализа двух алгоритмов синтеза АФР: возбуждение всех элементов раскрыва 1 с учетом формы границы на основе соотношений (3)-(7); возбуждение в пределах раскрыва 1 двух взаимно-ортогональных линеек [9]. Величина КНД для прямоугольного раскрыва соответственно равна 25,55 дБ и 21,85 дБ.

 

Таблица 1. Снижение КНД и среднеквадратическое отклонение вспомогательной и формируемой ДН

Положение главного лепестка ДН	АФАР с раскрывом 1 на рис.1 и синтезированной ДН		АФАР с раскрывом 1 на рис.1 при возбуждении по формуле (2)
	КНД, дБ		КНД, дБ
,	24,87	0,006	23,43	0,012
,	21,37	0,022	18,37	0,166

 

Анализ данных табл.1 показывает, что предлагаемый алгоритм синтеза АФР обеспечивает по сравнению с предлагаемым в работе [9] выигрыш в величине КНД не менее 1,4 дБ при неотклоненном луче главного лепестка ДН и 3 дБ при отклоненном луче. При этом снижение КНД, связанное с отклонением формы излучающего раскрыва от эквивалентной прямоугольной, в которую вписывается реальный раскрыв, не превышает 0,7 дБ при неотклоненном луче и 0,5 дБ при отклоненном на  от нормали к раскрыву луче. Однако наблюдающееся относительно небольшое снижение КНД позволяет уменьшить площадь раскрыва антенны на 25%.

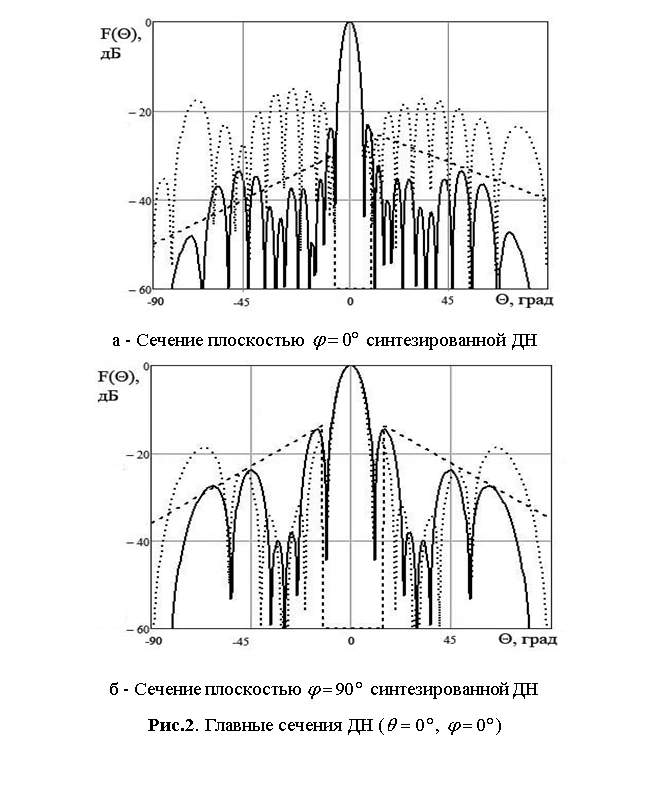
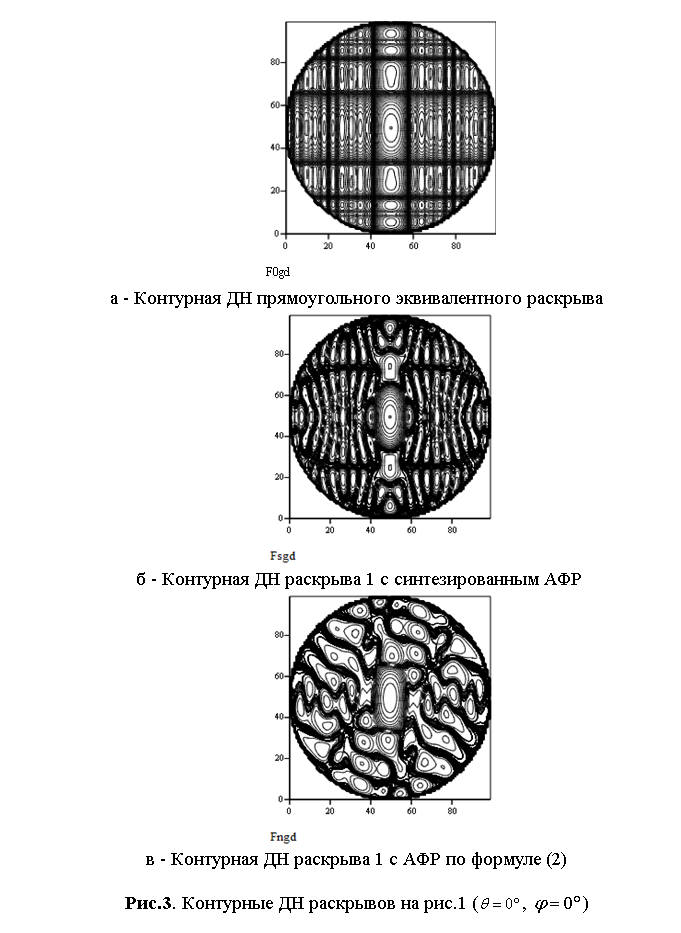
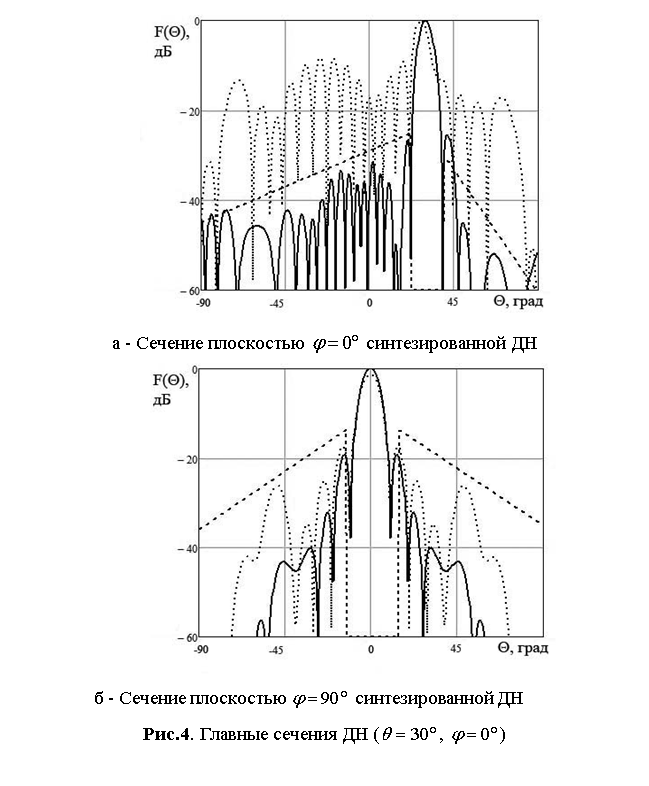
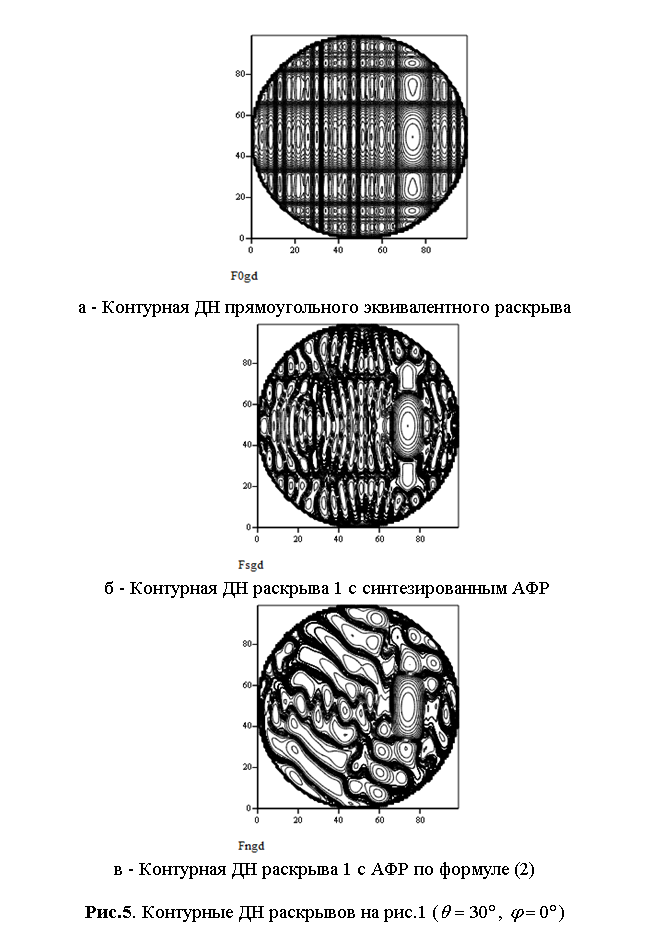
На рис. 2–5 приведены получаемые при использовании предлагаемого алгоритма синтеза АФР сечения ДН в плоскостях  и  (рис. 2), контурные ДН (рис. 3) для неотклонённого луча, сечения диаграмм направленности для  и (рис. 4) и контурные ДН (рис. 5) при отклонении луча от нормали к раскрыву вдоль большей стороны раскрыва на . На рис. 2 и 4 сплошной линией показаны синтезированные ДН, пунктирными линиями ‑ ДН, полученные с использованием выражения (2), как предложено в [9], и штриховыми линиями ‑ заданные огибающие уровня боковых лепестков. При проведении исследований полагалось, что максимальная длина линеек вдоль осей  и  соответственно составляла  и  элементов.

Результаты данных рисунков показывают, что выявленный при анализе табл.1 выигрыш в величине КНД обусловлен тем, что уровень боковых лепестков синтезированной ДН в главных плоскостях практически ниже заданного для всех рассмотренных вариантов огибающей. В диагональном сечении уровень боковых лепестков также не превосходит заданных для главных сечений уровней. Вследствие этого для предложенного метода синтеза ДН АФАР обеспечивается наиболее точное формирование объемной диаграммы направленности с заданными законами изменения огибающей боковых лепестков не только в главных, но и промежуточных сечениях.

 

 

 

 

 

Техническая реализация алгоритма в устройстве обработки сигнала.

На рис.6 показан один из вариантов выполнения структурной схемы устройства, реализующего предлагаемый метод синтеза ДН АФАР, имеющей плоский раскрыв с произвольной формой границы, и формирования объёмной ДН с уровнем лепестков, меньшим заданного.

 

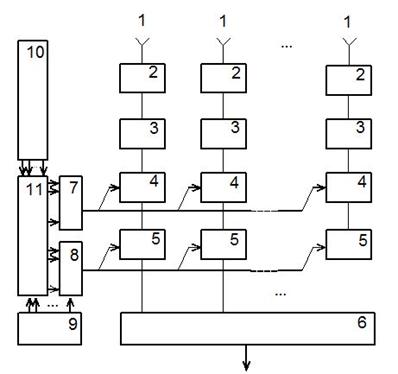
Рис.6. Пример структурной схемы, реализующей предлагаемый метод синтеза

диаграммы направленности:

1 ‑ излучатели; 2 ‑ согласующие цепи; 3 ‑ усилители; 4 ‑ аттенюаторы;

5 ‑ фазовращатели; 6 ‑ распределительное устройство;

7 ‑ блок управления аттенюаторами; 8 ‑ блок управления фазовращателями;

 9 ‑ блок питания; 10 ‑ устройство управления лучом;

11- устройство коррекции

 

В соответствии с данной схемой на первом этапе производится ввод исходных данных. К ним относятся направления формирования максимума ДН  АФАР и заданный закон изменения огибающей уровня боковых лепестков. Указанные данные преобразуются в цифровой код, например, с помощью аналого-цифрового преобразователя, входящего в состав устройства управления лучом 10 (УУЛ). По поступающим командам из него выбираются соответствующие АФР , , ,  для двух взаимно ортогональных линеек (позиции 3, 4 на рис. 1), выбранных из состава плоского раскрыва с произвольной формой границы (позиция 1 на рис. 1) и образующих эквивалентный прямоугольный раскрыв (позиция 2 на рис. 1). Коды, соответствующие двум выбранным АФР, поступают на входы блока формирования АФР эквивалентного прямоугольного раскрыва, входящего в состав УУЛ, где в соответствии с выражением (1) вычисляется АФР  эквивалентного плоского раскрыва. На основе полученных результатов расчёта находится вспомогательная ДН , определяемая с использованием выражения (2), в  направлениях и имеющая заданные параметры (заданный закон огибающей боковых лепестков в главных плоскостях и требуемое значение КНД). Сигналы, соответствующие значениям вспомогательной ДН в  направлениях, поступают с выходов УУЛ на входы устройства коррекции 11 (УК), в котором производится  решение системы линейных алгебраических уравнений (СЛАУ) с использованием хранящихся в памяти коэффициентов псевдообратной матрицы, найденных предварительно с использованием выражения (5) и записанных в память. В УК находится в виде (6) решение задачи амплитудно-фазового синтеза АФАР, имеющей плоский раскрыв с произвольной формой границы. Устройство коррекции обеспечивает минимальное отклонение синтезируемой ДН от вспомогательной ДН в среднеквадратическом смысле. Сигналы, соответствующие значениям полей возбуждения в каналах АФАР, имеющей плоский раскрыв с произвольной формой границы, обрабатываются и происходит выделение действительных и мнимых составляющих полей возбуждения, определение модуля и фазы указанных полей и формирование управляющих воздействий. Сигналы, соответствующие модулям полей возбуждения, поступают на входы блоков 7 управления аттенюаторами, а сигналы, соответствующие фазам полей возбуждения, ‑ на входы блока 8 управления фазовращателями.

Принимаемые излучателями 1 сигналы проходят каналы излучателей, каждый из которых состоит из последовательно включённых излучателя 1, согласующей цепи 2, усилителя 3, аттенюатора 4 и фазовращателя 5. В каналах АФАР с помощью аттенюаторов 4 и фазовращателей 5 устанавливаются необходимые амплитуды и фазы, обеспечивающие формирование синтезированного АФР. Мощность принятых сигналов суммируется в распределительном устройстве 6, выходной сигнал которого соответствует ориентации ДН в направлении  полезного сигнала. Тем самым обеспечивается формирование ДН АФАР, имеющей плоский раскрыв с произвольной формой границы, в требуемом направлении при заданных параметрах (заданном законе огибающей боковых лепестков в главных плоскостях и требуемом значении КНД).

Питание всех блоков и устройств АФАР производится с помощью блока 9 питания. Линии, посредством которых подводится электроэнергия, на рис.4 не показаны, поскольку они практически не отличаются от подобных соединений в известных устройствах.
 

Заключение.

Таким образом, предлагаемый метод синтеза ДН активной фазированной антенной решетки обеспечивает за счет наиболее точного формирования объемной диаграммы направленности с заданными законами изменения огибающей боковых лепестков не только в главных, но и промежуточных сечениях, уменьшение площади раскрыва антенны практически на 25% по сравнению с эквивалентным раскрывом канонической формы. Наблюдаемое при этом снижение величины коэффициента направленного действия не превышает 0,5 дБ даже при отклоненном от нормали луче. Выполнение структурной схемы, реализующей предложенный метод синтеза, не вызывает затруднений и может быть произведена с использованием современной элементной базы.

Литература

1.    Сазонов Д.М. Антенны и устройства СВЧ. М.: Высш. шк. 1988.

2.    Самойленко В.И., Шишов Ю.А. Управление фазированными антенными решётками. М.: Радио и связь, 1983.

3.    Активные фазированные антенные решётки. / Под ред. Д.И. Воскресенского и А.И. Канащенкова. М.: Радиотехника, 2004.

4.     Бахрах Л.Д., Кременецкий С.Д. Синтез излучающих систем. Теория и методы расчета. – М.:Сов. радио, 1974.

5.    Зелкин Е.Г., Соколов В.Г. Методы синтеза антенн: фазированные антенные решетки и антенны с непрерывным раскрывом. – Сов. радио, 1980.

6.    Волошин В.А., Габриэльян Д.Д., Оводов О.В. Синтез амплитудно-фазового распределения в антенных решетках с произвольным контуром //Антенны. 2010. №2(153). С.44-47.

7.    Волошин В.А., Ларин А.Ю., Оводов О.В. Алгоритм синтеза линейных антенных решёток по заданной огибающей боковых лепестков диаграммы направленности //Антенны. 2011. № 12. С. 3-8.

8.    Гантмахер Ф.Р. Теория матриц. М.: Наука. 1967. 575 с.

9.    Стрижков В.А. Направленные свойства и уровень бокового излучения слабовыпуклых фазированных антенных решеток //Антенны. 2007. №1. С. 7-27.