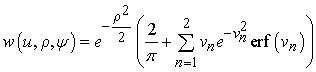ИСПОЛЬЗОВАНИЕ ГРАНИЦЫ ЧЕРНОВА И СТАТИСТИЧЕСКОГО ПРЕДЕЛА РАЗРЕШЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ТОЧНОСТИ ОЦЕНКИ ПАРАМЕТРОВ РАДИОГОЛОГРАФИЧЕСКИХ ОБЪЕКТОВ МИНИМАЛЬНО-ФАЗОВЫМ МЕТОДОМ И ПОСТРОЕНИЯ КЛАССИФИКАЦИОННОЙ СЕТКИ ЭТАЛОНОВ МЕТОДА [1]
А. С. Гвоздарёв, Т. К. Артёмова, К. С. Артёмов
Ярославский государственный университет им. П.Г. Демидова
Получена 11 декабря 2012 г.
Аннотация. В работе рассматривается задача построения сетки эталонов минимально-фазового метода (МФМ) применительно к задачам радиоголографии. В качестве критерия для выбора минимального значения шага сетки использовались: величина статистического предела разрешения (СПР) и допустимые вероятности правильной и ложной классификации. Получены и проанализированы оценки шага сетки в форме границы Рао-Крамера (для СПР) для случая как наличия, так и отсутствия мешающих параметров, и границы Чернова (для вероятностей). Исследованы зависимости полученных оценок от отношения сигнал/шум, объема статистической выборки и величины оцениваемого параметра. Полученные характеристики могут использоваться для определения необходимого объёма выборки при фиксированной эталонной сетке или для формирования эталонной сетки при заданном объёме выборки для обеспечения требуемых вероятностей правильной и ложной классификации. На основе полученных характеристик можно выдать рекомендации к процессу проектирования систем, использующих МФМ.
Ключевые слова: оценка параметров, система голографического радиовидения, эталонный метод, граница Чернова, статистический предел разрешения.
Abstract. Minimum-phase reference method for objects’ dimensions estimation is analyzed. Reference set parameter minimal step is selected in accordance with two criteria: the constrains on acceptable probabilities of detection or total error and the magnitude of the statistical resolution limit. In case of the statistical resolution limit criterion the scalar and vector Cramer-Rao lower bound for minimal-phase method is obtained and analyzed. For the detection and total error probabilities Chernoff inequality constraint is assumed. The method’s accuracy dependence on signal-to-noise ratio, sample size and the estimated parameter value are derived and analyzed. Guidelines for holographic system exploiting minimum-phase method design process are proposed.
Key words: parameter estimation, radioholographic system, reference set method, Chernoff bound, statistical resolution limit.
Введение
Основными задачами, возникающими при использовании эталонных методов, например, [1] оценки параметров наблюдаемых объектов в системах голографического радиовидения (СГРВ) являются задачи, связанные с построением сетки эталонов, и в частности – задача выбора минимального шага сетки, однозначно определяющего точность оценки. На практике при наличии шумов и помех точность оценки, обеспечиваемая эталонными методами на основе выборки из Nstat измерений, ограничена сверху, а шаг сетки эталонов, как следствие, ограничен снизу, и приходится искать разумный компромисс между точностью оценки, обеспечиваемой выбранным набором эталонов, и связкой быстродействие/объём хранимых данных.
Для решения этой задачи в работе применительно к минимально-фазовому методу (МФМ) [2] рассматриваются два подхода: первый – использование в качестве минимального шага сетки эталонов величины статистического предела разрешения (СПР) [3] СРГВ и второй – выбор шага сетки на основе ограничения снизу (сверху) вероятности правильной классификации (полной ошибки классификации) двух соседних эталонов. Под вероятностью правильной классификации PD будем подразумевать полную вероятность (в серии из Nstat испытаний с одинаковыми условиями) того, что система классификации примет решение о равенстве значения оцениваемого параметра исследуемого объекта и эталона, выбранного для сравнения. Под вероятностью ошибочной классификации Pε будем подразумевать сумму вероятности ошибочной классификации (система принимает решение о равенстве оцениваемого параметра у объекта и выбранного эталона при их исходном различии), и пропуска классификации (система не принимает решения о равенстве оцениваемого параметра объекта и выбранного эталона при их исходном совпадении).
Целью работы является определение минимального шага сетки эталонов (который соответствует удвоенной ошибке оценки параметров радиоголографических объектов в СГРВ и удобен для определения точности оценки) минимально-фазового эталонного метода с использованием границы Чернова и статистического предела разрешения.
Математическая модель минимально-фазового метода
Пусть
приёмная часть СРГВ регистрирует поле ![]() , рассеянное исследуемым
объектом с оцениваемым параметром R,
в присутствии комплексного аддитивного белого гауссового шума с дисперсией
, рассеянное исследуемым
объектом с оцениваемым параметром R,
в присутствии комплексного аддитивного белого гауссового шума с дисперсией ![]()
![]() . Пусть так же заранее
сформирована база эталонов
. Пусть так же заранее
сформирована база эталонов 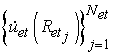 .
В МФМ в качестве оценки
.
В МФМ в качестве оценки ![]() интересующего
параметра исследуемого объекта выбирается значение
интересующего
параметра исследуемого объекта выбирается значение ![]() этого параметра того
эталона, для которого достигается минимум величины
этого параметра того
эталона, для которого достигается минимум величины ![]() – модуля аргумента
скалярного произведения эталонного поля с объектным:
– модуля аргумента
скалярного произведения эталонного поля с объектным: ![]() . По своему физическому
смыслу
. По своему физическому
смыслу ![]() есть истинное значение интегральной
разности фаз в отсутствие шумов. По аналогии можно ввести коэффициент
амплитудного расхождения, учитывающий несоответствие амплитудных радиоголограмм
исследуемого объекта и эталона, выбранного для сравнения –
есть истинное значение интегральной
разности фаз в отсутствие шумов. По аналогии можно ввести коэффициент
амплитудного расхождения, учитывающий несоответствие амплитудных радиоголограмм
исследуемого объекта и эталона, выбранного для сравнения – ![]() .
.
В дальнейшем будем
рассматривать случай, когда для рассматриваемого диапазона изменения параметров
![]() и
и ![]() возможен
взаимно однозначный переход, как от
возможен
взаимно однозначный переход, как от ![]() и
и ![]() к
к ![]() и
и ![]() , так и обратно. При этом можно рассматривать
задачу построения классификационной сетки не по
, так и обратно. При этом можно рассматривать
задачу построения классификационной сетки не по ![]() , а по
, а по
![]() и
и ![]() . Для
сокращения записи будем опускать аргумент у величин
. Для
сокращения записи будем опускать аргумент у величин ![]() и
и
![]() .
.
Построение классификационной сетки
эталонов на основе ![]() и
и ![]()
В работе [4] авторами
было получено выражение для функции плотности вероятности оцениваемой в МФМ
величины ![]() . Используя их в соответствии с
методикой, описанной в [5], можно получить оценки вероятностей
. Используя их в соответствии с
методикой, описанной в [5], можно получить оценки вероятностей ![]() и
и ![]() в
форме простой границы Чернова [5–6]:
в
форме простой границы Чернова [5–6]:
![]() (1)
(1)
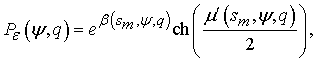 (2)
(2)
где
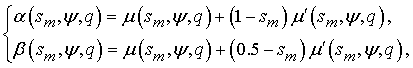 (3)
(3)
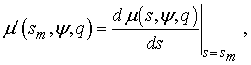 (4)
(4)
В выражении (4) ![]() – производящая функция моментов
функционала отношения правдоподобия:
– производящая функция моментов
функционала отношения правдоподобия:
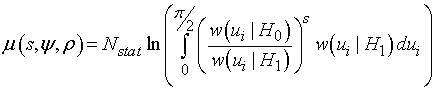 , (5)
, (5)
для случая задачи проверки простой гипотезы H0 против сложной альтернативы H1:
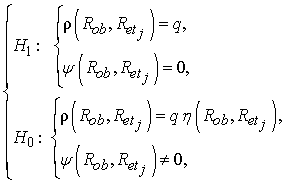 (6)
(6)
выраженная через плотность распределения вероятности интегральной разности фаз:
где
![]() ,
, ![]() –
функция ошибок,
–
функция ошибок, ![]() – коэффициент, равный
произведению отношения сигнал/шум (ОСШ) q
и коэффициента амплитудного расхождения
– коэффициент, равный
произведению отношения сигнал/шум (ОСШ) q
и коэффициента амплитудного расхождения ![]() ,
который в дальнейшем, если не оговорено противное, будем полагать известным и
равным.
,
который в дальнейшем, если не оговорено противное, будем полагать известным и
равным.
Точка ![]() выбирается из условия минимизации логарифма
производящей функции моментов
выбирается из условия минимизации логарифма
производящей функции моментов ![]() и определяет величину
порога, с которым сравнивается функционал отношения правдоподобия. В
предположении равноправия ошибок первого и второго рода для рассматриваемой
задачи проверки статистической гипотезы (случай, который и будет рассмотрен в
дальнейшем), порог будет равен 1, что соответствует
и определяет величину
порога, с которым сравнивается функционал отношения правдоподобия. В
предположении равноправия ошибок первого и второго рода для рассматриваемой
задачи проверки статистической гипотезы (случай, который и будет рассмотрен в
дальнейшем), порог будет равен 1, что соответствует ![]() .
.
Под минимальным шагом
сетки эталонов будем подразумевать величину ![]() ,
при которой для заданного объёма выборки и отношения сигнал/шум достигается
необходимое значение
,
при которой для заданного объёма выборки и отношения сигнал/шум достигается
необходимое значение ![]() или
или ![]() .
.
На рисунках
1 – 4 изображены зависимости ![]() и
и ![]() от значения q при различных объёмах выборки,
доступной для анализа, и различных значений шага сетки
от значения q при различных объёмах выборки,
доступной для анализа, и различных значений шага сетки ![]() .
.
Стоит отметить, что такая
система классификации значительно более чувствительна к увеличению ![]() , чем Nstat. Например, разряжение сетки в 2 раза
(с 1° до 2°) приводит к выигрышу во входном ОСШ около 3 дБ (см. рис. 1).
Для достижения такого же эффекта необходимо (при фиксированном
, чем Nstat. Например, разряжение сетки в 2 раза
(с 1° до 2°) приводит к выигрышу во входном ОСШ около 3 дБ (см. рис. 1).
Для достижения такого же эффекта необходимо (при фиксированном ![]() ) увеличить Nstat в 12,5 раз (с 200 до 2500) (см. рис. 2).
) увеличить Nstat в 12,5 раз (с 200 до 2500) (см. рис. 2).
Из анализа характеристик
можно сделать заключение о том, что ![]() (
(![]() ) возрастает (уменьшается) с увеличением
как
) возрастает (уменьшается) с увеличением
как ![]() , так и
, так и ![]() .
Однако очевидно, что данные зависимости носят нелинейный характер и, например,
для достижения заданного уровня
.
Однако очевидно, что данные зависимости носят нелинейный характер и, например,
для достижения заданного уровня ![]() постоянное увеличение
объёма выборки на фиксированную величину приводит к уменьшению энергетического
выигрыша во входном ОСШ, при котором данная
постоянное увеличение
объёма выборки на фиксированную величину приводит к уменьшению энергетического
выигрыша во входном ОСШ, при котором данная ![]() достигается.
Тот же вывод можно сделать и по поводу уменьшения полной ошибки.
достигается.
Тот же вывод можно сделать и по поводу уменьшения полной ошибки.
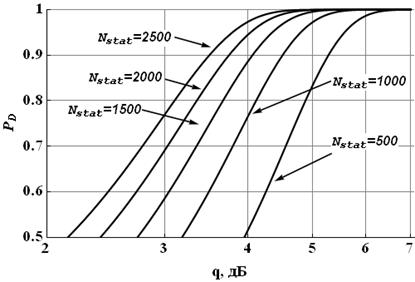
Рис. 1. Зависимость PD от отношения сигнал/шум при ψ = 5° и различных Nstat
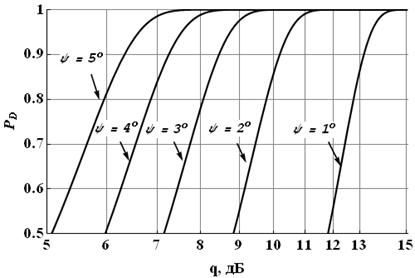
Рис. 2. Зависимость PD от отношения сигнал/шум при Nstat = 2500 и различных ψ
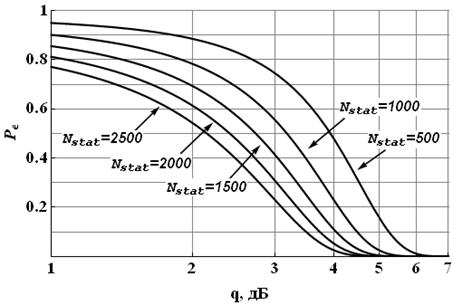
Рис. 3. Зависимость Pε от отношения сигнал/шум при ![]() = 5° и различных Nstat
= 5° и различных Nstat
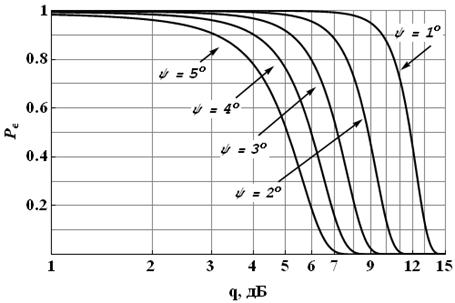
Рис.4. Зависимость Pε от отношения сигнал/шум при Nstat = 2500 и различных ![]()
Исходя из этих
зависимостей, можно сделать заключение о необходимости крайне аккуратного
синтеза системы классификации с учётом особенностей конкретных объектов,
рассматриваемых на практике. Так, попытка резкого увеличения количества
используемых эталонов – уменьшение шага по ![]() (для
повышения разрешающей способности метода), может привести к необходимости
серьёзного повышения объема выборки
(для
повышения разрешающей способности метода), может привести к необходимости
серьёзного повышения объема выборки ![]() и, как следствие, к
снижению быстродействия системы в целом (одного главных её преимуществ) или,
при сохранении фиксированного
и, как следствие, к
снижению быстродействия системы в целом (одного главных её преимуществ) или,
при сохранении фиксированного ![]() , к снижению
, к снижению ![]() за счёт того, что система будет чаще
«путать» мало различающиеся по оцениваемому параметру эталоны.
за счёт того, что система будет чаще
«путать» мало различающиеся по оцениваемому параметру эталоны.
Полученные зависимости
могут быть использованы для формирования рекомендаций при проектировании систем
голографического радиовидения. В частности, фиксирование требуемого значения ![]() или
или ![]() при
наличии существующей схемотехнической реализации (аппаратно заданном объёме
статистической выборки) позволяет определить минимальный шаг сетки эталонов (и,
как следствие, оценить сверху максимально возможную точность), а так же
управлять им за счёт изменения отношения сигнал/шум, например, используя
дополнительную предобработку регистрируемого сигнала. При невозможности
улучшения отношения сигнал/шум полученные зависимости позволяют указать способ
повышения точности оценки (уменьшения минимального шага) увеличивая на заданную
величину объём выборки, т.е. задают требования для модификации аппаратной части
(так как нередко увеличение объёма выборки при сохранении желаемого времени
оценки невозможно без изменения аппаратной реализации узлов СРГВ).
при
наличии существующей схемотехнической реализации (аппаратно заданном объёме
статистической выборки) позволяет определить минимальный шаг сетки эталонов (и,
как следствие, оценить сверху максимально возможную точность), а так же
управлять им за счёт изменения отношения сигнал/шум, например, используя
дополнительную предобработку регистрируемого сигнала. При невозможности
улучшения отношения сигнал/шум полученные зависимости позволяют указать способ
повышения точности оценки (уменьшения минимального шага) увеличивая на заданную
величину объём выборки, т.е. задают требования для модификации аппаратной части
(так как нередко увеличение объёма выборки при сохранении желаемого времени
оценки невозможно без изменения аппаратной реализации узлов СРГВ).
В случае построения
достаточно разреженной сетки эталонов и большого количества усреднений можно
достичь достаточно малых значений необходимого входного ОСШ, например, при ![]() = 10° и Nstat = 2500 значение
= 10° и Nstat = 2500 значение ![]() = 0,999 достигается при q = 5 дБ, а значение
= 0,999 достигается при q = 5 дБ, а значение ![]() = 10-10
достигается при q = 6 дБ, что с практической точки зрения является
невысокими и реализуемыми требованиями.
= 10-10
достигается при q = 6 дБ, что с практической точки зрения является
невысокими и реализуемыми требованиями.
Построение классификационной сетки эталонов с использованием СПР
Как указывается в [4] и
[7], плотность вероятности (ПВ) величины ![]() является
функцией входного ОСШ q,
истинного значения параметра
является
функцией входного ОСШ q,
истинного значения параметра ![]() (значение модуля
аргумента скалярного произведения в отсутствии шумов при сравнении с некоторым
фиксированным эталоном) и коэффициента амплитудного расхождения
(значение модуля
аргумента скалярного произведения в отсутствии шумов при сравнении с некоторым
фиксированным эталоном) и коэффициента амплитудного расхождения ![]() между исследуемым объектом и выбранным
для сравнения эталоном.
между исследуемым объектом и выбранным
для сравнения эталоном.
Используя методику,
описанную в [3], определим минимальный шаг сетки эталонов как значение
статистического предела разрешения при оценке величины ![]() на основе Nstat измерений. Тогда в соответствии с
[3], [9-11]:
на основе Nstat измерений. Тогда в соответствии с
[3], [9-11]:
![]() ,
(8)
,
(8)
где ![]() -
нижняя граница Рао-Крамера для дисперсии любой несмещённой оценки
-
нижняя граница Рао-Крамера для дисперсии любой несмещённой оценки ![]() параметра
параметра ![]() . В
соответствии с [8] граница Рао-Крамера для случая оценки скалярного параметра
. В
соответствии с [8] граница Рао-Крамера для случая оценки скалярного параметра ![]() имеет вид:
имеет вид:
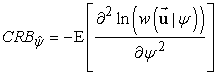 , (9)
, (9)
где ![]() означает
операцию усреднения по выборке в точке истинного значения параметра, а
означает
операцию усреднения по выборке в точке истинного значения параметра, а ![]() – вектор выборки.
– вектор выборки.
Для случая функции плотности вероятности (7) выражение для границы Рао-Крамера примет вид:
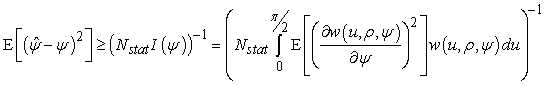 ,
(10)
,
(10)
где 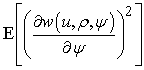 определяется
выражением:
определяется
выражением:
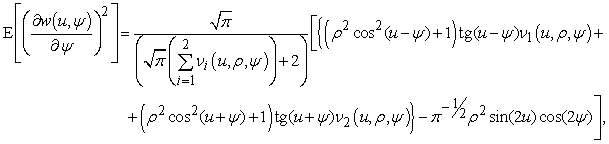 (11)
(11)
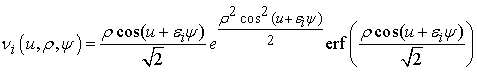 ,
(12)
,
(12)
а ![]() ,
, ![]() .
.
В случае же оценки
некоторого векторного параметра ![]() :
:
![]() ,
(13)
,
(13)
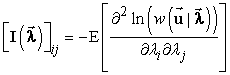 .
(14)
.
(14)
В нашем случае ![]() . Заметим, что при оценке величины
. Заметим, что при оценке величины ![]() на основе Nstat измерений неизвестное значение
на основе Nstat измерений неизвестное значение ![]() является мешающим параметром.
является мешающим параметром.
На рисунках
5 – 8 изображены зависимости СПР от значения q при различных объёмах выборки,
доступной для анализа, и различных значений шага сетки ![]() для случая как известного, так и
неизвестного
для случая как известного, так и
неизвестного ![]() .
.
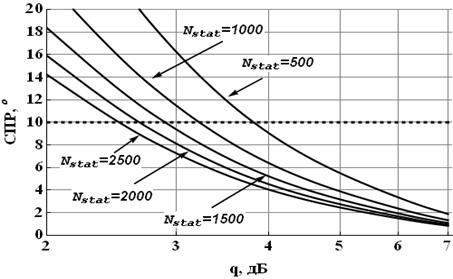
Рис.5. Зависимость СПР от отношения
сигнал/шум при различном Nstat (![]() =10°,
=10°, ![]() =1)
для случая неизвестного
=1)
для случая неизвестного ![]()
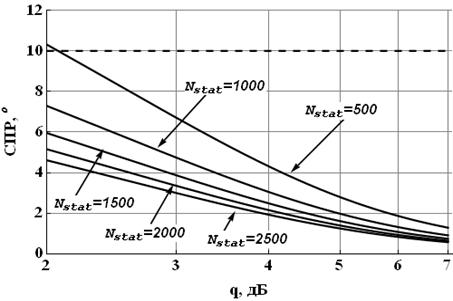
Рис. 6. Зависимость СПР от отношения
сигнал/шум при различном Nstat (![]() =10°,
=10°, ![]() =1)
для случая известного
=1)
для случая известного ![]()
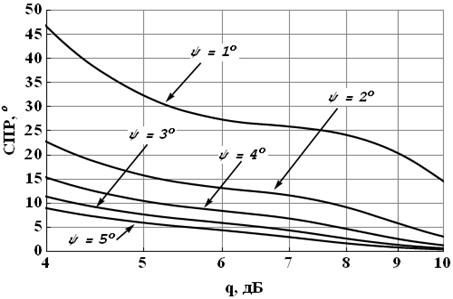
Рис. 7. Зависимость СПР от отношения
сигнал/шум при различном ![]() (Nstat=2500,
(Nstat=2500, ![]() =1) для
случая неизвестного
=1) для
случая неизвестного
![]()
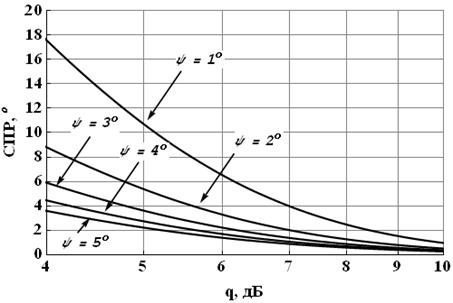
Рис. 8 Зависимость СПР от отношения
сигнал/шум при различном ![]() (Nstat=2500,
(Nstat=2500, ![]() =1) для
случая известного
=1) для
случая известного ![]()
Важно отметить, что величина статистического предела разрешения существенно зависит от знания амплитудного расхождения, что, соответственно, накладывает дополнительное требование проведения его предварительной оценки.
Исходя из этих
зависимостей, можно сделать заключение о том, что попытка резкого увеличения
количества используемых эталонов – уменьшение шага по ![]() (для повышения разрешающей
способности метода) может привести к необходимости серьёзного повышения объема
выборки Nstat и, как следствие, к снижению
быстродействия системы в целом (одного главных её преимуществ).
(для повышения разрешающей
способности метода) может привести к необходимости серьёзного повышения объема
выборки Nstat и, как следствие, к снижению
быстродействия системы в целом (одного главных её преимуществ).
По результатам
проведённого исследования было отмечено уменьшение степени влияния объёма
выборки на выигрыш в соотношении сигнал/шум при определении минимального шага
сетки эталонов с использованием статистического критерия разрешения в случае
наличия априорной неопределённости относительно величины коэффициента амплитудного
расхождения. При этом априорное знание величины коэффициента амплитудного расхождения
снижает требования на необходимое отношение сигнал/шум (для обеспечения требуемого
минимального шага сетки) на величину порядка 2,5 - 4 дБ при ![]() от 1° до 10° и объёме
выборки от 100 до 2500 отсчётов. При этом степень влияния объёма выборки при
его увеличении снижается.
от 1° до 10° и объёме
выборки от 100 до 2500 отсчётов. При этом степень влияния объёма выборки при
его увеличении снижается.
Заключение
Таким образом, решена задача анализа границ качества минимально-фазового метода эталонной оценки параметров объектов по радиоголограмме.
Полученные характеристики могут использоваться для определения необходимого объёма выборки при фиксированной эталонной сетке или для формирования эталонной сетки при заданном объёме выборки для обеспечения требуемой вероятности правильной/ошибочной классификации.
На основе полученных характеристик можно выдать рекомендации к процессу проектирования систем, использующих МФМ:
- при q менее 5 дБ и Nstat менее 2500 отсчётов минимальный шаг эталонной сетки не должен быть более 5° (независимо от наличия априорной информации об η);
-
при использовании
разреженной сетки с ![]() ≥10° возможно добиться
низких требований на
≥10° возможно добиться
низких требований на ![]() (около 2 дБ) даже при
использовании Nstat менее 1000.
(около 2 дБ) даже при
использовании Nstat менее 1000.
Стоит так же отметить,
что два предлагаемых подхода могут давать различающиеся значения минимального
шага сетки. В этом случае разумно в качестве шага брать максимальное значение
из двух, что заведомо обеспечит требуемую разрешающую способность при заданной ![]() или
или ![]() .
.
1. Bennett C., Toomey J. Target classification with multiple frequency illumination // IEEE Transactions on Antennas and Propagation. – 1981. – Vol. 29, № 2. – P. 352—358.
2. Gvozdaryev A. S., Artyomova T. K. Minimum-phase method for the reference estimation of object size in problems of RF holography // Radioelectronics and Communications Systems. – 2011. – Vol. 54. – P. 189-195.
3. Smith S. T. Statistical resolution limits and the complexified Cramer-Rao bound // IEEE Transactions on Signal Processing. – 2005. – Vol. 53, № 5. – P. 1597—1609.
4. Гвоздарёв А.С., Артёмова Т.К. Способ повышения качества эталонной оценки размеров объектов радиоголографии в условиях малоэлементной антенной решётки // Известия высших учебных заведений России. Радиоэлектроника. – 2012. – № 1. – С. 65–74.
5. Ван Трис Г. Теория обнаружения, оценок и модуляции (в 4 томах) / Г. Ван Трис. – М.: Сов. Радио, 1972. – Т. I: Теория обнаружения, оценок и линейной модуляции / ред., пер. В. И. Тихонов, 1972.
6. Gallager R. G. Lower Bounds on the Tails of Probability Distributions // M.I.T., RLE/QPR. – 1965. – № 77. – P. 277-291.
7. Гвоздарёв А.С., Артёмов К.С., Артёмова Т.К. Анализ границ качества минимально-фазового метода эталонной оценки параметров объектов по радиоголограмме // Труды XVIII международной научно-технической конференции «Радиолокация, навигация, связь. – Воронеж. – T.1. – С. 168 – 178.
8. Kay S. M. Fundamentals of Statistical Signal Processing. – NY: Prentice Hall, 1993. – Vol.1.
9. Amar A., Weiss A. Fundamental limitations on the resolution of deterministic signals // IEEE Transactions on Signal Processing. – 2005. – Vol. , № 11. – P. 5309–5318.
10. Delmas J.-P., Р. Abeida Statistical resolution limits of DOA for discrete // Proceedings of IEEE International Conference on Acoustic, Speech, Signal Processing (Toulouse, France, 2006). – Vol. 4. – P. 889—892.
11. El Korso M. N., Boyer R., Renaux A., Marcos S. Statistical resolution limit: Application to passive polarized source localization // 5ie´me seminaire sur les systemes de detection: architecture et technologies. (Alger, 21–23 fevrier 2011).