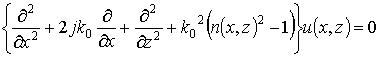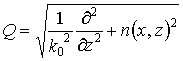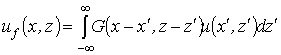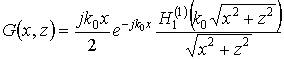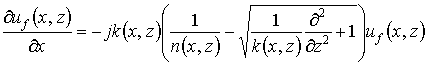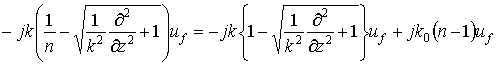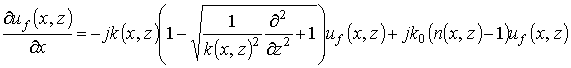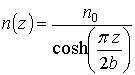УДК 621.396.961

ИССЛЕДОВАНИЕ ЛИНЗОВЫХ АНТЕНН ИЗ НЕОДНОРОДНОГО ДИЭЛЕКТРИКА МЕТОДОМ ПАРАБОЛИЧЕСКОГО УРАВНЕНИЯ

 

В. В. Ахияров

МГТУ им. Н.Э. Баумана

Статья поступила в редакцию 27 ноября 2015 г.

 

Аннотация. В работе представлено новое параболическое уравнение для волн в среде из неоднородного диэлектрика, и рассмотрен алгоритм его решения. Выполнена проверка полученного алгоритма на примере исследования фокусирующих свойств цилиндрических линз Микаэляна и Максвелла. Представлены результаты расчетов поля в ближней и дальней зоне для антенны на основе градиентной и радиально-слоистой линзы Максвелла. Рассмотрено возбуждение планарной радиально-слоистой линзы Люнебурга волной H₁₀ и выполнено сравнение расчетов методом ПУ с результатами строгого электродинамического моделирования. Результаты работы были доложены на III Всероссийской Микроволновой конференции.

Ключевые слова: линзовые антенны, параболическое уравнение, диаграмма направленности.

Abstract. In this article a new parabolic equation for wave propagation inside inhomogeneous dielectric media is presented and an algorithm of its solution is treated. That algorithm is verified using the Mikaelian and Maxwell cylindrical lenses focusing properties. The near-field and far-field calculations for the gradient and radial-layered Maxwell lens antenna are done. The design of planar radially-layered Luneberg lens with H₁₀ wave excitation is considered and comparison parabolic equation technique with a rigorous solution is produced. The presented results were reported at the III Microwave week.

Keywords: lens antennas, parabolic equation, radiation pattern.

 

Как правило, задача анализа линзовых антенн из неоднородного диэлектрика решается в приближении геометрической оптики, либо численными методами с использованием программ САПР СВЧ-устройств; при наличии цилиндрической, либо сферической симметрии возможно использование метода разделения переменных.

В [1] было показано, что метод параболического уравнения (ПУ) обеспечивает высокую точность решения скалярных задач излучения и дифракции на телах большого электрического размера, при этом показатель преломления среды распространения радиоволн полагается равным единице. В данной работе представлено обобщение рассмотренного в [1] ПУ на случай произвольного изменения показателя преломления в области, ограниченной поверхностью линзы. Строгое решение данной задачи должно удовлетворять уравнению Гельмгольца для амплитуды поля  [2]:

,           (1)

где  – волновое число в свободном пространстве, x и z – продольная (в направлении распространения радиоволн) и поперечная координаты,  определяется законом изменения показателя преломления в линзе.

С использованием метода факторизации (1) приводится к двум параболическим уравнениям для волн, распространяющихся в противоположных направлениях. Если при возбуждении линзы из неоднородного диэлектрика не учитывать обратное рассеяние, рассматриваемая задача сводится к решению ПУ для волн, уходящих от источника:

,                                       (2)

где

.                                                 (3)

         При  известно аналитическое решение ПУ (2) в виде интеграла свертки [3]:

,                             (4)

с ядром

,                            (5)

где  – функция Ханкеля первого рода первого порядка.

         В задаче анализа линзовых антенн требуется найти решение ПУ (2) с некоторой функциональной зависимостью  внутри линзы. Для этого в работе [4] использовалось приближенное представление дифференциального оператора:

,                                                        (6)

где 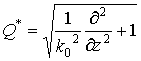 – оператор для свободного пространства.

После подстановки (6) в (2) получим уравнение

,      (7)

 

решение которого основано на вычислении интеграла свертки (4).

Как показали результаты расчетов, приближение (6) дает существенную погрешность при вычислении диаграммы направленности линзовой антенны по сравнению со строгими методами электродинамического моделирования. Поэтому требуется найти решение параболического уравнения (2) с исходным оператором (3). Для этого представим (3) в виде:

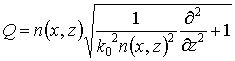                                        (8)

и после подстановки (8) в (2) получим:

,                                (9)

где .

         Далее выполним преобразование правой части уравнения (9):

,                  (10)

где для компактности записи аргументы у функций опускаются.

Подстановка (10) в (9) дает искомое параболическое уравнение:

,    (11)

при этом, как и в уравнении (7),  функция  вынесена из-под радикала, что позволяет использовать известное решение (4) для ПУ с оператором

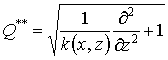.                                                                                    (12)

Выражение (12) отличается от оператора для свободного пространства  заменой волнового числа k₀ на функцию , которая учитывает распределение показателя преломления в материале линзы. Отметим, что такая замена не влияет на алгоритм численного решения ПУ (11).

         При  последнее слагаемое в (11) равно нулю и в этом случае из уравнения (11) следует хорошо известное ПУ для свободного пространства, использованное в [1] для решения задач излучения и дифракции.

Следует отметить, что ПУ (11) отличается от аналогичных уравнений, которые неоднократно рассматривалось в научной литературе [5]. Его основное отличие заключается в том, что оно является строгим для волн, уходящих от источника, поскольку при его выводе не было сделано никаких допущений.

            Для решения ПУ (11) используется стандартный алгоритм, основанный на вычислении интеграла свертки (4) с использованием быстрого преобразования Фурье по координате z:

,                                    (13)

 

где в ядре свертки  волновое число k₀ следует заменить на .

Начальное распределение поля , необходимое для численных расчетов, определяется полем источника и поэтому считается известным. Диаграмма направленности (ДН) антенны определяется интегрированием полученного распределения ближнего поля по поперечной координате, аналогично тому, как это было сделано при вычислении ДН параболической антенны в работе [1].

Использование ПУ (11) позволяет решить задачу фокусировки поля источника (нити тока) цилиндрическими линзами из неоднородного диэлектрика. В качестве объектов для исследования были выбраны линзы Микаэляна и Максвелла, поскольку положения их геометрооптических фокусов хорошо известны.

Показатель преломления линзы Микаэляна зависит только от одной декартовой координаты [6]:

,                                                                                         (14)

где 2b – ширина линзы.

Толщина линзы 2z_max выбирается из условия . Результаты расчетов по формуле (14) при  представлены на рис.1. На рис.2.а и 2.б показано распределение амплитуды поля  и ее действительной части , полученные в результате решения ПУ (11) с использованием алгоритма (13). Ширина линзы выбрана равной , ее толщина , нить тока расположена на поверхности линзы в точке с координатами (0,0). Как видно из рис.2.а, максимум амплитуды поля наблюдается в фокусе на противоположной поверхности линзы; представление о поведении волнового фронта внутри линзы дает рис.2.б.

Представленная на рис.3 зависимость  позволяет уточнить положение фокуса линзы Микаэляна. Результаты расчетов свидетельствуют о том, что фокус смещен на расстояние  наружу линзы, что соответствует отклонению от геометрооптического фокуса на 1%.

 

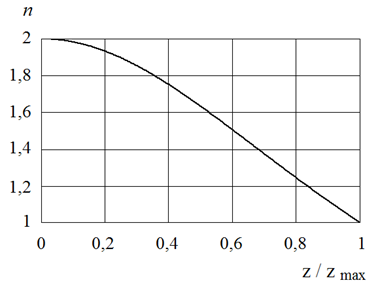
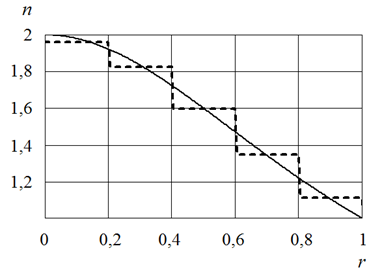
Рис.1. Закон изменения показателя преломления в линзе Микаэляна

 

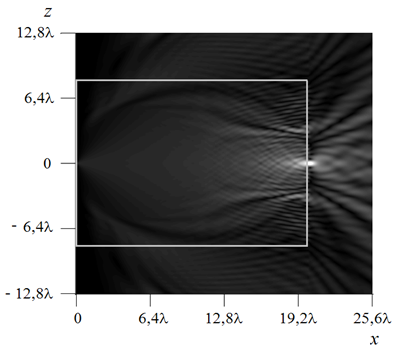
а)

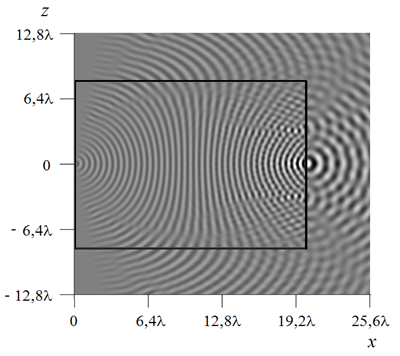
б)

Рис.2. Амплитуда поля (а) и ее действительная часть (б) в линзе Микаэляна

 

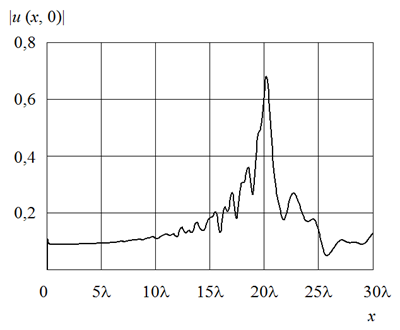
Рис.3. Распределение амплитуды поля вдоль оси линзы Микаэляна

 

Далее исследуем линзу Максвелла, которая обладает центральной симметрией, радиальная зависимость показателя преломления в линзе определяется выражением [6]:

.                                                     (15)

 

На практике используется дискретное изменение , что соответствует линзе из концентрических слоев диэлектрика с постоянным показателем преломления в пределах каждого слоя. На рис.4 показаны результаты расчетов показателя преломления по формуле (15) и аппроксимация  пятью цилиндрическими слоями равной ширины.

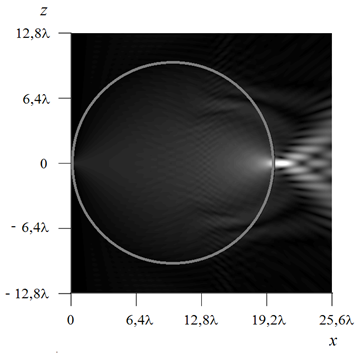
На рис.5.а и 5.б приведены результаты расчетов  и ,  полученные при возбуждении градиентной линзы Максвелла диаметром  нитью тока, расположенной в точке с координатами (0, 0) на поверхности линзы.

 

Рис.4. Закон изменения показателя преломления в градиентной

(сплошная линия) и слоистой (штриховая линия) линзе Максвелла

 

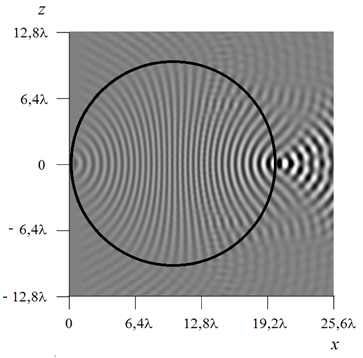
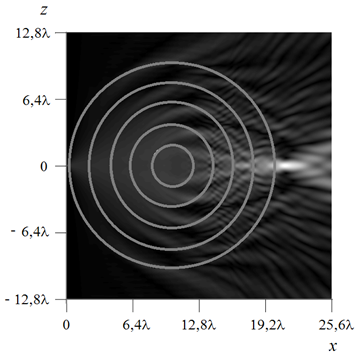
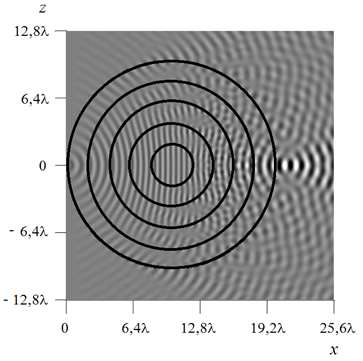
Хорошо видно, что линза фокусирует поле источника в диаметрально противоположную точку (рис.5.а), трансформацию волнового фронта в линзе можно наблюдать на рис.5.б. Результаты решения аналогичной задачи для линзы того же диаметра из пяти цилиндрических слоев равной ширины показаны на рис.6.а и 6.б. Полученное распределение амплитуды поля свидетельствуют о том, что линза сохраняет свои фокусирующие свойства (рис.6.а), однако волновые фронты внутри линзы терпят разрывы вследствие резких скачков показателя преломления на границе слоев (рис.6.б). Представленные на рис.7 распределения амплитуды поля вдоль диаметра позволяют уточнить положения фокусов градиентной и слоистой линзы. Полученные распределения свидетельствуют о том, что в обоих случаях фокус находится снаружи от поверхности линзы, причем для слоистой линзы он смещен более существенно. Максимум амплитуды поля для градиентной линзы находится на расстоянии  от ее поверхности, что соответствует отклонению от геометрооптического фокуса на 3,75%, для слоистой линзы отклонение составляет 5,5%. Также необходимо отметить меньшую амплитуду поля в фокусе слоистой линзы.

Существенно худшие фокусирующие свойства слоистой линзы Максвелла вызваны тем, что при диаметре линзы  в линзе из пяти слоев толщина слоя равна двум длинам волн.

 

а)

б)

Рис.5. Амплитуда поля (а) и ее действительная часть (б)

в градиентной линзе Максвелла

 

а)

б)

Рис.6. Амплитуда поля (а) и ее действительная часть (б)

в линзе Максвелла из пяти слоев

 

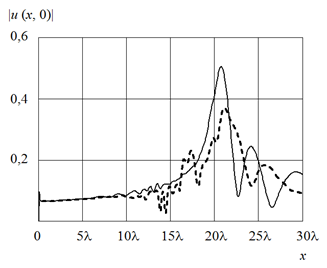
Рис.7. Распределение амплитуды поля по диаметру линзы Максвелла.

Сплошная линия – градиентная линза, пунктир – линза из пяти слоев

 

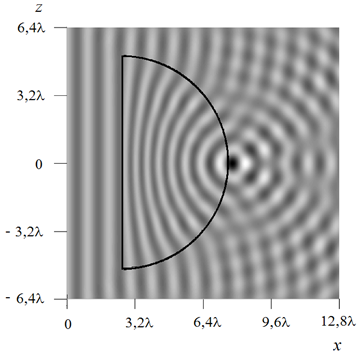
Для того, чтобы линзу Максвелла можно было рассматривать как антенну, волновой фронт на ее выходе должен быть плоским; этого можно достичь при использовании половины линзы. На рис.8.а, б представлено распределение  для линзы диаметром  с непрерывным и дискретным законом изменения  при ее облучении плоской волной.

 

а)

б)

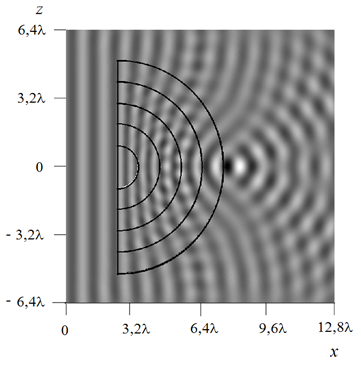
Рис.8. Действительная часть амплитуды поля в антенне на основе

градиентной (а) и слоистой (б) линзы Максвелла

 

Видно, что падающая волна фокусируется вблизи левой границы линзы (точка с координатами ), положение фокуса уточняется с использованием распределения амплитуды поля по диаметру линзы (см. рис.9). Как и в предыдущем случае, фокус линзы смещен в наружную область на расстояние  для градиентной линзы и  для слоистой, что соответствует отклонению от геометрооптического фокуса на 3,5% и 6,5%.

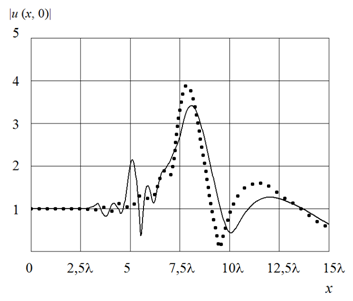
Рис.9. Распределение амплитуды поля при облучении антенны

на основе линзы Максвелла плоской волной.

Сплошная линия – линза из пяти слоев, пунктир – градиентная линза

 

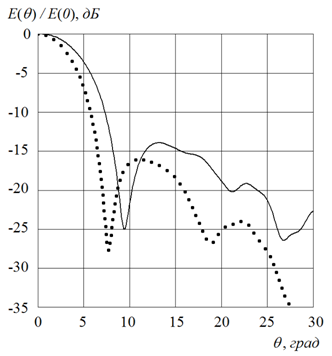
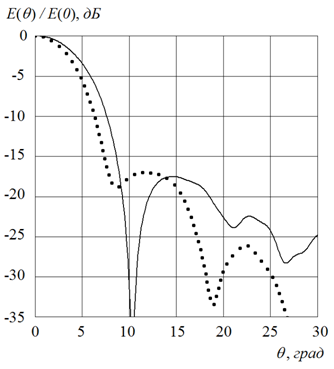
На рис.10.а приведены диаграммы направленности градиентной и радиально-слоистой линзы Максвелла при ее возбуждении нитью тока, радиально-слоистая линза была синтезирована из пяти слоев равной ширины (см. рис.4), источник размещался в фокусе линзы. Ширина луча ДН градиентной линзы – 6,9⁰, для слоистой линзы получено значение 9,2⁰. На рис.10.б показаны результаты аналогичных расчетов при возбуждении линзы плоской апертурой шириной , размещенной в ее фокусе. При этом ширина ДН градиентной линзы равна 7,7⁰, слоистой – 9,4⁰, уровень боковых лепестков (УБЛ) становится меньше по сравнению со случаем возбуждения линзы нитью тока.

 

а)

б)

Рис.10. Диаграмма направленности линзы Максвелла при возбуждении

нитью тока (а) и апертурой шириной  (б).

Пунктир – градиентная линза. Сплошная линия – линза из пяти слоев

 

Полученные результаты решения скалярных задач фокусировки и излучения поля линзами из неоднородного диэлектрика позволяют рассмотреть практическую конструкцию планарной антенны на основе линзы Люнебурга с цилиндрической симметрией. Сверху и снизу линза ограничена металлическими дисками, диаметр дисков равен диаметру линзы, для ее возбуждения используется отрезок прямоугольного волновода (см. рис.11). В отличие от рассмотренного в [4] случая возбуждения подобной линзы TEM волной, в данной работе задача решается для волны Н₁₀, при этом закон изменения показателя преломления от радиуса линзы имеет вид:

,                                         (16)

где а и g – радиус и толщина линзы.

 

Рис.11. Планарная линза Люнеберга

 

Все дальнейшие расчеты выполнялись для линзы из пяти концентрических слоев равной ширины диаметром 100 мм и толщиной 7,2 мм, длина волны – λ = 8,6 мм. Результаты расчета показателя преломления в градиентной и слоистой линзе для выбранных исходных данных представлены на рис.12.

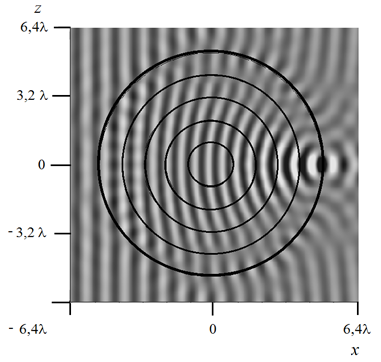
На рис.13 показана действительная часть амплитуды поля, полученная при облучении линзы Люнебурга плоской волной с вектором Е, параллельным металлическим дискам. Видно, что волновой фронт сходится к фокусу линзы, при этом решение ПУ (рис.13.а) соответствует аналогичным расчетам для планарной линзы, которые были получены с использованием строго метода моментов (рис.13.б). Представленное на рис.14 распределение амплитуды поля позволяет уточнить положение фокуса: метод ПУ (сплошная линия) дает максимальное значение амплитуды поля на расстоянии x = 48 мм, по методу моментов (штриховая линия) фокус получен практически на границе линзы при x = 49,5 мм (x = 0 мм соответствует центру линзы). Таким образом, погрешность в определении положения фокуса методом ПУ для линзы диаметром 100 мм составляет 1,5%.

 

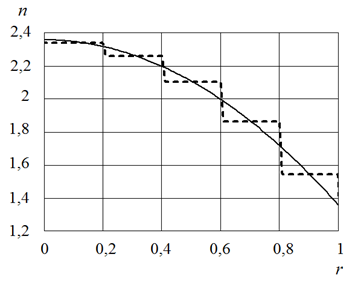
Рис.12. Закон изменения показателя преломления в слоистой линзе Люнебурга

 

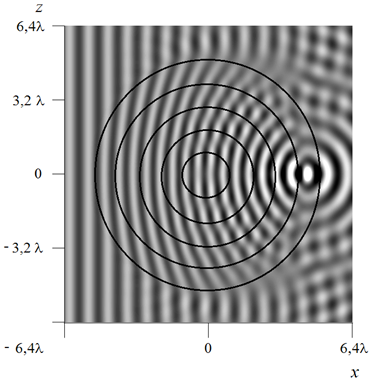
а)

 

б)

Рис.13. Действительная часть амплитуды поля при облучении линзы

Люнебурга плоской волной. а) метод ПУ, б) метод моментов

 

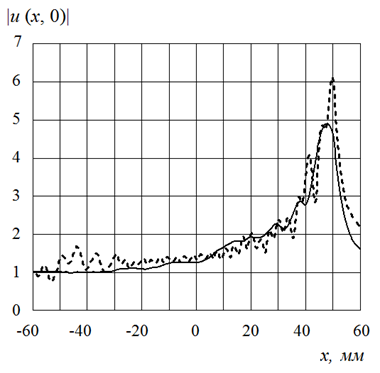
Рис.14. Положение фокуса линзы

 

На рис.15 представлены результаты расчетов ДН слоистой линзы Люнебурга методом ПУ (сплошная линия) и методом моментов (пунктир). В обоих случаях источник, в качестве которого был выбран отрезок прямоугольного волновода сечением 6,0 x 7,2 мм, размещался в фокусе линзы, положение которого определялось в соответствии с рис.14. Видно, что форма ДН, полученная методом ПУ при решении скалярной задачи, практически полностью соответствует аналогичной зависимости для планарной линзы. На рис.16 представлены результаты расчетов методом ПУ для градиентной линзы, показатель преломления которой определяется формулой (16), а также для линзы из трех и пяти слоев равной ширины. Видно, что во всех трех случаях форма главного лепестка ДН остается практически неизменной, однако уровень боковых лепестков слоистой линзы увеличивается, при этом для линзы из трех слоев УБЛ не превышает -14 дБ.

 

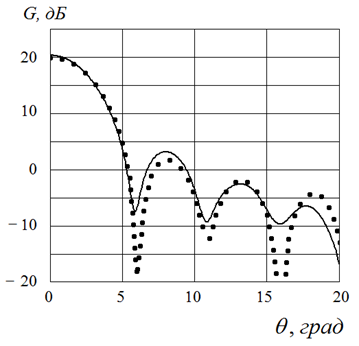
Рис.15. ДН линзы из пяти слоев. Сплошная линия – метод ПУ,

пунктир – метод моментов

 

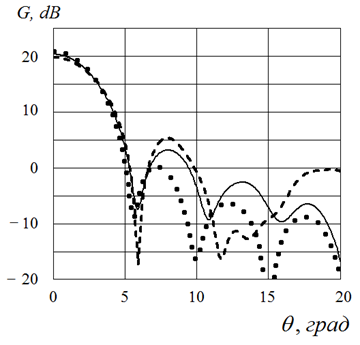
Рис.16. ДН  линзовых антенн. Пунктир – градиентная линза,

сплошная кривая – пять слоев, штриховая кривая – три слоя диэлектрика

 

На основании представленных результатов можно сделать вывод о том, что полученное в данной работе ПУ позволяет с высокой точностью определять положение фокуса в линзах из неоднородного диэлектрика. Результаты расчетов диаграммы направленности планарной антенны на основе цилиндрической линзы Люнебурга показали очень хорошее соответствие метода ПУ и строгого метода моментов в пределах ±15⁰ относительно направления максимума излучения.

Автор выражает признательность В.А. Калошину за постановку задачи и полезные обсуждения.

 

Литература

1.     Ахияров В.В. Результаты решения скалярных задач излучения и дифракции методом параболического уравнения // Электромагнитные волны и электронные системы. 2014. №2. C.12-18.

2.     Ахияров В.В. Метод параболического уравнения в теории дифракции // Успехи современной радиоэлектроники. 2010. №9. C. 72-80.

3.     Ахияров В.В. Решение задач дифракции методом параболического уравнения // Электромагнитные волны и электронные системы. 2012. №11. C.24-30.

4.     Ахияров.В.В., Калошин В.А., Никитин Е. Исследование широкополосных планарных линз Люнебурга // Журнал радиоэлектроники. 2014. №1.

5.     Levy М.F. Parabolic equation method for electromagnetic wave propagation. London. IEE. 2000. 336 p.

6.     Зелкин Е.Т., Петрова Р.А. Линзовые антенны. М. Сов. Радио. 1974. 280 с.