|
|
"ÆÓÐÍÀË ÐÀÄÈÎÝËÅÊÒÐÎÍÈÊÈ" N 2, 2003 |
|
ATTENUATION OF ELECTROMAGNETIC WAVES BY VEGETATION CANOPIES IN THE 100 – 10000 MHz FREQUENCY BAND
Alexander A. Chukhlantsev, Anatolij M. Shutko, and Sergei P. Golovachev
Institute of Radioengineering and Electronics, Russian Academy of Sciences,
Vvedensky sq., 1, Friazino, Moscow Region, 141190, Russia
Received 09.02.2003
Abstract – An analytical overview of research involving EM waves attenuation by vegetation canopies in the frequency range 100…10000 MHz is given. Brief descriptions of objects of investigation and typical biometric features are presented. The models of vegetation as a continuous medium and as a collection of scatterers are considered. Dielectric properties of vegetative material are discussed. The relation between electromagnetic and biometric parameters of vegetation is established. Methods of measurements of attenuation are reviewed. Available experimental data of attenuation are analyzed and the directions of future research needs are presented.
II. THEORETICAL ASPECTS OF EM WAVES PROPAGATION IN VEGETATION CANOPIES.
1.1. Vegetation canopies as the object of research.
1.3. General approach for EM waves propagation in vegetation.
2. The model of vegetation as a continuous medium.
2.1. EM waves propagation in a random continuous medium.
2.2. Effective dielectric constant of vegetation.
3. The model of vegetation as a collection of scatterers (discrete model).
3.1. EM waves propagation in a random discrete medium.
3.2. Attenuation and scattering of EM waves by plant elements.
4. Dielectric properties of vegetation constituents.
III. EXPERIMENTAL STUDIES OF EM WAVES ATTENUATION IN VEGETATION CANOPIES.
1. The methods of measurements.
2. The results of measurements and their comparison with calculating data.
I. INTRODUCTION
The impact of different types of vegetation, from grassy to forested types, is one of the main problems to be discussed when conducting remote sensing of the land surface. There are two types of interest arising in this area of remote sensing. The first one consists in revealing the screening effect of vegetative cover on the remote sensing of a land surface itself and developing technologies by taking this effect into consideration when assessing the land surface condition. The second one consists of developing technologies of remote sensing application for assessing the properties of vegetative cover. In both cases the attenuation of EM waves and its relation to biometrical features of vegetation is of a great importance.
Prevalence of mobile radio systems requires studies of spectral characteristics of electromagnetic wave attenuation by vegetative media in wide frequency range. It is necessary to assess the influence of vegetation on the quality of radio communication, especially for radio communication in forested terrains.
The investigations mentioned above were actively conducted over the last three decades by groups of scientists working in different countries and institutions including the Institute of Radioengineering and Electronics, Soviet/Russian Academy of Sciences. This paper intends to summarize and to analyze the known theoretical and experimental results on the attenuation of EM waves by vegetation canopies in the frequency range 100 – 10000 MHz.
The paper is prepared under the support of ISTC Project # 2059. The authors thank Prof. B.G. Kutuza, Prof. V.F. Krapivin, Drs. A.G. Grankov, A.A. Milshin, L. Nazarov, A.I. Zakharov, E.N. Zotova, G.G. Yazerian, I. Sidorov, V. Pliushchev, Yu.G. Tishchenko, V.P. Savorsky, and I.I. Chusov for their contribution and for useful discussions. The authors also gratefully thank Prof. S. Murai, a collaborator of the Project from Japan, for his permanent interest to this work.
II. THEORETICAL ASPECTS OF EM WAVES PROPAGATION IN VEGETATION CANOPIES.
1. Basic approaches.
1.1. Vegetation canopies as the object of research.
Vegetation canopies are very dynamic and complicated object of investigation. The morphology of plants changes during the vegetation period leading to a change of vegetation canopy characteristic electrodynamic parameters. From the standpoint of remote sensing the following canopy features are most often used for modeling of EM propagation through a vegetation media [1-3]:
a. Type and stage/phase of growth.
b. Shape and size of leaves, stalks, branches, and trunks.
c. Distributions of leaf, stalk, and branch angles.
d. Volumetric moisture content of plant elements mv.
e. Vegetation volume density p (the relative volume occupied by vegetation in canopy); p = nVs, where Vs is the volume of plant element, n is the number density of elements.
f. Vegetation water content per unit volume w = pmvrw, where rw is the density of water.
g. The number of plants (trunks) per unit area N.
h. Vegetation average height h.
i. Vegetation wet biomass Q (the weight of vegetation per unit area).
j. Vegetation water content per unit area W.
k. Vegetation gravimetric moisture m = W/Q.
Some biometric features of agricultural vegetation are collected from different sources and are presented in Table 1. These data can be useful for modeling of attenuation by main crops during the vegetation period. The change of biometric parameters of crops during a growing process can be found in [5-11, 162].
Forests occupy a third of the Earth’s land surface (about 50 millions square kilometers) and play a key role in the formation of global circulation of carbon and nitrogen and in the influence upon the energy and water balance of the biosphere. Boreal forests of Europe, Russia, Canada, and USA occupy about 15 millions square kilometers. Tropical forests make up about 53% of the world forest store.
A characteristic feature of forests is the tier structure. The basic components of forest phytocenosis are stand, undergrowth, live soil cover, and dead litter [12, 13].
The stand consists of one or more tiers formed by trees of different height and breed. The main breeds of boreal forests are pine, larch, spruce, silver fir, cedar, birch, aspen, oak, beech, and ash-tree. Forest canopy has a small density of 0.03…0.3 kg/m3, a big height of 2… 25 m, a small size of elements (branches and leaves), and relatively stable water content (gravimetric moisture). The wet biomass of a forest canopy varies from 0.2 to 1.2 kg/m2.
Table 1. Biometric features of agricultural vegetation.
|
Crop [reference] |
The number of plants per unit area N, 1/m2 |
Vegetation average height h, m |
Vegetation wet biomass Q, kg |
Vegetation gravimetric moisture m |
Vegetation water content per unit area W, kg |
|
Winter wheat [4] |
400 – 1000 |
0.6 – 1.12 |
0.2 – 1.3 |
0.5 – 0.85 |
0.25 – 1.1 |
|
Winter rye [4] |
330 – 700 |
1.2 – 1.5 |
0.2 – 0.45 |
0.5 – 0.84 |
|
|
Corn [4] |
5 – 30 |
1.2 – 3.2 |
|
0.81 – 0.84 |
|
|
Sugar beat [4] |
4 – 8 |
0.3 – 0.5 |
1.25 – 3 |
0.8 – 0.9 |
1.2 – 2.8 |
|
Corn [5] |
6 – 7 |
1.8 |
7 |
0.76 |
5.3 |
|
Alfalfa [5] |
|
0.6 |
2.2 |
0.82 |
1.8 |
|
Soybean [6] |
|
0.2 – 1.04 |
0.25 – 2.8 |
0.78 |
|
|
Corn [6]- |
|
2.6 |
5.5 |
|
|
|
Winter wheat [7] |
900 |
1.05 |
Volume fraction: Stalk – 0.00363 Heads – 0.01 |
Head – 0.45 Stalk – 0.63 Leaf – 0.16 |
|
|
Soybean [7] |
26 |
0.82 |
Volume fraction: 0.0282 |
Leaf – 0.76 Stalk – 0.81
|
|
|
Corn [8] |
Row spacing – 76 cm Average plant spacing – 19.8 cm |
2.7 |
Volume fraction: Stalk – 0.0035 Leaf – 0.00058 |
Volumetric moisture: Stalk – 0.47 Leaf – 0.65 |
|
|
Oat [9] |
180 – 440 |
1.35 |
6 |
0.7 – 0.86 |
|
|
Alfalfa [10] |
|
0.17 – 0.73 |
Data on volumetric water content w are presented |
|
0.23 – 1.95 |
|
Corn [10] |
|
0.3 – 2.7 |
|
0.2 – 10 |
|
|
Milo [10] |
|
0.3 – 1.17 |
|
0.66 – 10.9 |
|
|
Wheat [10] |
|
0.96 |
|
5.3 |
|
|
Tomato [11] |
7 – 10 |
|
7 – 15 |
|
|
The live soil cover is formed with bushes and shrubs, grass, moss, and lichen. Bushes have a height of 0.1…0.5 m and a wet mass of 0.1…0.5 kg/m2. The grass cover has a height up to 2 m and a wet mass of 0.05…0.5 kg/m2 with volumetric density of 0.2…1.0 kg/m3.
In the absence of live cover, a layer of dead needles, leaves, small branches, and bark is formed on the soil surface. This layer has a friable structure and a high speed of drying and moistening. The height of the layer is 0.01…0.07 m, its mass is 0.1…0.6 kg/m2, and its density is 5…30 kg/m3.
The density of a forest stand is described by the normal distribution
![]() ,
,
where ![]() is the distance between the trees,
is the distance between the trees, ![]() is the average distance between the trees,
is the average distance between the trees, ![]() where
where![]() is the coefficient of
variability of distance [12]. The height of a tree relates to its diameter in
accordance with an approximation
is the coefficient of
variability of distance [12]. The height of a tree relates to its diameter in
accordance with an approximation ![]() .
.
The crown diameter D, the crown length l, the height of crown widest part h0, and the height of crown beginning h, describes the canopy structure. These values are correlated and are connected to each other by known regression relations [12, 13].
An estimate of wet mass of tree components can be obtained due to a stable correlation between the trunk dimension and mass of leaves and branches [13, 15, and 16]. For example, the mass of leaves of 21 years old fir is given as
![]()
where g is the trunk cross section at the breast height. Similar relations are known for the mass of branches and trunks.
Tropical forests have some special features [14]. There is no dominated type of tree in this kind of forest. At a site of 1 ha there can be up to 100 different types of trees. They usually occupy 3-4 tiers. The single standing trees with height of 50…70 m form the upper tier; the main tier is formed by trees with not more than 35 m height and with dense canopy. Undergrowth is weak. Tropical forests have the greatest values of biomass up to 40…60 kg/m2.
Modeling the EM propagation in a forest requires a number of biometric parameters [1, 17-19]. Examples of forest parameters used in well known backscatter models are presented in Tables 2, 3. These parameters are in-situ measured and provide information on the biometrical features of some breeds of trees. Some data on biometric parameters of forest stands and their relationships and correlation can be found in [20-23, 83, 85, 86, 114, 150, and 159].
Table 2. Stand parameters for backscatter model simulation [1, 17, and 18]
|
Species |
Aspen |
Hemlock |
|
Stems/ha Height (m) Crown diameter (m) Crown length (m) DBH (cm) Branches/m3 Leaves/m3 Moisture content (% gravimetric) - trunks and branches - leaves |
1100 15 3.0 7.0 20 10 800
50 60 |
1100 15 3.0 7.0 20 105 196000
50 60 |
Table 3. Stand description and summary of MIMICS backscatter model [1, 19].
|
Forest type |
Red Pine & White Pine |
Maple/Beech |
|
Dry biomass (tons/ha) Total Apr-92 Jul-92 Trunk Branch Foliar Leaf Area Index (July) *Stems/ha (upper stratum) *Mean trunk height (m) *Mean trunk diameter (cm) *Mean crown thickness (m) *Crown layer geometry Leaves Thickness (cm) Length (cm) Mass (g) Density (no/m3) Primary branches Length (m) Diameter (cm) Mass/branch (g) Density (no/m3) Secondary branches Length (m) Diameter (cm) Mass/branch (g) Density (no/m3) Canopy moisture (% gravimetric) Trunk Apr-92 Jul-92 Leaves Apr-92 Jul-92 Branches Apr-92 Jul-92 *Orientation function Secondary branches Primary branches, uniform Laves, uniform Trunks |
182 83 152 22.4 8.3 6.4 1018 15.7 17.9 8.5
0.074 12.5 0.026 3838.5
0.73 0.99 23.4 7.49
0.33 0.57 3.5 25
57 50
65 65
57 50
0.5sin(q) 0.5sin(q) 0.5sin(q) 1.64cos(q8) |
203 206 157 45 3.3 3.89 925 16.1 17.5 7.4
0.1 6.4 0.37 118.1
2 1.5 189.4 2.14
1 0.75 23.7 8.6
46 48
- 57
46 50
1.23sin(q-30)9 0.5sin(q) 0.5sin(q) 1.64cos(q8) |
|
*Indicates parameters directly used in model |
||
1.2. The role and significance of attenuation by vegetation in remote sensing. What kind of attenuation is under the investigation?
Remote sensing of environment is based on retrieving algorithms that relate the environmental parameters (such as soil moisture, vegetation biomass, forest stem volume, and others) to the remotely sensed radiation characteristics (brightness temperature Tb, backscattering coefficient s0, and others). There are three general types of the retrieving algorithms. The first one uses the experimentally obtained regression relations between geophysical and radiation parameters. A disadvantage of this approach is a limited application (often, the regression relation can be used only within the test site or the region it was obtained). The second technique is based on the neural network approach and is being successfully developed for last years [24, 25]. For good results, this approach requires neural network training with statistically representative sampling that is not always possible. The third type of algorithms, which is most widely applied, uses the model approach [20, 26-40]. The models for radiation parameters mentioned above are being developed on the base of some theoretical assumptions about modeled object (vegetated soil, forests, and other) and are being specified and verified at the test sites under the control of geophysical parameters. The retrieving algorithms produce the inversion of radiation parameters into geophysical ones on the base of the developed models. Of course, this approach also has disadvantages. One of them is the influence of model error on the final result. Any modeling implies a simplification and idealization of a real object and, therefore, leads to the difference between the calculated and measured values of radiation parameters and to the error of geophysical parameters retrieving. Nevertheless, the model approach is still applied and developed due to its certain advantages. It makes it possible to understand the role of different object parameters in forming emission or backscattering, to estimate the sensitivity of radiation parameters to the change of geophysical parameters, to find out the possible dynamic range of radiation parameters change due to the change of geophysical parameters, to find and to analyze the spectral dependence of radiation parameters, and, then, to choose optimal frequencies for remote sensing. After this work, the model approach can be added by the first two mentioned algorithms to obtain the best results.
Brightness temperature (or backscattering coefficient) is a measure of intensity of radiation emitted (or backscattered) by the Earth’s surface. Therefore, the theory of radiation transfer is usually applied to model the emission and backscattering from vegetated terrain. This theory is a phenomenological one. The rigorous validation of its applicability to the case considered is not given (some words about it are said in [3]) and its applicability is grounded by a good agreement of model simulations with experimental results. The radiative transfer equation is not solved in the general case. The numerical solution of the equation [17-19, 41-46] is exact in that it includes all orders of multiple scattering. But this solution is inconvenient for experimentalists because of its complexity. It is also difficult to analyze and to understand the contribution of the different model parameters (see Tables 2 and 3) to the final result. By these reasons, simple analytical expressions for Tb and s0 are usually used which are either semi-empirical [40] or are derived from the radiative transfer equation on the basis of some simplifying assumptions (single scattering etc) [2,3]. These expressions are very convenient for calculations and analyses. Their accuracy is evaluated by comparing with a numerical solution of transfer equation [46, 47] and the error for Tb and s0 does not exceed 10 K and 2 dB, respectively that are comparable with the error of the model itself.
A zero-order solution of the radiative transfer equation for a vegetation covered soil can be written as a combination of three components [2, 3, 6, 48-50]
Tb = Tv(1 – r – q) + ksTsq + Tv(1 – r – q)(1 – ks)q (1)
where Tv is the vegetation temperature, Ts is the soil temperature, r is the reflectivity and q is the transmissivity of a vegetation layer, and ks is the emissivity of soil;
![]() (2)
(2)
where ![]() is
the backscatter of soil,
is
the backscatter of soil, ![]() is the backscatter of vegetation
half-space, and
is the backscatter of vegetation
half-space, and ![]() represents
the interaction term. More sophisticated models [1, 19, and 40] take into
account additional components for s0. Transmissivity q is usually
approximated by the expression
represents
the interaction term. More sophisticated models [1, 19, and 40] take into
account additional components for s0. Transmissivity q is usually
approximated by the expression ![]() , where
, where ![]() is the optical depth of the vegetation
layer,
is the optical depth of the vegetation
layer, ![]() is the
viewing angle. Transmissivity of the vegetation layer determines the canopy
attenuation (
is the
viewing angle. Transmissivity of the vegetation layer determines the canopy
attenuation (![]() )
and is very important and significant in remote sensing of vegetated terrain
due to the following reasons.
)
and is very important and significant in remote sensing of vegetated terrain
due to the following reasons.
Attenuation by vegetation strongly depends on the frequency. At high frequencies (X-band) attenuation is large and the brightness temperature and the backscattering coefficient relate to these values for the vegetation layer only. It allows crop classification by radar [1, 51], crop state monitoring by radar [52] and by microwave radiometry [5, 53, and 54]. At low frequencies (L-band) attenuation is not so big and that enables researchers to estimate soil parameters using linear regressions [55] or simple procedures [11].
Knowledge of spectral dependence of attenuation gives a possibility of multi channel (multi frequency) measurements of radiation parameters with inversion of measured data into, for example, soil moisture and vegetation water content [28, 29, 35-38].
For forest vegetation, the attenuation determines the penetration capability of radar sounding [1] and the possibility of objects detection beneath the forest canopy.
In radio communication the attenuation of the coherent field and its spectral dependence is of great interest [56] since it determines the capability of communication links. It follows therefore that investigations of attenuation spectrum of vegetation are of great importance and actuality.
1.3. General approach for EM waves propagation in vegetation.
The investigation of EM wave’s propagation, attenuation, emission,
and scattering in vegetation canopies meets some difficulties. From a
theoretical point of view vegetation canopies are principally random media with
inhomogeneities of varying forms and dimensions. In the frequency band of
interest the dimensions of leaves and stalks, brunches and trunks are
comparable with the wavelength making it extremely difficult to model
propagation in such a medium due to the required application of diffraction
theory to examine the scattering by a single inhomogeneity. A rigorous
theoretical solution of the EM propagation problem for a vegetation layer is
very complicated (if possible at all). Due to this reason approximate models
have to be used. These models either treat vegetation as a collection of randomly
distributed lossy scatterers (discrete approach) or they consider the canopy as
a slab with random dielectric permittivity (continuous approach). In order to
understand the relation between these two conceptually different approaches and
to determine the limits of their validity the problem of EM propagation in
vegetation should be considered from the position of random media propagation
theory [3]. The electric field ![]() in a random medium is given by the
integral equation [57]
in a random medium is given by the
integral equation [57]
![]() (3)
(3)
![]() is the
incident field,
is the
incident field, ![]() is
the wave number in free space (
is
the wave number in free space (![]() ),
), ![]() is the random dielectric permittivity, and
is the random dielectric permittivity, and
![]() is the free
space dyadic Green’s function. To obtain the moments of the field the multiple
scattering series is derived from (3), and, then, this series is averaged that
leads to the Dyson equation for the mean field and the Bethe-Salpeter equation
for the covariance. The principal point of the theory is the appropriate choice
of the initial field inside the inhomogeneity in the multiple scattering
series. The formal approach for the continuous case gives
is the free
space dyadic Green’s function. To obtain the moments of the field the multiple
scattering series is derived from (3), and, then, this series is averaged that
leads to the Dyson equation for the mean field and the Bethe-Salpeter equation
for the covariance. The principal point of the theory is the appropriate choice
of the initial field inside the inhomogeneity in the multiple scattering
series. The formal approach for the continuous case gives
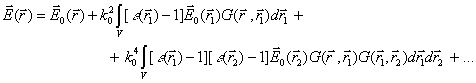 (4)
(4)
It is important to emphasize that the integration in (3) for a truly
discrete medium (like vegetation, for example) is to be performed only over
those volume elements where ![]() , i.e. the elements of the scatterers.
Hence, separating the volumes of scatterers expression (3) can be rewritten as
, i.e. the elements of the scatterers.
Hence, separating the volumes of scatterers expression (3) can be rewritten as
![]() (5)
(5)
where the index i indicates that this value is related to the i-th
scatterer; N is the total number of scatterers. For the field ![]() inside i-th
scatterer it can be obtained from (5)
inside i-th
scatterer it can be obtained from (5)
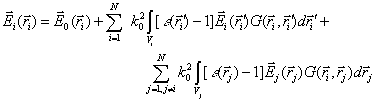 (6)
(6)
From equations (5) and (6) the multiple scattering series can be written by substituting (6) into (5) and iterating this process
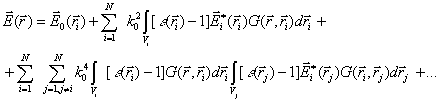 (7)
(7)
In (7) ![]() is the field inside the isolated
scatterer which is given by the scattering operator
is the field inside the isolated
scatterer which is given by the scattering operator
![]() (8)
(8)
One can see that in the discrete approach due to the separation of particle volumes the multiple scattering series begins with the field inside the isolated inhomogeneity. Of course, this field has to be known but it can be found from the solution of the diffraction problem.
It is interesting to find out [3] when the continuous and the
discrete approaches coincide. It is clear from (4), (7), and (8) that this is
the case when the scattering operator of an isolated particle may be
represented by the Born series (weak scatterers). It is seen from (8) that this
is valid under the following conditions. The first is: ![]() ; this corresponds to the Rayleigh–Gans
scattering by particles and to the theory of small perturbations of continuous
media. The second is:
; this corresponds to the Rayleigh–Gans
scattering by particles and to the theory of small perturbations of continuous
media. The second is: ![]() where
d is the characteristic size of the scatterer (for example, leaf
thickness); this corresponds to Rayleigh scattering for particles and to the
strong fluctuations theory for the continuous case.
where
d is the characteristic size of the scatterer (for example, leaf
thickness); this corresponds to Rayleigh scattering for particles and to the
strong fluctuations theory for the continuous case.
If the scatterer is strong the formal Born series obtained from (8) may not converge and the application of the continuous approach to the discrete media makes no sense. From the sufficient condition
![]() (9)
(9)
one can estimate the limits of validity of the continuous approach for
vegetation. For leaves d ~ 0.2 mm (leaf thickness of the most crops and trees), e ~ 20 and taking ![]() one has l ~ 8 cm. This implies that
both models may be successfully applied for modeling vegetation up to the
C-band. For higher frequencies the use of the discrete approach is more
correct.
one has l ~ 8 cm. This implies that
both models may be successfully applied for modeling vegetation up to the
C-band. For higher frequencies the use of the discrete approach is more
correct.
2. The model of vegetation as a continuous medium.
2.1. EM waves propagation in a random continuous medium.
In the continuous approach the vegetation is described by the
effective permittivity tensor ![]() . In [7, 8, 31, and 58] authors used
formulas for
. In [7, 8, 31, and 58] authors used
formulas for ![]() obtained
for mixture of dielectrics in the electrostatic approach. In [64] the
continuous medium concept is used to find the attenuation by foliage. The wave
corrections for
obtained
for mixture of dielectrics in the electrostatic approach. In [64] the
continuous medium concept is used to find the attenuation by foliage. The wave
corrections for ![]() were
derived in [59-61] on the basis of small perturbation theory. The vector
problem which has to take into account the singularity of the Green’s function
was considered in [62, 63] using the results of strong fluctuation theory.
were
derived in [59-61] on the basis of small perturbation theory. The vector
problem which has to take into account the singularity of the Green’s function
was considered in [62, 63] using the results of strong fluctuation theory.
In the latter case the dyadic Green’s function is decomposed into a principal value part and a Dirac delta function part [57, 62, and 63]
![]() (10)
(10)
where P.S. stands for the principal value and R is a constant uniaxial matrix. Then new variables are introduced
 (11)
(11)
where ![]() and
and
![]() is a
deterministic uniaxial permittivity tensor (quasistatic part of
is a
deterministic uniaxial permittivity tensor (quasistatic part of ![]() ) which is to be chosen
such that the contribution of the singularity term of the dyadic Green’s
function cancels, and I is the unit matrix. The integral equation in the
new variables is used to find the mean field by conventional methods [57, 62,
and 63]. The tensor
) which is to be chosen
such that the contribution of the singularity term of the dyadic Green’s
function cancels, and I is the unit matrix. The integral equation in the
new variables is used to find the mean field by conventional methods [57, 62,
and 63]. The tensor ![]() is
determined from the condition
is
determined from the condition ![]() where brackets denote ensemble averaging.
In the low frequency limit the effective permittivity is given by
where brackets denote ensemble averaging.
In the low frequency limit the effective permittivity is given by
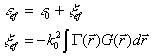 (12)
(12)
where ![]() is
the correlation function of
is
the correlation function of ![]() .
.
The results of strong fluctuation theory stated above were applied
to find the effective permittivity of vegetative media in [62, 63]. The success
of determining ![]() depends
on the appropriate choice of matrix R that allows canceling completely
the singularity of the Green’s function. In [62] it was chosen in such a way that
the frequency independent terms of
depends
on the appropriate choice of matrix R that allows canceling completely
the singularity of the Green’s function. In [62] it was chosen in such a way that
the frequency independent terms of ![]() would equal to zero. In
this case
would equal to zero. In
this case ![]() represents only wave corrections to
the static part of the effective permittivity. In [63] it was shown that it is
expedient to find the matrix R considering the electrostatic problem for
inhomogeneity of the medium. The inhomogeneities in form of discs and needles
were considered. The following expressions for the static part of effective
permittivity have been found:
represents only wave corrections to
the static part of the effective permittivity. In [63] it was shown that it is
expedient to find the matrix R considering the electrostatic problem for
inhomogeneity of the medium. The inhomogeneities in form of discs and needles
were considered. The following expressions for the static part of effective
permittivity have been found:
a. Thin chaotic discs
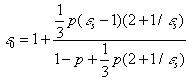 (13)
(13)
where ![]() is the permittivity of
the scatterer and p is the fractional volume occupied by discs
(vegetation volume density).
is the permittivity of
the scatterer and p is the fractional volume occupied by discs
(vegetation volume density).
b. Thin chaotic needles
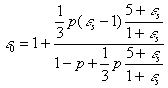 (14)
(14)
c.
Thin
vertical needles (here ![]() )
)
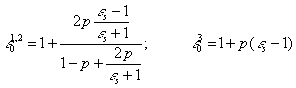 (15)
(15)
When p << 1 (see Table 1; p is less than 0.01) and ![]() >> 1 the above
expressions reduce to the form that often used by experimentalists
>> 1 the above
expressions reduce to the form that often used by experimentalists
![]() (Chaotic discs);
(16)
(Chaotic discs);
(16)
![]() (Chaotic needles)
(17)
(Chaotic needles)
(17)
![]() (Vertical needles)
(18)
(Vertical needles)
(18)
It is shown in [3, 63] that the wave corrections to ![]() corresponds to the
scattering of Rayleigh particles and in the case of small scatterers the
continuous and the discrete approaches provide analogous results for
attenuation. The advantage of the continuous model is that it provides
corresponds to the
scattering of Rayleigh particles and in the case of small scatterers the
continuous and the discrete approaches provide analogous results for
attenuation. The advantage of the continuous model is that it provides ![]() for dense (p ~ 1) media (for example,
snow), while the discrete model is applied for sparse media.
for dense (p ~ 1) media (for example,
snow), while the discrete model is applied for sparse media.
2.2. Effective dielectric constant of vegetation.
Expressions (13) – (18) were used by researchers to calculate the effective dielectric constant of vegetation and the values connected with it.
In work by Du and Peake [65], attenuation properties of foliage
media in UHF-band were calculated using ![]() concept for p = 0.001-0.005 and
concept for p = 0.001-0.005 and ![]() where
where ![]() is the dielectric
constant of saline water contained in leaves at the ionic conductivity values
of (2…4)×10-3 Ohm-1 cm-1. Reflection
from vegetation canopies at small sliding angles was calculated in [66] using Fresnel
formulas and expressions (16), (17). Tensor of dielectric permittivity of
foliage media was derived in [67] where the data on conductivity and on volume
fraction of vegetation are presented. The effective dielectric constant of
foliage was calculated in [68] using data from [67]. Effective dielectric
constant was calculated in [7] for wheat and soybean and in [8] for corn. In works
[64, 70], the effective dielectric constant of foliage is calculated for
spherical inhomogeneities. In papers [71, 69], the effective dielectric
constant of vegetation is modeled by the expression
is the dielectric
constant of saline water contained in leaves at the ionic conductivity values
of (2…4)×10-3 Ohm-1 cm-1. Reflection
from vegetation canopies at small sliding angles was calculated in [66] using Fresnel
formulas and expressions (16), (17). Tensor of dielectric permittivity of
foliage media was derived in [67] where the data on conductivity and on volume
fraction of vegetation are presented. The effective dielectric constant of
foliage was calculated in [68] using data from [67]. Effective dielectric
constant was calculated in [7] for wheat and soybean and in [8] for corn. In works
[64, 70], the effective dielectric constant of foliage is calculated for
spherical inhomogeneities. In papers [71, 69], the effective dielectric
constant of vegetation is modeled by the expression
![]() (19)
(19)
with ![]() (linear
model),
(linear
model), ![]() (refractive
model), and
(refractive
model), and ![]() (cubic
model). The best results are found for the refractive mixing model. In paper [72],
formulas (17), (18) were used to calculate the attenuation in forest canopy. Unfortunately,
data on the direct measurements of the effective dielectric constant of
vegetation were not found. In the works mentioned above
(cubic
model). The best results are found for the refractive mixing model. In paper [72],
formulas (17), (18) were used to calculate the attenuation in forest canopy. Unfortunately,
data on the direct measurements of the effective dielectric constant of
vegetation were not found. In the works mentioned above ![]() was used to calculate the
attenuation (or the reflection). Calculated values of attenuation (reflection) were
in good agreement with measured ones. It shows a capability of the continuous
concept in vegetation modeling.
was used to calculate the
attenuation (or the reflection). Calculated values of attenuation (reflection) were
in good agreement with measured ones. It shows a capability of the continuous
concept in vegetation modeling.
Data on the effective dielectric constant of vegetation given by researchers are presented in Table 4. One can see that because the vegetation is very a sparse medium the effective dielectric constant is only slightly differs from the unit. It provides the very low (negligible) values of reflection coefficient at the near to nadir angle. Reflection is significant only at small sliding angles. At the same time the reflectivity of a vegetation layer can achieve the values of 0.05…0.15 [2] due to the scattering by the plant elements. In the continuous approach the scattering effects are neglected since the size of scatterers is proposed very small compared with wavelength. This circumstance places a limit (as it was mentioned) on the continuous approach applicability.
Table 4. Effective dielectric constant of vegetation.
|
Vegetation type |
Frequency band |
Effective dielectric constant |
|
Wheat stalks [7] |
X-band (10.2 GHz) |
1.036 + j0.01644 ( 1.006 + j0.00042 ( |
|
Soybean [7] |
X-band (10.2 GHz) |
1.038 + j.01707 |
|
Coniferous forest [68] |
L-band (1.4 GHz) |
(1.00095…1.0028) + j(0.00019…0.014) |
|
Deciduous forest [68] |
L-band (1.4 GHz) |
(1.0028…1.19) + j(0.00058…0.038) |
|
Foliage [70] |
50 MHz 200 MHz 500 MHz 800 MHz 1300 MHz |
1.03 + 0.00073 1.03 + 0.00046 1.03 + 0.00028 1.03 + 0.00021 1.03 + 0.00020 |
3. The model of vegetation as a collection of scatterers (discrete model).
3.1. EM waves propagation in a random discrete medium.
The discrete model was applied in [8, 17-20, 40-45, 47, 48, 75-91] to find the propagation and scattering characteristics of vegetation canopies. To understand some peculiarities of the discrete approach the main results of the theory of wave propagation through discrete random media should be considered [88-90, 3].
The propagation of the mean field through such a medium may be described by the dispersion equation for the wave number [88]
![]() (20)
(20)
where ![]() is
the Fourier transform of the mass operator of the Dyson equation for the mean
field. Based on Finkelberg’s approach [88]
is
the Fourier transform of the mass operator of the Dyson equation for the mean
field. Based on Finkelberg’s approach [88]
![]() (21)
(21)
where ![]() is
the s-point correlation function and Ts is the
scattering operator for a system of s scatterers located at the points
is
the s-point correlation function and Ts is the
scattering operator for a system of s scatterers located at the points ![]() . For independent scatterers
. For independent scatterers ![]() and
and
![]() (22)
(22)
where n is the number density of scatterers and T1
is the scattering operator of one isolated scatterer. This is the Foldy-Twersky
approach for independent point scatterers. The substitution of ![]() in the dispersion
equation by
in the dispersion
equation by ![]() signifies
neglecting spatial dispersion of the mean field and leads to the radiative
transfer equation for the field coherence function. It is valid when
signifies
neglecting spatial dispersion of the mean field and leads to the radiative
transfer equation for the field coherence function. It is valid when
![]() (23)
(23)
Under this condition dispersion equation can be approximated as
![]() (24)
(24)
In this case (fare-zone approximation) EM parameters of a discrete media are determined by scattering and extinction of electromagnetic wave by a single scatterer. The field scattered by the scatterer in the far-zone is given as [89]
![]() (25)
(25)
where ![]() is
the complex scattering amplitude. The extinction cross section
is
the complex scattering amplitude. The extinction cross section ![]() and scattering cross
section
and scattering cross
section ![]() of
the scatterer are found from the expressions
of
the scatterer are found from the expressions
![]() =
= ![]() (26)
(26)
![]() (27)
(27)
where ![]() is
a unit vector defining the polarization of incident wave,
is
a unit vector defining the polarization of incident wave, ![]() is the element of solid angle,
and Im denotes the imaginary part. The absorption cross section
is the element of solid angle,
and Im denotes the imaginary part. The absorption cross section ![]() is determined by the Ohmic
losses of the field
is determined by the Ohmic
losses of the field ![]() inside
the scatterer
inside
the scatterer
 (28)
(28)
where ![]() is
the imaginary part of scatterer dielectric permittivity. According to the optic
theorem
is
the imaginary part of scatterer dielectric permittivity. According to the optic
theorem
![]() (29)
(29)
Parameters of the transfer theory are the extinction coefficient ![]() , the single scattering albedo
, the single scattering albedo
![]() , and phase
function
, and phase
function ![]() . These
values are given by the expressions
. These
values are given by the expressions
![]() ,
, ![]() ,
(30)
,
(30)
and 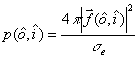 (31)
(31)
Practically, considering the discrete model as applied to
vegetation canopies, all studies used the radiative transfer theory. The
applicability of transfer theory is theoretically proved for the case when the
individual scatterers are located in the far zone of each other [90]. In this
case the extinction is a linear function of the number density (neglecting
correlation between particle positions). It is shown in [3, 73-74] that it is
valid for the vegetation canopies with fractional volume density ![]() . For dense vegetation
the “dense medium radiative transfer theory” [91] or “dense medium phase and
amplitude correction theory” [87] can be applied.
. For dense vegetation
the “dense medium radiative transfer theory” [91] or “dense medium phase and
amplitude correction theory” [87] can be applied.
3.2. Attenuation and scattering of EM waves by plant elements.
3.2.1. Theoretical models.
Electrodynamic parameters of vegetation media in the discrete
model is characterized by the scattering operator (or scattering amplitude, or
scattering and extinction cross sections ![]() and
and ![]() , respectively) of a single scatterer and,
hence, it is important to examine scattering and extinction by different
individual plant elements. The sizes of leaves, stalks, branches, and trunks in
the frequency band of interest are comparable with the wavelength (resonance
region) and, therefore, the scattering and extinction cross sections must be
calculated from diffraction models that take into account the shape and size of
a plant element as precisely as possible. Since the elements of plants are
similar in shape to flat discs, strips (leaves), and cylinders (stalks,
branches, and trunks), the diffraction problems for bodies with the above
shapes are usually discussed. Known solutions for perfectly conducting
infinitely thin disc and strip are not applicable to find the emissivity of
vegetation layer because the last is determined by the active losses in a
medium (but they may be useful in calculating scattering from vegetation [92]).
The solutions of the diffraction problems for dielectric discs and strips are
not known. In this case the cross sections
, respectively) of a single scatterer and,
hence, it is important to examine scattering and extinction by different
individual plant elements. The sizes of leaves, stalks, branches, and trunks in
the frequency band of interest are comparable with the wavelength (resonance
region) and, therefore, the scattering and extinction cross sections must be
calculated from diffraction models that take into account the shape and size of
a plant element as precisely as possible. Since the elements of plants are
similar in shape to flat discs, strips (leaves), and cylinders (stalks,
branches, and trunks), the diffraction problems for bodies with the above
shapes are usually discussed. Known solutions for perfectly conducting
infinitely thin disc and strip are not applicable to find the emissivity of
vegetation layer because the last is determined by the active losses in a
medium (but they may be useful in calculating scattering from vegetation [92]).
The solutions of the diffraction problems for dielectric discs and strips are
not known. In this case the cross sections ![]() and
and ![]() can be found only under some restrictive
assumption between the size of an element and the wavelength. The following
models were used.
can be found only under some restrictive
assumption between the size of an element and the wavelength. The following
models were used.
a. Small particles (low-frequency asymptotic case).
A general formulation for the scattered field ![]() can be obtained via the Helmholtz
integral equation. For a scatterer located at the origin, the Helmholtz
integral equation relates the far zone scattered field to the field inside the
scatterer
can be obtained via the Helmholtz
integral equation. For a scatterer located at the origin, the Helmholtz
integral equation relates the far zone scattered field to the field inside the
scatterer ![]() through
the relation [3, 93-98]
through
the relation [3, 93-98]
![]() (32)
(32)
where ![]() is
the unit dyad and
is
the unit dyad and ![]() is
the observation direction. For small spheroid
is
the observation direction. For small spheroid
![]() =
= ![]() (33)
(33)
where ![]() is
the polarizability tensor and
is
the polarizability tensor and ![]() is the incident wave at a given point.
is the incident wave at a given point.
For a small disc and for the principle directions [97]
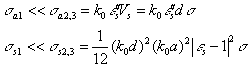 (34)
(34)
where d is the thickness, a is the radius, and ![]() is the area of the
disc.
is the area of the
disc.
b. Very large plane particles (high-frequency case).
The absorption and scattering cross sections of such particles can
be expressed, neglecting edge effects, in terms of the reflection coefficient ![]() and the transmission
coefficient
and the transmission
coefficient ![]() of
an infinite layer of the same thickness [97, 99]
of
an infinite layer of the same thickness [97, 99]
![]() (35)
(35)
For ![]() , a
condition that is satisfied for leaves up to the X-band, when the wave is
normally incident upon the layer [97]
, a
condition that is satisfied for leaves up to the X-band, when the wave is
normally incident upon the layer [97]
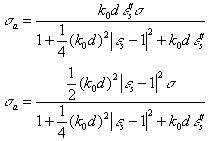 (36)
(36)
c. Plane thin particles (resonance case).
This problem is considered in [94, 97, and 100] with the use of generalized Rayleigh-Gans approximation. When the wave vector of the incident wave is normal to the plane of the particle it was found for discs [97, 100]
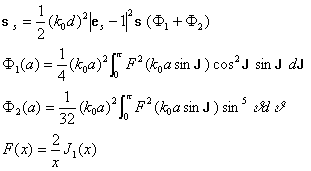 (37)
(37)
where ![]() is
the Bessel function of the first order. These expressions reduce to the case of
small disc with
is
the Bessel function of the first order. These expressions reduce to the case of
small disc with ![]() .
The results for arbitrary incidence and polarization one can find in [94].
.
The results for arbitrary incidence and polarization one can find in [94].
d. Dielectric cylinders.
The relationships for the extinction and scattering cross sections of a cylinder can be found in [8, 94, 97, 100, 101, and 102]. As a rule, the solution of diffraction problem for infinite cylinder first given by Wait [105, 106] for arbitrary incident angle is used. The calculations and experiments have shown that in this case the effect of resonance extinction and scattering are significant [8, 94, and 100].
3.2.2. Experimental data.
Actually, there are rather few papers where experimental data on microwave scattering and absorption by pant elements are presented. Passive (radiometric) and active (radar) methods were used to measure the extinction, scattering, and backscattering cross sections of leaves, stalks, and brunches.
Measurements of the attenuation loss for horizontally polarized and vertically polarized waves transmitted through a fully grown corn canopy, and of the phase difference between the two transmitted waves were conducted in [8] at frequencies of 1.62, 4.75, and 10.2 GHz. The measurements were made at incidence angles of 20°, 40°, 60°, and 90° relative to the normal incidence. Experimental data were compared with computed ones which were based on a model of infinite cylinders (stalks) and randomly oriented discs (leaves). The proposed model was suitable for corn-like canopies.
Measurements of backscattering from leaves were conducted in [92, 94]. In [94] the disc and finite cylinder models based on the generalized Rayleigh-Gans approximation were compared with measurements of backscattering cross sections for an aspen leaf and a birch stick. There was a good agreement between the theory and the measurement except of small incident angles for stick that was explained by possible diffraction from the stick ends (the model considers the inner field equaled to the field inside an infinite cylinder; this was first noted in [100] where the diffraction problem at the end of circular cylinder was discussed and additional extinction due to the diffraction at the end of cylinder was calculated).
Propagation in simulated canopies composed of bare deciduous twigs and leafy coniferous brunches was investigated at 9 GHz [103] and interpreted [104] upon the Foldy-Lax theory for coherent wave propagation through a sparsely discrete random medium. The infinite cylinder scattering function was applied. A good agreement was obtained between the model and attenuation observations.
A radiometric method was proposed in [107] to measure the transmissivity and the reflectivity of leaves at frequencies 21, 35, and 94 GHz. Different kinds of crops and trees leaves were investigated. The model of an infinite flat dielectric sheet (very large plane particle) was in good agreement with the measurement and was used to examine the dielectric behavior of leaves in the frequency band reported.
The radiometric method was also applied to measure the extinction and scattering cross sections of leaves and branches at frequencies of 1, 1.67, and 13.3 GHz [97, 100]. Dependencies of the cross sections on the leaves and brunches dimensions were investigated. The experimental results were compared with theoretical ones obtained for the models introduced above.
Analysis of data of the numbered investigations enables one to make the following conclusions.
The general behavior of EM extinction and scattering by leaves is
well described by the thin plane particle model (the generalized Rayleigh-Gans
approximation) at frequencies below S-band. This model is successfully applied
in known backscatter MIMICS and Santa Barbara models for vegetation [18, 19]. At centimeter wavelengths,
the resonance attenuation and scattering (appearing when the leaf dimension is
comparable with the wavelength) is significant [3, 97]. In this frequency range
further development of models is required to evaluate the extinction and the
scattering by leaves. For ![]() (a is the width of a leaf in the
form the of a strip, and D is the diameter of a round leaf) the large
plane particle model can be applied. The long cylinder model is a satisfactory
one for calculating
(a is the width of a leaf in the
form the of a strip, and D is the diameter of a round leaf) the large
plane particle model can be applied. The long cylinder model is a satisfactory
one for calculating ![]() and
and
![]() of stems and
branches when their length
of stems and
branches when their length ![]() . For
. For ![]() , the small (Rayleigh’s) particles model
can be used. When
, the small (Rayleigh’s) particles model
can be used. When ![]() ,
resonance effects of extinction can be significant [97, 100].
,
resonance effects of extinction can be significant [97, 100].
4. Dielectric properties of vegetation constituents.
4.1. Theoretical models.
The dielectric constant of
vegetation material is a significant point of the theory. This value is
governed by water content and salinity of plant elements. Despite its
fundamental importance, however, the dielectric behavior of vegetation material
is not well understood in the frequency band considered. The dielectric mixture
models to relate the dielectric constant ![]() of vegetation to the dielectrics of its
constituents – the bulk vegetation material and liquid water – changed from
quite simplistic forms [60] capable of providing approximate estimates at best
to complicated ones such as the dual-dispersion model [108], for example.
of vegetation to the dielectrics of its
constituents – the bulk vegetation material and liquid water – changed from
quite simplistic forms [60] capable of providing approximate estimates at best
to complicated ones such as the dual-dispersion model [108], for example.
The simplest approximation for the dielectric constant was proposed by Peake [75] and was used by many researchers. It reads
![]() (38)
(38)
where ![]() is
the relative complex dielectric constant of water. The relative complex
dielectric constant of saline water is given by the Debye relaxation equation
[108]
is
the relative complex dielectric constant of water. The relative complex
dielectric constant of saline water is given by the Debye relaxation equation
[108]
![]() (39)
(39)
where ![]() and
and
![]() are the
static and high-frequency limits of
are the
static and high-frequency limits of ![]() ,
, ![]() = 8.854´10-12 F×m-1 is the
permittivity of free space, f is the frequency in hertz, and s is the ionic conductivity
of the aqueous solution in siemens per meter. Conductivity value is determined
by salinity S of the solution. The salinity is defined as the total mass
of solid salt in grams dissolved in 1 kg of solution and is expressed in parts
per thousand (o/oo) on a weight basis. The relation of the model
parameters to the temperature and the salinity of the solution can be found,
for example, in [113].
= 8.854´10-12 F×m-1 is the
permittivity of free space, f is the frequency in hertz, and s is the ionic conductivity
of the aqueous solution in siemens per meter. Conductivity value is determined
by salinity S of the solution. The salinity is defined as the total mass
of solid salt in grams dissolved in 1 kg of solution and is expressed in parts
per thousand (o/oo) on a weight basis. The relation of the model
parameters to the temperature and the salinity of the solution can be found,
for example, in [113].
In work [109], different dielectric mixing models were examined to
fit experimental data on the dielectric constant of wheat and corn leaves and
stalks. The propagation (refractive) two-phase model, the random-needle
two-phase model, the random-disc two-phase model, the three-component
random-needle model (accounting for “depressed” value of ![]() due to an action of suction forces [110]), and the
four-phase refractive model (where the water was subdivided into a bound-water
component and a free-water component; bound water refers to water
molecules that are tightly held to organic compounds by physical forces, and
free water refers to water molecules that can move within the material with
relative ease) were considered. The free-water component is assigned the
dielectric properties of bulk water (the Debye equations) and the bound-water
component is assumed to have dielectric properties similar to those of ice. It
was noted in [109] that until further work is performed to better determine the
roles of free and bound water in heterogeneous materials, it will not be
possible to uniquely specify a dielectric mixing model for a vegetation-water
mixture.
due to an action of suction forces [110]), and the
four-phase refractive model (where the water was subdivided into a bound-water
component and a free-water component; bound water refers to water
molecules that are tightly held to organic compounds by physical forces, and
free water refers to water molecules that can move within the material with
relative ease) were considered. The free-water component is assigned the
dielectric properties of bulk water (the Debye equations) and the bound-water
component is assumed to have dielectric properties similar to those of ice. It
was noted in [109] that until further work is performed to better determine the
roles of free and bound water in heterogeneous materials, it will not be
possible to uniquely specify a dielectric mixing model for a vegetation-water
mixture.
To determine the dielectric dispersion properties of bound water, measurements were made [108] for sucrose-water solution of known volume ratios. On this basis the Debye-Cole dual-dispersion model was proposed by Ulaby and El-Rayes and was found to give excellent agreement with experimental data for corn leaves and stalks over the entire 0.2…20 GHz frequency range [108].
The three component model has the form
![]() (40)
(40)
where ![]() and
and
![]() are the
dielectric constants of free and bound water, respectively;
are the
dielectric constants of free and bound water, respectively; ![]() is the volume fraction of free
water,
is the volume fraction of free
water, ![]() is the
volume fraction of the bulk vegetation – bound water mixture. At room
temperature (T = 22°C) and salinity
is the
volume fraction of the bulk vegetation – bound water mixture. At room
temperature (T = 22°C) and salinity ![]() o/oo
o/oo ![]() is given by [108]
is given by [108]
![]() (41)
(41)
where f is in gigahertz and s (the ionic conductivity
of the free water solution) is in siemens per meter. One of the unknown
properties of the mixture is the water distribution between free and bound
fractions. The magnitudes of ![]() and s and their variations with
the gravimetric moisture content
and s and their variations with
the gravimetric moisture content ![]() were determined in [108] by fitting the
model to the measured data of
were determined in [108] by fitting the
model to the measured data of ![]() . For green leaves (
. For green leaves (![]() =0.6…0.7) volume fractions of
free water and bound water (
=0.6…0.7) volume fractions of
free water and bound water (![]() [108]) occurred to be approximately equal.
In general, it was proposed in [111] that most water is in a bound state when
the water content of vegetation is low, and the fraction of free water
increases with increasing water content. For example, the amount of free water
for green leaves varies from 20% to 40% of total saturated weight, while the
amount of bound water varies from 15% to 40%. In young xylem tissue [111], free
water represents about 51% of the stem volume and reduces to 1% in wood older
than 40 years. The amount of bound water is around 12% - 13% and remains
essentially unchanged with age.
[108]) occurred to be approximately equal.
In general, it was proposed in [111] that most water is in a bound state when
the water content of vegetation is low, and the fraction of free water
increases with increasing water content. For example, the amount of free water
for green leaves varies from 20% to 40% of total saturated weight, while the
amount of bound water varies from 15% to 40%. In young xylem tissue [111], free
water represents about 51% of the stem volume and reduces to 1% in wood older
than 40 years. The amount of bound water is around 12% - 13% and remains
essentially unchanged with age.
One can see that the apportionment of water between bound and free states is a critical point of the model. Relations, which related the volume fractions of free and bound water to the gravimetric moisture content and which were found in [108] for corn, can not be valid for forest vegetation, for example.
Another critical point is that the model makes assumptions about the organic material which may not be appropriate for forest constituents, for instance, for forest litter [112]. In particular, the dual-dispersion model, which is used to model corn leaves, assumes that the water in the organic material is composed of two parts, some of which is free and the rest is molecularly bound to sucrose sugar. While this model is more than adequate for corn leaves, other sugars may predominate in aspen and pine, for example [112]. As a result, bound water can demonstrate other dispersion characteristics.
The dual-dispersion model was used in a number of radar backscatter experiments on forests to derive complex permittivity values. Some researchers use more straightforward approach i.e. direct dielectric measurements on trunks, branches, and needles [114].
A semi-empirical formula for ![]() was developed in [115, 116] for broad
leaves of different plants. The explicit parameters are the dry-matter
fraction,
was developed in [115, 116] for broad
leaves of different plants. The explicit parameters are the dry-matter
fraction, ![]() =
(dry mass)/(fresh mass), of the leaf and the complex permittivity of saline
water
=
(dry mass)/(fresh mass), of the leaf and the complex permittivity of saline
water ![]() . Implicit parameters are
temperature, salinity, and frequency as determining
. Implicit parameters are
temperature, salinity, and frequency as determining ![]() . For most plants the salinity was assumed close to 1
o/oo (that is several times less than in [108, 109]). The formula is
applicable in the frequency band of 1…100 GHz to fresh leaves; their
. For most plants the salinity was assumed close to 1
o/oo (that is several times less than in [108, 109]). The formula is
applicable in the frequency band of 1…100 GHz to fresh leaves; their ![]() value is in the range
0.1…0.5 while their density is near 1 g/cm3. The explicit form for
value is in the range
0.1…0.5 while their density is near 1 g/cm3. The explicit form for ![]() is given by
is given by
![]() (42)
(42)
The simplicity of the equation and its validity over a large frequency range makes this formula attractive for the electromagnetic modeling of vegetation canopies.
4.2. Experimental data.
An extensive study of dielectric properties of vegetation materials started from works [109, 117]. In work [109], three waveguide transmission systems were used to measure the magnitude and phase of the field transmission coefficient of the sample contained in the sample holder. The sample holder was filled with chopped vegetation material. The relative complex dielectric constant of the sample was determined from measurements of the transmission coefficient and, then, was recalculated into the dielectric constant of vegetation material using the simple propagation (refractive) model. The dielectric data reported in [117] were based on measurements of the amplitude and phase of the reflection coefficient of a coaxial probe terminated in the material under test. To avoid the difficulties with measurements of thin materials a technique was developed that included measurements of the input admittance when the probe is terminated with a thin dielectric slab placed against a background consisting of an electrically thick material with known dielectric constant.
The coaxial probe technique was developed further to design an Applied Microwave Corporation Field Portable Dielectric Probe (PDP) [111, 114, and 118]. Appearance of PDP allowed a set of extensive in situ and in vivo measurements of the complex permittivity of tree material [119-126, 111, and 114]. Some experimental data can be found also in [116, 127, and 128].
The relationship between
xylem tissue dielectric constant, xylem sap flux density, and xylem sap chemical
composition as measured in the stems of two Norway spruce was examined in [111]
at frequency of 0.5 GHz. It was shown that spatial and temporal variability in the
xylem tissue dielectric constant is influenced not only by water content, but
by variations in xylem sap chemistry as well. For tree A the real part of ![]() changed along the trunk
height in the limits of 6…11; the imaginary part of
changed along the trunk
height in the limits of 6…11; the imaginary part of ![]() changed along the trunk height
in the limits of 1…2. The temporal variations of
changed along the trunk height
in the limits of 1…2. The temporal variations of ![]() and
and ![]() did not exceed 2 and 0.5 units,
respectively. For tree B the real part of
did not exceed 2 and 0.5 units,
respectively. For tree B the real part of ![]() changed along the trunk height in the
limits of 7…22; the imaginary part of
changed along the trunk height in the
limits of 7…22; the imaginary part of ![]() changed along the trunk height in the
limits of 0…4. The temporal variations of
changed along the trunk height in the
limits of 0…4. The temporal variations of ![]() and
and ![]() did not exceed 6…14 and 2 units,
respectively. The correlation between dielectric properties and water regime
and sap chemistry has important implications for microwave remote sensing of
forested landscapes.
did not exceed 6…14 and 2 units,
respectively. The correlation between dielectric properties and water regime
and sap chemistry has important implications for microwave remote sensing of
forested landscapes.

Fig.1. Measured values of the imaginary part of the dielectric constant for different forest and plant constituents. [114]: 1 – new and old needles of the spruce and old needles of the fir; 2 – new needles of the fir; 3 – trunk xylem of the fir (in the longitudinal direction); 4 - trunk xylem of the spruce (in the longitudinal direction); [108]: 5 – corn leaves (mg = 0.68); [111]: 6 – Norway spruce trunk xylem; [117, 129]: 7 – aspen leaves; [128]: 8 – pine branches; [114]: 9 – branches xylem of the fir (in the longitudinal direction); [129]: 10 – trunk of balsam fir (mv = 0.17).
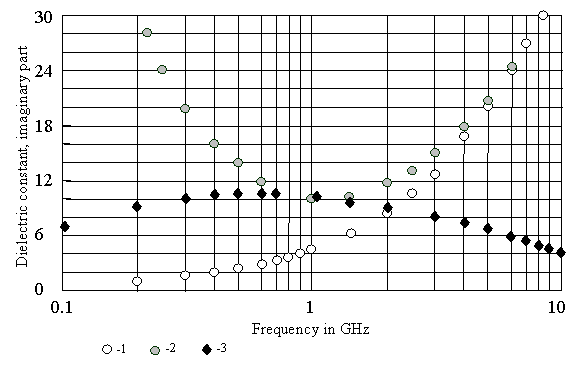
Fig.2. Frequency dependence of the imaginary part of the dielectric constant for free and bound water. 1 – free water (salinity S = 0 o/oo); 2 – free water (salinity S = 2 o/oo); 3 – bound water.
Similar values of spatial variations of the dielectric constant
were found in [114]. The measurements were conducted in the frequency range 1 –
10 GHz. The measurement method was based on an open ended coaxial probe
reflection technique with a rational function approximation model for the probe
tip aperture admittance. With this model, no calibration on reference liquids
is required and sufficiently accurate results for the dielectric constant (![]() ) and loss factor (
) and loss factor (![]() ) can be obtained.
Results were presented for branches, parts of trunks, and needles from different
tree heights. Values obtained with the probe oriented along different stem
directions of the trunk confirmed the anisotropic nature of wood. The
longitudinal complex permittivity was roughly 1.5 – 3 times higher than the
transverse component. Representative average values for trunks, branches, and
needles were given.
) can be obtained.
Results were presented for branches, parts of trunks, and needles from different
tree heights. Values obtained with the probe oriented along different stem
directions of the trunk confirmed the anisotropic nature of wood. The
longitudinal complex permittivity was roughly 1.5 – 3 times higher than the
transverse component. Representative average values for trunks, branches, and
needles were given.
From the standpoint of attenuation in vegetation it is interesting
to consider frequency dependence of ![]() . We plot some available data of
. We plot some available data of ![]() versus frequency
(Fig.1). Fig.2 shows the response of the imaginary part of the free and bound
water dielectric constant as a function of frequency [108, 111]. Analysis of
the data presented in Fig. 1, 2 shows the following.
versus frequency
(Fig.1). Fig.2 shows the response of the imaginary part of the free and bound
water dielectric constant as a function of frequency [108, 111]. Analysis of
the data presented in Fig. 1, 2 shows the following.
In the frequency
range 2…10 GHz (S, C, and X band) the loss factor of tree needles and leaves
amounts to 8…15. These values are higher than the highest values for corn
leaves. It can be explained by the other, than for corn leaves, apportionment
between free and bound water states in tree leaves tissue. The values of ![]() are in agreement with
data of the other researchers. Trunk xylem
are in agreement with
data of the other researchers. Trunk xylem ![]() changes in limits of 7…10; that is less
than
changes in limits of 7…10; that is less
than ![]() of
needles but higher than that of corn leaves. We have to note that other
researchers reported lower values of
of
needles but higher than that of corn leaves. We have to note that other
researchers reported lower values of ![]() for trunks. For example [129], at
frequency of 5 GHz measured data of
for trunks. For example [129], at
frequency of 5 GHz measured data of ![]() amounts to 1.96 – 5.97 for the old aspen,
to 1.2 – 6.34 for the spruce, to 0.93 – 6.13 for the old pine, and to 1.02 –
4.56 for the young pine. Low values of branches xylem
amounts to 1.96 – 5.97 for the old aspen,
to 1.2 – 6.34 for the spruce, to 0.93 – 6.13 for the old pine, and to 1.02 –
4.56 for the young pine. Low values of branches xylem ![]() in contrast to those of trunk
xylem, nevertheless, are in agreement with data of
in contrast to those of trunk
xylem, nevertheless, are in agreement with data of ![]() for young pine [129].
for young pine [129].
Frequency
dependence of ![]() in
the range 1…10 GHz are in good agreement with the dependence predicted by dual
dispersion model with appropriate composition of volume fractions of free water
in
the range 1…10 GHz are in good agreement with the dependence predicted by dual
dispersion model with appropriate composition of volume fractions of free water
![]() and bulk
vegetation – bound water mixture
and bulk
vegetation – bound water mixture ![]() . For green leaves
. For green leaves ![]() is large and contribution of
free water component is significant that leads to the increase of
is large and contribution of
free water component is significant that leads to the increase of ![]() with the increase of
frequency. Accurate choice of model parameters
with the increase of
frequency. Accurate choice of model parameters ![]() and
and ![]() could be done by fitting experimental data
like it was done in [108]. Our estimate shows that the measured values of
could be done by fitting experimental data
like it was done in [108]. Our estimate shows that the measured values of ![]() for leaves and the
observed slope of its frequency dependence can be provided by the model with
for leaves and the
observed slope of its frequency dependence can be provided by the model with ![]() = 0.2…0.3 and
= 0.2…0.3 and ![]() ~ 0.5. For example, we
plot the frequency dependence of
~ 0.5. For example, we
plot the frequency dependence of ![]() for
for ![]() = 0.3 and
= 0.3 and ![]() = 0.5 (S = 2o/oo). It is
shown in Fig.1 by asterisks. One can see that the model can well explain the
spectral behavior of
= 0.5 (S = 2o/oo). It is
shown in Fig.1 by asterisks. One can see that the model can well explain the
spectral behavior of ![]() .
Larger values of
.
Larger values of ![]() produce
greater slope of frequency dependence that is in a contradiction with
experiment. With low values of mv (see data for balsam fir in
Fig.1), the free water component is practically absent and frequency dependence
is similar to that of bound water mixture (Fig. 2).
produce
greater slope of frequency dependence that is in a contradiction with
experiment. With low values of mv (see data for balsam fir in
Fig.1), the free water component is practically absent and frequency dependence
is similar to that of bound water mixture (Fig. 2).
Maetzler’s
semi-empirical formula [115, 116] also gives good agreement with experimental
data. We plot the calculated data in Fig.1 by black points for ![]() = 0.4 and S = 2o/oo.
It should be noted that smaller values of
= 0.4 and S = 2o/oo.
It should be noted that smaller values of ![]() would produce greater slope of frequency
dependence that disagrees with experiment.
would produce greater slope of frequency
dependence that disagrees with experiment.
Unfortunately, we
couldn’t find data on dielectric properties of tree leaves and branches in the
frequency range 0.1 – 1 GHz (data for corn leaves are presented in [108, 117]).
Probably the open-ended coaxial probe reflection technique meets some
difficulties in this frequency domain [114] and should be further developed or
another technique should be suggested. There are also very few data for trunks
in this band. We think that extensive measurements of ![]() in this frequency range with
continuous change of frequency (like it was done in [114] in the range 1.9 –
9.1 GHz) would be extremely useful to understand the frequency dependence of
attenuation by vegetation and of emission and backscattering from vegetated
terrain.
in this frequency range with
continuous change of frequency (like it was done in [114] in the range 1.9 –
9.1 GHz) would be extremely useful to understand the frequency dependence of
attenuation by vegetation and of emission and backscattering from vegetated
terrain.
5. EM waves propagation through a vegetation layer. Relation between electromagnetic and biometric vegetation parameters.
To calculate radar
return (or emissivity) from vegetation canopies the vector radiative transfer
equation is used [96]. It is of the following form: For ![]()
 (43)
(43)
where ![]() is a 4´1 column vector denoting the modified
Stokes parameters in direction
is a 4´1 column vector denoting the modified
Stokes parameters in direction ![]() ,
, ![]() is the 4´4 phase matrix denoting scattering
from direction
is the 4´4 phase matrix denoting scattering
from direction ![]() into direction
into direction ![]() , and
, and ![]() is the extinction matrix which
can be expressed in terms of the forward scattering amplitudes (see Section 3.1).
For the case of thermal emission the right side of the equation is added by the
term
is the extinction matrix which
can be expressed in terms of the forward scattering amplitudes (see Section 3.1).
For the case of thermal emission the right side of the equation is added by the
term ![]() where
where ![]() is the absorption matrix and T is the physical
temperature of the canopy.
is the absorption matrix and T is the physical
temperature of the canopy.
The relation between
the components of ![]() , particularly, the extinction
coefficient g for given polarization (or the optical depth
, particularly, the extinction
coefficient g for given polarization (or the optical depth ![]() ) and biometric
parameters is established by expressions (26) – (30). The extinction cross
sections are calculated for simple geometric elements (ellipsoid, cylinder, and
disc) (see Section 3.2.1) which are characterized by their dimensions and
dielectric constant (see Section 4).
) and biometric
parameters is established by expressions (26) – (30). The extinction cross
sections are calculated for simple geometric elements (ellipsoid, cylinder, and
disc) (see Section 3.2.1) which are characterized by their dimensions and
dielectric constant (see Section 4).
For the simplest case of small chaotic ellipsoids it was obtained [3, 48] using (33) and (34)
![]() (44)
(44)
where u = 1 for small needles and u = 2 for small discs (see the nomenclature in Section 1.1). For other cases the semi-empirical equations is used [48, 2]
![]() (45)
(45)
where A is the coefficient
(form factor) related to the plant structure, f is the frequency. Taking into
account that ![]() in
the microwave band weakly depends on the frequency (see Fig.1) and
in
the microwave band weakly depends on the frequency (see Fig.1) and ![]() ~ 10 the simple
equation could be obtained for attenuation by crops and foliage in the
frequency range 1 – 10 GHz [3, 28, 29, 130]
~ 10 the simple
equation could be obtained for attenuation by crops and foliage in the
frequency range 1 – 10 GHz [3, 28, 29, 130]
![]() (46)
(46)
where a is the attenuation in dB,
U = 2.5…5 depending on the vegetation type, l is the wavelength in cm (l[cm] = ![]() ), W is the
vegetation water content in kg per square meter. More complicated equations are
given in [74].
), W is the
vegetation water content in kg per square meter. More complicated equations are
given in [74].
The equations given above are very simple and can provide only rough estimates of attenuation by vegetation canopies. Nevertheless, these expressions are rather useful since they help someone to understand what the attenuation in vegetation depends on.
To obtain more accurate estimates of attenuation numerical solution of the transfer equation is used [1, 17 – 19]. The scattering amplitudes of dielectric needles, discs, and cylinders are computed on the base of generalized Rayleigh-Gans approach or other developed approaches for dimensions and dielectric constant of scatterers obtained from in-situ measurements (see Table 2 and 3). Computed data of backscattering coefficients are in good agreement with experimental data [1]. Unfortunately, when a numerical solution of transfer equation is used it is rather difficult to separate the influence of the change of model parameters (dimension of scatterers, their number density and moisture content, etc) on the value of attenuation or backscattering coefficient. In other words, it is not clear enough as to what biometric parameters determine the attenuation by a canopy and how strong they influence the attenuation.
Besides, applying the numerical solution, a researcher should remember the following.
i. Vegetation elements are substituted in the model by simple forms like circular discs and circular cylinders of finite length. However, even for these bodies the rigorous solution of the diffraction problem is not known and approximate models are used. The extinction coefficient is calculated as the sum of extinction cross sections of elements occupied a unit volume (30). That does not take into account the effects of mutual screening and correlation of scatterers [3, 74]. As a result, the error of the model can be significant.
ii. Because a vegetation canopy is an inhomogeneous medium, its coherent attenuation should be treated as a random value [8]. Calculating extinction with given dimensions, angular distributions, and number densities of scatterers we should understand that we obtain the mean value of extinction and the sampling values can change in wide limits for the given canopy. For example, variations of attenuation for corn canopy amounts to 50 % and more within the test site [8]. It shows that it is interesting to know the relative level of attenuation at different frequencies rather than absolute values of attenuation.
Theoretical models are extremely important and should play a vital role in the research process since they are indispensable for conducting sensitivity analyses and for pointing the directions of future research. But, in our opinion, because any model is based on certain assumptions, modeling process can only indicate the factors determining, for instance, attenuation by vegetation. Parameters of the model should be found by regression analysis of experimental data. For example, for a part of the frequency band considered the extinction coefficient could be found out in the form [130]
![]() (47)
(47)
where A is the form factor determining by vegetation type, b is the coefficient depending on the vegetation moisture content, f is the frequency, and w is vegetation water content per unit volume. Other forms of the regression models can be also suggested.
The angular dependences of attenuation by stands described in Table 1 and 2 are presented in [1] for different frequency bands. Attenuation is given as the percent of radar beam power lost (scattered and absorbed) while traveling through the canopy along the direction of propagation to the forest floor. We recalculated these data to the attenuation in decibels. These data for incident angle of 30° are presented in Table 5.
Table 5. Attenuation by the stands from Table 2 and 3.
|
Stand |
Attenuation in dB (H polarization) |
|||
|
P – band |
L – band |
C – band |
X – band |
|
|
Aspen leaf on |
2.2 |
3.5 |
16 |
> 16 |
|
Hemlock leaf on |
0.7 |
2.4 |
12.5 |
>16 |
|
Maple/beech |
4 |
11 |
16 |
|
|
Red/white pine |
1.7 |
5.5 |
13 |
|
One can see that the computed attenuation values differ from each other by several times for the stands. Strong frequency dependence of attenuation is present.
Polarization signatures of attenuation arise when an oriented component (stalks, trunks) is present in the vegetation canopy [6-9, 17-19, 29, 38, 58, 73, 74, 79, 83, 97, 100, 103]. The difference in attenuation of vertically and horizontally polarized waves can be large and is used in retrieving algorithms [28, 29, and 38].
Shutko
III. EXPERIMENTAL STUDIES OF EM WAVES ATTENUATION IN VEGETATION CANOPIES.
1. The methods of measurements.
Measurements of attenuation by vegetation were conducted under laboratory conditions, under ground-based field conditions, and from aircrafts.
Laboratory experiments have the advantage that parameters of investigated objects can be changed and controlled. They allow examining the influence of individual parameters on the EM propagation characteristics of the medium.
Ground-based field measurements produced the largest amount of information on propagation properties of vegetation canopies. The natural conditions provide the possibility to obtain data during the whole period of canopy growth and to compare them with ground truth data.
Airborne sensors provide a possibility to gather quickly a large data set for different types of vegetation under various states and conditions.
Methods which were used to measure the attenuation can be divided into active and passive ones. In active methods, the attenuation over the path between transmitting and receiving antennas is measured. Airborne radar studies used corner reflectors and active calibrators placed on the ground at different locations within a canopy. Several typical configurations of active measurements are presented in Fig.3.
Configuration Fig.3 A) was used in [7, 8, 58, and 109] to measure attenuation in different crops such as wheat, corn, soybeans, etc. The transmitters were placed on a truck-mounted platform and the receivers were
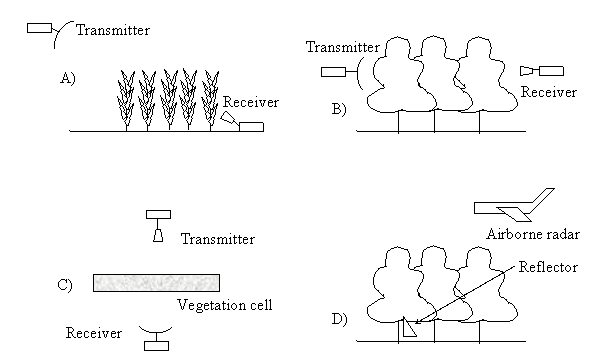
Fig.3. Typical configurations of active measurements of attenuation.
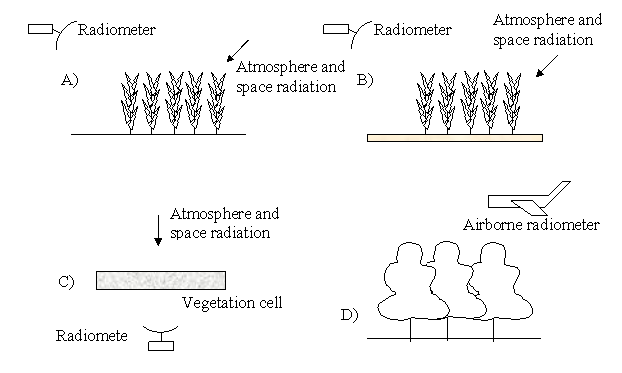
Fig.4. Typical configurations of passive measurements of attenuation.
placed underneath the canopy. Measurements were conducted at different frequencies, polarizations, and incidence angles. Besides, measurements of the phase difference between horizontally polarized and vertically polarized simultaneously transmitted waves were presented in [8]. Calibration was provided by cutting and removing the plants to establish a free-space reference signal.
Configuration Fig.3 B) with different height of antennas above the ground is usually used for investigation of electromagnetic waves propagation in forest environment [131, 139-142, 163].
Configuration Fig.3 C) was used in laboratory measurements of attenuation by forest litter [112] and forest fragments [103]. A vector network analyzer measured the power and phase of the signal passing through the cell [112].
Attenuation constant of a layer was determined by comparing measurements of litter with that of the empty cell. In work [103], vegetation samples were placed on a Styrofoam frame, in one row or several rows with different spacing. Measurements were performed with vegetative targets and the transmitted power was recorded. After removing the targets the reference power was then recorded to find the attenuation.
Configuration Fig.3 D) is used in airborne and space borne radar studies of attenuation and backscattering [132-138, 155-158, 160, 161, 164]. Attenuation is determined by comparing signals from reflectors placed beneath the canopy and placed on the open ground.
Passive methods use the measurements of thermal emission from the investigated object in the presence of atmosphere and space emission as the background. Typical configurations used in passive (radiometric) measurements of attenuation are shown in Fig.4.
Configuration Fig 4. A) was proposed in [30, 6] for the field measurements of attenuation by corn and soybeans. The zero-order solution of the transfer equation for the emission from vegetated soil was reduced to
![]() (48)
(48)
where T0
is the vegetation and soil physical temperature, Rs is the
reflectivity of the soil surface (![]() ), and Tsky is the down
welling sky (atmosphere and space) brightness temperature. The simplified
equation was used to determine the reflectivity r and the transmissivity
q by measuring the brightness temperature Tb for a)
bare soil, b) canopy over soil, c) bare absorbing material with an emissivity
close to unit, and d) canopy over the absorbing material. To increase the
accuracy of measurements the soil was covered by screens which were wire meshes
with an inter wire spacing of 1.6 mm and wire thickness of 0.3 mm. The
brightness temperature was measured by a dual-frequency 2.7 and 5.1 GHz),
dual-polarization radiometer mounted atop a truck-mounted boom. It was shown
that the canopy is highly anisotropic, the emission exhibits a strong
dependence on polarization and look direction, and the reflectivity is
typically less than 0.1.
), and Tsky is the down
welling sky (atmosphere and space) brightness temperature. The simplified
equation was used to determine the reflectivity r and the transmissivity
q by measuring the brightness temperature Tb for a)
bare soil, b) canopy over soil, c) bare absorbing material with an emissivity
close to unit, and d) canopy over the absorbing material. To increase the
accuracy of measurements the soil was covered by screens which were wire meshes
with an inter wire spacing of 1.6 mm and wire thickness of 0.3 mm. The
brightness temperature was measured by a dual-frequency 2.7 and 5.1 GHz),
dual-polarization radiometer mounted atop a truck-mounted boom. It was shown
that the canopy is highly anisotropic, the emission exhibits a strong
dependence on polarization and look direction, and the reflectivity is
typically less than 0.1.
The technique described ensures good accuracy but it is very cumbersome. Field measurements of the transmissivity were conducted with microwave radiometers mounted on a truck [5, 11, and 134] and on a car [133]. The transmissivity was estimated by the relation that one can easy obtain from (1)
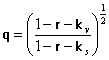 (49)
(49)
where ![]() and
and ![]() are the emissivity of vegetated
and bare soil, respectively, with the same moisture content (and the
reflectivity) within a site.
are the emissivity of vegetated
and bare soil, respectively, with the same moisture content (and the
reflectivity) within a site.
The technique proposed in [30, 6] for field measurements can be easily performed under the laboratory conditions [100, 77, 145-147] (configuration Fig. 4 B)). The fresh-cut plants were placed on the reflector located in the far zone of the antenna of the radiometer. As the reflector, a “blackbody” and a metal plate were used. The transmissivity of the vegetation layer was estimated from the expression
![]() (50)
(50)
where ![]() is the brightness temperature
contrast between the bare blackbody and the bare metal plate and
is the brightness temperature
contrast between the bare blackbody and the bare metal plate and ![]() is the same contrast
but when the reflectors are covered by vegetation.
is the same contrast
but when the reflectors are covered by vegetation.
Configuration Fig. 4 C) was used in [74] to measure the transmissivity of a vegetation layer and in [148, 68] for field measurements of the transmissivity of trees. Attenuation values were estimated by comparing measurements of the brightness temperature with vegetation and without vegetation.
Configuration Fig. 4 D) is used for measurements of attenuation with the help of airborne radiometers [48, 150, and 151].
2. The results of measurements and their comparison with calculating data.
Agricultural vegetation.
Data of measurements of attenuation by crops in the microwave band for different polarizations and look directions are presented in papers [2 - 9, 11, 26-32, 34-36, 40, 43, 48, 49, 53, 54, 58, 69, 71, 74, 81, 100, 109, 130, 143-145]. Analysis of the data shows the following [130].
The dependence of attenuation on the vegetation water content can be approximated by a linear function, i.e. expressions (44) – (46) give a satisfactory estimate for this dependence. Nonlinear dependence of the attenuation on the water content was reported in [3, 5, 40, and 74] and can be explained by mutual screening of vegetation elements [3] or by the temporal change of vegetation water status [40, 74].
Fig.5. Characteristic values of attenuation by different crops. 1 – corn, sunflower; 2 – pea, alfalfa; 3 – grains (wheat, barley, oat, etc); 4 – soybeans, cotton.

Fig.6. Experimental data on attenuation by different forests. 1, 2, 3, 4 – [64]; 5 – calculated data from [83]; 6 – [151]; 7, 8 – [154]; 9 – [135]; 10 – [134, 152]; 11 – [153].
The generalized
frequency dependence of attenuation is presented in Fig. 5 [130]. Data in Fig.
5 relate to the mature state of crops and represent the maximum level of
attenuation. In the microwave band, the attenuation by crops is proportional to
the frequency in (![]() )
power (
)
power (![]() ) where
d
= 0…0.2 depending on the crop and vegetation moisture content.
) where
d
= 0…0.2 depending on the crop and vegetation moisture content.
In the microwave band, a
rough estimate of attenuation can be obtained from expression (46) ![]() . The calculated
dependence of attenuation for U = 3 and W = 4 kg/m2 is
presented in Fig.5 by the dashed line. More accurate estimate of attenuation
can be obtained from the models taking into account the vegetation structure
and dimensions, orientation, and dielectric properties of leaves and stalks
(Sections 4 and 5). Numerical calculation of attenuation with use of a computer
is required in this case [8].
. The calculated
dependence of attenuation for U = 3 and W = 4 kg/m2 is
presented in Fig.5 by the dashed line. More accurate estimate of attenuation
can be obtained from the models taking into account the vegetation structure
and dimensions, orientation, and dielectric properties of leaves and stalks
(Sections 4 and 5). Numerical calculation of attenuation with use of a computer
is required in this case [8].
We could not find experimental data on attenuation by crops in the frequency range 100…1000 MHz. In this band, the salinity of free water contained in vegetation material (or conductivity of plant elements) could be a major factor determining the spectral dependence of attenuation. This factor is not yet sufficiently studied. Measurements and modeling of attenuation in the frequency range 100…1000 MHz and of direct current conductivity of plant elements could be a subject of future research.
Forest vegetation.
Experimental data of the extinction coefficient for different types of forests (rain, coniferous, deciduous) are presented in Fig. 6. We recalculated data on penetration depths found in [1, 83, 134, 135, 151 -153] in the values of attenuation in dB per meter; some data are reported in [64, 154].
Available data of the attenuation by forest canopies are very limited and it is rather difficult to make certain conclusions about the attenuation and its spectral dependence. Nevertheless, the data presented can give someone an idea about observed values of the attenuation and their dependence on the frequency. Analysis of the data shows the following.
There is not a big difference in attenuation values for different types of forests in 100…1000 MHz frequency range. For higher frequencies the values of extinction coefficient at a given frequency reported by different authors differ from each other by several (2…5) times.
The data in Fig. 6 show the general trend of frequency dependence of extinction. In the frequency range 100…1000 MHz this dependence can be approximated by a linear dependence [130]
![]() b = 0.8
(51)
b = 0.8
(51)
where ![]() is the attenuation in dB per
meter, c = 8×10-4 is the regression coefficient, and f
is the frequency in MHz. This dependence is shown in Fig. 6 by the dashed line.
In the frequency range 1000…10000 MHz a greater slope of frequency dependence
is observed.
is the attenuation in dB per
meter, c = 8×10-4 is the regression coefficient, and f
is the frequency in MHz. This dependence is shown in Fig. 6 by the dashed line.
In the frequency range 1000…10000 MHz a greater slope of frequency dependence
is observed.
The values of attenuation (5 in Fig.6) calculated by the model [83] are in agreement with experimental data reported by other researchers. However, the slope of model frequency dependence does not coincide with the general trend of frequency dependence for data presented in Fig.6.
The total extinction in a forest media at frequencies below 1000 MHz is mainly determined by extinction by branches and trunks [1, 64]. The last is not completely studied. A further development of attenuation models requires spectral measurements of attenuation in the wide band and measurements of dielectric constant and conductivity of branches and leaves.
IV. CONCLUSIONS.
An analytical overview conducted in the paper allows us to make the following concluding remarks.
Due to the efforts of many researchers and research groups the basic questions of EM propagation and attenuation in vegetation canopies are clarified. Appropriate models are developed to describe the extinction of EM waves by plant elements and by vegetation volume as a whole. Theoretical and empirical models are available to calculate the dielectric constant of vegetation material in the microwave band. Experimental data of dielectric constant and of attenuation are well fitted by the models.
Nevertheless, several problems remain unsolved that enables one to point the directions of future research areas. In our opinion, these areas could be:
i. Extensive measurements of dielectric permittivity of plant elements in 100…1000 MHz frequency range and of the direct current conductivity of different plant elements;
ii. Extensive measurements of EM attenuation spectra by vegetation canopies under laboratory and field conditions;
iii. Verification of the known models and developing, if it is necessary, new ones to fit spectral data of attenuation.
The designated research areas are planned to be a subject of our further work.
REFERENCES
1. D.G. Leckie and K.J. Ranson, “Forestry applications using imaging radar,” in Principles and Applications of Imaging Radar, Edited by F.M. Henderson and A.J. Lewis, pp. 435-509, Wiley, 1998.
2. A. Chanzy and J.-P. Wigneron, “Microwave emission from soil and vegetation,” In Radiative Transfer Models for Microwave Radiometry, Edited by Ch. Maetzler, Bern, Switzerland, pp. 89-102, Feb. 2000.
3. A.A. Chukhlantsev, “Microwave emission and scattering from vegetation canopies,” Journal of Electromagnetic Waves and Applications, Vol. 6, No. 8, pp. 1043 – 1068, 1992.
4. A.E. Basharinov, E.N. Zotova, M.I. Naumov, and A.A. Chuklantsev, “Radiation characteristics of vegetation in the microwave band,” Radiotekhnika, Vol. 34, No. 5, pp. 16-24, 1979 (in Russian).
5. P. Pampaloni and S. Paloscia, “Microwave emission and plant water content: a comparison between field measurements and theory,” IEEE Trans. Geosci. Remote Sensing, Vol. 24, pp. 900-905, Nov. 1986.
6. D.V. Brunfeldt and F.T. Ulaby, “Microwave emission from row crops,” IEEE Trans. Geosci. Remote Sensing, Vol. 24, pp. 353-359, May 1986.
7. C.T. Allen and F.T. Ulaby, “Modelling the polarization dependence of the attenuation in vegetation canopies,” Proc. of IGARSS’84, Strasbourg, 27-30 August, 1984, pp.119-124.
8. F.T. Ulaby, A. Tavakoli, and T.B.A. Senior, “Microwave propagation constant for a vegetation canopy with vertical stalks,” IEEE Trans. Geosci. Remote Sensing, Vol. 25, pp. 714-725, Nov. 1987.
9. Ch. Maetzler, “Seasonal evolution of microwave radiation from an oat field,” Remote Sens. Environ. Vol. 31, pp. 161 173, 1990.
10. E.P.T. Attema and F.T. Ulaby, “Vegetation modeled as a water cloud,” Radio Science, Vol. 13, No. 2, pp. 357-364, March-April 1978.
11. A.A. Chukhlantsev, S.P. Golovachev, and A.M. Shutko, “Experimental study of vegetable canopy microwave emission,” Adv. Space Res. Vol.9, No. 1, pp. (1)317-(1)321, 1989.
12. R.A. Orlov and B.D. Torgashin. Modeling radar return from the Earth’s surface. Leningrad, 1978. (in Russian)
13. V.V. Smirnov. Organic mass in some forest phytocenosis of Europe part of USSR. Moscow, Nauka, 1971. (inRussian)
14. P.U. Richards. Tropical rain forest. Moscow, 1961. (in Russian)
15. T. Satoo, “Primary production relations of coniferous forests in Japan,” In Productivity of Forest Ecosystems. Proceedings of the Brussels Symposium 27-31 October 1969. Edited by P. Duvigneaud, UNESCO, Paris, 1971, pp. 191-205.
16. T. Kira and H. Ogava, “Assessment of primary production in tropical and equatorial forests,” In Productivity of Forest Ecosystems. Proceedings of the Brussels Symposium 27-31 October 1969. Edited by P. Duvigneaud, UNESCO, Paris, 1971, pp. 309-321.
17. G. Sun, D.S. Simonett, and A.H. Strahler, “A radar backscatter model for discontinuous coniferous forests,” IEEE Trans. Geosci. Remote Sensing, Vol. 29, pp. 639-648, 1991.
18. Y. Wang, J. Day, and G. Sun, “Santa Barbara microwave backscattering model for woodlands,” Int. J. Remote Sensing, Vol. 14, No. 8, pp. 1477-1493, 1993.
19. F.T. Ulaby, K. Sarabandy, K. McDonald, M. Whitt, and M.C. Dobson, “Michigan microwave canopy scattering model,” Int. J. Remote Sensing, Vol. 11, No. 7, pp. 1223-1253, 1990.
20. P. Melon, J.-M. Martinez, T. Le Toan, L.M.H. Ulander, and A. Beaudoin, “On the retrieving of forest stem volume from VHF SAR data: observation and modeling,” IEEE Trans. Geosci. Remote Sensing, Vol. 39, pp. 2364-2372, Nov. 2001.
21. T. Le Toan, A. Beaudoin, J. Riom, and D. Guyon, “Relating forest biomass to SAR data,” IEEE Trans. Geosci. Remote Sensing, Vol. 30, pp. 403-411, Mar. 1992.
22.
M.C. Dobson, F.T. Ulaby,
T. Le Toan, A. Beaudoin, E.S. Kasischke, and
N.L. Christensen Jr., “Dependence of radar backscatter on coniferous forest
biomass,” IEEE Trans. Geosci. Remote Sensing, Vol. 30, pp. 412-415, Mar.
1992.
23. M.L. Imhoff, “A theoretical analysis of the effect of forest structure on Synthetic Aperture Radar backscatter and the remote sensing of biomass,” IEEE Trans. Geosci. Remote Sensing, Vol. 33, pp. 341-352, Mar. 1995.
24. Y.-A. Liou, S.-F. Liu, and W.-J. Wang, “Retrieving soil moisture from simulated brightness temperatures by a neural network,” IEEE Trans. Geosci. Remote Sensing, Vol. 39, pp. 1662-1672, Aug. 2001.
25. S.-F. Liu, Y.-A. Liou, W.-J. Wang, J.-P. Wigneron, and J.-B. Lee, “Retrieval of crop biomass and soil moisture from measured 1.4 and 10.65 GHz brightness temperature,” IEEE Trans. Geosci. Remote Sensing, Vol. 40, pp. 1260-1268, June 2002.
26. J.R. Wang, R.W. Newton, and J.W. Rouse Jr., “Passive microwave remote sensing of soil moisture,” IEEE Trans. Geosci. Remote Sensing, Vol. 18, pp. 296-302, Apr. 1980.
27. T.J. Jackson and T.J. Schmugge, “Passive microwave remote sensing system for soil moisture: Some supporting research,” IEEE Trans. Geosci. Remote Sensing, Vol. 27, pp. 225-235, Jan. 1989.
28. A.A. Chukhlantsev and A.M. Shutko, “Application of microwave radiometry for determining biometric parameters of vegetation canopies,” Issledovanie Zemli iz Kosmosa (Research of the Earth from Space), No. 5, pp. 42-48, 1987 (in Russian).
29. A.A. Chukhlantsev and A.M. Shutko, “Microwave radiometry of the Earth’s surface: effect of vegetation,” Issledovanie Zemli iz Kosmosa (Research of the Earth from Space), No. 2, pp. 67-72, 1988 (in Russian).
30. D.R. Brunfeld and F.T. Ulaby, “Measured microwave emission and scattering in vegetation canopy,” IEEE Trans. Geosci. Remote Sensing, Vol. 22, pp. 520-524, Nov. 1984.
31. H.-H. Burke and T.J. Schmugge, “Effect of varying soil moisture contents and vegetation canopies on microwave emission,” IEEE Trans. Geosci. Remote Sensing, Vol. 20, pp. 268-274, July. 1982.
32. F.T. Ulaby, M. Razani, and M.C. Dobson, “Effect of vegetation cover on the microwave radiometric sensitivity to soil moisture,” IEEE Trans. Geosci. Remote Sensing, Vol. 21, pp. 51-61, Jan. 1982.
33. E.G. Njoku and Li Li, “Retrieval of land surface parameters using passive microwave measurements at 6-18 GHz,” IEEE Trans. Geosci. Remote Sensing, Vol. 37, pp. 79-93, Jan. 1999.
34. T.J. Jackson, “Soil moisture estimation using special satellite microwave/imager satellite data over a grassland region,” Water Resources Res., Vol. 33, pp. 1475-1484, 1997.
35. J.P. Wigneron, Y.H. Kerr, A. Chanzy, and Y.Q. Jin, “Inversion of surface parameters from passive microwave measurements over a soybean field,” Remote Sens. Environ., Vol. 46, pp. 61-72, 1993.
36. J.P. Wigneron, A. Chanzy, J.C. Calvet, and N. Brugier, “A simple algorithm to retrieve soil moisture and vegetation biomass using passive microwave measurements over crop fields,” Remote Sens. Environ., Vol. 51, pp. 331-341, 1995.
37. J.P. Wigneron, P. Waldteufel, A. Chanzy, J.C. Calvet, and Y. Kerr, “Two dimensional microwave interferometer retrieval capabilities over land surface (SMOS mission),” Remote Sens. Environ., Vol. 73, pp. 270-282, 2000.
38. M. Owe, R. de Jeu, and J. Walker, “A methodology for surface soil moisture and vegetation optical depth retrieval using the microwave polarization difference index,” IEEE Trans. Geosci. Remote Sensing, Vol. 39, pp. 1643-1654, Aug. 2001.
39. T. Castel, A. Beaudoin, N. Floury. T. Le Toan, Y. Caraglio, and J.-F. Barczi, “Deriving Forest canopy parameters for backscatter models using the AMAP architectural plant model,” IEEE Trans. Geosci. Remote Sensing, Vol. 39, pp. 571-583, Mar. 2001.
40. R.D. De Roo, Y. Du, F.T. Ulaby, and M.C. Dobson, “A semi-empirical backscattering model at L-band and C-band for a soybean canopy with soil moisture inversion,” IEEE Trans. Geosci. Remote Sensing, Vol. 39, pp. 864-872, Apr. 2001.
41. H.J. Eom and A.K. Fung, “A scatter model for vegetation up to Ku-band,” Remote Sens. Environ., Vol. 15, pp. 185-200, 1984.
42. R.H. Lang and J.S. Sidhu, “Electromagnetic backscattering from a layer of vegetation: a discrete approach,” IEEE Trans. Geosci. Remote Sensing, Vol. 21, pp. 62-71, Jan. 1983.
43. P. Ferrazoli, L. Guerriero, S. Paloscia, P. Pampaloni, and D. Solimini, “Modelling polarization properties of emission from soil covered with vegetation,” IEEE Trans. Geosci. Remote Sensing, Vol. 30, pp. 157-165, Jan. 1992.
44. S.L. Chuang, J.A. Kong, and L. Tsang, “Radiative transfer theory for passive microwave remote sensing of a two layer random medium with cylindrical structure,” J. Appl. Phys., Vol. 51, pp. 5588-5593, 1982.
45. P. Ferrazoli and L. Guerriero, “Passive microwave remote sensing of forest: a model investigation,” IEEE Trans. Geosci. Remote Sensing, Vol. 34, pp. 433-443, May 1996.
46. S.I. Vinokurova, M.T. Smirnov, and A.A. Chukhlantsev, “Microwave radiative model for scattering layer above a rough surface,” Izvestia VUZ’ov, Radiofizika (Engl. Transl. Radiophys, Quantum Electron.), No. 4, pp.472-476, 1991 (in Russian).
47. A.K. Fung and H.J. Eom, “A comparison between active and passive sensing of soil moisture from vegetated terrain,” IEEE Trans. Geosci. Remote Sensing, Vol. 23, pp. 768-775, 1985.
48. K.P. Kirdiashev, A.A. Chukhlantsev, and A.M. Shutko, “Microwave radiation of the Earth’s surface in the presence of vegetation cover,” Radio Eng. Electron. Phys. Engl. Transl., Vol. 24, pp. 256-264, 1979.
49. T. Mo, B.J. Choudhury, T.J. Schmugge, J.R. Wang, and T.J. Jackson, “A model for microwave emission from vegetation-covered fields,” J. Geophys. Res., Vol. 87, pp. 11229-11237, 1982.
50. A.A. Chukhlantsev and S.I. Vinokurova, “On application of radar equipment for remote sensing of vegetation and soil,” Issledovanie Zemli iz Kosmosa (Research of the Earth from Space), No. 4, pp. 21-26, 1991 (in Russian).
51. A.A. Chukhlantsev, “A possible model approach to vegetation cover classification from radar sounding data,” Issledovanie Zemli iz Kosmosa (Research of the Earth from Space), No. 4, pp. 84-90, 1989 (in Russian).
52. F.T. Ulaby and T.F. Bush, “Monitoring wheat growth with radar,” Photogrammetric Engineering and Remote Sensing, Vol. 42, No. 4, pp.557-568, Apr. 1976.
53. P. Pampaloni and S. Paloscia, “Experimental relationships between microwave emission and vegetation features,” Int. J. Remote Sensing, Vol. 6, pp. 315-323, 1985.
54. S. Paloscia and P. Pampaloni, “Microwave polarization index for monitoring vegetation growth,” IEEE Trans. Geosci. Remote Sensing, Vol. 26, pp. 617-621, Sept. 1988.
55. B.J. Choudhury, M. Owe, S.N. Goward, R.E. Golus, J.P. Ormsby, A.T.C. Chang, and J.R. Wang, “Quantifying spatial and temporal variabilities of microwave brightness temperature over the U.S. southern great plains,” Int. J. Remote Sensing, Vol. 8, pp. 177-191, 1987.
56. W.C.Y. Lee, Mobile Communication Engineering, McGraw-Hill Book Company.
57. Yu.A. Ryzhov and V.V. Tamoikin, “Radiation and propagation of electromagnetic waves in randomly inhomogeneous media,” Radiophys. Quantum. Electron., Vol. 13, pp. 273-300, 1970.
58. F.T. Ulaby and E.A. Wilson, “Microwave attenuation properties of vegetation canopies,” IEEE Trans. Geosci. Remote Sensing, Vol. 23, pp. 746-753, Sept. 1985.
59. A.K. Fung and H.S. Fung, “Application of first order renormalization method to scattering from a vegetation-like half-space,” IEEE Trans. Geosci. Remote Sensing, Vol. 15, pp. 189-195, 1977.
60. A.K. Fung and F.T. Ulaby, “A scatter model for leafy vegetation,” IEEE Trans. Geosci. Remote Sensing, Vol. 16, pp. 281-285, 1978.
61. A.K. Fung, “Scattering from a vegetation layer,” IEEE Trans. Geosci. Remote Sensing, Vol. 17, pp. 1-6, 1979.
62. L. Tsang and J.A. Kong, “Application of strong fluctuation random medium theory to scattering from vegetation-like half space,” IEEE Trans. Geosci. Remote Sensing, Vol. 19, pp. 62-69, 1981.
63. A.A. Chukhlantsev, “On effective dielectric permittivity of vegetation in the microwave band,” Radiotekhnika i Elektronika (Eng. Transl. as Radio Eng. Electron. Phys.), Vol. 33, pp. 2310-2319, 1988 (In Russian).
64. D.T. Tamasanis, “Application of volumetric multiple scattering approximations to foliage media,” Radio Science, Vol. 27, No. 6, pp. 797-812, 1992.
65. L.-J. Du and W.H. Peake, “Rayleigh scattering from leaves,” Proc. of IEEE, Vo. 57, No. 6, p. 1227, 1969.
66. B.A. Redkin, V.V. Klochko, and G.G. Ocheret, “Theoretical and experimental study of reflection coefficient of vegetation canopies at small sliding angles,” Izvestia VUZ’ov, Radiofizika (Engl. Transl. Radiophys, Quantum Electron.), Vol. 16, No. 8, p. 1178, 1973 (in Russian).
67. B.A. Redkin and V.V. Klochko, “Calculation of averaged of dielectric permittivity tensor for vegetation media,” Radiotekhnika i Elektronika (Eng. Transl. as Radio Eng. Electron. Phys.), Vol. 22, No. 8, pp. 1596-1599, 1977 (In Russian).
68. A.A. Milshin and A.G. Grankov, “Some experimental results of microwave emission of forests in L-band,” Issledovanie Zemli iz Kosmosa (Research of the Earth from Space), No. 3, pp. 50-57, 2000 (in Russian).
69.
Y.H. Kerr and J.P. Wigneron,
“Vegetation model and observations. A review,” ESA/NASA International
Workshop. VSP, Eds.: B.J. Choudhury, J.H. Kerr, E.G. Njoku, and
P. Pampaloni, 1994, pp.317-344.
70. R.J. Papa and D.T. Tamasanis, “A model for bistatic scattering of electromagnetic waves from foliage covered rough terrain,” NATO Workshop: Target and Cluster Scattering and their Effects on Military Radar Performance, 6 - 10 May 1991, pp. 4-1 – 4-7.
71. T.J. Schmugge and T.J. Jackson, “A dielectric model of the vegetation effects on the microwave emission from soils,” IEEE Trans. Geosci. Remote Sensing, Vol. 30, pp. 757-760, 1992.
72. L.F. Borodin, K.P. Kirdiashev, Yu.P. Stakankin, and A.A. Chukhlantsev, “On the application of microwave radiometry to forest fire surveys,” Radiotekhnika i Elektronika (Eng. Transl. as Radio Eng. Electron. Phys.), Vol. 21, No. 8, pp. 1945-1950, 1976 (In Russian).
73. A.A. Chukhlantsev, “On modeling vegetation as a collection of scatterers,” Radiotekhnika i Elektronika (Eng. Transl. as Radio Eng. Electron. Phys.), Vol. 34, pp. 24-244, 1989 (In Russian).
74. A.A. Chukhlantsev and S.P. Golovachev, “Microwave attenuation in a vegetation canopy,” Radiotekhnika i Elektronika (Eng. Transl. as Radio Eng. Electron. Phys.), Vol. 34, pp. 2269-2278, 1989 (In Russian).
75. W.H. Peake, “Interaction of electromagnetic waves with some natural surfaces,” IRE Trans. Antennas. Propagat., Vol. AP-7, s325-s329, 1959.
76. R.H. Lang, “Electromagnetic backscattering from a sparse distribution of lossy dielectric scatterers,” Radio Science, Vol. 16, pp. 15-30, 1981.
77. M.A. Karam and A.K. Fung, “Scattering from randomly oriented circular discs with application to vegetation,” Radio Science, Vol. 18, pp. 557-565, 1983.
78. M.A. Karam and A.K. Fung, “Electromagnetic scattering from a layer of finite lenth, randomly oriented, dielectric, circular cylinders over a rough interface with application to vegetation,” Int. J. Remote Sensing, Vol. 9, pp. 1109-1134, 1988.
79. N.S. Chauhan and R.H. Lang, “Polarization utilization in the microwave inversion of leaf angle distribution,” IEEE Trans. Geosci. Remote Sensing, Vol. 27, pp. 395-402, 1989.
80. M.A. Karam and A.K. Fung, “Leaf-shape effects in electromagnetic wave scattering from vegetation,” IEEE Trans. Geosci. Remote Sensing, Vol. 27, pp. 687-697, 1989.
81. T. Mo, T.J. Schmugge, and T.J. Jackson, “Calculation of radar backscattering coefficient of vegetation-covered soil,” Remote Sens. Environ., Vol. 15, pp. 119-133, 1984.
82. H.J. Eom and A.K. Fung, “Scattering from a random layer embedded with dielectric needles,” Remote Sens. Environ., Vol. 19, pp. 139-149, 1986.
83. N.S. Chauhan, R.H. Lang, and K.J. Ranson, “Radar modelingof a boreal forest,” IEEE Trans. Geosci. Remote Sensing, Vol. 29, pp. 627-638, July 1991.
84. M.A. Karam, A.K. Fung, R.H. Lang , and N.S. Chauhan, “A microwave scattering model for layered vegetation,” IEEE Trans. Geosci. Remote Sensing, Vol. 30, pp. 767-784, 1992.
85. K.C. McDonald, M.C. Dobson, and F.T. Ulaby, “Modeling multi-frequency diurnal backscatter from a walnut orchard,” IEEE Trans. Geosci. Remote Sensing, Vol. 29, pp. 852-863, 1991.
86. S.S. Saatchi and K.C. McDonald, “Coherent effects in microwave backscattering models for forest canopies,” IEEE Trans. Geosci. Remote Sensing, Vol. 35, pp. 1032-1044, July 1997.
87. H.T. Chuah, S. Tjuatja, A.K. Fung, and J.W. Bredow, “Radar backscatter from a dense discrete random medium,” IEEE Trans. Geosci. Remote Sensing, Vol. 35, pp. 892-900, July 1997.
88. V.M. Finkelberg, “Wave propagation in a random medium. The correlation group method,” Soviet Physics JETP, Vol. 26, pp.268-277, 1968.
89. A. Ishimaru, Wave Propagation and Scattering in Random Media, Vol. 2, Academic, New York, 1978.
90. Yu.N. Barabanenkov, “Radiative transfer theory and multiple scattering by an ensemble of particles,” Sov. Phys. Usp., Vol.117, pp. 49-92, 1975.
91. B. Wen, L. Tsang, D.P. Winnerbrener, and A. Ishimaru, “Dense medium radiative transfer theory: comparison with experiment and application to microwave remote sensing and polarimetry,” IEEE Trans. Geosci. Remote Sensing, Vol. 28, pp. 46-59, 1990.
92. T.B.A. Senior, K. Sarabandy, and F.T. Ulaby, “Measuring and modeling the backscattering cross section of a leaf,” Radio Science, Vol. 22, pp. 1109-1116, 1987.
93. R. Schiffer and K.O. Thielheim, “Light scattering by dielectric needles and discs,” J. Appl. Phys., Vol. 50, No. 4, pp. 2476-2483, 1979.
94. M.A. Karam, A.K. Fung, and Y.M. M.Antar, “Electromagnetic wave scattering from some vegetation samples,” IEEE Trans. Geosci. Remote Sensing, Vol. 26, pp. 799-808, Nov. 1988.
95. H.C. van de Hulst, Light Scattering by Small Particles, Wiley, New York, 1957.
96. L. Tsang, J.A. Kong, and R.T. Shin, Theory of Microwave Remote Sensing, New York: Wiley-Interscience, 1985.
97. A.A. Chukhlantsev, “Scattering and absorption of microwave radiation by elements of plants,” Radiotekhnika i Elektronika (Eng. Transl. as Radio Eng. Electron. Phys.), Vol. 31, pp. 1095-1104, 1986 (In Russian).
98. L. Tsang and K.-H. Ding, “Polarimetric signatures of a layer of random nonspherical discrete scatterers overlying a homogeneous half-space based on first- and second-order vector radiative transfer theory,” IEEE Trans. Geosci. Remote Sensing, Vol. 29, pp. 242-253, Mar. 1991.
99. D.M. Le Vine, A. Schneider, R.H. Lang, and H.G. Carter, “Scattering from thin dielectric disks,” IEEE Trans. Antennas Propagat., Vol. 33, pp. 1410-1413, 1985.
100. A.A. Chukhlantsev, “Microwave emission from vegetation canopies,” Ph.D. dissertation, The Moscow Institute of Physics and Technology (State University), 1981 (in Russian).
101. S.S. Seker and A. Schneider, “Electromagnetic scattering from a dielectric cylinder of finite Length,” IEEE Trans. Antennas Propagat., Vol. 36, pp. 303-307, 1988.
102. J. Stiles and K. Sarabandi, “A scattering model for thin dielectric cylinder of arbitrary cross section and electrical length,” IEEE Trans. Antennas Propagat., Vol. 44, pp. 260-266, Feb. 1996.
103. E. Mougin, A. Lopes, and T. Le Toan, “Microwave propagation at X-band in cylindrical-shaped forest components: attenuation observations,” IEEE Trans. Geosci. Remote Sensing, Vol. 28, pp. 60-69, Jan. 1990.
104. A. Lopes and E. Mougin, “Microwave propagation in cylindrical-shaped forest components: interpretation of attenuation observations,” IEEE Trans. Geosci. Remote Sensing, Vol. 28, pp. 315-324, May 1990.
105. J.R. Wait, “Scattering of a plane wave from a circular dielectric cylinder at oblique incidence,” Can. J. Phys., Vol. 33, p. 189, 1955.
106. J.R. Wait, “The long wavelength limit in scattering from a dielectric cylinder at oblique incidence,” Can. J. Phys., Vol. 43, p. 2212, 1965.
107. Ch. Maetzler and A. Sume, “Microwave radiometry of leaves,” in Microwave Radiometry and Remote Sensing Applications, Ed., P.Pampaloni, VSP, Utrecht, The Netherlands, 1989.
108. F.T. Ulaby and M.A. El-Rayes, “Microwave dielectric spectrum of vegetation – part II: dual dispersion model,” IEEE Trans. Geosci. Remote Sensing, Vol. 25, pp. 550-557, Sept. 1987.
109. F.T. Ulaby and R.P. Jedlicka, “Microwave dielectric properties of plant material,” IEEE Trans. Geosci. Remote Sensing, Vol. 22, pp. 406-415, July 1984.
110. G.P. de Loor, “Dielectric properties of heterogeneous mixtures containing water,” J. Microwave Power, Vol. 3, pp. 67-73, 1960.
111. K.C. McDonald, R. Zimmermann, and J.K. Kimball, “Diurnal and spatial variations of xylem dielectric constant in Norway spruce (Picea abies [L.} Karst.) as related to microclimate, xylem sap flow, and xylem chemistry,” IEEE Trans. Geosci. Remote Sensing, Vol. 40, pp. 2063-2082, Sept. 2002.
112. R. DeRoo, Y. Kuga, M.C. Dobson, and F.T. Ulaby, “Bistatic radar scattering from organic debris of a forest floor,” Proc. of IGARSS’91 Symposium, Helsinki, June 3-6 1991, Vol. 1, pp. 15-18.
113. A. Stogrin, “Equation for calculating the dielectric constant of saline water,” IEEE Trans. Microwave Theory Tech., Vol. MIT-19, pp. 733-736, 1971.
114. A. Franchois, Y. Pineiro, and R.H. Lang, “Microwave permittivity measurements of two conifers,” IEEE Trans. Geosci. Remote Sensing, Vol. 36, pp. 1384-1395, Sept. 1998.
115. Ch. Maetzler, “Microwave dielectric model of leaves,” in Microwave Radiometry and Remote Sensing of Environment, Ed. D.Solimini, VSP, Utrecht, The Netherlands, 1995, pp. 389-390.
116. Ch. Maetzler, “Microwave (1-100 GHz) dielectric model of leaves,” IEEE Trans. Geosci. Remote Sensing, Vol. 33, pp. 947-949, 1994.
117. M.A. El-Rayes and F.T. Ulaby, “Microwave dielectric spectrum of vegetation – part I: experimental observations,” IEEE Trans. Geosci. Remote Sensing, Vol. 25, pp. 541-549, Sept. 1987.
118. Applied Microwave Corp., Manual for Portable Dielectric Probe, Lawrence, KS: Applied Microwave Corp., 1989.
119. N. Chauhan, R. Lang, J. Ranson, and O. Kilic, “Multi-stand radar modeling from a boreal forest: results from the Boreas intensive field campaign – 1993,” in Proc. IEEE IGARSS’94, Vol. 1, pp. 235-237.
120. N. Chauhan, R. Lang, J. Ranson, and O. Kilic, “Multi-stand radar modeling from a boreal forest: results from the Boreas intensive field campaign – 1993,” in Proc. IEEE IGARSS’95, Firenze, Italy, Vol. 2, pp. 981-983.
121. M.C. Dobson, “Diurnal and seasonal variations in the microwave dielectric constant of selected trees,” in Proc. IEEE IGARSS’88, Edinburgh, UK, Vol. 3, pp. 1754.
122. M.C. Dobson, R. de la Sierra, and N. Christensen, “Spatial and temporal variations of the microwave dielectric properties of loblolly pine trunks,” in Proc. IEEE IGARSS’91, Espoo, Finland.
123. K.C. McDonald, M.C. Dobson, and F.T. Ulaby, “Using MIMICS to model L-band multiangle and multitemporal backscatter from a walnut orchard,” IEEE Trans. Geosci. Remote Sensing, Vol. 28, pp. 477-491, July 1990.
124. W.A. Salas, K.J. Ranson, B.N. Rock, and K.T. Smith, “Temporal and spatial variations in dielectric constant and water status of dominant forest species from New England,” Remote Sens. Environ., Vol. 47, pp. 109-119, 1994.
125. K.C. McDonald, R. Zimmermann, J. Way, and W. Chun, “Automated instrumentation for continuous monitoring of the dielectric properties of woody vegetation: system design, implementation, and selected in situ measurements,” IEEE Trans. Geosci. Remote Sensing, Vol. 37, pp. 1880-1894, July 1999.
126. J. Way, J. Paris, M.C. Dobson, K.C. McDonald, et al, “Diurnal change in trees as observed by optical and microwave sensors: the EOS synergism study,” IEEE Trans. Geosci. Remote Sensing, Vol. 29, pp. 807-821, 1991.
127. H.S. Tan, “Microwave measurements and modeling of the permittivity of tropical vegetation samples, Appl. Phys., Vol. 25, pp. 351-355, 1981.
128. I.A. Shadrina, “Microwave dielectric properties of woody materials,” in Proc. of All-Russian Conference “Remote Sensing of terrain and atmosphere,” 2001, pp.237-241, (in Russian).
129. P. Selers, F. Hall, H. Margolis, et al, “The boreal ecosystem-atmosphere study (BOREAS): an overview of early results from the 1994 field year,” Bulletin of the American Meteorological Society, Vol. 76, pp. 1549-1577, 1995.
130. A.A. Chukhlantsev and S.P. Golovachev, “Estimates of 3…300 cm radio wave attenuation by vegetation canopies,” Lesnoi vestnik (Forest news), No. 1 (21), pp. 112-117, 2002 (in Russian).
131. L.-W. Li, J.-H. Koh, T.-S. Yeo, M.-S. Leong, and P.-S. Kooi, “Analysis of radiowave propagation in a four-layered anisotropic forest environment,” IEEE Trans. Geosci. Remote Sensing, Vol. 37, pp. 1967-1979, July 1999.
132. D.H. Hoekman, “Measurements of the backscatter and attenuation properties of forest stands at X-, C-, and L-band,” Remote Sensing Environ., Vol. 23, pp. 397-416, 1987.
133. D.E. Pitts, G.D. Badhwar, and E. Reyna, “The use of a helicopter mounted ranging scatterometer for estimation of extinction and scattering properties of forest canopies, part II: experimental results for high-density aspen,” IEEE Trans. Geosci. Remote Sensing, Vol. 26, pp. 144-152, 1988.
134. M. Murata, H. Aiba, K. Tonoike, J. Komai, H. Hirosava, and K. Nakada, “Experimental results of L-band microwave penetration properties of trees,” in Proc. IEEE IGARSS’87, pp.815-820.
135. H. Shinohara, T. Homma, H. Nohmi, H. Hirosava, and T. Tagawa, “Relation between L-band microwave penetration/backscattering characteristics and state of trees,” in Proc. IEEE IGARSS’92, pp.539-541.
136. M.T. Hallikainen, T. Tares, J. Hyyppa, E. Somersalo, P. Ahola, M. Toikka, and Pullianen, “Helicopter-borne measurements of radar backscatter from forests,” Int. J. Remote Sensing, Vol. 11, pp. 1179-1191, 1990.
137. F.T. Ulaby, M.W. Witt, and M.C. Dobson, “Measuring the propagation properties of a forest canopy using a polarimetric scatterometer,” IEEE Trans. Antennas Propagat., Vol. 38, pp. 251-258, 1990.
138. S.L. Durden, J.D. Klein, and H.A. Zebker, “Polarimetric radar measurements of a forested area near Mt. Shasta,” IEEE Trans. Geosci. Remote Sensing, Vol. 29, pp. 441-450, 1991.
139. J.W. Herbstreit and W.Q. Crichlow, “Measurement of the attenuation of radio signals by jungles,” Radio Sci., Vol. 68D, pp.903-906, 1964.
140. H.A. Whale, “Radio propagation through New Guinea rain forest,” Radio Sci., Vol. 3, No.10, p.1038, 1968.
141. R.K. Tewary, S. Swarup, and M.N. Roy, “Radio wave propagation through rain forest of India,” IEEE Trans. Antennas Propagat., Vol. 38, pp. 433-449, Apr. 1990.
142. T. Tamir, “On radio-wave propagation in forest environments,” IEEE Trans. Antennas Propagat., Vol. 15, pp. 806-817, Nov. 1967.
143. E.A. Vorobeichik, V.S. Petibskaia, A.A. Chukhlantsev, and G.G. Yazerian, “Microwave radiation of the rice fields,” Radiotekhnika i Elektronika (Eng. Transl. as Radio Eng. Electron. Phys.), Vol. 33, pp. 2420-2421, 1988 (In Russian).
144. S.P. Golovachev, E.A. Reutov, A.A. Chukhlantsev, and A.A. Shutko, “Experimental investigation of microwave emission of vegetable crops,” Izvestia VUZ’ov, Radiofizika (Engl. Transl. Radiophys, Quantum Electron.), Vol. 32, pp.551-556, 1989 (in Russian).
145. A.A. Chukhlantsev, “Microwave attenuation by coniferous branches,” Lesnoi vestnik (Forest news), No. 1 (21), pp. 110-112, 2002 (in Russian).
146. K. Ya.Kondratiev, V.V. Melentiev, and V.A. Nazarkin, Remote Sensing of Aqua Tories from Space, S.-Petersburg, Gidrometeoizdat, 1992 (in Russian).
147. Ch. Maetzler and U. Wegmuller, “Progress in multi-frequency radiometry of natural objects,” ESA/NASA International Workshop. VSP, Eds.: B.J. Choudhury, J.H. Kerr, E.G. Njoku, and P. Pampaloni, 1994, pp.345-355.
148. B.I. Vichev, E.N. Krasteva, and K.G. Kostov, “Study of seasonal evolution of tree emission using zenith-looking microwave radiometers,” in Proc. IEEE IGARSS’95, pp. 981-983.
149. A.A. Milshin, A.G. Grankov, and V.G. Mishanin, “Mapping of the temperature and moisture regime of forests,” Issledovanie Zemli iz Kosmosa (Research of the Earth from Space), No. 5, pp. 85-93, 1999 (in Russian).
150. G. Macelloni, S. Paloscia, P. Pampaloni, and R. Ruisi, “Airborne multifriquency L- to Ka- band radiometric measurements over forests,” IEEE Trans. Geosci. Remote Sensing, Vol. 39, pp. 2407-2513, Nov. 2001.
151. H. Hirosava, Y. Matsuzaka, and O. Kobayashi, “Measurement of microwave backscatter from a cypress with and without leaves,” IEEE Trans. Geosci. Remote Sensing, Vol. 27, pp. 698-701, 1989.
152. M. Murata, H. Aiba, K. Nakada, K. Tonoike, J. Komai, and H. Hirosava, “Experimental results of L-band microwave penetration properties of trees,” Proc. IUFRO S6.05/ISPRS, Commission 7, Joint session, pp. 75-84, 1988.
153. A.J. Sieber, “Forest signatures in imaging and non-imaging microwave scatterometer data,” ESA Journal, Vol. 9, pp. 431-448, 1985.
154. D.P. Belcher, Proc. EUSAR 2000, p. 141.
155. C. Varekamp and D.H. Hoekman, “High-resolution InSAR image simulation for forest canopies,” IEEE Trans. Geosci. Remote Sensing, Vol. 40, pp. 1648-1655, July 2002.
156. D.H. Hoekman and M.J. Quinones, “Biophysical forest type characterization in the Colombian Amazon by airborne polarimetric SAR,” IEEE Trans. Geosci. Remote Sensing, Vol. 40, pp. 1288-1300, June 2002.
157. J.T. Koskinen, J.T. Pulliainen, M.P. Maekynen, and M.T. Hallikainen, “Seasonal comparison of HUTSCAT ranging scatterometer and ERS-1 SAR microwave signatures of boreal forest zone,” IEEE Trans. Geosci. Remote Sensing, Vol. 37, pp. 2068-2079, July 1999.
158. J.T. Pulliainen, L. Kurvonen, and M.T. Hallikainen, “Multitemporal behavior of L- and C-band SAR observations of boreal forests,” IEEE Trans. Geosci. Remote Sensing, Vol. 37, pp. 927-937, March 1999.
159. T. Castel, A. Beaudoin, N. Floury, T. Le Toan, Y. Caraglio, and J.-F. Barczi, “Deriving forest canopy parameters for backscatter models using the AMAP architectural plant model,” IEEE Trans. Geosci. Remote Sensing, Vol. 39, pp. 571-583, March 2001.
160. W. Wagner, G. Lemoine, M. Borgeaud, H. Rott, “A study of vegetation cover effects on ERS scatterometer data,” IEEE Trans. Geosci. Remote Sensing, Vol. 37, pp. 938-948, March 1999.
161. M. Moghaddam, S.S. Saatchi, “Monitoring tree moisture using an estimation algorithm applied to SAR data from BOREAS,” IEEE Trans. Geosci. Remote Sensing, Vol. 37, pp. 901-916, March 1999.
162. F. Marliani, S. Paloscia, P. Pampaloni, and J.A. Kong, “Simulating coherent backscattering from crops during the growing cycle,” IEEE Trans. Geosci. Remote Sensing, Vol. 40, pp. 162-177, Jan. 2002.
163. A.Y. Nashashibi, F.T. Ulaby, P. Frantzis, and R.D. De Roo, “Measurements of the propagation parameters of tree canopies at MMW frequencies,” IEEE Trans. Geosci. Remote Sensing, Vol. 40, pp. 298-304, Feb. 2002.
164. R. Magagi, M. Bernier, and C.-H. Ung, “Quantitative analysis of RADARSAT SAR data over a sparse forest canopy,” IEEE Trans. Geosci. Remote Sensing, Vol. 40, pp. 1301-1313, June 2002.