INFLUENCE OF LIGHT SCATTERING BY 3D-IRREGULARITIES ON THE CHARACTERISTICS OF THE INTEGRATED OPTICAL DEVICES USING FOR OPTICAL SIGNAL PROCESSING
A. A. Egorov
A.M. Prokhorov General Physics Institute of RAS
Received February 20, 2008
We analysis and discuss an influence of 3D waveguide's scattering on some characteristics of the integrated optical devices: attenuation in optical waveguides, threshold-pumping power for thin-film dye lasers, and dynamic range of integrated optical spectrum analyzer.
1. IntroductionThe integrated optical waveguide [1-21] is a basis for formation of various integrated optical circuits e.g.: RF-spectrum analyzer, interferometer, multiplexer/demultiplexer, focusing, dispersive and filtering components, and other integrated optical elements performing correlation and another optical signal processing operations. The major factor limiting critical power characteristics of optical integrated circuits are losses and, in particular, the power losses of an optical signal due to scattering on the structure’s irregularities of waveguide's part [1-4] of optical integrated circuits.
Influence of waveguide optical 3D-scattering on the threshold-pumping power for thin-film dye laser and on the integrated optical RF-spectrum analyzer dynamic range [16] are also the most known effects limiting the characteristics of optical integrated circuits. We use in this work an analysis of electrodynamics’ scattering problem of the directed TE0-mode in an integrated-optical waveguide containing statistic irregularities in the presence of noise which is presented in our papers [12-15].
In OIC with a high degree of integration, undoubtedly, it is most promising to use the laser made on the same uniform substrate of a waveguide [3]. We shall estimate influence of the power losses due to 3D-scattering on limiting threshold pumping power in the optical integrated circuits of two types: the ring thin-film waveguide's laser and the thin-film waveguide's laser with active substance from the dye POPOP.
2. Estimation of limiting threshold-pumping power for thin-film waveguide lasers with regard to three-dimensional scattering and bulk lossesA full analysis of electrodynamics’ problem of scattering of the directed waveguide mode in an integrated optical waveguide containing arbitrary irregularities in presence of noise is presented in our papers [12-15]. This will make it possible to study the scattering of electromagnetic waves in irregular waveguides and applied these results to 3D integrated OIC.
To analyze the laser generation and scattering in the thin-film dye laser with the distributed feedback the known Bragg formula is used [3, 20]:
where Λ is the period of the lattice made on a substrate of a waveguide, γ is the effective refraction parameter of a waveguide for a considered mode, m is the order of diffraction,
is the angle of incidence on waveguide grating. Because of difficulties of manufacturing of a diffractive lattice of the first order (m = 1) the lattice of the third order is usually used.
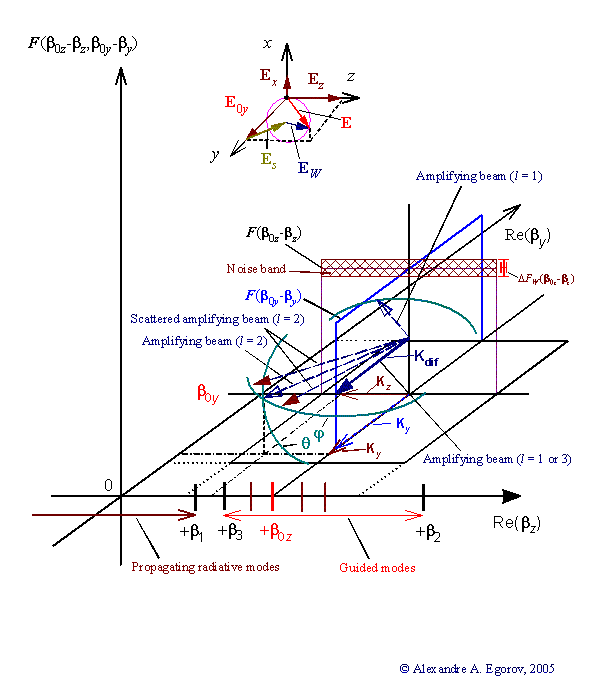
On the Fig. 1 the vectors of diffracted (amplifying) and scattered waves for the case l = 1 or 3 and l = 2 are presented accordingly (l is the order of Bragg diffraction). This figure illustrate clearly the phenomenon of scattering of an amplifying mode with l = 3 in the plane of waveguide (in-plane-scattering) over the angle φ (amplifying and scattered beams with l = 1 and 2) and scattering over the angle θ (scattering in the incident plane). These two types of scattering are in total the 3D-scattering of an amplifying laser mode.
Fig. 1 illustrates the phenomenon of scattering of an amplifying mode with l = 3 in the plane of waveguide (in-plane-scattering) over the angle φ (amplifying and scattered beams with l = 1 and 2) and scattering over the angle θ (scattering in the incident plane). These two types of scattering are in total the 3D scattering of an amplifying laser mode.
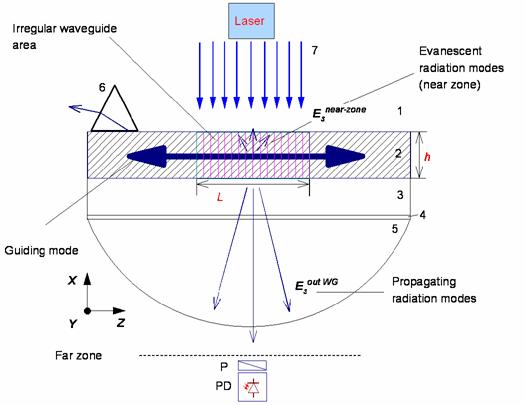
The thin-film waveguide's laser (Fig. 2) with the distributed feedback is made, for example, by dissolution of the dye POPOP in a polystyrene film. In this case the maximum of a luminescence of this dye is about on the wavelength λ = 0.43 microns (violet part of the visible spectrum of radiation), and the width of the luminescence spectrum is approximately 650 Å. The ultra-violet nitric laser (λ = 0.34 microns) is used for the pumping.
As is known, the dye’s lasers are very perspective for application in lines of optical communication, in metrology, and also for application in biomedical and ecological researches with the purpose of the spectral analysis of substances, for example, in integrated-optical sensors of gases and liquids concentration [17-19].
It is connected first with an opportunity of frequency variation of coherent radiation of thin-film dye lasers. Generally, the interval of frequency changing of the generation line of the concrete dye laser is determined by the time dependence of a pumping source. This interval can be increased, if instead the pumping with continuous excitation one uses the pumping with the short impulse excitation.
We estimate limiting threshold pumping power
for the ring thin-film laser on dye POPOP under the known formula [20, 21]. In result it is received an estimated value for limiting threshold pumping power
≈ 18 W. The power at which generation of the thin-film dye laser began in experiments is approximately
≈ 40 W that is in 2.2 times grater than
[20].
In our opinion such divergence of the data results from the three-dimensional character of waveguide's scattering [1-15], and is caused also by the losses of waveguide mode power due to scattering on waveguide bulk inhomogeneities. One should take into account both of these factors when trying to find correct estimate for limiting threshold-pumping power
.
Taking into account 3D scattering (see in detail in our articles [12-15]), we receive the following correct estimation for full three-dimensional coefficient of attenuation
≈ 1.25-1.67 cm-1 at a variation of radius of correlation in an interval ≈ 0.5-2 microns. Based on bulk losses (
≈ 0.15 cm-1) and three-dimensional character of scattering the estimation for threshold pumping power is
≈ 30-36 W. Apparently this estimation differs from experimentally measured value approximately on 10-25%. Thus, the account of three-dimensional character of waveguide's scattering of laser radiation and bulk losses on the average has allowed lowering an error of a theoretical estimation of limiting threshold-pumping power from 55% up to ≈ 18%.
The estimation of limiting threshold-pumping power for the thin-film dye laser with the distributed feedback may be made under the similar formula [20, 21]. Note that experimental value of threshold power was
≈ 45 W [20], i.e. it differs from our estimation approximately on 7%. In the paper [20] it have been received an estimate
≈ 6.4 W, which differs from the experimental value on 86%.
Taking into account of three-dimensional character of scattering on an anisotropic lattice (∂/∂y ≈ 0, therefore up to ≈ 90-95% of the power of a radiation of waveguide's mode scattered on a lattice remains in the plane of incidence and it is possible to put:
) allows us to specify estimation for threshold-pumping power:
≈ 44 W.
Hence, in this case the account of three-dimensional character of waveguide's scattering of laser radiation allows also lowering an error of the theoretical estimation of limiting threshold-pumping power from 7% up to ≈ 2%.
Fig. 1. The 3D-geometry of the waveguide scattering of a laser radiation, where: β0z is the module of the vector β0z of the incident TE-mode; βi = kni is the propagating constant, k = 2π/λ (i = 1, 2, 3), ni is the refractive indexes of the waveguide layers; F is the spectral density function of the waveguide irregularities in the appropriate direction, ΔF is the noisy fluctuations of F. In the above inset the total field E and there components of incident TE0-mode, scattering waves and a noise (E0y, Es and EW) are presented.
Fig.2. Cross section of the thin-film dye laser with the distributed feedback and the scheme of registration of the laser radiation scattered in an irregular integrated-optical waveguide which is formed by the media 1, 2, and 3. On the Fig. 2: 1 is the covering medium (air); 2 is the waveguide's layer (the polystyrene film activated by dye POPOP); 3 is the glass substrate; 4 is thin immersion layer; 5 is the quartz hemisphere; 6 is the prism; 7 is the pumping radiation; L is the length of irregular area containing the lattice; h is the waveguide thickness; P is the polarizer; PD is the photodetector.
3. ConclusionOur estimation of limiting threshold pumping power Pthr for a ring thin-film laser on dye POPOP with given parameters differs from the experimentally measured value approximately on 10–25%. It is allowed lowering an average error of a theoretical estimation of the limiting threshold-pumping power from 55% (for 2D-scattering theory) up to 18% (for 3D-scattering theory). The same estimation of limiting threshold-pumping power is performed for the thin-film dye laser with the distributed feedback. Experimental value of the threshold power differs from our estimation approximately on 7%.
The necessity of accurate estimations of losses in the various optical integrated circuits (optical processors etc.) are stipulated in particular by fast progress in telecommunication technologies, where the low losses of processing and signaling on large distances are required.
On the other hand, active development of nanotechnologies, doubtlessly, will increase requests to limiting performances of such devices as waveguides, filters, deflectors, lasers, photo detectors and other devices, integrated on a uniform substrate of the optical processor.
References
1. Marcuse D. Light Transmission Optics. – New York: Van Nostrand, 1972.
2. Sodha M.S., Ghatak A.K. Inhomogeneous optical waveguides. – London: Plenum Press, 1977.
3. Hunsperger R.G. Integrated Optics: Theory and Technology. – New York: Springer-Verlag, 1984.
4. Snyder A.V., Love J.D. Optical waveguide theory. – New York: Chapman and Hall, 1983.
5. Walter D.J., Houghton J. Attenuation in thin film optical waveguides due to roughness-induced mode coupling // Thin Solid Film. 52. pp. 461-476 (1978).
6. Ames G.H., Hall D.C. Attenuation in planar optical waveguides: comparison of theory and experiment // IEEE J. of QE. 19 (5). pp. 845-853 (1983).
7. Singh J., Richard M. de La Rue. An experimental study of in-plane light scattering in titanium diffused Y-cut LiNbO optical waveguides // J. of Lightwave Technology. 3 (1). pp. 67-76 (1985).
8. Smith C.J.M., Benisty H., Olivier S., Rattier M., Weisbuch C., Krauss T. F., De La Rue R. M., Houdre R., Oesterle U. Low-loss channel waveguides with two-dimensional photonic crystal boundaries // Appl. Phys. Lett. 77 (18). pp. 2813-2815 (2000).
9. Cowan A.R., Paddon P., Pacradouni V., Young J.F. Resonant scattering and mode coupling in twodimensional textured planar waveguides // JOSA. A. 18 (5). pp. 2090-2101 (2001).
10. Paulus M., Martin Oliver J.F. Light propagation and scattering in stratified media: a Green’s tensor approach // JOSA. A. 18 (4). pp. 854-861 (2001).
11. Hadley G.R. Out-of-plane losses of line-defect photonic crystal waveguides // IEEE Phot. Tech. Lett. 14. pp. 642-644 (2002).
12. Egorov A.A. Reconstruction of the experimental autocorrelation function and determination of the parameters of the statistical roughness of a surface from laser radiation scattering in an integrated-optical waveguide // Quantum Electronics. 33 (4). pp. 335-341 (2003).
13. Egorov A.A. Use of waveguide light scattering for precision measurements of the statistical parameters of irregularities of integrated optical waveguide materials // Opt. Eng. 44 (1). pp. 014601-1–014601-10 (2005).
14. Egorov A.A. Theory of the waveguide light scattering in integrated optical waveguide in presence of noise // Radiophysics and Quantum Electronics. 48 (1). pp. 57-67 (2005).
15. Egorov A.A. Vector theory of the waveguide scattering of laser radiation in the presence of noise (method of modes and method of Green’s function) // Las. Phys. 14 (8). pp. 1072-1080 (2004).
16. Boyd J.T., Anderson D.B. Effect of waveguide optical scattering on the integrated optical spectrum analyser dynamic range // IEEE J. of QE. 14 (6). pp. 437-443 (1978).
17. Chekhlova T. K., Timakin A. G., Popov K. A. Waveguide sensors for measuring concentrations of components in gas mixtures and liquids // Instruments and Experimental Techniques. 45 (2). pp. 281-284 (2002).
18. Egorov A.A., Egorov M.A., Tsareva Yu.I., and Chekhlova T.K. Study of the integrated-optical concentration sensor for gaseous substances. Laser Physics. 17. pp. 50-53 (2007).
19. Egorov A.A., Egorov M.A., Smoliakov R.B., Chekhlova T.K., Timakin A.G. Integrated-optical low-loss PbO2 diffusion waveguide sensitive chemical sensor. Journal of Radio Electronics. N 5 (2007).
20. Gilermo A., Kolbin I.I., Cheremiskin I.V. Tonkoplenochnye lazery na krasitele POPOP. Izvestiia. Vysshich uchebn. zaved. Radioelectronika. 21 (10). pp. 133-134 (1978).
21. Nakamura M., Yariv A., Yen H.W., Somekh S., Garvin H.L. Optically pumped GaAs surface laser with corrugation feedback. Appl. Phys. Lett. 22 (10). pp. 515-516 (1973).