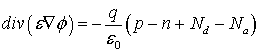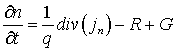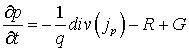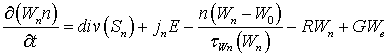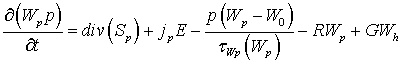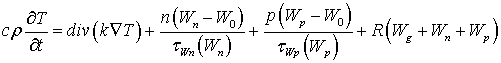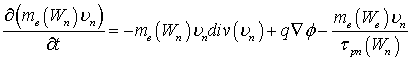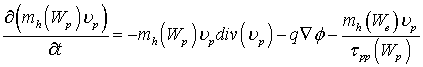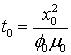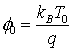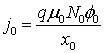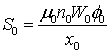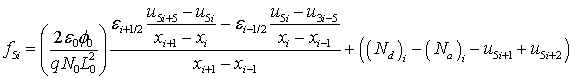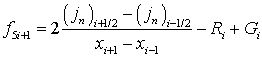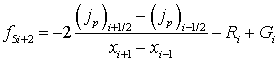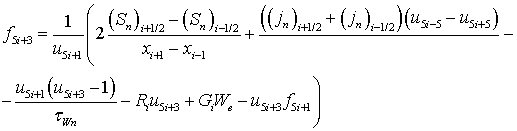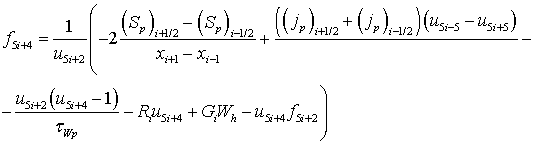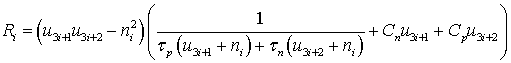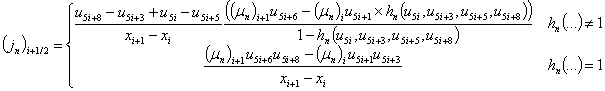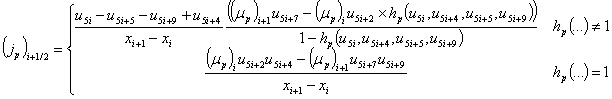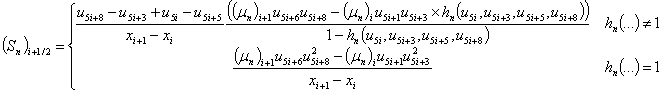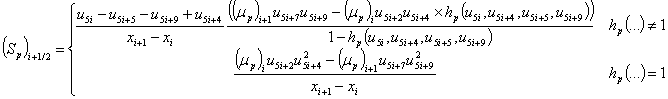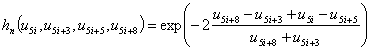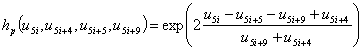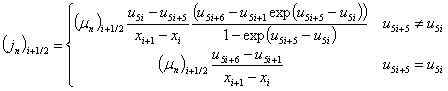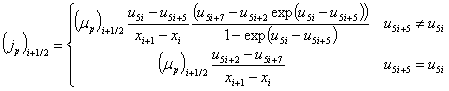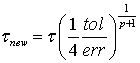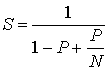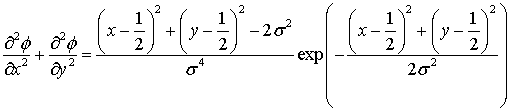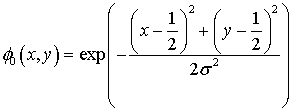УДК 004.4, 517.929, 621.382
Параллельные вычисления в задачах физико-топологического моделирования физических процессов в перспективных полупроводниковых приборах с учетом радиационного воздействия
В. К. Киселев, С. В. Оболенский, А. С. Пузанов, А. В. Скупов
ННГУ им. Н.И. Лобачевского
Статья получена 10 февраля 2014 г.
Аннотация. В работе представлены результаты применения параллельных вычислений на графических процессорах при решении задачи переноса носителей заряда в полупроводниковых приборах с учетом радиационного воздействия. На примере квазигидродинамической модели последовательно рассмотрены сведение системы уравнений в частных производных к дифференциально-алгебраической задаче и численные методы ее решения. На примере решения тестовой задачи показана эффективность рассмотренных алгоритмов.
Ключевые слова: физико-топологическое моделирование полупроводниковых приборов, квазигидродинамическое приближение, параллельные вычисления на графических процессорах, численное решение систем дифференциально-алгебраических уравнений, моделирование радиационного воздействия на полупроводниковые приборы.
Abstract. The paper presents the results of parallel computing on GPUs for the solving of the problem of charge transport in semiconductor devices taking into account the radiation effect. By the example of quasi-hydrodynamic model, the reduction of partial differential equations to the differential-algebraic problem and numerical methods for solving it are consistently considered. The efficiency of the considered algorithms is shown by the example of the the test problem solution.
Key words: physical and topological modeling of semiconductor devices, quasi-hydrodynamic approximation, parallel computing on graphics processors, numerical solution of differential-algebraic equations, modeling of radiation effects on semiconductor devices.
1. Введение
Начало исследований в области радиационной физики полупроводниковых приборов приходится на 60-е года XX века и обусловлено: активным внедрением дискретных элементов в военные и космические системы, успехами в радиационной физике твердого тела, появлением лабораторных источников проникающих излучений и другими факторами. Обзоры становления этой области науки и техники представлены в классических монографиях [1,2].
В это время появляются первые аналитические модели реакции полупроводниковых приборов на радиационное воздействие. Однако такого рода модели принципиально не могут учесть нелинейные эффекты, связанные с высоким уровнем инжекции и фотовозбуждения неравновесных носителей заряда в полупроводниковых структурах.
Строгий расчет переходных ионизационных процессов при высоких концентрациях неравновесных носителей заряда можно провести только на основе численного моделирования. Впервые данная задача была решена в работе [3] на основе диффузионно-дрейфового приближения. Однако итерационный алгоритм, основанный на поочередном решении разностных аналогов уравнения Пуассона и уравнений непрерывности для электронов и дырок [4], имеет низкую скорость сходимости вдали от состояния равновесия, что ограничивает его применимость при высоких уровнях инжекции или фотовозбуждения.
Еще в 60-е годы стало ясно, что диффузионно-дрейфовое приближение не позволяет корректно рассчитывать перенос носителей заряда в коротких структурах. Это обусловлено инерционностью электронно-дырочного газа, не учитываемой в диффузионно-дрейфовой модели. Для преодоления этого недостатка был разработан ряд моделей [5], носящих обобщенное название квазигидродинамические.
Впервые о решении задачи моделирования переноса носителей заряда в квазигидродинамическом приближении при радиационном воздействии сообщено в обзоре [6]. В указанной работе для учета разогревающего воздействия потока квантов высоких энергий в уравнения баланса энергии введено дополнительное слагаемое, учитывающее данный эффект. Позднее [7], в систему уравнений квазигидродинамической модели были добавлены уравнения баланса импульса электронного и дырочного газа, позволяющие учесть дополнительное рассеяние носителей заряда на кластерах радиационных дефектов. Однако для численного решения по-прежнему был использован алгоритм Гуммеля.
В работе [8] пространственно-дискретизированная диффузионно-дрейфовая модель представлена как система дифференциально-алгебраических уравнений. Данный подход позволил применить к решению задачи переноса носителей заряда жестко-устойчивые методы Гира [9] высокого порядка точности. Отмечается [8], что подход на основе метода прямых к решению задач моделирования физических процессов в полупроводниковых приборах представляется эффективным в связи с использованием при интегрировании возникающих систем дифференциально-алгебраических уравнений стандартных пакетов математических программ, предусматривающих:
− автоматический выбор шага интегрирования и порядка точности метода при заданной относительной ошибке;
− возможность использования стандартных программ для решения возникающих линейных уравнений с разреженной матрицей коэффициентов, что особенно ценно при решении многомерных задач;
− достаточно широкие возможности по изменению параметров алгоритма, что позволяет пользователю наилучшим образом подстраивать программу под конкретную задачу.
Анализ вышеизложенных тенденций развития численного моделирования переноса носителей заряда в полупроводниковых приборах при радиационном воздействии показывает, что объем вычислений увеличивается с уменьшением размеров рабочей области элемента. Это обусловлено как увеличением числа уравнений модели, так и уменьшением временного шага интегрирования системы уравнений переноса при переходе от диффузионно-дрейфового к квазигидродинамическому приближению. Последнее связано с тем, что характерное время изменения концентраций электронов и дырок в диффузионно-дрейфовой модели определяется их временами жизни, а характерное время изменения их средних энергий (характеристика электронно-дырочного газа, не учитываемая в диффузионно-дрейфовой модели) в квазигидродинамической модели определяется временами релаксации энергии и импульса. Учитывая, что времена жизни носителей заряда лежат в пределах 10-3…10-9 с, а времена релаксации энергии и импульса электронно-дырочного газа – 10-12…10-13 с, характерное уменьшение временного шага интегрирования составляет как минимум 4 порядка. Данное положение подтверждается путем анализа результатов численного моделирования.
Столь резкое увеличение объема вычислений требует применения радикальных мер повышения производительности, основным из которых в настоящее время является распараллеливание численных алгоритмов. Использование стандартных библиотек программ решения систем дифференциальных, нелинейных и линейных алгебраических уравнений, многие из которых содержат эффективные параллельные алгоритмы, определяет применение данного подхода в области высокопроизводительных вычислений на супер-ЭВМ в качестве базового.
2. Физико-топологическое моделирование реакции полупроводниковых приборов на воздействие проникающих излучений
Физико-топологическое моделирование важно как для понимания физических процессов, протекающих в полупроводниковых приборах, в том числе при радиационном воздействии, так и для оптимизации их конструкции с целью достижения наилучших характеристик. Именно моделирование отражает эволюцию представлений о том, как работает транзистор при различных его размерах [10]. Для микронных размеров диодов и транзисторов, когда длина свободного пробега была гораздо меньше длины области пространственного заряда p-n перехода, базы биполярного транзистора и канала полевого транзистора, используется представление о том, что в рабочей области полупроводникового прибора протекает заряженная жидкость, и для описания такого ламинарного течения применяются гидродинамические модели: диффузионно-дрейфовая, электротепловая и квазигидродинамическая. Для субмикронных размеров элементов, когда длина свободного пробега носителей заряда уже оказывается сопоставимой с характерным масштабом изменения потенциала и напряженности электрического поля, более реалистичными оказываются представления о частицах, пролетающих через активную область прибора. Для описания переноса носителей заряда в этом случае используется кинетическое уравнение Больцмана. Отметим, что семейство гидродинамических моделей переноса носителей заряда может быть формально получено из кинетического уравнения Больцмана с использованием ряда упрощающих предположений [11].
Границей применимости кинетического уравнения Больцмана и метода Монте-Карло как процедуры его решения [11] является рабочая область прибора, меньшая длины волны де Бройля для электронов и дырок. В этом случае активная область прибора ведет себя как волновод, для корректного описания которого необходимо использовать уравнение Шредингера. Такой полупроводниковый прибор становится квантовым, хотя на внешних электродах измеряются классические значения токов и напряжений.
В данном обзоре мы ограничимся рассмотрением гидродинамических моделей переноса носителей заряда и методов их распараллеливания. Так отмечалось во введении, существует большое количество вариантов формулировок систем уравнений, описывающих перенос носителей заряда в гидродинамическом приближении. Каждая модель содержит уравнение Пуассона и набор уравнений непрерывности (баланса). В таблице представлены основные системы уравнений переноса носителей заряда в полупроводниковых приборах.
Таблица 1. Иерархия гидродинамических моделей переноса носителей заряда
|
Модель
Уравнение |
Диффузионно-дрейфовая (локально-полевая) |
Электротепловая |
«Усеченная» квазигидродинамическая |
«Полная» квазигидродинамическая |
|
Пуассона |
+ |
+ |
+ |
+ |
|
Непрерывности электронов и дырок |
+ |
+ |
+ |
+ |
|
Теплопроводности кристаллической решетки |
|
+ |
+ |
+ |
|
Баланса энергии электронов и дырок |
|
|
+ |
+ |
|
Баланса импульса электронов и дырок |
|
|
|
+ |
Наиболее полное описание переноса в гидродинамическом приближении (так называемая «полная» квазигидродинамическая модель) включает в себя: уравнение Пуассона, уравнения непрерывности для электронов и дырок, уравнения баланса энергии электронов, дырок и кристаллической решетки, уравнения баланса импульса электронов и дырок и уравнения плотностей токов и потоков энергии электронов и дырок
|
(1) |
|
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
|
|
(6) |
|
|
(7) |
|
|
(8) |
|
|
(9) |
|
|
(10) |
|
|
(11) |
|
|
(12) |
где φ – потенциал электрического поля, n – концентрация электронов; p – концентрация дырок, T – температура кристаллической решетки, Wn – средняя энергия электронов, Wp – средняя энергия дырок, un – дрейфовая скорость электронов, up – дрейфовая скорость дырок, jn – плотность электронного тока, jp – плотность дырочного тока, Sn – плотность потока энергии электронов, Sp – плотность потока энергии дырок, Dn – коэффициент диффузии электронов, Dp – коэффициент диффузии дырок, tWn – время релаксации энергии электронов, tWp – время релаксации энергии дырок, We – равновесная энергия носителей заряда, We – средняя энергия радиационно-генерируемых электронов, Wh – средняя энергия радиационно-генерируемых дырок, Nd – концентрация положительно заряженных ионов примеси, Na, – концентрация отрицательно заряженных ионов примеси, e0 – диэлектрическая проницаемость вакуума, e – диэлектрическая проницаемость полупроводника, R – коэффициент рекомбинации, G – коэффициент генерации, k – теплопроводность, c – удельная теплоемкость, r – плотность, me – эффективная масса электронов, mh – эффективная масса дырок, tpn – время релаксации импульса электронов, tpp – время релаксации импульса дырок.
В «усеченной» квазигидродинамической модели (модели локальной температуры) уравнения баланса импульсов электронов (7) и дырок (8) отсутствуют. В связи с этим средняя дрейфовая скорость электронов и дырок становятся функцией их средней энергии un(Wn) и up(Wp), соответственно.
В электротепловой модели электрофизические параметры полупроводника становятся функциями напряженности электрического поля и температуры кристаллической решетки, а уравнения баланса энергии электронов (4) и дырок (5) исключаются. В диффузионно-дрейфовой модели моделирование переноса носителей заряда проводится при фиксированной температуре полупроводникового прибора и уравнение теплопроводности (6) также исключается.
Для учета воздействия проникающих излучений при моделировании переноса носителей заряда в уравнения непрерывности электронов (2) и дырок (3) вводится слагаемое, отвечающее за генерацию неравновесных носителей заряда, в уравнения баланса энергии добавлено слагаемое, отвечающее за разогрев электронно-дырочного газа, а электрофизические параметры полупроводника зависят от потоков дефектообразующих излучений.
3. Численные методы решения задачи переноса носителей заряда в полупроводниковых приборах при воздействии проникающих излучений
3.1. Нормировка и выбор базиса переменных системы уравнений переноса носителей заряда
При построении численных алгоритмов удобно пользоваться системой уравнений переноса носителей заряда, приведенной к безразмерному виду. Это позволяет не только уменьшить мантиссы обрабатываемых чисел до приемлемых величин, пригодных для цифровой обработки, что особо актуально для вычислительных архитектур, использующих числа одинарной точности (например, технология параллельных вычислений CUDA корпорации NVidia [12-15]), но также избавиться от некоторых постоянных размерных коэффициентов в уравнениях модели. Нормировочные коэффициенты, используемые в работе, приведены в таблице 2.
Таблица 2. Нормировка переменных уравнений переноса носителей заряда
|
Модель переноса |
Нормируемая величина |
Условное обозначение |
Нормировочный коэффициент |
||
|
Квазигидродинамическая модель |
Электротепловая модель |
Диффузионно-дрейфовая модель |
Пространство |
x |
x0 |
|
Время |
t |
|
|||
|
Подвижность |
μn, μp |
|
|||
|
Концентрация |
n, p, Nd, Na |
|
|||
|
Потенциал |
φ |
|
|||
|
Плотность тока |
jn, jp |
|
|||
|
|
Температура |
T |
T0 |
||
|
|
|
Энергия |
Wn, Wp |
|
|
|
Плотность потока энергии |
Sn, Sp |
|
|||
Искомыми функциями при решении системы уравнений переноса носителей заряда являются зависимости от координат и времени
− в диффузионно-дрейфовом приближении: потенциала электрического поля и концентрации электронов и дырок;
− в электротепловом приближении: потенциала электрического поля, концентрации электронов и дырок и температуры кристаллической решетки;
− в квазигидродинамическом приближении: потенциала электрического поля, концентрации электронов и дырок, температуры кристаллической решетки, средней энергии электронов и дырок
при заданных зависимостях электрофизических параметров полупроводника, начальных и граничных условиях.
Множество исходных функций системы уравнений переноса носителей заряда принято называть базисом переменных. В диффузионно-дрейфовом приближении распространены три базиса:
− {φ, n, p} – потенциал электрического поля, концентрации электронов и дырок;
− {φ, φn, φp} – потенциал электрического поля, квазиуровни Ферми для электронов и дырок;
− {φ, Φn, Φp} – потенциал электрического поля, экспоненты квазиуровней Ферми для электронов и дырок.
В электротепловом и квазигидродинамическом приближениях принято использовать базисы {φ, n, p, T} и {φ, n, p, T, Wn, Wp}, {φ, n, p, T, Wn, Wp, un, up}, соответственно.
3.2. Сведение системы уравнений переноса носителей заряда к дифференциально-алгебраической системе уравнений
Любая система дифференциальных уравнений в частных производных параболического и эллиптического типов, к числу которых относится семейство систем уравнений переноса носителей заряда в полупроводниках, может быть сведена к системе дифференциально-алгебраических уравнений вида
|
(13) |
путем дискретизации пространственной части уравнений в частных производных. В выражении (13) u – вектор нормированных искомых переменных, M – матрица массы, f – векторная функция нормированных пространственно-дискретизированных правых частей системы уравнений переноса носителей заряда, t – нормированное время.
В настоящее время применяются 3 метода пространственной дискретизации:
− конечных объемов (FVM);
− конечных элементов (FEM);
− конечных разностей (FDM).
Дискретизация определяется формой записи системы дифференциальных уравнений в частных производных: для дифференциальной формы записи дискретизация осуществляется при помощи конечно-разностных методов; интегральная форма записи дискретизируется при помощи метода конечных объемов, а вариационная форма – при помощи метода конечных элементов.
Методы дискретизации, их преимущества и недостатки, широко рассмотрены в литературе. Применительно к одномерной квазигидродинамической модели переноса носителей заряда, рассматриваемой ниже, явным преимуществом будет обладать метод конечных разностей. Основной акцент сделаем на дискретизации плотностей токов и потоков энергии носителей заряда. Поэтому без ущерба общности обсуждения дальнейших результатов исключим из системы (1)-(12) уравнения баланса импульса электронов и дырок, а также уравнение теплопроводности кристаллической решетки.
На отрезке [0, 1] введем неравномерную пространственную сетку с узлами x = {xi}, i = 0, 1,…, N – 1, согласованную с распределением легирующей примеси: вблизи границ раздела и контактов полупроводникового прибора шаг сетки делаем более мелким. Определим значения базисных функций {φ, n, p, Wn, Wp} в следующем виде: u = {ui}, u5i = φi, u5i+1 = ni, u5i+2 = pi, u5i+3 = (Wn)i, u5i+2 = (Wp)i. Тогда векторная функция нормированных пространственно-дискретизированных правых частей системы уравнений переноса носителей заряда в квазигидродинамическом приближении записывается в виде
|
(14) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а матрица массы становится диагональной с элементами m5i,5i = 0, m5i+1,5i+1 = 1, m5i+2,5i+2 = 1, m5i+3,5i+3 = 1, m5i+4,5i+4 = 1.
Дискретные аналоги плотностей токов и потоков энергии электронов и дырок определяются в ячейках сетки на основе аппроксимации Шарфеттера-Гуммеля (SG) [16], позволяющей сохранить монотонность численной схемы независимо от величины шага пространственной дискретизации и имеющей ряд особенностей для квазигидродинамического приближения [17]
|
|
(15) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отметим, что если положить равенство средних энергий электронов и дырок тепловой энергии носителей заряда в каждом узле расчетной сетки u5i+3 ≡ u5i+4 ≡ 1 и, следовательно, постоянные их подвижности μi ≡ μi+1 ≡ μi+1/2, то выражения для плотностей токов переходят в традиционный для диффузионно-дрейфовой модели вид
|
|
(16) |
|
|
3.3. Методы решения системы дифференциально-алгебраической уравнений
Любая гидродинамическая модель переноса носителей заряда в полупроводнике включает уравнение Пуассона, определяющее алгебраическую компоненту дискретизированной задачи (13). Матрица массы дифференциально-алгебраических уравнений является вырожденной, что определяет «бесконечную жесткость» задачи (13) (в терминах работы [18]). При построении разностных схем для жестких систем предъявляются повышенные требования к устойчивости решения – явные схемы для решения жестких задач требуют очень мелкого шага интегрирования и поэтому практически неприменимы.
3.3.1. Неявные итерационные схемы
Среди неявных схем широко распространены методы Рунге-Кутты (IRK – implicit Runge-Kutta methods). Не все схемы Рунге-Кутты подходят для решения жестких задач. В монографии [19] дан всеобъемлющий обзор методов Рунге-Кутты, пригодных для решения жестких задач, выделены методы, являющиеся жестко точными, то есть сохраняющими при решении систем дифференциально-алгебраических уравнений тот же порядок точности, что и для систем дифференциальных уравнений.
Любой неявный метод Рунге-Кутты для перехода на новый временной слой требует решения системы нелинейных алгебраических уравнений при помощи итераций ньютоновского типа. Для s-стадийного неявного метода Рунге-Кутты минимальное число возникающих нелинейных систем s соответствует диагонально неявным методам (DIRK – diagonal implicit Runge-Kutta methods). Именно они чаще всего и используются на практике.
Неявные многошаговые методы (формулы дифференцирования назад) положены в основу популярных программ Гира. Коэффициенты многошаговых методов подбираются так, чтобы q-шаговый метод имел точность O(tq). Однако можно показать [19], что неявные многошаговые методы с q > 2 теряют свойство безусловной устойчивости. При q > 6 неявные многошаговые методы становятся абсолютно неустойчивыми. Этим неявные многошаговые методы сильно уступают неявным методам Кунге-Кутты. Тем не менее, неявные многошаговые методы первого и второго порядков (неявный метод Эйлера и неявное правило трапеций) реализованы в системе автоматизированного проектирования изделий микроэлектроники TCAD Sentaurus фирмы Synopsys [20] для решения задачи переноса носителей заряда. Также на базе методов Гира реализован комплекс программ оценки радиационного воздействия на изделия микроэлектроники DIODE-2D разработки НИЯУ МИФИ [8].
Наличие итераций сильно усложняет использование неявных методов Рунге-Кутты и многошаговых методов, так как к проблемам устойчивости добавляется проблема сходимости итерационного процесса при решении систем нелинейных алгебраических уравнений. Альтернатива, которая обходит эту трудность – методы типа Розенброка (ROS) и Розенброка-Ваннера (ROW) [18,19]. Формально эти схемы неявные, но итераций в них не возникает и число арифметических действий для перехода на новый временной слой фиксировано и заранее известно (как в явных схемах). За это безусловное преимущество эти схемы получили название явно-неявных или полунеявных.
Формулы перехода на новый временной слой однопараметрического семейства одностадийных схем Розенброка имеют вид [21]
|
|
(17) |
где ![]() –
матрица Якоби, t – шаг по времени, u
– решение на текущем временном слое,
–
матрица Якоби, t – шаг по времени, u
– решение на текущем временном слое, ![]() – решение на новом
временном слое, a – числовой параметр, определяющий
свойства схемы. При a = 0 это явная схема, имеющая точность O(t).
Этот вариант схемы практически непригоден для расчета жестких задач. При a
= 0,5 получается известная схема «с полусуммой». Она имеет точность O(t2)
и безусловно устойчива. При a = 1 имеем неявный метод Эйлера.
Помимо безусловной устойчивости он имеет хорошее качественное поведение
численного решения (за счет L1-устойчивости).
Однако неявный метод Эйлера имеет невысокую точность O(t),
что препятствует его применению.
– решение на новом
временном слое, a – числовой параметр, определяющий
свойства схемы. При a = 0 это явная схема, имеющая точность O(t).
Этот вариант схемы практически непригоден для расчета жестких задач. При a
= 0,5 получается известная схема «с полусуммой». Она имеет точность O(t2)
и безусловно устойчива. При a = 1 имеем неявный метод Эйлера.
Помимо безусловной устойчивости он имеет хорошее качественное поведение
численного решения (за счет L1-устойчивости).
Однако неявный метод Эйлера имеет невысокую точность O(t),
что препятствует его применению.
Описанные выше схемы
вещественны. Однако существует одна комплексная схема этого семейства с ![]() , которая обладает уникальными свойствами
[18]: точность O(t2),
L2-устойчивость и, соответственно,
безусловная устойчивость. Эта схема обладает высокой надежностью и пригодна для
расчетов с сильной жесткостью. В литературе ее принято называть одностадийной
схемой Розенброка с комплексным коэффициентом (CROS).
, которая обладает уникальными свойствами
[18]: точность O(t2),
L2-устойчивость и, соответственно,
безусловная устойчивость. Эта схема обладает высокой надежностью и пригодна для
расчетов с сильной жесткостью. В литературе ее принято называть одностадийной
схемой Розенброка с комплексным коэффициентом (CROS).
Качественно поведение одностадийной схемы Розенброка с комплексным коэффициентом можно описать следующим образом. Для дифференциальной подсистемы делается один шаг точности O(t2), а для алгебраической – одна ньютоновская итерация. Для получения точности O(t2) на дифференциальной подсистеме в правой части (14) необходимо использовать момент t + 0,5t. Однако если использовать этот момент в алгебраической подсистеме, то ньютоновские итерации сходятся именно к этому моменту, а не к нужному значению t + t. Поэтому для алгебраической подсистемы необходимо использовать в правой части (14) момент t + t, что обеспечивает общий второй порядок точности.
Выбор шага интегрирования является важной задачей. С одной стороны, шаг должен быть достаточно малым для того, чтобы обеспечивать заданную точность вычислений; с другой стороны – достаточно большим, чтобы избежать бесполезной вычислительной работы. Традиционным является метод уменьшения шага вдвое, который использовал еще Рунге в своих пионерских работах. Пусть u2 результат последовательного расчета двух шагов t, w – результат расчета одного большого шага 2t. Тогда норма погрешности err оценивается по формуле Ричардсона [18,19]
|
|
(18) |
Затем величина нормы погрешности
сравнивается с заданной величиной допустимой погрешности tol,
что позволяет вычислить оптимальный шаг как 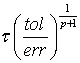 . На
практике, однако данное выражение обычно помножают на «гарантийный фактор» fac
< 1 для предотвращения резких изменений шага интегрирования. В данной работе
. На
практике, однако данное выражение обычно помножают на «гарантийный фактор» fac
< 1 для предотвращения резких изменений шага интегрирования. В данной работе
![]() и
выражение для нового шага интегрирования
и
выражение для нового шага интегрирования
|
|
(19) |
Таким образом, если err < tol, два вычисленных шага считаются принятыми, и решение продолжается исходя из u2. В противном случае оба шага отбрасываются, и вычисления повторяются с шагом tnew.
3.4. Использование параллельных вычислений
На основе вышеизложенного подхода написаны компьютерные программы решения системы уравнений переноса носителей заряда в полупроводнике в диффузионно-дрейфовом и квазигидродинамическом приближениях. На начальном этапе вычислительный алгоритм был реализован на центральном процессоре в однопоточном режиме. Анализ его производительности показал, что основное время вычислений тратится на решение системы линейных алгебраических уравнений (17). С ростом числа узлов расчетной сетки N время вычислений увеличивалось пропорционально N3.
Практика моделирования полупроводниковых приборов позволяет выделить следующие причины для применения расчетных сеток с большим числом узлов:
− наличие в современных приборах областей с резким изменением электрофизических параметров материала: гетеропереходов (скачек диэлектрической проницаемости), резких p-n-переходов (скачек уровня легирования) и т.п., приводит к тому, что имеет место скачок напряженности электрического поля, и, как следствие, резкое изменение электростатического потенциала, концентрации электронов и дырок и их средних энергий. Поэтому корректное моделирование переноса носителей заряда в таких областях возможно лишь при уменьшении шага пространственной дискретизации, что приводит к общему увеличению числа узлов расчетной сетки;
− уменьшение топологических норм изготовления активных элементов микросхем до значений менее 1 мкм повлекло за собой усиление взаимовлияния различных областей их топологии, что существенно изменяет и электрические характеристик элементов. Ранее этими эффектами можно было пренебречь без потери точности моделирования, но для корректного моделирования современных элементов необходимы двумерная и даже трехмерная постановки, а значит увеличение числа узлов расчетной сетки;
− внедрение приборов со сложной латеральной топологией, например, полевых транзисторов с V-образной канавкой затвора. В этом случае для построения корректной численной модели используется более сложная и мелкая сетка пространственной дискретизации уравнений, что обеспечивается увеличением числа ее узлов.
Также увеличение предельных рабочих частот полупроводниковых приборов и интегральных схем, обеспечиваемое сокращением размеров их рабочих областей, требует уменьшения временного шага интегрирования системы уравнений переноса носителей заряда при моделировании высокочастотных и переходных процессов.
Все вышеизложенные факторы приводят к увеличению времени расчета статических, высокочастотных и переходных характеристик перспективных полупроводниковых приборов и интегральных схем. Сокращение времени моделирования может быть достигнуто оптимизацией численного алгоритма решения системы дифференциально-алгебраических уравнений (13), применением высокопроизводительных ЭВМ и распараллеливанием вычислений, прежде всего, операций линейной алгебры.
В течение многих лет одним из основных методом повышения производительности персональных компьютеров и рабочих станций было увеличение тактовой частоты центрального процессора, которая с 1978 г. до 2005 г. возросла с 4,77 МГц (процессор Intel 8086) до 3,8 ГГц (процессор Intel Pentium 4), то есть примерно в 1000 раз. Однако из-за фундаментальных физических ограничений (рост потребляемой мощности и тепловыделения, быстро приближающийся физический предел размера транзистора) в последние годы производители центральных процессоров оказались перед необходимостью поиска замены этому традиционному источнику быстродействия.
В 2005 г. ведущие производители центральных процессоров стали предлагать процессоры с двумя вычислительными ядрами вместо одного. До этого времени только мощные серверы и суперкомпьютеры использовали многопроцессорные и многоядерные вычислительные архитектуры. В последующие годы тенденция увеличения числа ядер центрального процессора закрепилась и в настоящее время на рынке персональных компьютеров представлены 2-, 4- и 6-ядерные процессорные системы. В будущем число ядер центрального процессора будет только возрастать. Программная реализация вычислений на многоядерных и многопроцессорных архитектурах реализуется на основе протокола MPI (Message Passing Interface).
В отличие от центральных процессоров графические процессоры были изначально ориентированы на параллельные вычисления, что обусловлено особенностями обработки графической информации при выводе ее на дисплей. Однако специфическая модель программирования через графические программные интерфейсы OpenGL и DirectX была слишком ограничивающей для большинства разработчиков приложений для научных расчетов.
В ноябре 2006 г. корпорация NVidia выпустила первую видеокарту GeForce 8800 GTX с поддержкой технологии CUDA. В отличие от предыдущих поколений графических процессоров, в которых вычислительные ресурс подразделялись на вершинные и пиксельные шейдеры, в архитектуру CUDA включен унифицированный шейдерный конвейер, позволяющей программе, выполняющей вычисления общего назначения, задействовать любое арифметически-логическое устройство, входящее в состав графического процессора. Так как планировалось, что новое семейство графических процессоров будет использоваться для вычислений общего назначения, то арифметически-логические устройства были сконструированы с учетом требований стандарта IEEE к арифметическим операциям над числами с плавающей точкой одинарной (а позднее и двойной) точности и разработан набор команд, ориентированный на вычисления общего назначения, а не только на графику. Также исполняющим устройствам графических процессоров был разрешен произвольный доступ к памяти для чтения и записи, а также доступ к программно-управляемой кеш-памяти.
Для облегчения доступа разработчиков программного обеспечения к ресурсам технологии CUDA в 2007 г. корпорация NVidia выпустила компилятор расширенной версии языка C/C++, получивший название CUDA C. Несколько позднее был выпущен компилятор CUDA Fortran.
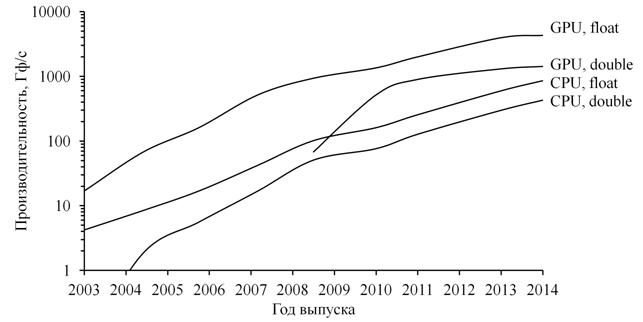
Сравнение роста производительности графических и центральных процессоров представлено на рисунке 1. В настоящее время производительность «настольных суперкомпьютеров» на базе специализированных графических карт Tesla K40 корпорации NVidia достигла 4,3 Тф/с [15].
Максимальное ускорение, которое можно получить от распараллеливания программы, дается законом Амдала [12]
|
|
(20) |
где P – доля вычислений, которая может быть идеально распараллелена на N независимых потоков (нитей).
|
|
|
Рисунок 1. Сравнение роста производительности графических и центральных процессоров за последнее десятилетие: GPU, float – графический процессор одинарная точность, GPU, double – графический процессор двойная точность, CPU, float – центральный процессор одинарная точность, CPU, double – центральный процессор двойная точность [12-15, 22] |
Таким образом, учитывая данные, приведенные на рисунке 1, выражение (20), то обстоятельство, что число физических ядер современных графических процессоров в разы превосходит количество ядер центральных процессоров, а скорость переключения между выполняемыми нитями на графическим процессоре на порядки превосходит аналогичный показатель для центральных процессоров, задача распараллеливания вычислений с применением графических процессоров для научных и инженерных расчетов является актуальной.
4. Результаты моделирования
4.1. Решение уравнения Пуассона с применением технологии CUDA массивно-параллельных вычислений
На предварительном этапе для оценки эффективности распараллеливания вычислений и погрешности расчетов отдельно решалось двумерное уравнение Пуассона. Решение данной задачи также имеет самостоятельное значение, так как уравнение Пуассона описывает распределение потенциала электрического поля в задачах электростатики и стационарное распределение температуры, например, в изделиях микроэлектроники.
В качестве тестовой задачи рассматривалось уравнение
|
|
(21) |
в области x, y Î [0, 1] с периодическими граничными условиями, имеющее точное решение
|
|
(22) |
|
|
|
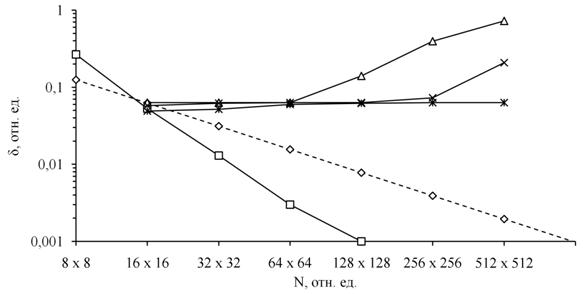
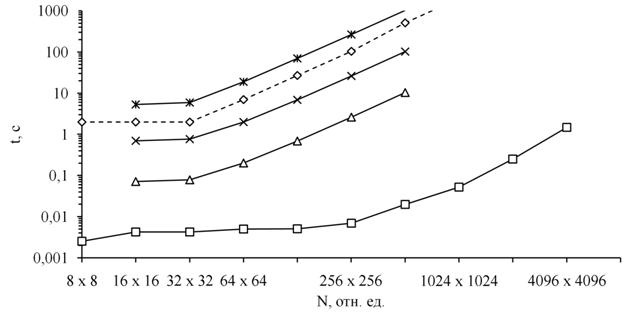
Рисунок 2. Зависимость погрешности численного решения тестовой задачи от числа узлов расчетной сетки: ◊ – оценка погрешности 1/N, □ – метод преобразования Фурье, ∆ – метод простой итерации (2000 итераций), × – метод простой итерации (20000 итераций), ж – метод простой итерации (200000 итераций) |
На рисунке 2 приведена зависимость погрешности численного решения тестовой задачи (21) в сравнении с точным решением по формуле (22) от числа узлов расчетной сетки для различных алгоритмов. Видно, что увеличение числа узлов расчетной сетки уменьшает погрешность решения уравнения Пуассона при применении алгоритма быстрого преобразования Фурье. Погрешность численного расчета решения задачи (21) методом простой итерации зависит от числа узлов расчетной сетки и количества итераций. При заданном числе узлов имеет место снижение погрешности до некоторой константы с ростом числа итераций. Общей закономерностью является требование увеличения числа итераций для обеспечения заданной точности решения с ростом числа узлов расчетной сетки, что объясняется ухудшением обусловленности матрицы.
|
|
|
Рисунок 3. Зависимость времени решения тестовой задачи от числа узлов расчетной сетки: ◊ – расчет методом простой итерации на центральном процессоре (20000 итераций), □ – метод преобразования Фурье, ∆ – метод простой итерации (2000 итераций), × – метод простой итерации (20000 итераций), ж – метод простой итерации (200000 итераций)
|
На рисунке 3 приведена зависимость времени решения задачи (21) от числа узлов расчетной сетки для различных алгоритмов. Видно, что применение быстрого преобразования Фурье для решения уравнения Пуассона позволяет резко снизить время вычисления по сравнению с более общим итерационным алгоритмом. К сожалению, метод решения уравнения Пуассона на основе быстрого преобразования Фурье накладывает жесткие ограничения на граничные условия задачи, которые должны быть нулевыми или периодическими, что сужает применимость данного алгоритма. В целом увеличение производительности при решении уравнения Пуассона на графической карте составляет около 10 раз. Для тестирования использовалась система Intel® Core™ 2 Duo CPU T6500 @ 2.1 GHz GeForce GT 120M 1.25 GHz.
4.2. Решение системы уравнений переноса носителей заряда в полупроводниковых приборах с применением технологии CUDA массивно-параллельных вычислений
Для исследования возможностей повышения производительности вычислений при применении технологии CUDA программы решения системы уравнений переноса носителей заряда в полупроводниковых приборах в диффузионно-дрейфовом и квазигидродинамическом приближениях были модернизированы. Наиболее вычислительно емкая процедура решения системы линейных алгебраических уравнений на каждом шаге интегрирования системы дифференциально-алгебраических уравнений была перенесена на графический процессор.
Характерными особенностями матрицы Якоби системы дифференциально-алгебраических уравнений, полученной из системы дифференциальных уравнений в частных производных являются большая размерность и разреженность. Это обусловливает применение итерационных методов для решения системы линейных алгебраических уравнений такого рода задач, например метода бисопряженных градиентов (BiCG). Так как изначально версия программы, целиком выполняемая на центральном процессоре, использовала LU-разложение для решения системы линейных алгебраических уравнений, для корректного сравнения была разработана программа, целиком выполняемая на центральном процессоре и использующая метод бисопряженных градиентов для решения системы линейных алгебраических уравнений. Таким образом, в тестировании участвовали три версии программы (таблица 3).
Таблица 3. Описание тестируемых программ
|
Номер версии |
Метод решения системы линейных алгебраических уравнений |
Используемый для расчетов процессор |
|
1 |
исключения Гаусса (LU-разложение) |
центральный |
|
2 |
бисопряженных градиентов |
центральный |
|
3 |
бисопряженных градиентов |
графический |
Тестирование программ проводилось на двух персональных компьютерах с различной производительностью, основные характеристики которых представлены в таблице 4.
Таблица 4. Характеристики персональных компьютеров, используемых для тестирования программ
|
Номер ПК |
Характеристики центрального процессора (ЦП) и оперативной памяти (ОЗУ) |
Характеристики видеокарты |
|
1 |
Intel Core 2 Duo, 2.8 ГГц, 2.8 ГГц ОЗУ – 2 Гб |
NVidia GeForce 9500 GT |
|
2* |
Intel Core i7-2600, 3.4 ГГц, 3.7 ГГц ОЗУ – 8 Гб |
NVidia GeForce GTX 560 |
* Производительность центрального и графического процессоров выше
В качестве объекта моделирования была рассмотрена кремниевая диодная структура из работы [8] с топологией p-области: Na = 1016 см-3, Lp = 50 мкм; n-области: Nd = 1016 см-3, Ln = 50 мкм и электрофизическими параметрами кремния: m0n = 1440 см2/(В×с), tn = 10‑7 c, m0p = 480 см2/(В×с), tp = 10‑7 c. Коэффициенты Оже-рекомбинации предполагали равными Cn = 1,1×10-30 см6/с и Cp = 0,3×10-30 см6/с.
4.2.1. Исследование стационарного решения
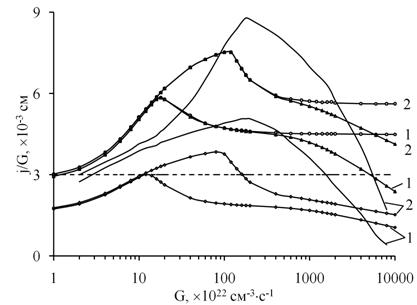
Результаты моделирования воздействия стационарного ионизирующего излучения на тестовую диодную структуру, приведенные на рисунке 4, сравнивали с данными работы [8]. Качественный ход полученных зависимостей ионизационного тока от темпа генерации неравновесных носителей заряда совпадает с литературными данными. Имеющие место отличия результатов объясняются большим числом узлов расчетной сетки (N = 8…1024 в данной работе против N = 70 в работе [8]) и меньшей нормой невязки, при которой решение считалось достигнутым (δ = 10-7 в данной работе против δ = 10-2 в работе [8]).
|
|
|
Рисунок 4. Зависимость отношения нормированного на темп генерации плотности тока к темпу генерации электронно-дырочных пар от темпа генерации электронно-дырочных пар: 1 – U = 0 В, 2 – U = -5 В; - - - – аналитическая модель [8];
|
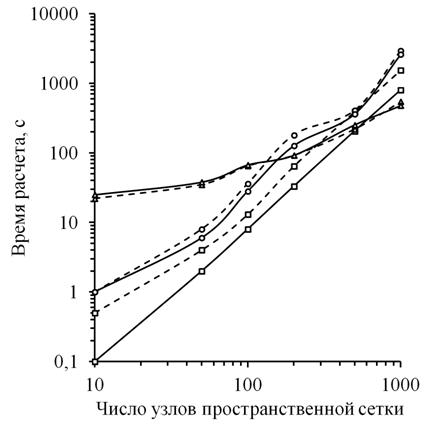
Задача решалась методом установления. Характерные времена решения в зависимости от числа узлов расчетной сетки приведены на рисунке 5.
Из результатов, приведенных на рисунке 5, видно следующее:
− заметное сокращение времени расчета от применения распараллеливания вычислений на графическом процессоре при решении рассматриваемой нами тестовой задачи наблюдается при N > 512;
− с увеличением числа узлов пространственной сетки (при N > 512) прирост времени выполнения программы, полностью выполняемой на центральном процессоре, значительно больше, чем для программы, часть операций которой выполняется на графическом процессоре, независимо от метода решения системы линейных алгебраических уравнений (прямого или итерационного);
− обработка данных на графических процессорах с одинарной точностью не приводит к их заметному искажению по сравнению с обработкой на центральных процессорах с двойной точностью.
|
|
|
Рисунок 5. Зависимость времени расчета при решении тестовой задачи от числа узлов пространственной сетки для трех версий программы и двух персональных компьютеров с различной производительностью: (- - -) – персональный компьютер 1; (—) – персональный компьютер 2; □ – версия программы 1; ○ – версия программы 2; ∆ – версия программы 3 |
4.2.2. Исследование переходных процессов
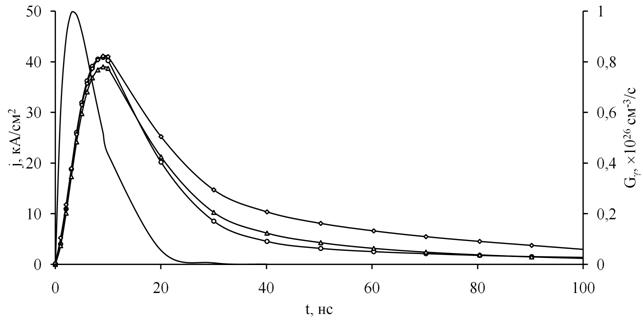
Результаты моделирования воздействия биэкспоненциального импульса ионизирующего излучения при различных температурах кристаллической решетки полупроводника приведены на рисунке 6. При проведении расчетов учитывали температурные зависимости концентрации собственных носителей заряда в полупроводнике и подвижностей электронов и дырок.
Характерный временной шаг интегрирования системы дифференциально-алгебраических уравнений составил порядка 10-13 с на фронте импульса излучения с последующим увеличением до единиц наносекунд на его спаде. Аналогичный расчет на основе явной численной схемы с большей погрешностью требует временного шага интегрирования порядка 10-15 с. Отметим, что с уменьшением длительности фронта импульса ионизирующего излучения, например, при рассмотрении воздействия лазерного импульса наносекундной длительности, эффективность одностадийной схемы Розенброка с комплексным коэффициентом будет только возрастать.
|
|
|
|
Из графика видно, что увеличение температуры кристаллической решетки тестовой диодной структуры с 300 К до 700 К практически не меняет максимальное значение плотности мгновенной составляющей ионизационного тока, величина которого определяется максимальной интенсивностью излучения. Однако с ростом температуры увеличивается вклад запаздывающей компоненты ионизационного тока, приводящей, в конечном счете, к развитию радиационно-стимулированного лавинно-теплового пробоя. Данный процесс теоретически и экспериментально исследован в работе [23].
Заключение
Сфера применения параллельных вычислений, в частности на графических процессорах, в вычислительной физике неуклонно расширяется. Это позволяет решать как уже существующие задачи с большей детализацией, так и ставить принципиально новые вычислительно сложные задачи. Представленная в данной работе одномерная квазигидродинамическая модель переноса носителей заряда в полупроводниковых приборах легко может быть обобщена на двумерный и трехмерный случай. При этом, по-видимому, более эффективной будет являться пространственная дискретизация методом конечных объемов, обладающая свойством естественной консервативности. Отметим, что расширение математической модели (введение новых уравнений, увеличение размерности задачи) не требует изменения постановки и решения системы дифференциально-алгебраических уравнений, а рост числа узлов расчетной сетки только увеличит эффективность параллельного алгоритма.
Результаты работы доложены на Первой Российско-белорусской научно-технической конференции «Элементная база отечественной радиоэлектроники», посвящённой 110-летию со дня рождения О. В. Лосева, Нижний Новгород, 11-14 сентября 2013 г.
Литература
1. Ricketts L.W. Fundamentals of Nuclear Hardening of Electronic Equipment. – Wiley-Interscience, 1972. – 548 P.
2. Коршунов Ф.П., Гатальский Г.В., Иванов Г.М. Радиационные эффекты в полупроводниковых приборах. – М.: Наука и техника, 1978. – 232 с.
3. Gwyn C.W., Scharfetter D.L., Wirth G.L. The analysis of radiation effects in semiconductor junction devices // IEEE Transactions on nuclear science. 1967. V.NS-14, №6. P.153-159.
4. Gummel H.K. A self-consistent iterative scheme for one-dimentional steady – state transistor calculation // IEEE Transactions on electron devices. 1964. V.ED-11. P.455-465.
5. Sandborn P.A., Rao A., Blakey P.A. An assessment of approximate nonstationary charge transport models used for GaAs device modeling // IEEE Transactions on electron devices. 1989. Vol.ED-36, №7. P.1244-1253.
6. Demarina N.V., Obolensky S.V. Modeling of ionizing irradiation influence on Schottky-gate field-effect transistor // Microelectronics Reliability. 1999. Vol.39. P.1247-1263.
7. Оболенский С.В. Предел применимости локально-полевого и квазигидродинамического приближений при расчетно-экспериментальной оценке радиационной стойкости субмикронных полупроводниковых приборов // Известия ВУЗов. Электроника. 2002. №6. С.31-38.
8. Кудряшов Н.А., Кучеренко С.С., Сыцько Ю.И. Математическое моделирование фотоэлектрических процессов в полупроводниковых элементах при высоком уровне фотовозбуждения // Математическое моделирование. 1989. Т.1, №12. С.1-12.
9. Gear C.W. Numerical Initial Value Problems in Ordinary Differential Equations. – Englewood, New Jersey: Prentice Hall, 1971. – 253 P.
10. Валиев К.А., Вьюрков В.В., Орликовский А.А. Кремниевая наноэлектроника: проблемы и перспективы // Успехи современной радиоэлектроники. 2010. №6. С.7-22.
11. Lundstrom M. Fundamentals of carrier transport. – Cambridge University Press, 2000. – 418 P.
12. Боресков А.В., Харламов А.А. Основы работы с технологией CUDA. – М.: ДМК Пресс, 2010. – 232 с.
13. Сандерс Д., Кэндрот Э. Технология CUDA в примерах: введение в программирование графических процессоров. – М.: ДМК Пресс, 2011. – 232 с.
14. Боресков А.В., Харламов А.А., Марковский А.А., Микушин Д.Н., Мортиков Е.В., Мыльцев А.А., Сахарных Н.А., Фролов В.А. Параллельные вычисления на GPU. Архитектура и программная модель CUDA. – М.: МГУ, 2012. – 336 с.
15. Электронный ресурс http://www.nvidia.com
16. Scharfetter D.L., Gummel H.K. Large-signal analysis of silicon Read diode oscillator // IEEE Transactions on electron devices. 1969. Vol.ED-16, №1. P.64-77.
17. Ting Wei Tang Extension of the Scharfetter-Gummel algorithm to the energy balance equation // IEEE Transactions on electron devices. 1984. Vol.ED-31, №.12. P.1912-1914.
18. Альшин А.Б., Альшина Е.А., Калиткин Н.Н., Корягина А.Б. Схемы Розенброка с комплексными коэффициентами для жестких и дифференциально-алгебраических систем // Журнал вычислительной математики и математической физики. 2006. Т.46, №8. С.1392-1414.
19. Хайрер Э., Ваннер Г. Решение обыкновенных дифференциальных уравнений. Жесткие и дифференциально-алгебраические задачи. М.: Мир, 1999. – 685 с.
20. Электронный ресурс http://www.synopsys.com
21. Rosenbrock H.H. Some general implicit processes for the numerical solution of differential equations // Comput. J. 1963. V.5, №4. P.329-330.
22. Электронный ресурс http://www.intel.com
23. Пузанов А.С. Перенос электронов в транзисторных структурах в сильных резконеоднородных электрических полях при воздействии потока квантов высоких энергий // Диссертационная работа на соискание ученой степени кандидата физико-математических наук. – Н.Новгород, 2011. – 162 с.