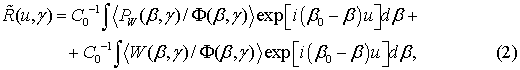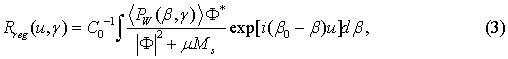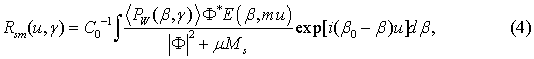|
"JOURNAL OF RADIO ELECTRONICS" N 6, 2007 |
SUPER RESOLUTION IN THE WAVEGUIDE INVERSE LIGHT SCATTERING PROBLEM
A. A. Egorov
Peoples’ Friendship University of Russia, Moscow, RussiaReceived May 27, 2007
A new method of studying with super resolution the waveguide irregularities on the basis of the waveguide light scattering in the presence of noise is presented.
1. Introduction
The light scattered in an irregular waveguide can be registered as radiated substrate-cover (substrate-air) and substrate modes, and as the radiation, scattered in the plane of a waveguide [1-6]. When there is a need to obtain information about the statistic characteristics of the waveguide irregularities, the main task consists in correct solution of the direct and inverse scattering problems [1-5].
Note that the mathematical physics differs between well- and ill-posed problems [7,8]. The problem is well-posed if the following conditions are satisfied: (a) solution exists; (b) solution is single-valued; (c) solution continuously depends on the input data (i.e., small variations in the input data lead to small variations in the solution), which means that the solution is stable. The problems that do not comply with these conditions are ill-posed problems. The inverse problems of the theory of scattering are classified in mathematical physics as ill-posed problems. Linear inverse problems can be solved using the method of comparison, the Tikhonov trial-and-error method, the Ivanov quasi-solution method, the Backus-Gilbert method, the Tikhonov regularization method, etc. [7,8].
We propose an approach based on a combination of classical regularization [7,8] and quasi-optimal smoothing [1-4]. The essence of the method is as follows: the scattering noisy diagram is measured by a point photo detector in the far-field zone, and then the digitized intensity values are processed according to the procedure described briefly below.
2. 2D-inverse waveguide light scattering problem in the presence of noise
The 2D-problem of waveguide far-field zone scattering is formulated using next equation
In the equation (1): A is a linear integrated operator with a kernel Φ; β is the longitudinal component of a propagation constant of radiating modes; F is the spectral density function (SDF) of the statistical irregularities i.e. the function on which is solved the inverse problem; PW = P + W; P is the power scattered in the waveguide, W is the intensity of the statistic additive real noise given in the interval of the observable radiating modes; γ is the effective refraction index; < … > means averaging on an ergodic ensemble of statistically identical systems. The kernel Φ is the so-called waveguide optical factor (some waveguide optical transfer function). The linearity of the problem is understood in a sense of the linear dependence of P on F. The main steps of the solution of the delivered two-dimensional problem of waveguide light scattering on statistical waveguide irregularities explicitly are considered in our papers [1-4].
In a case of differential waveguide light scattering in the presence of noise the restoration of the autocorrelation function (ACF is the Fourier-transform of SDF)
is performed via the formula
The nature of noise in experiments has been analyzed in our papers [3, 4]. Here, we should note that the scattering light pattern PW is taken at the fixed instants t (e.g., by the CCD), and then one can use the averaging over the ergodic ensemble. Therefore we omit the time dependence.
Scattered power PW is measured in the far-field (Fraunhofer) zone or in the equivalent Fourier plane at a certain bounded interval (for example (-β1, +β1)) of the real propagation constants β of the radiating modes (see Fig.1).
Diagram of the propagation constants β of the guided modes and radiative modes an asymmetric integrated-optical waveguide illustrating the scattering of laser radiation by waveguide irregularities is presented in Fig. 1. In the Fig. 1: β1 = kn1, β2 = kn2, β3 = kn3, and β0 = kγ, where n1, n2, and n3 are the refractive indices of air (surrounding medium), the waveguide layer, and substrate, respectively (n2 > n3 > n1); γ is the effective waveguide refractive coefficient; and
is a complex vector of the propagation constant of the radiative modes with components
and
;
is the SDF estimation obtained from
; θ is the scattering angle.
Fig. 1. Diagram of the propagation constants β of the guided and radiative modes of an asymmetric integrated-optical waveguide.
Next to the estimation
the classic regularization method [7] is applied according to the formula
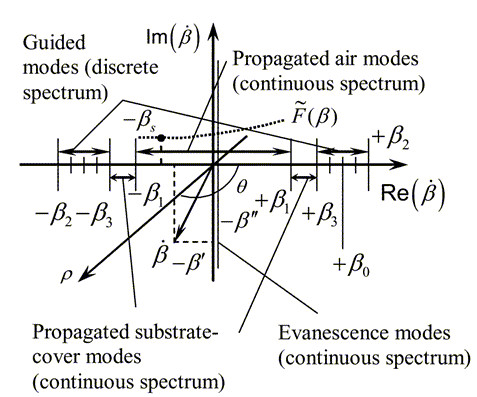
where u = z - z', z and z' are coordinates in the plane of object, i.e. the waveguide irregularities; β0 = kγ is the propagation constant of the waveguide mode; k = 2π/λ, λ is the laser radiation wavelength; Ф* is the complex conjugate to Ф; μ is the regularization parameter; the elementary stabilizers of p-order are taken as M1 = β2p or M2 = (β0 - β)2p, p ≥ 0 is the regularization order.
The limited extrapolation of the restored spectral density function of roughness beyond the limits of the range of wave numbers of the observable radiating substrate-air and substrate modes in the presence of the given noise has not allowed solving completely the delivered problem: the error of restoration remained large. In this connection the procedure of a quasi-optimal regularization [1-4] is applied for deriving an approximate correct solution of the inverse waveguide scattering problem
where E is a smoothing function, permitting to synthesize linear filter that weighs the values of the noisy scattering pattern at the sampling points; non-fixed (variable) interval mu < L, L is the length of the irregular region.
Application of the classic regularization method to a modeling solution of the posed inverse problem of the waveguide light scattering is depicted in Fig. 2. TE0-mode is propagated in the given irregular symmetric waveguide with refraction index of the waveguide layers: n1 = n3 = 1.46 (quartz plates), n2 = 1.59 for the light wavelength λ = 0.63 μm (He-Ne laser). Geometric parameters of the quartz substrate surface roughness: σ = 5 nm and r = 30 nm. The waveguide effective refraction index γ = (1) 1.479, (2) 1.525, (3) 1.556, (4) 1.571. Specific (curve 5) Gaussian autocorrelation function R(u) and restored (curves 1-4) ACFs Rreg(u, γ) in arbitrary units are presented in Fig. 2. One can see that specific Gaussian ACF is restored with a large error (in the metric L2 the error of restoring is about 150%).
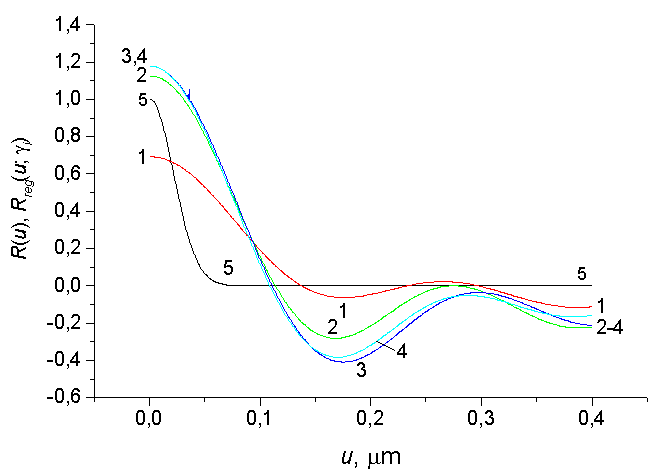
Fig. 2. ACFs Rreg(u, γ) restored via Eq.(3). Parameters of the problem: μ = 0.5, p = 0.6. There is no noise.
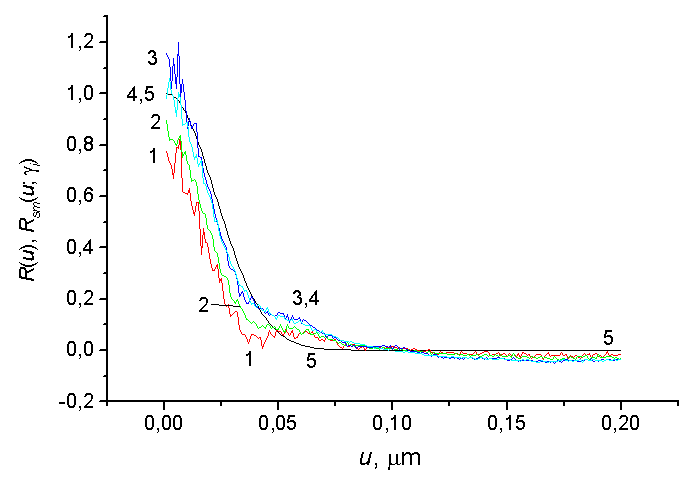
To illustrate the possibilities of the quasi-optimal regularization with the use of the sampling theorem the follow-on of restoring the ACF Rsm(u, γ) are presented in Fig. 3. The error of restoring the initial Gaussian ACF R(u) does not exceed 27% and can be reduced by selection, both other smoothing function, and parameters of the solution of the waveguide inverse scattering problem. Our method permits achieving the certain super resolution on the correlation radiuses: the initial correlation radius is determined here with an error not grater than 7% (40 times less than for Fig. 2).
Fig. 3. ACFs Rsm(u, γ) restored via Eq.(4). Parameters of the problem: μ = 1, p = 0.8, m = 12 (for the function E like sinmx/mx). <S/N> = 7. Remaining parameters are as for Fig. 2.
The smoothing function E is selected from the condition of the minimum rms error of reconstructing of the specified ACF R(u)
Then we can consider the following expression (6) as the rms error of approximation of the initial continuous SDF
with the help of functions of limited length
. The minimum error, accessible for this approximation is equal to
(6)
This error is equal to the “energy” containing mainly in the high-frequency part of the spectrum of the surface roughness “power”
, that is in the range of values
. In the equation Eq. (6)
determines boundary frequency, after which the optical waveguide factor Φ is equal to zero. From the view of the optimum filtration theory the formula Eq. (4) allows to attenuate primarily the high frequency noise components.
Conclusion
Integrated-optical waveguides serve as a basis for creation of various integrated optical circuits. In this connection, an important direction in current technology is the development of methods for creating integrated-optical waveguides with a very low level of losses on scattering on the waveguides irregularities.
As a rule, when analyzing light scattering, main attention is given to solving the direct scattering problem (determination of the characteristics of the field or intensity of the radiation scattered in a waveguide). The scattering diagrams are then used to solve an inverse problem by a known comparison method, when one tries to achieve coincidence, for example, by the least squares method, between the experimentally measured diagrams and calculated theoretically.
In the presented new method we search for an approximate correct solution of the posed inverse problem in the class of functions that are integrable with respect to the square of modulus L2. The uniqueness of this solution is interpreted as the uniqueness of the solution that is statistically averaged with respect to an ensemble or averaged with respect to a single relatively long realization. The stability of the solution is reached with a restriction of the set of solutions to a compact set representing a set of functions depending on a finite number of parameters.
References
1. Egorov A.A. Correct investigation of the statistic irregularities of integrated optical waveguides with the use of the waveguide light scattering, Las. Phys. Lett., 1, pp. 421-428 (2004).
2. Egorov A.A. Inverse problem of laser light scattering in an integrated optical waveguide: 2D solution with accurate input data, Las. Phys., 14, pp. 1296–1309 (2004).
3. Egorov A.A. Reconstruction of the experimental autocorrelation function and determination of the parameters of the statistical roughness of a surface from laser radiation scattering in an integrated-optical waveguide, Quantum Electronics, 33, pp. 335–341 (2003).
4. Egorov A.A. Use of waveguide light scattering for precision measurements of the statistical parameters of irregularities of integrated optical waveguide materials, Opt. Eng., 44, pp. 014601-1–014601-10 (2005).
5. Marcuse D. Light Transmission Optics. – New York: Van Nostrand, 1972.
6. Hunsperger R.G. Integrated Optics: Theory and Technology. – New York: Springer-Verlag, 1984.
7. Tikhonov A.N. and Arsenin V.Ya. Solutions of Ill-Posed Problems. 3rd ed. – New York: Halsted, 1977.
8. Colton D. and Kress R. Integral Equation Methods in Scattering Theory. – New York: Wiley, 1984.
Author Information
Alexandre Alekseyevich Egorov is a professor at Peoples Friendship University of Russia (PFUR). He received his PhD and Dr.Sc. degrees in physics and mathematics in 1992 and 2006, respectively. Since 1984 he has been with PFUR as junior research fellow, research fellow, and senior research fellow. In 1992 he became an associate professor and in 2006 he became a professor. He has carried out research in integrated optics, thin film optics, laser physics, optical processing, computer modeling, physical ecology and heterodyne differential microscopy-profilometry. Since 1993 he has also been a senior research fellow with the General Physics Institute of Russian Academy of Sciences. He has published more than 130 scientific and technical papers. His main interests are laser physics, integrated optics, statistical optics, heterodyne microscopy-profilometry, physical ecology, and computer modeling. He is a member of the Presidium and a member of the Board of Moscow A.S. Popov Scientific, Technical, Radio-techniques, Electronics and Communication Society.