| "JOURNAL OF RADIOELECTRONICS" N 10, 2000 |
A PROPOSED EXPERIMENT OF DIRECT DETECTING OF THE VECTOR POTENTIAL WITHIN CLASSICAL ELECTRODYNAMICS
V.
Onoochin
"Sirius", 3A Nikoloyamski lane, Moscow 109004, , Russia
An experiment within the framework of classical electrodynamics is proposed, to demonstrate Boyer’s suggestion of a change in the velocity of a charged particle as it passes close to a solenoid. The moving charge is replaced by an ultra-short pulse (USP), whose characteristics should depend on the current in the coil. This dependence results from the exchange of energy between the electromagnetic field of the pulse and the magnetic field within the solenoid. This energy exchange could only be explained by assuming that the vector potential of the solenoid has a direct influence on the pulse.
PACS 41.10
1. Introduction.
It has been assumed for some time that electromagnetism is completely described by electromagnetic fields. Potentials, especially in classical electrodynamics, are treated as merely a convenient mathematical tool for calculations concerning these fields. However, Aharonov and Bohm (A-B) have shown that in the quantum description potentials rather than fields play the essential role [1]. Unfortunately, the requirements placed on experiments which might determine the existence of the AB effect are so stringent that other interpretation of the obtained results are possible. The Aharonov-Bohm interpretation has therefore been questioned [2, 3].
We are able now to describe an experiment to detect the vector potential directly, whithin classical electrodynamics. The essential advantage of this experiment is that it requires less accuracy in the measurements of the currents and fields. The concept of the experiment originated in the work of Boyer [4] which predicts a change to the velocity of the particle as it passes near the solenoid:

Here, p and q are the particle momentum and charge. According to this model, the particle slows when approaching the solenoid and then speeds up when leaving. Below we point out such a possibility (we follow the consideration presented in Ref.5).
The total energy W of the system, considering both the solenoid and the charged particle, is
where Bs is the fixed magnetic field due to a current in the solenoid, Bp is the magnetic field due to the motion of the charged particle, and m and v are mass and velocity of that particle, respectively. There may be additional terms involving the source of the current, but they do not change the argument.
Since the Bs2 term is fixed, the sum of the other terms should be constant. For constant particle velocity v, both the kinetic energy term and the Bp2 term would be constant. However, the BsBp term is certainly not constant as the particle approaches and then recedes from the solenoid. Therefore the velocity cannot be constant.
The aim of this paper is to describe an experimental method of demonstrating the above within the framework of classical electrodynamics. It should be noted that the charge is not needed to show its velocity change, it may be replaced by a current qv. Therefore, in the real experiment, it is proposed to use a single ultrashort pulse (USP) to acts as this current.
The experiment is described in Section 2. In Sec. 3 we point out some electromagnetic properties of the USP which allow to achieve expected result. In Sec.4 we calculate the energies of the fields and currents involved in the process, giving the expression for the interaction that can influence the characteristics of the USP. Finally, in Sec.5 we discuss the possible results of the experiment in both cases, firstly in the situation when the characteristics are assumed to change, and secondly when they are assumed not to do so.
2. Design of experiment.
The arrangement of the proposed experiment is shown in Fig.1 (top view). Two wires form a dipole antenna. The antenna is placed in an anechioc chamber, in order that only the original signal will be observed by the spectrometer used to observe signals from different parts of antenna. The diameter of the wires is chosen simply to suit the requirements of mechanical rigitily; 1m wires can be fixed only at the point where the coaxial cable from the pulse generator connect to the dipole, and must remain straight.
Two solenoids (noted by the letters s in Fig.1) are placed in the chamber. These are designed to be equivalent to those used for the A-B experiments, i.e. the pulses in the wires can be influenced only by the vector potential of the solenoid, but not by its magnetic field. Because if the solenoid is formed of the cylindrical coil it always exists some “leakage” of the magnetic field through the insulation layer of the wires independently of how close the adjacent turns of the coil are mounted each to the other. So actually some nonzero magnetic field created by the current in the coil does exist outside the solenoid. To eliminate this factor, it is possible to use the solenoid formed of the cylinder made of soft magnetic materials. Using of such soft materials allows to control the magnitude of the magnetic momentum inside the solenoid, and at the same time, there will be no magnetic field outside the cylinder. To eliminate the magnetic field caused by the edge effects, it is possible to use the magnetoguides which form jointly with the solenoids the closed circuit for the magnetic flux.
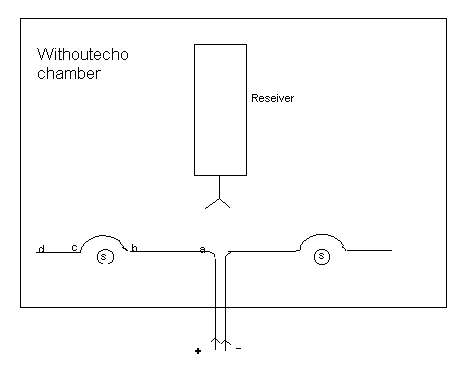
Fig. 1
The USPs from the signal generator pass through the coaxial cable and appear as electromagnetic radiation from the antenna, and the physical form of the wire determines a path of the USP near the solenoid and the radiative losses from the signal. Losses can be significant at bends in the conductors, but if their radius of curvature is much greater than the diameter of the wire, the losses will be small since there is little deceleration of the current at the USP.
The generator can produce USP with duration of order of 10-10 sec., by the way, the repetition time of generation of each separate pulse is of order of 10-5 sec. [6, 7], so we are able to assume the pulses as single ones. The characteristics of the USP are determined after the radiation and after the pulse from the ends of the antenna and returning to the generator. The ideal matching of the antenna is achieved in case of full absence of the reflected pulses under the condition of zero current in both solenoids (in performed experiments with similar design, the magnitude of reflected current pulse typically was higher 95% of the USP loading the wire antenna).
Two solenoids are used to achieve more matching of the wires characteristics, by the way, they are placed under the wires (see Fig. 1) for eliminating the influence of displacement current generated between the wires. So when the USPs pass in dipoles of the antenna this current can influence a radiation region but not the region where the solenoids are placed.
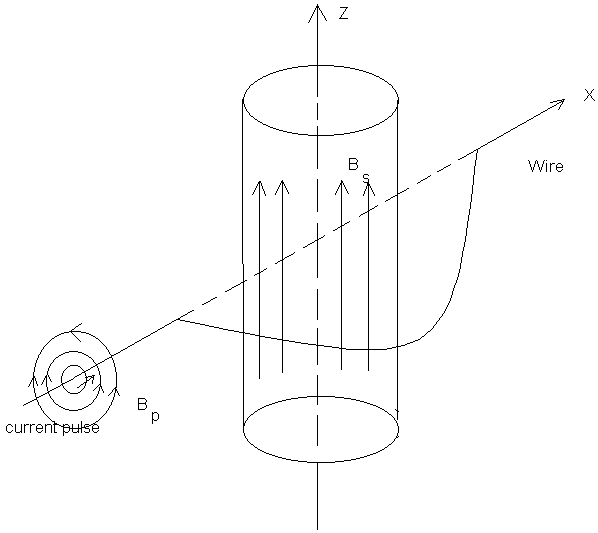
Fig. 2
Each wire has two parts. At the first one (noted as ab), each USP moves transversally to direction of the vector potential created by solenoid (along the x axis, see Fig. 2) so the interaction term between the USP and the solenoid
![]()
should be equal to zero. Here, ![]() is the current density at the USP and A is the
vector potential of the solenoid, Vw is
the volume of the wire at the part ab. At the
second one (bc), the USP moves on arc, i.e. along
direction of the vector potential so the interaction term should achieve a
maximum. We choose a length of arc bc greater than
the length of the USP. Only in this case, whole current of the USP gives a
contribution into the interaction term.
is the current density at the USP and A is the
vector potential of the solenoid, Vw is
the volume of the wire at the part ab. At the
second one (bc), the USP moves on arc, i.e. along
direction of the vector potential so the interaction term should achieve a
maximum. We choose a length of arc bc greater than
the length of the USP. Only in this case, whole current of the USP gives a
contribution into the interaction term.
3. The electromagnetic properties of the USP.
Here, we give more explanation on the EM properties of the
USP because we have seeming contradiction since it is well known that the EM
pulse radiated by the antenna is always of plus and minus polarity. It is caused
by the fact that the radiated field E is
proportional to the time divergence of the current ![]() at the pulse. Therefore, due to plus and minus polarity the total contribution
of
at the pulse. Therefore, due to plus and minus polarity the total contribution
of ![]() to the
interaction term can be equal to zero so we have no expected effect. However,
such a differentiation of
to the
interaction term can be equal to zero so we have no expected effect. However,
such a differentiation of ![]() takes place only at the ends (points d) of the antenna so on the arc bc
each USP still remains of the only one polarity. One can object that when the
reflected USP returns from the ends of the antenna, it has the polarity opposite
to polarity of incoming USP, and because amount of the energy of reflected USP
is about (and more) 95% of the amount of the energy of incoming USP, the total
sum of the interaction term during the time of travelling separate USP through
the wire is quite equal to zero. But we do not intend to measure the energy
characteristics of the USP, we intend to measure changing the parameters of the
radiated signals which are separated in time for incoming and reflected USP, and
we intend to measure the changing the duration of the USP.
takes place only at the ends (points d) of the antenna so on the arc bc
each USP still remains of the only one polarity. One can object that when the
reflected USP returns from the ends of the antenna, it has the polarity opposite
to polarity of incoming USP, and because amount of the energy of reflected USP
is about (and more) 95% of the amount of the energy of incoming USP, the total
sum of the interaction term during the time of travelling separate USP through
the wire is quite equal to zero. But we do not intend to measure the energy
characteristics of the USP, we intend to measure changing the parameters of the
radiated signals which are separated in time for incoming and reflected USP, and
we intend to measure the changing the duration of the USP.
It is accepted that propagation of electromagnetic field inside the metal is described by the following wave equation [8]
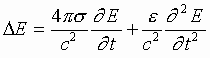
Here, ![]() and
and ![]() are
conductance and dielectric constant of the metal (the material of the wire).
are
conductance and dielectric constant of the metal (the material of the wire).
However, one must note that the above equation is able to describe the transversal components of the EM field only, but the EM field of the UPS is of longitudinal type, i.e. the vector of the electric field is directed along the vector of the current (otherwise, i.e. if the electric field of the USP is of transversal type, the current pulse would radiate the longitudinal EM waves which is impossible). So here we have an example of the longitudinal EM field propagating with the velocity comparable to the speed of the light. To the author’s knowledge, unfortunately, the correct equation describing behavior of the USP is unknown in scientific literature. But we will not need to know the explicit functional dependence of the electric field of the USP on the spatial and time variables.
Thus, the USP moves along the wire and its magnetic field penetrates inside the solenoid. Therefore, according to the Eq.(1) the total energy of the system changes. However, to detect this changing, we face some problems:
The most difficult problem is the the problem of correct describing the penetration of the magnetic field of the USP into the solenoid [9]. To overcome this problem, we use the method presented by the author in Ref. 10, i.e. we assume that the original magnetic field of the USP penetrates into the solenoid without any changing but this magnetic field induces some current i in the coil of the solenoid, the current i creates the additional magnetic field which penetrates into the solenoid too, and the true magnetic field penetrating into the solenoid, except own magnetic field of the solenoid is the algebraic sum of the original and induced magnetic fields.
We should note that we are not able to calculate the additional magnetic field, it is too combersome problem [9] but we are able to avoid such calculations in the following way:
We perform two experiments under quite identical conditions but with the only difference, namely, during the first experiment, the value of the initial current in the coil of the solenoid is I , and during the second experiment, the value of the initial current in the coil of the solenoid is zero.
Because of the principle of superposition in the electrodynamics, value of the current i induced in the coil of the solenoid by the current of the USP does not depend on the value of the initial current in the solenoid, so the value of the current i must be the same in both experiments. Therefore, by substracting the results of the second experiment from the results obtained in the first experiment (experimentally by comparing the results of both experiments one to another), we eliminate all terms, containing the current i, from our calculations. It allows to resolve all problems noted above. We discuss the procedure of substracting the terms with i in more details in the Sec. 4.
4. Calculation of the EM energy of the system.
It should be noted that the exact calculations of the total energy of the system require taking into account the initial and boundary conditions and, therefore, too cumbersome. As it is noted above, we are going to avoid all the problems in the following way:
It is proposed to perform two repeating experiments under identical initial and boundary conditions except the only difference, namely, the first experiment must be performed with the given value I of the initial current in the coil of the solenoid, and the second one must be done with I = 0. Obviously, for ideal solenoid, both initial and boundary conditions for the electrical and magnetical fields must be equal one to another in both experiments. So, under assumption that the magnetic field of the solenoid does not influence the USP, the latter must pass along the wire under identical conditions in both experiments, with given value I and with I = 0. Therefore, subtracting the values of the conditions of the first experiment from the corresponding values of the second one, we are obliged to obtain exact zero, i.e. the boundary and initial conditions can be omitted from our consideration. . So while performing calculations, we limit ourselves with the expressions for the total energy of the system which do not consist of the above conditions in explicit form.
Since on the part ab of the wires the plus and minus pulses are weakly connected to one another, we are able to limit our consideration, without loss of generality, only by one wire and one solenoid.
Here, before any calculations, one has to point out on discrepancy between the proposed experiment and the experiments on AB effect. It is shown in [5] (App.A) that, in the latter case, changing of the charge's velocity does not take place. This is caused by performing of the condition I(t) = Const i.e. the solenoid's supply source compensates each changing of the current induced by the magnetic field of the USP.
In this experiment, however, the velocity of passing of the USP in the wire is comparable to the velocity of the light so we have adiabatic regime when the external source cannot provide I(t) = Const.
So let us define I as an initial current that does not change its value during passing the USP at the antenna and consider how the USP influence the solenoid.
When penetrating into the latter, the magnetic field of the USP induces in the coil, on the background of I, a current i; by the way, I and i are independent of one another because the physical cause of inducing of i is the electric field
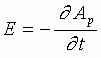
where ![]() is a
vector potential of the USP and it is independent of the external source.
is a
vector potential of the USP and it is independent of the external source.
Let us calculate the energy W of the system when the USP is on the part ab of the wire (we use Gaussian units):
Here, B(I) the magnetic field produced by the
current I in the volume ![]() of the solenoid. For simplicity of calculations, we will carry out the
integration of the magnetic fields over all the space, however, keeping in mind
that the field B(I) does not equal to zero only in an internal
area of the solenoid; besides, both other fields
of the solenoid. For simplicity of calculations, we will carry out the
integration of the magnetic fields over all the space, however, keeping in mind
that the field B(I) does not equal to zero only in an internal
area of the solenoid; besides, both other fields ![]() and
B(i) do not equal to zero in the external area too.
and
B(i) do not equal to zero in the external area too. ![]() is the total energy of the electric field E inside and outside the wire.
is the total energy of the electric field E inside and outside the wire.
It is important to point out - and due to this fact the expected effect is achieved - that when the USP is on part ab of the wire the magnetic fields of the USP and of the solenoid are directed in such a way that their term of interaction
equals to zero. Indeed, B(I) field is directed
along the axis of the solenoid; besides the![]() field circulates around the x axis coinciding with the part ab
of the wire and intersecting z axis at a right angle. So after
integrating over all the space of the solenoid, the term (3)
will be equal to zero (Fig.2).
field circulates around the x axis coinciding with the part ab
of the wire and intersecting z axis at a right angle. So after
integrating over all the space of the solenoid, the term (3)
will be equal to zero (Fig.2).
Obviously, due to the same symmetry it will be equal to zero the term with the current i induced by the USP

when the USP is passing along the part ab of the wire.
Supposing the vector potential of the solenoid does not
influence the USP, i.e. ![]() remains the same, we calculate the total energy when the USP is on the
arc bc:
remains the same, we calculate the total energy when the USP is on the
arc bc:
Actually, the energy of the USP changes while the USP is passing along the wire. But this changing is caused only by the resistance and radiation losses of the current pulse. We describe this changing by the equiation:
![]()
where ![]() is the energy of the electric field of the USP when the peak current of the
pulse passes the middle of the arc bc and
is the energy of the electric field of the USP when the peak current of the
pulse passes the middle of the arc bc and ![]() is the loss of the energy of the pulse while the latter passes from point a
to the middle of the arc bc. The resistance losses (Joule heat) of the
secondary current i are included in the term
is the loss of the energy of the pulse while the latter passes from point a
to the middle of the arc bc. The resistance losses (Joule heat) of the
secondary current i are included in the term ![]() too.
too.
The total energy of the system cannot change at the adiabatic regime so
![]()
Subtracting the Eq.(2) from the Eq.(4), we obtain
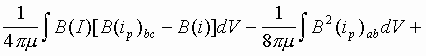
Here, we use the linear dependence of the magnetic field on the current creating that field
![]()
Indeed, the magnetic field defines as a curl of the vector potential; the latter is defined from the (linear) wave equation of which right-hand side dependes linearly on the current. So, the vector potential and, therefore, the magnetic field is defined from the integral but linear operator of the current, and the magnetic field of sum of the currents is the sum of the magnetic fields created by each current independently.
Now let us calculate the total energy of the system in the absence of the initial current in the coil of the solenoid, i.e. at I = 0. When the USP is on the part ab of the wire,
When the USP is on the part bc of the wire the total energy of the system is
Subtracting the Eq.(6) from the Eq.(7), we obtain:
One can easily see now that consequent carrying out of two experiments, with given I and with I = 0, allows to eliminate the count of the secondary current i to the effect of influence the vector potential on the USP. It is achieved by comparing of the results of two experiments: let us subtract the Eq.(8) from the Eq.(5):
Now it is sufficient to carry out the integration only over
the internal area of the solenoid ![]() .
.
Thus, the end parameters of the USP must change due to existing of the last term.
4. Discussion.
Since there is no the energy exchange with the external
sources, this term cannot be equal to zero if only the current i does not
fully shield the field ![]() inside
the solenoid (for example, for superconducting winding of the coil).
inside
the solenoid (for example, for superconducting winding of the coil).
Therefore, to detect the greater effect it is desirable to use the coil with such inductance and resistivity that the value of i would be reduced as much as possible.
Now we should estimate another possible causes of changing of the USP characteristics. The main one is charging of the coil while current passing, the lower end of the coil by the (+) sign and the upper end by (-) sign, for example. However, we can use magnetic materials instead of convenient coil to create the same magnetic field B(I) but now without charging the external side of the solenoid. Obviously, all the above calculations must not change.
Another possibility to change the characteristics is nonidentity of the USP produced by the generator. However, if we find for series of the USP the dependence of power of the radiated signals from the antenna on the value of I, it is sufficient to conclude about reality of the vector potential as a physical quantity.
It would be liked to make one more note about possible influence of the magnetic field which could present outside the solenoid due to nonperfect
design of the latter on the USP. It is known that the component of Lorentz force caused by the magnetic field is always directed transversally to the current, i.e. to the motion of the USP, in this case. Therefore, even the magnetic field created by I would exist outside the solenoid it would not accelerate or decelerate the USP.
It should be noted that, independently of the end results, the proposed experiment is of big physical interest. If the characteristics of the USP coincide in both the cases of the given value of I in the coil and of I = 0, it means that one must introduce into the energy equations an unknown term which should fully compensate the count from the right-hand side of the Eq.(9). However, the main problem is to give a physical explanation of such a term.
If the USP loses its energy in some way, therefore, it should exist a certain object which takes the energy from the USP and transfer to the fields inside the solenoid. It can be solely the vector potential A that forms the potential barrier for the pulse
![]()
where ![]() is the
volume of the piece of the wire at smooth joint from the straightline part ab
to the arc bc. If such a barrier exists in reality the USP should whether
reflect off or decelerate on it. We are able to detect experimentally both these
processes. In the first case, the reflected pulse can be detected in the
generator. In the second one, the decelerating pulse should radiate so the
receiver will register additional signal from the antenna.
is the
volume of the piece of the wire at smooth joint from the straightline part ab
to the arc bc. If such a barrier exists in reality the USP should whether
reflect off or decelerate on it. We are able to detect experimentally both these
processes. In the first case, the reflected pulse can be detected in the
generator. In the second one, the decelerating pulse should radiate so the
receiver will register additional signal from the antenna.
It should be noted that one problem remains, namely, how our considerations corresponds to the gauge invariance. Unfortunately, the author does not know how to resolve this contradiction. The crucial argument in favour of reality of the vector potential as a physical quantity can be obtained from the experimental data. Only then any correspondence of the theory to the experimental data could be discussed.
It is interesting to note that in one experiment performed by Marinov [11] the obtained data can be explained by existence of the vector potential in the classical electrodynamics too. However, in the above experiment, it is very diffcult to perform the energy analysis similar to given one for the proposed experiment. Therefore, it is diffcult to state that changing of the velocities of the electrons in the rared gas tube surrounding the solenoid is caused namely by influence of the vector potential. In opposite to Marinov’s experiment the possible changing of the velocity of the charge is limited by the only cause.
Thus, independently, of the end experimental result, we have three possibilities:
as incorrect;
To the author’s point of view, in the above experiment, the third case must be realized.
Final remark. It is accepted that in the classical electrodynamics not the EM potentials but the EM fields and, therefore, forces are the quantities describing behavior of the system. So it is interesting to analyse what force can be responsible to desceleration of the USP. Obviously, it is not Lorentz force. Mathematically such a force must be calculated as
using the vectorial identity
we obtain from the Eq.(11) four different terms including the term corresponding to the magnetic Lorentz force. However, in this case, the following term
![]()
is responsible for descelerating the USP. From the point of view of the convenient electrodynamics, this term is very unusual because
References.
Author:
V. Onoochin, e-mail: a33am@dol.ru