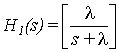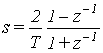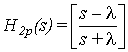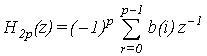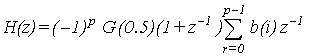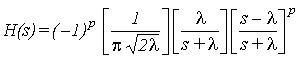|
|
"JOURNAL OF RADIOELECTRONICS" N 10, 2002 |
|
A CNLMS ADAPTIVE FILTER ALGORITHM
Casco Fausto, Amín Omar, Zaharov Viktor and Ekzhanov Alexander.
Tel (5255) 58044637 Fax (5255) 5804 4628 Email:alfa@xanum.uam.mx
key words : System Identification and Parametric Spectrum Estimation
Department of Electrical Engineering,
Universidad Autónoma Metropolitana-Iztapalapa,
México City, México.
Recived 15.10.2002.
This paper propose a Cascaded structure for adaptive digital filtering used with the Normalized Least Mean Square Algorithm (CNLMS) that can be obtained by the expansion of Laguerre´s polynomials, this structure is implemented as a system identifier and is compared with filter structure using the Normalized Least Mean Square Algorithm (LMS) [6] and with the Variable Step Size Algorithm (MVSS) described in [7]. The number of analytical operations is below of the required for the MVSS algorithm. Simulations show that the new architecture decrease the mean square error (MSE) compared with results obtained of comparison with both NLMS and MVSS algorithms, see figures 3 and 4.
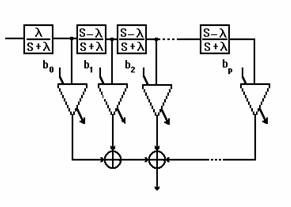
Some variations of the general analog structure of figure 1 was proposed [2] and implemented for spectrum estimation of speech signals (analysis- synthesis) in time and frequency domain [1,3-5]. However, digital transformation of the figure 1 is generally expensive to implement.
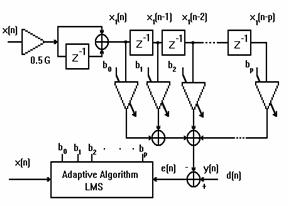
Therefore, figure 2 is the result of the transformation of the analog Laguerre filter [2] and [3] (fig. 1) to its digital equivalent. The explored method combine advantages of FIR and more elaborated filters, like adaptive Lattice filters and the general digital expansion in terms of orthogonal functions, fast convergence as for (FIR) and decreased MSE as for structures Infinite Impulse Response (IIR).
Figure 1. General Analog of Laguerre Filter
2.1. : FIRST STAGE TRANSFER FUNCTION:
The analog transfer function of the first stage is given by:
where :
Equation (1) is the transfer function of a first order
analog low pass (RC) filter, where
l
is the ![]() cutoff frequency in ( rad/sec) of a low pass filter.
In order to obtain the digital equivalent of equation (1) we define
cutoff frequency in ( rad/sec) of a low pass filter.
In order to obtain the digital equivalent of equation (1) we define
lT=T/RC=2, where: T is the sampling period of the digital system. By simple substitution of the bilinear transformation (2) in equation (1), it follows that :
Then the output of the first stage (figure 2) x1(n) is given by:
Note that the gain factor (G) in figure 2 is fixed to one for the analysis and simulation.
Figure 2. CNLMS Adaptive Filter Algorithm
2.2. SECOND STAGE TRANSFER FUNCTION
The correspondence of analog and digital transfer
functions is done with the same assumption as in the first stage;
lT=2, then using the bilinear transformation it can be
shown that ![]() is the analog equivalent of
is the analog equivalent of
![]() , where p is the order of the model:
, where p is the order of the model:
and
then:
Where p is the filter order or taps number, and b(i) is the tap weights. The total transfer function of the model (figure 2) can be obtained by cascading equations (3) and (7) as follows:
It can be shown that (8) is a digital equivalent of the analog Laguerre filter with:
where:
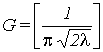 .
.
In the conventional NLMS algorithm [6], the step size is a constant. In the variable step size algorithm (MVSS) [7], the step size m is given by:
where a=0.997 , g=0.00048 and
with 0<b<1
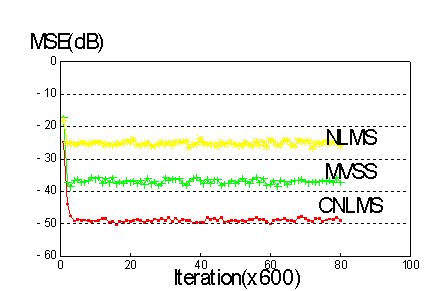
The convergence performance of the three algorithms NLMS,MVSS and CNLMS is shown en figure 3, the three algorithms were simulated as adaptive noise cancellers with the same reference and desired input signals, en this case the algorithms have the same convergence rate for a SNR of 25dB and the CNLMS algorithm gets a Mean Square Error (MSE) of 50 dB (15 dB more than the MVSS algorithm).
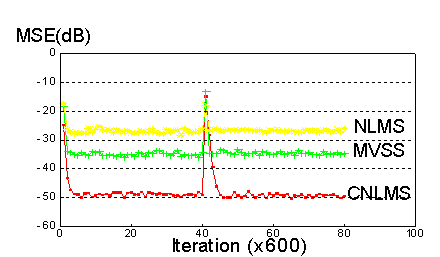
In figure 4 the three algorithms have converged when the impulse response suddenly changed and newly the CNLMS algorithm gets better MSE than MVSS algorithm. Figures 3 and 4 were obtained by an 8 taps filter for each of them.
Figure 3.-Comparison of the conventional NLMS, variable step size MVSS and Normalized Least Mean Square Algorithm with Cascaded structure (CNLMS).The input signal is white noise with a S/N ratio of 25dB for each system’s response
Figure 4. Comparison of the conventional NLMS, variable step size MVSS and Normalized Least Mean Square Algorithm with Cascaded structure (CNLMS). The system’s impulse response is changed suddenly. The input signal is white noise with a S/N ratio of 25 dB for each system’s response
The proposed algorithm offers better MSE than a variable algorithm MVSS and it has high convergence rate without stability problems due the FIR characteristics. The low pass function of the first stage makes this structure ideal for Processing Signals with nature low pass such as speech, audio, etc. The proposed CNLMS algorithm has a simple digital structure to be implemented.
5. REFERENCES
1. Flanagan, J. L., Speech Analysis Synthesis and Perception, Second Edition, Springer -Verlag -Berlin - Heidelberg - New York, 1973.
2. Lee, Y. W., Statistical Theory of Communication. New York, John Wiley & Sons, 1960.
3. Kulya V. I., Application of Laguerre Functions to Parametric Coding of Speech Signals, Journal “Electrosvyaz”, No. 7, pp.33-39, 1962. Also Journal ”Telecommunications and Radio Engineering” No. 7, 34- 41, 1962.
4. Manley, H. J., Klien D. B., Analysis-Synthesis of Continuous Speech in Terms of Orthogonalized Exponentially Damped Sinusoids, J. of Acoust. Soc. Am. 34, 724 (A), 1962.
5. Makhoul, J., Stable and Efficient Lattice Methods for Linear Prediction, IEEE Trans. Acoust., Speech, Signal Processing, vol. ASSP- 25, pp. 423- 428, Oct. 1977.
6. B.Widrow and S.D. Stearns, Adaptive Signal Processing. Prentice Hall, Englewood Cliffs, New Jersey, 1985.
7. Tyseer A.,K. Mayas, A Robust Variable Step-Size LMS type Algorithm: Analysis and Simulations, .IEEE Transactions on Signal Processing,vol.45,no.3, pp 631-639, March 1997.