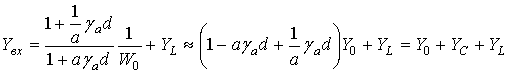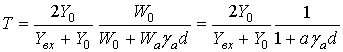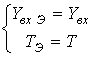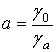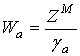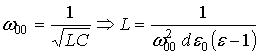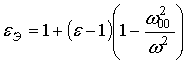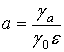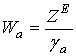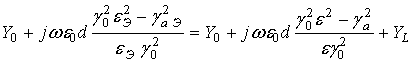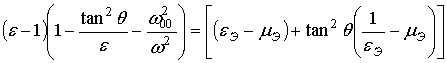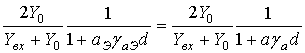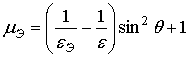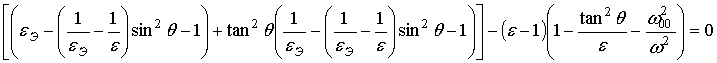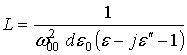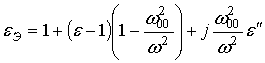МЕТАМАТЕРИАЛ С ПОВЫШЕННОЙ МЕХАНИЧЕСКОЙ ПРОЧНОСТЬЮ И ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТЬЮ БЛИЗКОЙ К ЕДИНИЦЕ
K. M. Басков
Институт теоретической и прикладной электродинамики Российской академии наук
Получена 24 сентября 2013 г.
Аннотация. В статье приводятся исследования метаматериала с диэлектрической проницаемостью близкой к единице. Такой метаматериал может быть использован при создании радиопрозрачных укрытий. Этот материал представляет многослойную диэлектрическую структуру, между слоями которой включены компенсационные решетки индуктивного типа. Для получения дополнительной индуктивности провода в решетке искривляются в виде соленоида. Как показано в работе, дополнительная индуктивность, полученная за счет искривления проводов, позволяет получить прочный материал с высокими радиотехническими характеристиками. Результаты исследований, представленные в статье, были доложены на международной конференции «Излучение и рассеяние электромагнитных волн» (ИРЭМВ-2013).
Ключевые слова: метаматериал, радиопрозрачное укрытие, компенсационные решетки, эквивалентная линия передачи, слоистый диэлектрик.
Abstract. The paper presents the study of a metamaterial with dielectric constant close to unity. Such a metamaterial can be used to create radomes. This material is a multilayer dielectric structure, between layers of which are incorporated compensation grating inductive type. In order to increase the inductance, grid wires are bent in the form of a solenoid. As shown in the paper, additional inductance obtained by curving wire, provides a strong material with high radio-technical characteristics. The research results reported in the paper were presented at the International Conference "Radiation and scattering of electromagnetic waves".
Keywords: metamaterial, radome, compensating lattice, equivalent long line, sandwich dielectric structure.
Введение
Для создания радиопрозрачных укрытий (РПУ) с улучшенными радиотехническими характеристиками (РТХ) могли бы использоваться материалы с диэлектрической проницаемостью близкой к единице. Обычные материалы с низкой диэлектрической проницаемостью представляют собой либо вспененные материалы (пенопласты, вспененные полиэтилены или фторопласты), либо различные сотовые структуры. Так как в таких материалах основную долю их объема составляют воздушные полости, их прочность очень низкая. Использование таких материалов для производства РПУ, которые испытывают при эксплуатации серьезные механические нагрузки, недопустимо.
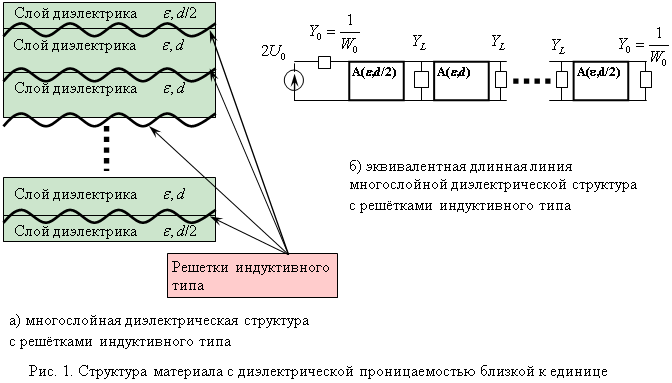
На рис. 1а представлена многослойная конструкция, которая может рассматриваться как некоторый метаматериал с близкой к единице диэлектрической проницаемостью, обладающий при этом высокой прочностью. Конструкция представляет собой чередующиеся слои диэлектрической матрицы (например, стеклопластика) с малой электрической толщиной и некоторые поверхности с индуктивной проводимостью. В качестве поверхностей с индуктивной проводимостью лучше всего использовать решётки из искривлённых проводов. В [1] показано, что решетка из искривленных проводов по своим электродинамическим свойствам максимально приближена к поверхности с индуктивной проводимостью, эквивалентная индуктивность которой не зависит ни от частоты и ни от угла падения волны. Электродинамический анализ представленной многослойной структуры может быть выполнен методом эквивалентных длинных линий, который подробно описан в [2]. Эквивалентная длинная линия структуры представлена на рис. 1б.
Во многих работах, например, в [3,4], рассматриваются стенки РПУ с реактивными включениями в виде решёток из прямых проводов. В работе показано, что использование прямых проводов менее эффективно, как с точки зрения РТХ, так и технологии производства РПУ.
1. Расчёт эквивалентных электродинамических параметров нового материала
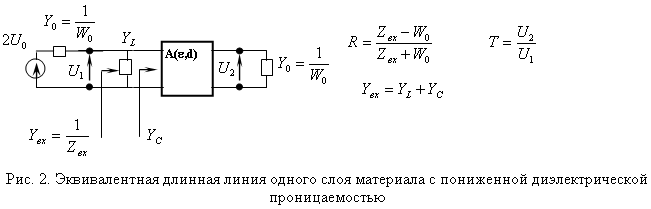
Как будет показано ниже, эквивалентные диэлектрическая и магнитная проницаемости eЭ и mЭ структуры, представленной на рис.1а, не зависят от количества слоев, поэтому их вывод можно провести для одного слоя структуры. Используя теорию длинных линий (рис. 2) [2], получаем выражения для входного адмитанса Yвх и коэффициент пропускания (КП) T одного слоя метаматериала с учётом того, что слой диэлектрика бесконечно тонкий. При этом в схеме рис. 2 удобнее использовать проводимости, так как все подключения параллельные:
где 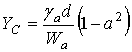 -
эквивалентная ёмкостная проводимость слоя диэлектрика;
-
эквивалентная ёмкостная проводимость слоя диэлектрика; 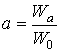 ;
; 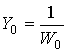 -
адмитанс свободного пространства; Wа – импеданс матрицы;
-
адмитанс свободного пространства; Wа – импеданс матрицы; ![]() ; q - угол падения; e и m - диэлектрическая и магнитная проницаемости матрицы; d – толщина одного слоя матрицы;
; q - угол падения; e и m - диэлектрическая и магнитная проницаемости матрицы; d – толщина одного слоя матрицы; ![]() - эквивалентная индуктивная проводимость
решётки из искривлённых проводов, индуктивность которой не зависит ни от
частоты, ни от угла падения волны [1,6]; k0 – постоянная распространения волны в свободном
пространстве; w
- круговая частота волны.
- эквивалентная индуктивная проводимость
решётки из искривлённых проводов, индуктивность которой не зависит ни от
частоты, ни от угла падения волны [1,6]; k0 – постоянная распространения волны в свободном
пространстве; w
- круговая частота волны.
В данном разделе e является действительной величиной, т.е. предполагается, что материал диэлектрической матрицы не имеет электрических потерь.
Для того, чтобы получить эффективные параметры eЭ и mЭ, необходимо решить систему уравнений:
где Yвх Э и ТЭ адмитанс и КП для слоя диэлектрика толщиной d с диэлектрической и магнитной проницаемостью eЭ и mЭ
Для перпендикулярной поляризации падающей волны можно записать:
где ![]() ;
; ![]() ; m0 = 1,27 10-6 Гн/м; m=1 – радиопрозрачные материалы для
изготовления РПУ немагнитные.
; m0 = 1,27 10-6 Гн/м; m=1 – радиопрозрачные материалы для
изготовления РПУ немагнитные.
Тогда:
где e0 = 8,85 10-12 Ф/м, 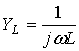 ,
L – эквивалентная индуктивность в
поверхностной проводимости решётки [1,6].
,
L – эквивалентная индуктивность в
поверхностной проводимости решётки [1,6].
Для минимального
отражения от такой структуры на заданной частоте, необходимо, чтобы
эквивалентные проводимости диэлектрика и индуктивного слоя компенсировали друг
друга, при этом должно быть равенство ![]() и YС по модулю. Вводится понятие частоты
настройки метаматериала:
и YС по модулю. Вводится понятие частоты
настройки метаматериала:
Если подставить (5) в (4), то получится:
Решение (6) также удовлетворяет и второму уравнению в системе (2) для КП. Т.е. при перпендикулярной поляризации эффективная диэлектрическая проницаемость метаматериала не зависит от угла падения волны и может быть вычислена по формуле (6). Для частот меньших w00 эффективная диэлектрическая проницаемость меньше единицы и стремится к минус бесконечности. Для частот больших w00 эффективная диэлектрическая проницаемость материала стремится к диэлектрической проницаемости матрицы. Эквивалентная магнитная проницаемость при этом остаётся равной единице.
Для параллельной поляризации падающей волны:
где 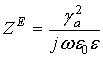
Тогда первое уравнение системы (2) примет вид:
где ![]()
В итоге:
Второе уравнение системы (2) с учётом (7) записывается в виде:
После преобразований получается уравнение:
Из (11) можно получить выражение для mЭ:
После подстановки (12) в (9) получается уравнение для нахождения eЭ :
Решение уравнения (13) даёт то же выражение (6) для eЭ, что выражение для эффективной диэлектрической проницаемости при перпендикулярной поляризации падающей волны. При параллельной поляризации падающей волны появляется эффективная магнитная проницаемость не равная единице и зависящая от угла падения.
На рис. 3а представлены частотные зависимости эквивалентной диэлектрической проницаемости при трех значениях диэлектрической проницаемости матрицы. Видно, что крутизна зависимости eЭ от частоты тем меньше, чем меньше e. Эквивалентная магнитная проницаемость зависит от угла падения при параллельной поляризации падающей волны и может быть вычислена по формуле (12). На рис. 3б-е представлены угловые зависимости mЭ при тех же значениях e. С ростом угла падения эквивалентная магнитная проницаемость при eЭ>0 растет, а при eЭ<0 падает. При этом максимальная крутизна угловой зависимости эквивалентной магнитной проницаемости наблюдается на так называемой плазменной частоте w0, где eЭ=0. При переходе через плазменную частоту наклон угловой зависимости mЭ меняется скачком. Кроме этого, при eЭ =1 крутизна угловой зависимости mЭ тем больше, чем больше значение диэлектрической проницаемости матрицы рассматриваемого метаматериала. С ростом частоты крутизна угловой зависимости mЭ уменьшается, а рассматриваемый материал приближается к свойствам диэлектрика, из которого сделана матрица.
Можно сделать вывод, что рассматриваемый материал обладает не только частотной дисперсией эффективной диэлектрической проницаемости, но и пространственной дисперсией эффективной магнитной проницаемости. Пространственная дисперсия эффективной магнитной проницаемости является отрицательным свойством рассматриваемого материала, так как приведет не только к увеличению отражений от стенки РПУ, но и увеличит фазовые искажения фронта волны при прохождении стенки РПУ при параллельной поляризации.
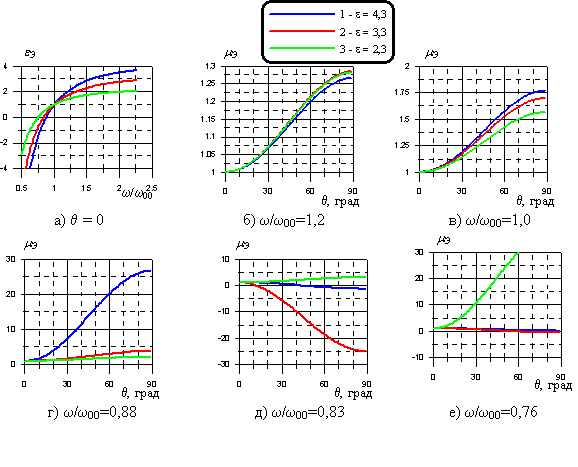
Рис. 3. Частотные а) и угловые б)-е) зависимости эффективных параметров метаматериала.
2. Учет потерь в диэлектрической матрице
В первом разделе статьи был рассмотрен случай, когда значение диэлектрической проницаемости матрицы было действительным, т.е. рассматривался диэлектрик без потерь. Если диэлектрическая проницаемость матрицы является комплексной величиной, то это эквивалентно включению в длинную линию некоторой малой шунтирующей проводимости. Индуктивную проводимость, описывающую решетку, можно считать чисто мнимой величиной. Это справедливо, если период решетки достаточно мал, а провода в решётке обладают малым удельным сопротивлением. В этом случае при выводе формул эффективных диэлектрической и магнитной проницаемостей надо изменить формулу (5):
где e = e’ + j e’’ –комплексная диэлектрическая проницаемость матрицы.
Если учесть (14), то формула (6) примет вид:
Т.е. мнимая часть эффективной диэлектрической проницаемости равна мнимой части диэлектрической проницаемости матрицы. Тангенс угла диэлектрических потерь при этом на частоте настройки материала возрастает в e раз. Отсюда следует, что для рассматриваемого материала требуется матрица с минимальными потерями.
Эффективная магнитной проницаемости равна мнимой части значения выражения (12). Она оказывается положительной в отличие от обычных материалов. На рис. 4 приведены графики угловых зависимостей мнимой части эквивалентной магнитной проницаемости материала mЭ’’ для разных значений частоты при диэлектрической проницаемости матрицы 4,3 – j0,043. Как и для действительной части, максимальная крутизна угловой зависимости наблюдается на частоте при eЭ=0.
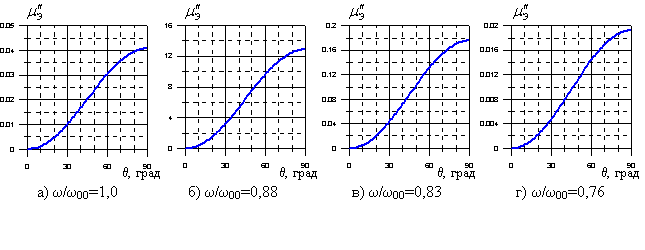
Рис. 4. Угловые зависимости мнимой части эффективной магнитной проницаемости на разных частотах при e = 4,3 – j 0,043
3. Проверка полученных формул точным методом интегральных уравнений
Для проверки правильности результатов и реализуемости материала, описанного в первых двух разделах, были проведены расчёты значений эффективных диэлектрических и магнитных проницаемостей слоистых структур на основе диэлектрической матрицы с e = 4,3 методом интегральных уравнений (ИУ). Эти результаты расчётов сравнивались с эффективными параметрами (15) и (12) идеального метаматериала с бесконечно малой толщиной слоёв матрицы. Рассматривались следующие варианты многослойной структуры:
1-й вариант: 8 слоёв толщиной d=2,0 мм с общей толщиной 16,0 мм (также был рассмотрен вариант из 4-х слоёв общей толщиной 8,0 мм)
2-й вариант: 4 слоя толщиной d=4,0 мм общей толщиной 16,0 мм
3-й вариант: 2 слоя толщиной d=8,0 мм общей толщиной 16,0 мм
Расчёт эффективных параметров методом ИУ проводился следующим образом: сначала рассчитывались коэффициенты отражения (КО) и КП, потом по этим коэффициентам подбирались эффективные параметры для слоя магнитодиэлектрика той же толщины, что и общая толщина слоистой структуры.
Для всех вариантов выбиралась индуктивная решётка из изогнутых проводов с периодом 2,5 мм таким образом, чтобы частота настройки материала была равна 5,0 ГГц. Для первого варианта при толщине провода 0,150 мм (0,75 мм для круглого провода) дополнительная индуктивность требовалась 16 нГн/квадрат [1,6]. Соленоид с такой дополнительной индуктивностью вполне реализуем: диаметр соленоида 0,3 мм, а шаг соленоида 0,118 мм. Для второго варианта требовалась дополнительная индуктивность, получаемая за счет искривлений проводов решетки: 7,28 нГн/квадрат. Для третьего варианта дополнительная индуктивность должна быть: 3,04 нГн/квадрат.
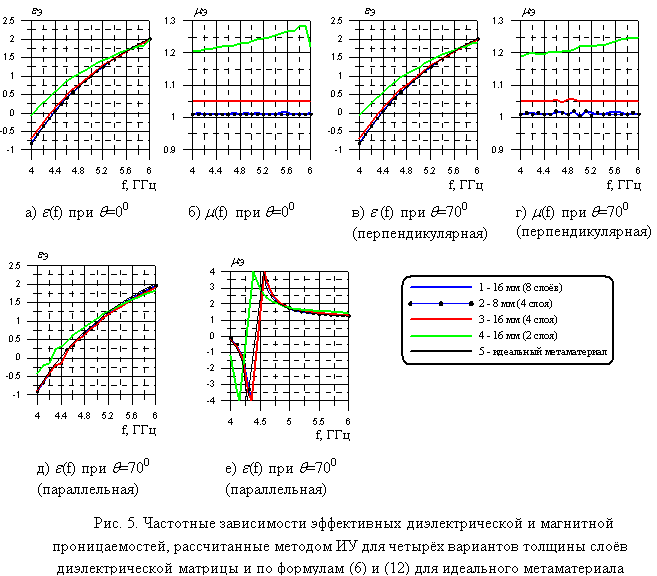
На рис. 5 приведены частотные зависимости эффективных диэлектрических и магнитных проницаемостей при отсутствии потерь в диэлектрической матрице. Можно заметить, что у 1-го варианта эффективные параметры максимально близко соответствуют эффективным параметрам идеального метаматериала. У 2-го и 3-го вариантов наблюдаются отличия эффективных параметров от параметров идеального метаматериала с бесконечно тонкими слоями диэлектрической матрицы. При увеличенных толщинах слоёв матрицы эффективная магнитная проницаемость не равна 1. Толщины слоёв многослойной структуры для данного примера не должны превышать 0,07 – 0,1 длины волны в материале матрицы, тогда рассматриваемая многослойная структура будет максимально близко соответствовать свойствам идеального метаматериала, эффективные параметры которого рассчитываются по формулам (6) и (12).
На рис. 6 приведены рассчитанные двумя методами угловые зависимости эквивалентных параметров 1-го варианта (d=2 мм) многослойной структуры толщиной 16 мм при тангенсе угла диэлектрических потерь в матрице 1% (e=4,3 – j 0,043) на частотах 5 и 6 ГГц. Видно, что эффективные параметры 1-го варианта и при наличии потерь в матрице очень близки к эффективным параметрам идеального метаматериала.
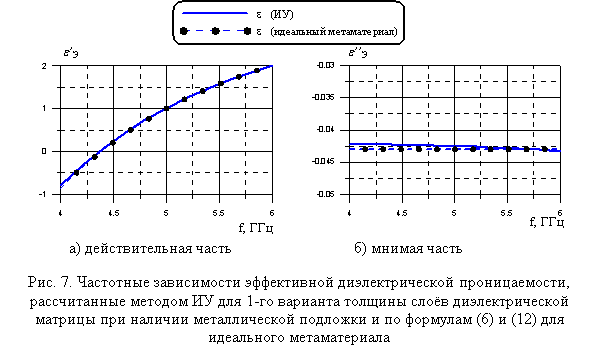
На рис. 7 приведены графики частотных зависимостей действительной и мнимой частей эквивалентной диэлектрической проницаемости 1-го варианта (d=2 мм) многослойной структуры толщиной 16 мм при тангенсе угла диэлектрических потерь в матрице 0,01 (e=4,3 – j 0,043) при наличии металлической подложки и нормальном падении волны. Подбор эффективной диэлектрической проницаемости осуществлялся только по КО. Графики зависимостей практически совпадают с графиками частотной зависимости e’Э и e’’Э для идеального метаматериала. Можно сделать вывод, что наличие металлической подложки не влияет на эквивалентные параметры рассматриваемой структуры.
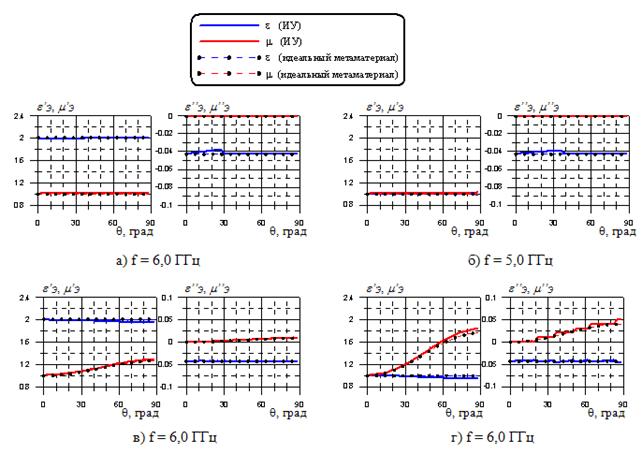
Рис. 6. Угловые зависимости эффективных диэлектрической и магнитной проницаемостей на разных частотах при e = 4,3 – j 0,043 и d = 2,0 мм.
а) и б) – перпендикулярная поляризация; в) и г) – параллельная поляризация
Из приведенных примеров можно сделать вывод, что слоистая структура с решётками из искривлённых проводов (рис. 1а) при толщине слоёв 0,07 – 0,1 длин волн в материале диэлектрической матрицы, эквивалентна однородному материалу с частотной дисперсией диэлектрической проницаемости на обеих поляризациях падающей волны и пространственной дисперсией магнитной проницаемости при параллельной поляризации. Диэлектрическую и магнитную проницаемости такого материала можно вычислить по формулам (15) и (13). Для получения оптимальной стенки РПУ вместо анализа сложной многослойной диэлектрической структуры с реактивными решётками можно использовать эквивалентные параметры, применяя при этом обычные методы оптимизации стенки РПУ.
4. Обоснование необходимости использования решётки из искривлённых проводов
Известно, что решётку из прямых проводов можно рассматривать как некоторую поверхность с индуктивной проводимостью. Как было показано в [1], решётки из прямых проводов при параллельной поляризации падающей волны обладают эквивалентной индуктивностью, которая с ростом угла падения уменьшается. Это привёт к тому, что при такой поляризации будет высокий уровень отражения от метаматериала. Кроме этого у решёток из прямых проводов есть ещё один недостаток. Для электродинамического согласования тонких диэлектрических слоёв требуется достаточно большой период решётки. Это приводит к зависимости индуктивности в поверхностной проводимости решётки от угла падения волны и от угла ориентации вектора распространения волны (рис. 8). Т.е. свойства слоистой диэлектрической структуры с решётками из прямых проводов не будут соответствовать свойствам идеального метаматериала. При производстве РПУ, форма которого обладает некоторой кривизной, а защищаемый объект сканирует в пространстве, ориентировать решётку нужным образом не удастся.

Для примера были рассмотрены два варианта метаматериала, настроенных на частоту f00 = 5 ГГц, с матрицей e = 4,3 и толщиной d = 2 мм. В 1-м варианте использовалась решётка из прямых проводов, а во 2-м варианте – из искривленных проводов. В обоих случаях использовался плоский провод шириной 150 мкм (или круглый провод диаметром 75 мкм: решётки из круглых проводов с диаметром b эквивалентны решёткам из плоских проводов шириной 2b [5]). В 1-м варианте потребовался период оешётки – 18,5 мм. При использовании искривленных проводов период решётки был выбран 2,5 мм. Искривления проводов в виде соленоида диаметром 0,3 мм и шагом витков 118 мкм давали дополнительную индуктивность 16 нГн на квадрат [1,6], что позволило обеспечить электродинамическое согласование на частоте 5 ГГц.
На рис. 9 представлены
вычисленные методом ИУ частотные зависимости модуля КО и фазы КП, нормированной
на величину ![]() , при нормальном и наклонном падении под
углом 600 электромагнитной волны. Можно заметить, что для
нормального падения оба варианта абсолютно идентичны. При наклонном падении
волны при перпендикулярной поляризации заметно изменяется частота настройки 1-го
варианта, что связано с достаточно большим требуемым периодом решётки из прямых
проводов. При наклонном падении, если вектор распространения ориентирован
относительно периода решётки под углом j = 450, у 1-го варианта наблюдаются изменение
частоты настройки в сторону высоких частот. Из этого можно сделать вывод, что
первый вариант не будет соответствовать метаматериалу, описанному в первой
части статьи. Кроме этого, уровень отражения у 1-го варианта при наклонном
падении волны при параллельной поляризации заметно выше, что связано с
уменьшением эквивалентной индуктивности у решётки из прямых проводов с
увеличением угла падения (рис. 10 в).
, при нормальном и наклонном падении под
углом 600 электромагнитной волны. Можно заметить, что для
нормального падения оба варианта абсолютно идентичны. При наклонном падении
волны при перпендикулярной поляризации заметно изменяется частота настройки 1-го
варианта, что связано с достаточно большим требуемым периодом решётки из прямых
проводов. При наклонном падении, если вектор распространения ориентирован
относительно периода решётки под углом j = 450, у 1-го варианта наблюдаются изменение
частоты настройки в сторону высоких частот. Из этого можно сделать вывод, что
первый вариант не будет соответствовать метаматериалу, описанному в первой
части статьи. Кроме этого, уровень отражения у 1-го варианта при наклонном
падении волны при параллельной поляризации заметно выше, что связано с
уменьшением эквивалентной индуктивности у решётки из прямых проводов с
увеличением угла падения (рис. 10 в).
Если использовать 1-й вариант метаматериала с реактивной решёткой из прямых проводов для производства РПУ, то для оптимизации структуры стенки нельзя использовать эффективные параметры eЭ и mЭ. Необходимо рассматривать такой слой диэлектрика с решёткой как некоторую периодическую структуру. Если стенка РПУ будет сложной конструкции из нескольких слоев метаматериала, то указанные изменения характеристик при наклонном падении могут существенно усиливаться. Если решётки в разных зонах поверхности РПУ, сделанного из 1-го варианта метаматериала, будут ориентированы по-разному, разные участки фронта волны, проходящего через стенку РПУ, будет испытывать разные набеги фазы. Это приведёт к серьёзным искажениям в ДН укрываемого объекта.
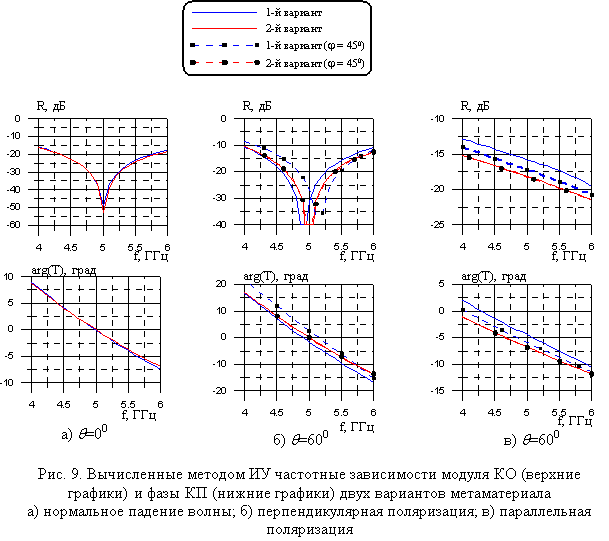
5. Экспериментальное исследование метаматериала с диэлектрической проницаемостью близкой к единице
С целью подтверждения полученных результатов исследований был изготовлен образец метаматериала с диэлектрической проницаемостью близкой к единице размером 400 х 400 мм. В диэлектрическую матрицу из полиуретана толщиной d = 3,5 мм с диэлектрической проницаемостью e = 3,2 – j 0,35 была помещена решётка из искривлённых в виде соленоида проводов. Провода диаметром 0,1 мм в решётке наматывались на леску диаметром 1,3 мм (в расчётах диаметр соленоида принимался равным 1,45 мм) с шагом 0,7 мм. Период решётки был 10 мм. Дополнительная индуктивность в поверхностной проводимости решётки, полученная за счёт искривлений проводов, 42 нГн на квадрат [1,6]. Фотография образца представлена на рис. 10.

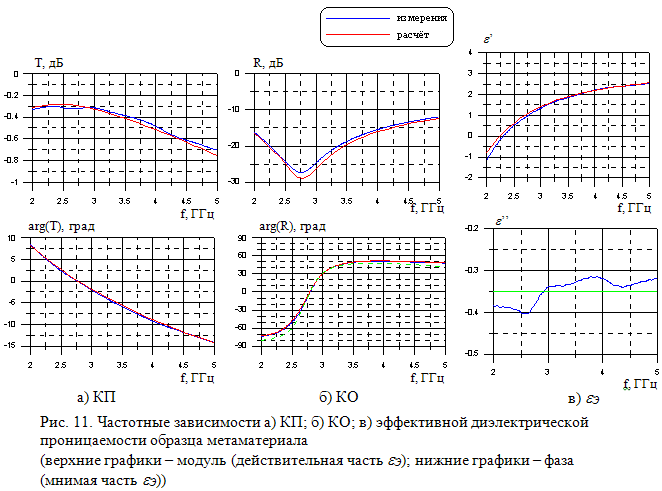
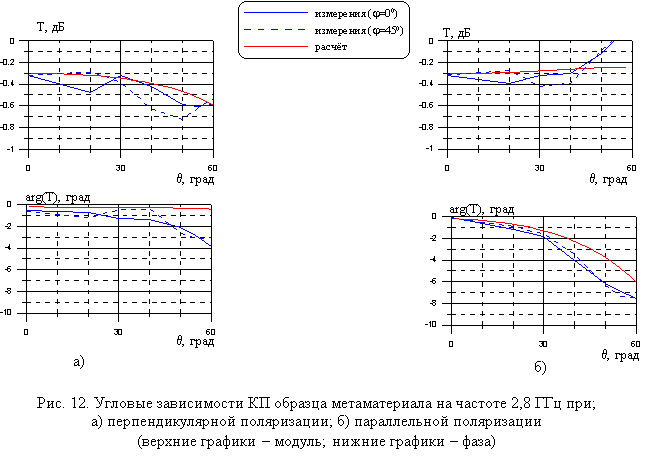
На рис. 11а-б представлены измеренные частотные зависимости КП и КО этого образца метаматериала при нормальном падении, на рис. 11 в представлена измеренная частотная зависимость диэлектрической проницаемости. На рис. 12 представлены измеренные угловые зависимости КП при двух поляризациях падающей волны. Также на рис. 11 и 12 представлены результаты расчёта этих зависимостей методом ИУ. Как видно, результаты расчёта и измерений достаточно хорошо совпадают.
Особое внимание надо обратить на угловые зависимости фазы КП (нижние графики рис. 12). Можно заметить, что крутизна угловой зависимости фазы КП существенно меньше при перпендикулярной поляризации падающей волны, что соответствует приведенным выше исследованиям. Кроме этого на рис. 12 приведены графики угловых зависимостей для случая, когда вектор распространения волны ориентирован по отношению к периоду решётки под углом j = 450. Как можно заметить, изменение ориентации вектора распространения волны относительно периода решётки не оказывает существенного влияния на КП. Если бы решётка была выполнена из прямых проводов с необходимым достаточно большим по отношению к длине волны периодом, то зависимости КП гораздо больше отличались друг от друга при разной ориентации вектора распространения волны.
6. Некоторые примеры применения метаматериала для создания радиопрозрачных укрытий
Если требуется создать РПУ с достаточно прочной стенкой большой толщины для защиты объекта, то описанный материал может обеспечить низкий уровень отражения от стенки РПУ в широком диапазоне частот при близком к нормальному падению волны на стенку.
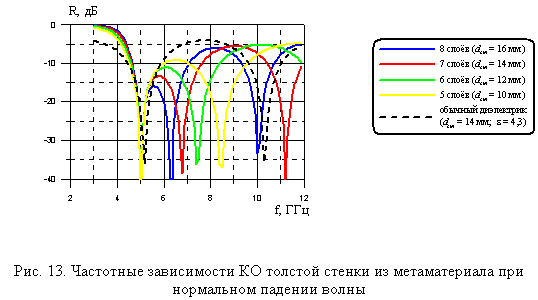
На рис. 13 приведены частотные зависимости КО, рассчитанные методом ИУ, для монолитной стенки, выполненной из 1-го варианта метаматериала, который рассматривался в 3-м пункте статьи (e = 4,3; d = 2,0 мм). Частотные зависимости КО рассчитывались для разного количества слоёв материала, т.е. для разной общей толщины стенки dст. Видно, что для такой стенки РПУ существуют две частоты с низким уровнем КО. Нижняя частота соответствует частоте настройки материала, а верхняя частота соответствует случаю, когда толщина стенки равна половине длины волны в метаматериале. С уменьшением толщины стенки (при уменьшении количество слоёв) верхняя частота, на которой наблюдается низкий уровень КО, увеличивается. Нижняя частота, соответствующая настройке материала, сохраняется. Таким способом можно увеличивать рабочую полосу частот РПУ.
По уровню -10 дБ для такой диэлектрической проницаемости матрицы можно добиться отношения верхней и нижней частоты рабочей полосы частот стенки равной двум. Для обычной монолитной полуволновой стенки, изготовленной из диэлектрика матрицы (e = 4,3) отношение верхней и нижней частот для полосы частот с уровнем КО -10 дБ составляет всего 1,3.
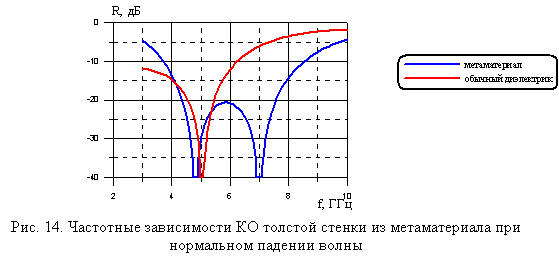
Часто для снижения веса РПУ используют трёхслойную конструкцию стенки, которая может обеспечить низкий уровень КО в достаточно большом диапазоне частот. Такая стенка состоит из двух тонких слоёв достаточно прочного диэлектрика (обшивки), между которыми обычно находится сотовый слой. На рис. 14 приведены частотные зависимости двух вариантов трёхслойной стенки. В 1-м варианте слои обшивки выполнены из одного слоя метаматериала, который был представлен в 3-м пункте статьи (e = 4,3; d = 2,0 мм). Толщина сотового слоя составляет 7,5 мм, а его диэлектрическая проницаемость 1,1. Во 2-м варианте слои обшивки выполнены из диэлектрика толщиной 2 мм и диэлектрической проницаемостью 4,3. Толщина сотового слоя 10 мм. 1-й вариант стенки обеспечивает полосу рабочих частот с уровнем КО от стенки -20 дБ с отношением верхней к нижней частоте 1,74, тогда как у 2-го варианта это отношение составляет всего 1,2. Можно заметить, что у 1-го варианта нижняя частота с низким уровнем КО меньше частоты настройки материала. Это связано с тем, что диэлектрическая проницаемость сотового слоя не равна единице. Это необходимо учитывать при оптимизации конструкции стенок РПУ.
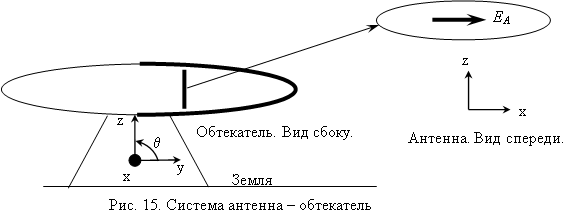
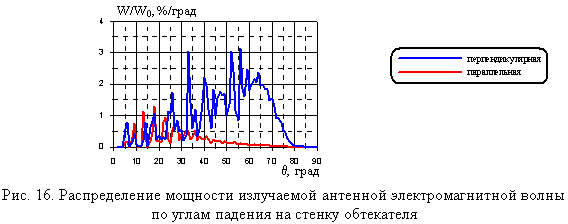
Представленный материал может быть эффективен, если необходимо сделать стенку РПУ с малыми фазовыми искажениями в случае, когда волна падает на стенку преимущественно при перпендикулярной поляризации. Примером такого РПУ является обтекатель в виде тела вращения образующей в виде половины эллипса, как на рис. 15 (вращение вокруг оси Z). На рис. 16 приведено характерное для такого обтекателя распределение мощности излучаемой антенной электромагнитной волны по углам падения на стенку для двух основных поляризаций, если поляризация поля E антенны горизонтальная (вдоль оси Х). Волна проходит стенку такого обтекателя в основном при перпендикулярной поляризации при разных углах падения от 0 до 750.
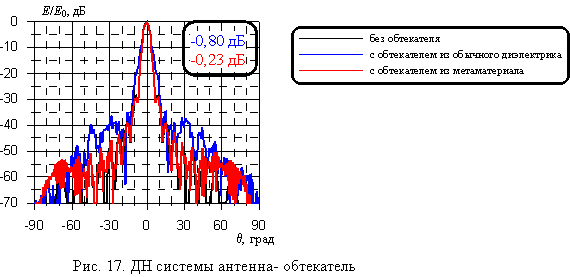
Для иллюстрации преимуществ, которые даёт применение метаматериала при производстве обтекателя такой формы, были рассчитаны на частоте 3 ГГц ДН в плоскости (H) системы антенна – обтекатель для двух вариантов стенки: 1) пятислойная стенка из обычного диэлектрика (e=4,34 – j 0,056) с оптимальными параметрами слоёв; 2) пятислойная стенка из метаматериала с матрицей e = 4,34 – j 0,056, настроенного на частоту 3 ГГц. Расчёт ДН системы антенна – обтекатель осуществлялся методом ФО [7]. На рис. 17 представлены рассчитанные ДН антенны без обтекателя и антенны с двумя вариантами обтекателя в вертикальной (Н) плоскости. Видно, что применение метаматериала позволяет: 1) существенно увеличить прозрачность обтекателя (в квадратной вставке на рис. 17 представлены КП 2-х вариантов обтекателя); 2) избавиться от существенного расширения главного лепестка ДН, связанного с фазовыми искажениями фронта волны при прохождении 1-го варианта стенки обтекателя; 3) снизить общей уровень бокового излучения, связанного с отражением от стенок.
Необходимо заметить, что указанные улучшения РТХ обтекателя такой формы при использовании для его производства метаматериала сохраняются в достаточно большом диапазоне частот (десятки процентов от частоты настройки метаматериала).
Заключение
В статье были исследованы свойства метаматериала, который обладает диэлектрической проницаемостью близкой к единице в некоторой полосе частот. Этот материал может быть эффективен для производства РПУ с улучшенными РТХ. РПУ, стенки которых выполнены из такого материала, могут работать в широком диапазоне частот, вносить меньше искажений в излучение укрываемых объектов, обладать высокой механической прочностью. Особенно эффективно использование рассмотренного метаматериала в том случае, когда волна от укрываемого объекта падает на стенку РПУ преимущественно при перпендикулярной поляризации.
Рассмотренный метаматериал имеет некоторые недостатки. Во-первых, он дисперсионный, что ограничивает его применение для сверхширокополосных объектов. Во-вторых, он обладает пространственной дисперсией магнитной проницаемости при параллельной поляризации падающей волны, что ухудшает прозрачность РПУ и увеличивает фазовые искажения. В-третьих, у этого метаматериала повышенное значение тангенса угла диэлектрических потерь.
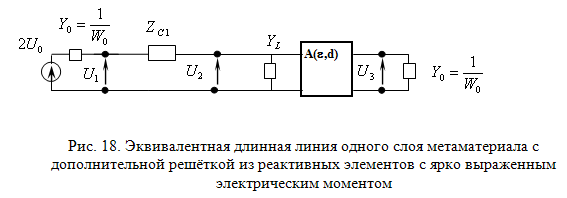
Второй недостаток может быть устранён в некоторой полосе частот с помощью решёток из реактивных элементов, обладающих ярко выраженным электрическим моментом, направленным перпендикулярно поверхности метаматериала. В этом случае включение такой решётки в состав многослойной структуры эквивалентно последовательному включению некоторого реактивного сопротивления в эквивалентной длинной линии ZC1 (рис. 18). Если это сопротивление будет зависеть от угла падения волны по формуле (16), то метаматериал не будет обладать пространственной дисперсией.
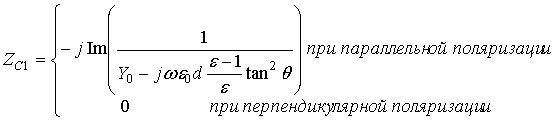 (16)
(16)
Рассмотренный метаматериал сохраняет свои свойства в присутствии других слоёв диэлектрика, а также при наличии металлической подложки. Это позволяет использовать при проектировании различных объектов обычные методы, заменяя рассмотренную многослойную структуру однородным материалом с эффективными значениями eЭ и mЭ.
[1] ”Стенка радиопрозрачного укрытия, состоящая из диэлектрических слоев и компенсационных металлических решеток ”. Басков К.М.// Журнал радиоэлектроники. № 12, 2011 год. URL: http://jre.cplire.ru/jre/dec11/14/text.html
[2] “Математическое моделирование устройств СВЧ и антенн”. В.В. Бодров, В.И. Сурков. Москва, Издательство МЭИ. 1994 г.
[3] Каплун В.Л. “Обтекатели антенн СВЧ” М: Советское радио, 1974 год.
[4] Патент 2000114408/09, 05.06.2000. “Радиопрозрачная стенка обтекателя”. Опубликован 10.06.2001. Изобретатели: Акопян И.Г., Старков Е.А., Сухов А.М., Турко Л.С. Заявитель: Федеральное государственное унитарное предприятие – Московский научно-исследовательский институт “Агат”.
[5] “Радиолокационные отражатели” В.О. Кобак. Изд. “Советское радио”, 1975 г. Стр. 34.
[6] “Расчет индуктивностей”. П.Л. Калантаров, Л.А. Цейтлин. Издательство “Энергоатомиздат”. Ленинград. 1989 г.
[7] “Three-dimensional computational analysis of radomes”. Toru Uno, Saburo Adachi, Kunio Sawaya // Radio Science. November 1987, Vol. 22, №6, pp. 913-916.