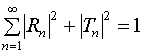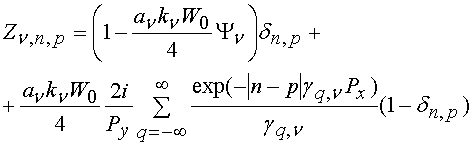УДК 621.396.67
ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ ГЕНЕРАЦИИ ВТОРОЙ ГАРМОНИКИ В НЕЛИНЕЙНОМ РЕЗОНАТОРЕ НА ОСНОВЕ ЭЛЕКТРОМАГНИТНОГО КРИСТАЛЛА
С. Е. Банков, М. Д. Дупленкова, Е. В. Фролова
ИРЭ им. В.А. Котельникова РАН
Получена 30 августа 2013 г.
Аннотация. Исследуется эффект генерации второй гармоники в нелинейном резонаторе, сформированном внутри электромагнитного кристалла, который выполнен в виде периодической решетки металлических цилиндров с нелинейными емкостями, расположенными в плоском волноводе. Рассматривается математическая модель структуры, которая основана на совместном решении линейной граничной задачи для электромагнитного поля и нелинейной задачи для токов и напряжений на нелинейных элементах. Изучены резонаторы с односторонним и двусторонним возбуждением. Показано, что в резонаторе с односторонним возбуждением возможно почти полное преобразование энергии волны основной в энергию волны удвоенной частоты.
Ключевые слова: электромагнитный кристалл, нелинейный электромагнитный кристалл, генерация второй гармоники, собственные колебания, резонансные частоты.
Abstract. Effect of second harmonic generation in non-linear resonator inside electromagnetic crystal formed by an array of metal cylinders with non-linear capacitors located in parallel plate waveguide is investigated. Mathematical model of the structure based on the simultaneous solution of electromagnetic boundary problem and non-linear problem for voltages and currents in non-linear elements is considered. Resonators with single and double-sided excitation are studied. It is shown that in resonator with single-sided excitation energy of wave with dominant frequency may be almost completely transformed in energy of wave with doubled frequency.
Keywords: electromagnetic crystal, nonlinear electromagnetic crystal, second harmonic generation, natural oscillations, resonance frequencies.
1. Постановка задачи
Данная работа посвящена исследованию взаимодействия электромагнитных волн в нелинейных периодических структурах СВЧ диапазона, получивших название электромагнитных кристаллов (ЭМК). Она является продолжением работ [1–5], в которых исследовались ЭМК, образованные решеткой металлических цилиндров, расположенных внутри плоского волновода (ПВ), под которым понимаются два идеально проводящих параллельных друг другу экрана. Цилиндры имеют зазоры, в которые включены нелинейные емкостные элементы.
В работе [1] построена модель нелинейного ЭМК конечной длины по одной координате в виде системы нелинейных уравнений, а в работе [2] получено приближенное решение системы для полубесконечного ЭМК. В работе [3] представлены результаты численного и аналитического исследования нелинейного ЭМК в режиме пространственного синхронизма двух прямых волн, распространяющихся внутри структуры на основной и удвоенной частотах. В работах [4] и [5] исследуется режим пространственного синхронизма прямой и обратной волн, которые распространяются соответственно на основной и удвоенной частотах.
Режим пространственного синхронизма является частным случаем режима накопления слабых нелинейных взаимодействий, которые возникают на отдельных элементах ЭМК. Если слабые эффекты суммируются, как это имеет место в режиме накопления, то интегральный эффект может существенно менять общую физическую картину. Поэтому режимы накопления представляют наибольший интерес при исследовании нелинейных взаимодействий в ЭМК.
Наряду с пространственным синхронизмом можно выделить резонансный режим, в котором слабые эффекты суммируются, а результат их сложения порождает новый комплекс резонансных явлений. Пространственный синхронизм в ЭМК возможен в регулярной структуре. Для его возникновения достаточно выполнить определенные соотношения между параметрами ЭМК. Резонанс в регулярном ЭМК невозможен, так в нем отсутствуют условия для накопления электромагнитной энергии. Для создания таких условий необходимо нарушить регулярность ЭМК, то есть целенаправленно изменить его структуру.
В литературе по фотонным кристаллам и ЭМК известен подход к созданию высокодобротных резонаторов, основанный на введении дефектов в регулярную периодическую структуру, которая находится в полосе запирания [6]. В качестве дефекта может использоваться любой элемент, имеющий электромагнитные свойства отличные от свойств элементов регулярного ЭМК. Важным фактором является также число и расположение дефектов, которые задают форму и размеры резонатора.
В работе [7] исследован один из наиболее простых способов формирования резонатора, при котором изменяется одновременно бесконечный ряд элементов ЭМК. В этом случае резонатор имеет плоско – слоистую структуру. При этом элементы, составляющие дефект выполняются в виде металлических цилиндров с сосредоточенными емкостями. Они формируют резонансную область, в которой происходит накопление энергии. Элементы регулярного ЭМК выполняются в виде однородных металлических цилиндров. Если число рядов регулярного ЭМК конечно, то добротность резонатора также конечна, а ряды металлических цилиндров формируют области связи резонатора с внешней средой.
Важным фактором для
реализации такого типа нелинейного взаимодействия, как генерация кратных
гармоник является особая структура спектра собственных колебаний, в котором
должны существовать собственные колебания с резонансными частотами ![]() , совпадающими с частотами кратными
основной частоте
, совпадающими с частотами кратными
основной частоте ![]() , на которой возбуждается ЭМК.
Спектр колебаний линейного резонатора в ЭМК исследовался в указанной работе
[7]. В ней было показано, что в структурах этого типа возможно создание спектра
колебаний, отвечающего сформулированному выше условию. Данный результат
позволяет рассчитывать на то, что в резонаторах такого типа возможна реализация
сильного эффекта генерации кратных гармоник, при котором существенная доля
энергии возбуждающего сигнала будет преобразована в сигнал на кратной частоте.
Отметим, что в данной работе мы будем рассматривать только наиболее сильный
эффект генерации второй гармоники.
, на которой возбуждается ЭМК.
Спектр колебаний линейного резонатора в ЭМК исследовался в указанной работе
[7]. В ней было показано, что в структурах этого типа возможно создание спектра
колебаний, отвечающего сформулированному выше условию. Данный результат
позволяет рассчитывать на то, что в резонаторах такого типа возможна реализация
сильного эффекта генерации кратных гармоник, при котором существенная доля
энергии возбуждающего сигнала будет преобразована в сигнал на кратной частоте.
Отметим, что в данной работе мы будем рассматривать только наиболее сильный
эффект генерации второй гармоники.
Существенным отличием рассматриваемой в данной работе структуры от исследованной в работе [7] является нелинейность емкостей, формирующих резонансную область. Данный фактор обусловливает необходимость совместного решения граничной электродинамической задачи и нелинейной задачи для токов и напряжений на емкостях. Схема решения и полученные с его помощью результаты представлены ниже.
2. Модель нелинейного резонатора в ЭМК
Исследуемая структура
показана на рис. 1. Она, как отмечалось выше, состоит из решетки металлических
цилиндров. Число цилиндров по оси 0у бесконечно и ограничено по оси 0х.
Внутренняя по оси 0х область формируется цилиндрами с нелинейными емкостями ![]() ,
, ![]() , где
, где ![]() - число слоев в резонансной области.
Области справа и слева от резонансной области имеют
- число слоев в резонансной области.
Области справа и слева от резонансной области имеют ![]() и
и ![]() слоев цилиндров без конденсаторов. Они
выполняют роль областей связи резонатора с внешней схемой.
слоев цилиндров без конденсаторов. Они
выполняют роль областей связи резонатора с внешней схемой.
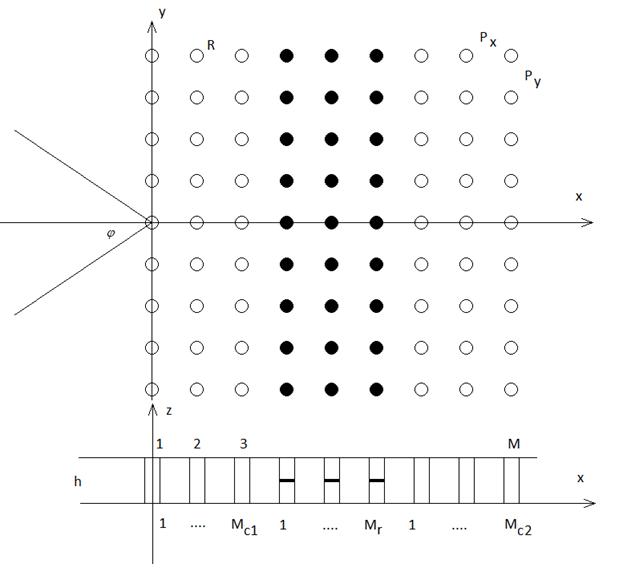
Рис. 1. Исследуемая структура
Для простоты построения
математической модели мы будем считать, что в эти цилиндры также включены
конденсаторы, но их емкости стремятся к бесконечности, а сопротивления
стремятся к нулю. Общее число элементов ЭМК по оси 0х равно ![]() .
.
Роль внешней схемы
выполняет ПВ высотой ![]() , в котором располагается
решетка цилиндров радиуса
, в котором располагается
решетка цилиндров радиуса ![]() . В ПВ распространяется
основная Т - волна, не имеющая частоты отсечки. Наряду с ней при определенных
условиях в ПВ могут распространяться высшие типы волн. Мы предполагаем, что
условия для их распространения отсутствуют как на основной, так и на удвоенной
частотах. Т - волны в нашем случае являются источником возбуждения ЭМК. Пусть для
определенности возбуждающая плоская волна набегает на ЭМК слева (см. рис. 1).
При этом она могут распространяется в плоскости ХОY под углом
. В ПВ распространяется
основная Т - волна, не имеющая частоты отсечки. Наряду с ней при определенных
условиях в ПВ могут распространяться высшие типы волн. Мы предполагаем, что
условия для их распространения отсутствуют как на основной, так и на удвоенной
частотах. Т - волны в нашем случае являются источником возбуждения ЭМК. Пусть для
определенности возбуждающая плоская волна набегает на ЭМК слева (см. рис. 1).
При этом она могут распространяется в плоскости ХОY под углом ![]() относительно оси 0х.
Угол
относительно оси 0х.
Угол ![]() имеет смысл угла падения.
имеет смысл угла падения.
Реакция исследуемой
структуры на возбуждающее воздействие также имеет вид плоских Т - волн ПВ,
бегущих от резонатора. Волны в области ![]() являются
отраженными волнами, а волны в области
являются
отраженными волнами, а волны в области ![]() прошедшими.
Их амплитуды связаны с амплитудой падающей волны через коэффициенты отражения
прошедшими.
Их амплитуды связаны с амплитудой падающей волны через коэффициенты отражения ![]() и прохождения
и прохождения ![]() , где
, где ![]() - номер гармоники основной частоты.
Наличие отраженных и прошедших волн на гармониках основной частоты - следствие нелинейности
структуры.
- номер гармоники основной частоты.
Наличие отраженных и прошедших волн на гармониках основной частоты - следствие нелинейности
структуры.
В резонаторе без тепловых потерь коэффициенты отражения и прохождения удовлетворяют условию энергетического баланса:
Модель представленной выше структуры мало отличается от модели полученной в работе [1]. Поэтому мы не будем подробно рассматривать вывод уравнений, к которым сводится граничная задача для электромагнитного поля, а приведем основные соотношения без вывода:
![]() ,
,
![]() ,
,
где
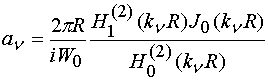 , (3)
, (3)
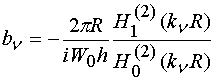 ,
,
![]() ,
,
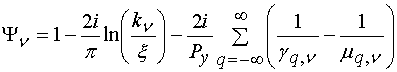 ,
,
![]() ,
, ![]() ,
,
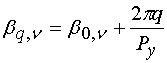 ,
,
![]() ,
, ![]() ,
,
где ![]() -
символ Кронекера,
-
символ Кронекера, ![]() - волновое сопротивление среды
внутри ПВ,
- волновое сопротивление среды
внутри ПВ, ![]() - волновое число свободного пространства
на частоте
- волновое число свободного пространства
на частоте ![]() ,
, ![]() - высота
ПВ,
- высота
ПВ, ![]() - периоды решетки ЭМК,
- периоды решетки ЭМК, ![]() - номер максимальной гармоники основной
частоты, учитываемой в решении,
- номер максимальной гармоники основной
частоты, учитываемой в решении, ![]() - номер гармоники
основной частоты,
- номер гармоники
основной частоты, ![]() - функция Бесселя нулевого
порядка,
- функция Бесселя нулевого
порядка, ![]() - функции Ганкеля второго рода нулевого и
первого порядков. Индексы
- функции Ганкеля второго рода нулевого и
первого порядков. Индексы ![]() описывают положение
элемента ЭМК по оси 0х. Вектора
описывают положение
элемента ЭМК по оси 0х. Вектора ![]() и
и ![]() имеют размерность равную
имеют размерность равную ![]() . Их элементами соответственно являются
токи, текущие по цилиндрам ЭМК и напряжения на нелинейных емкостях. Вектор
. Их элементами соответственно являются
токи, текущие по цилиндрам ЭМК и напряжения на нелинейных емкостях. Вектор ![]() имеет такую же размерность, а его
элементами являются напряженности компоненты поля
имеет такую же размерность, а его
элементами являются напряженности компоненты поля ![]() падающей
волны в центрах цилиндров ЭМК. При выводе соотношений (2) – (4) принято во
внимание, что в силу периодичности ЭМК по оси 0у все электродинамические
параметры имеют экспоненциальную зависимость от индекса
падающей
волны в центрах цилиндров ЭМК. При выводе соотношений (2) – (4) принято во
внимание, что в силу периодичности ЭМК по оси 0у все электродинамические
параметры имеют экспоненциальную зависимость от индекса ![]() :
:
![]() .
.
Индекс ![]() описывает
положение центра элемента ЭМК по оси 0у. Волновое число
описывает
положение центра элемента ЭМК по оси 0у. Волновое число ![]() задается
падающей волной, поле которой описывается следующим образом:
задается
падающей волной, поле которой описывается следующим образом:
![]() ,
,
![]() ,
,
![]() - амплитуда электрического поля падающей волны.
Полезно также ввести напряжение падающей волны
- амплитуда электрического поля падающей волны.
Полезно также ввести напряжение падающей волны ![]() .
.
В уравнении (2) под ![]() понимается нелинейный оператор, связывающий гармоники тока с гармониками
напряжения на нелинейных емкостях. В общем случае он имеет следующий вид:
понимается нелинейный оператор, связывающий гармоники тока с гармониками
напряжения на нелинейных емкостях. В общем случае он имеет следующий вид:
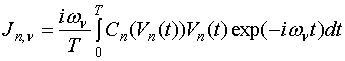 , (5)
, (5)
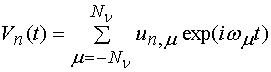 ,
,
где ![]() ,
, ![]() - емкости конденсаторов, зависящие в
общем случае от напряжения. Целесообразно также ввести конденсаторы в
резонансной области
- емкости конденсаторов, зависящие в
общем случае от напряжения. Целесообразно также ввести конденсаторы в
резонансной области ![]() ,
, ![]() .
.
Благодаря оператору ![]() система уравнений (2) становится
нелинейной системой, которую в общем случае можно решить только численными
методами. В данной работе для ее решения использовался метод последовательных
приближений. В качестве нулевого приближения бралось решение линейной задачи
при
система уравнений (2) становится
нелинейной системой, которую в общем случае можно решить только численными
методами. В данной работе для ее решения использовался метод последовательных
приближений. В качестве нулевого приближения бралось решение линейной задачи
при ![]() .
.
Зависимость емкости от напряжения бралась нами в следующем виде:
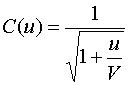 . (6)
. (6)
Соотношение (6) соответствует
зависимости емкости от напряжения СВЧ полупроводникового диода [8], ![]() - напряжение пробоя диода. При анализе
рассматриваемой структуры мы предполагали, что на конденсаторы может подаваться
постоянное напряжение смещение
- напряжение пробоя диода. При анализе
рассматриваемой структуры мы предполагали, что на конденсаторы может подаваться
постоянное напряжение смещение ![]() , задающее рабочую
точку диода.
, задающее рабочую
точку диода.
Отличие модели представленной выше от модели из работы [1] только в том, что теперь мы предполагаем, что конденсаторы, включенные в разные элементы ЭМК имеют разные емкости.
3. Резонатор с двумя входами
Все представленные ниже
численные результаты получены для резонатора, имеющего три активных слоя (![]() ). Он исследовался в двух вариантах: с
одним и двумя входами. Число входов определяется параметрами двух областей
связи:
). Он исследовался в двух вариантах: с
одним и двумя входами. Число входов определяется параметрами двух областей
связи: ![]() и
и ![]() .
Увеличивая один из указанных параметров, например,
.
Увеличивая один из указанных параметров, например, ![]() , можно
уменьшить связь с правой стороны резонатора до нуля. В этом случае резонатор
взаимодействует только с ПВ при
, можно
уменьшить связь с правой стороны резонатора до нуля. В этом случае резонатор
взаимодействует только с ПВ при ![]() , что с точки зрения
теории цепей СВЧ эквивалентно наличию у него одного входа. В этом случае его
можно рассматривать как двухполюсник. Коэффициенты прохождения
, что с точки зрения
теории цепей СВЧ эквивалентно наличию у него одного входа. В этом случае его
можно рассматривать как двухполюсник. Коэффициенты прохождения ![]() тогда равны нулю.
тогда равны нулю.
Если оба параметра ![]() и
и ![]() таковы,
что взаимодействие резонатора идет как с ПВ при
таковы,
что взаимодействие резонатора идет как с ПВ при ![]() , так и
с ПВ при
, так и
с ПВ при ![]() , то его можно рассматривать как СВЧ
четырехполюсник с двумя входами.
, то его можно рассматривать как СВЧ
четырехполюсник с двумя входами.
Ряд параметров во всех
численных экспериментах оставался неизменным. Перечислим их: ![]() ,
, ![]() ,
, ![]() В,
В, ![]() В,
В, ![]() пФ,
пФ, ![]() ,
, ![]() В. Напомним, что
В. Напомним, что ![]() ,
,
![]() - напряжения смещения на конденсаторах в
резонансной области. Они задают среднее значение емкости. Резонатор с двумя
входами имеет
- напряжения смещения на конденсаторах в
резонансной области. Они задают среднее значение емкости. Резонатор с двумя
входами имеет ![]() . У резонатора с одним входом
. У резонатора с одним входом ![]() . Все геометрические размеры здесь и далее
приводятся в миллиметрах.
. Все геометрические размеры здесь и далее
приводятся в миллиметрах.
В ходе численных расчетов
исследовалось влияние на структуру переменных параметров: напряжения падающей
волны ![]() , угла падения
, угла падения ![]() ,
расстройки резонансных частот
,
расстройки резонансных частот ![]() , добротности
резонатора
, добротности
резонатора ![]() . Расстройка
. Расстройка ![]() определяется
следующим образом:
определяется
следующим образом:
![]() . (7)
. (7)
Видно, что при ![]() имеются оптимальные условия для генерации
второй гармоники, если резонатор возбуждается сигналом с частотой
имеются оптимальные условия для генерации
второй гармоники, если резонатор возбуждается сигналом с частотой ![]() .
.
Для количественной оценки
эффективности генерации второй гармоники удобно ввести коэффициенты ![]() :
:
![]() , (8)
, (8)
![]() .
.
Отметим, что все параметры ![]() ,
,![]() пренебрежимо
малы при
пренебрежимо
малы при ![]() . В этом случае коэффициент
. В этом случае коэффициент ![]() показывает какая часть энергии падающей
волны преобразовалась в энергию волн на второй гармонике основной частоты, а
коэффициент
показывает какая часть энергии падающей
волны преобразовалась в энергию волн на второй гармонике основной частоты, а
коэффициент ![]() равен части энергии падающей волны,
которая осталась на основной частоте.
равен части энергии падающей волны,
которая осталась на основной частоте.
Рассмотрим влияние на
функционирование структуры интенсивности падающей волны. Исследуемый резонатор
настроен в режим синхронизма с ![]() для угла падения
для угла падения ![]() . Структура имеет следующие переменные
параметры:
. Структура имеет следующие переменные
параметры: ![]() В,
В, ![]() ,
, ![]() .
.
На рис. 2 показана частотная
зависимость коэффициентов ![]() . Кривые 1 - 3
соответствуют
. Кривые 1 - 3
соответствуют ![]() , а кривые 1' - 3' соответствуют
, а кривые 1' - 3' соответствуют
![]() . Они получены для
. Они получены для ![]() и
и
![]() В.
В.
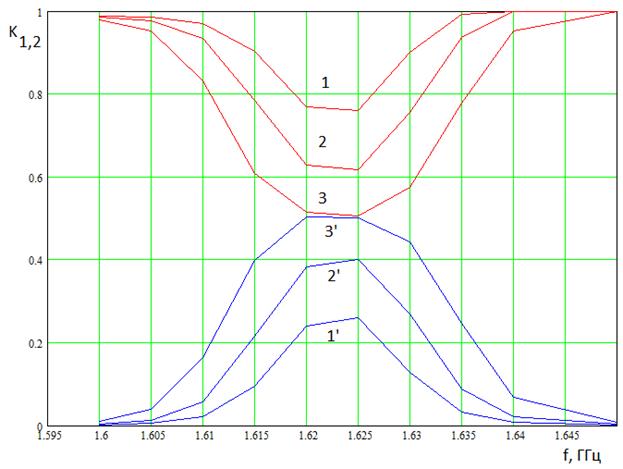
Рис. 2. Частотная зависимость
коэффициентов ![]() при
при ![]()
Видно, что частотная
зависимость коэффициентов ![]() имеет типичный
резонансный характер. Центральная частота находится вблизи 1.625 ГГц. Сумма
параметров
имеет типичный
резонансный характер. Центральная частота находится вблизи 1.625 ГГц. Сумма
параметров ![]() равна единице, что следует из уравнения
энергетического баланса (1).
равна единице, что следует из уравнения
энергетического баланса (1).
При увеличении мощности
падающей волны наблюдается рост коэффициента ![]() и
уменьшение
и
уменьшение ![]() . На центральной частоте параметр
. На центральной частоте параметр ![]() растет до величины 0.5. Исследовать
поведение структуры при дальнейшем увеличении напряжения
растет до величины 0.5. Исследовать
поведение структуры при дальнейшем увеличении напряжения ![]() с помощью модели описанной выше оказалось
невозможным, так как после достижении значения
с помощью модели описанной выше оказалось
невозможным, так как после достижении значения ![]() итерационная
процедура решения системы нелинейных уравнений расходится.
итерационная
процедура решения системы нелинейных уравнений расходится.
Расходимость итерационных методов общего вида при описании нелинейных систем в режимах накопления является типичной ситуацией, которая описана, например, в работе [3]. Для преодоления этой сложности необходимо разработать специализированную модель, в которой путем специальных аналитических преобразований учитываются особенности пространственного синхронизма или возбуждения высокодобротных колебаний. Такая модель была разработана нами. С ее помощью возможно исследовать резонаторы, возбуждаемые волнами произвольной интенсивности. Однако ее описание выходят за рамки данной работы.
Таким образом, в рамках
прямого численного решения системы нелинейных уравнений вопрос о возможности
реализации структур с ![]() остается открытым. Забегая
несколько вперед, мы отметим, что аналитическая модель позволяет положительно
ответить на поставленный выше вопрос: создание таких структур возможно, однако,
превышение параметра
остается открытым. Забегая
несколько вперед, мы отметим, что аналитическая модель позволяет положительно
ответить на поставленный выше вопрос: создание таких структур возможно, однако,
превышение параметра ![]() над уровнем 0.5 незначительно.
На рис. 3 показана частотная зависимость коэффициента
над уровнем 0.5 незначительно.
На рис. 3 показана частотная зависимость коэффициента ![]() ,
полученная для резонатора, настроенного в синхронизма при
,
полученная для резонатора, настроенного в синхронизма при ![]() . Кривые 1 - 3 получены при
. Кривые 1 - 3 получены при ![]() при
при ![]() В,
В, ![]() ,
, ![]() .
.
Видно, что кривые 2 и 3 продолжены выше уровня 0.5 с помощью упомянутой выше аналитической модели. Однако, даже в максимуме они не превышают значения 0.53.
В кривых на рис.2,3 обращает
на себя внимание то, что с ростом напряжения падающей волны растет не только
интенсивность генерации второй гармоники, но и ширина кривой. Обычно расширение
резонансной кривой связывают со снижением добротности резонатора. В нашем
случае такое предположение некорректно, так как связь резонатора с внешней
схемой фиксирована. Она не зависит от напряжения ![]() .
.
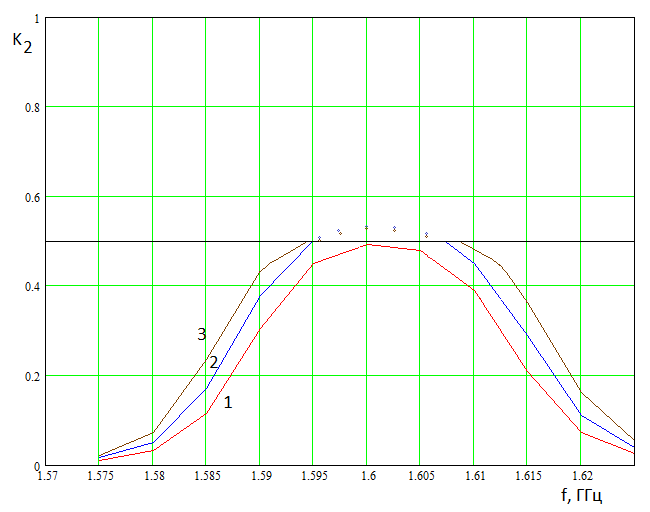
Рис. 3. Частотная зависимость
коэффициента ![]() при
при ![]()
Таким образом кривая
расширяется без снижения добротности. Можно предположить, что причина данного
эффекта связана с другим явлением. Точно условия синхронизма соблюдаются в
линейном режиме в котором параметр ![]() практически равен
нулю. Однако, в нелинейном режиме колебания резонатора связываются друг с
другом за счет нелинейности емкостей. Данная связь эквивалентна тому, что в
контур вносится дополнительная реактивность, которая смещает резонансные
частоты таким образом, что параметр
практически равен
нулю. Однако, в нелинейном режиме колебания резонатора связываются друг с
другом за счет нелинейности емкостей. Данная связь эквивалентна тому, что в
контур вносится дополнительная реактивность, которая смещает резонансные
частоты таким образом, что параметр ![]() уже не равен нулю.
Расхождение резонансных частот приводит к расширению кривых.
уже не равен нулю.
Расхождение резонансных частот приводит к расширению кривых.
Таким образом, в
рассматриваемой структуре при увеличении интенсивности падающей волны действуют
два противоречивых фактора. С одной стороны, генерация второй гармоники
увеличивается из-за роста напряжения волны, а с другой стороны, она уменьшается
из-за нарушения условия синхронизма. В таких случаях всегда следует ожидать
экстремальной зависимости рассматриваемого параметра, в данном случае ![]() . Абсолютное его значение в точке
максимума, как видно из рис. 3 близко к 0.5.
. Абсолютное его значение в точке
максимума, как видно из рис. 3 близко к 0.5.
Частотная зависимость
коэффициента ![]() при настройке на нулевой угол падения
мало отличается от представленной на рис. 2. Это видно из рис. 4, на котором
показаны зависимости
при настройке на нулевой угол падения
мало отличается от представленной на рис. 2. Это видно из рис. 4, на котором
показаны зависимости ![]() и
и ![]() от
частоты. Кривые 1,2 соответствуют
от
частоты. Кривые 1,2 соответствуют ![]() , а кривые 1',2'
параметру
, а кривые 1',2'
параметру ![]() . Они получены при
. Они получены при ![]() соответственно.
На кривой 2 видно срезанное основание, а на кривой 2' срезанная вершина. Это
означает, что в этой области параметров завершить расчет не удалось из-за
расходимости решения.
соответственно.
На кривой 2 видно срезанное основание, а на кривой 2' срезанная вершина. Это
означает, что в этой области параметров завершить расчет не удалось из-за
расходимости решения.
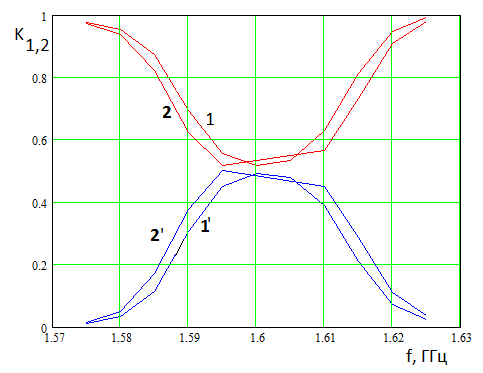
Рис.4. Частотная зависимость коэффициентов ![]() при
при ![]()
Рассмотрим
далее зависимость параметров ![]() от угла падения
от угла падения ![]() .
.
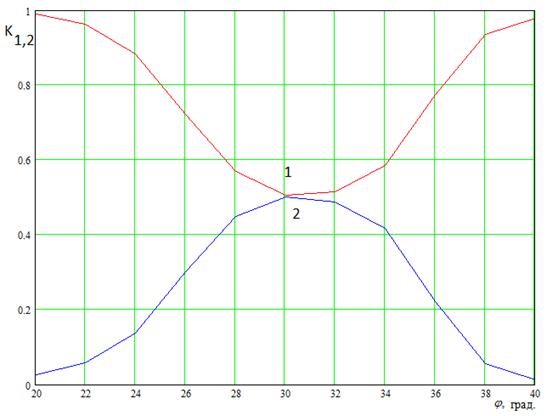
Рис. 5. Зависимость коэффициентов ![]() от угла падения
от угла падения
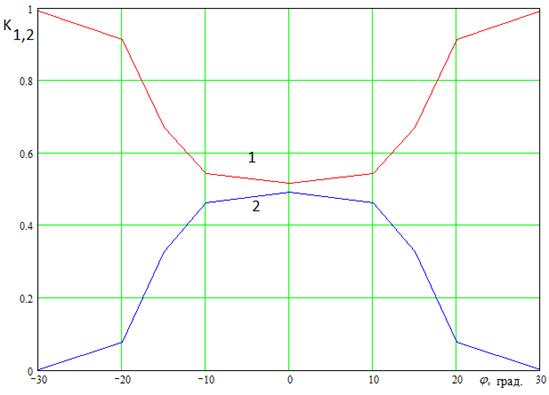
Рис. 6. Зависимость коэффициентов ![]() от угла падения
от угла падения
На рис. 5 показаны такие
зависимости при настройке резонатора на угол ![]() , а на
рис. 6 при настройке на нулевой угол падения. Параметры структуры,
обеспечивающие синхронизм при указанных выше углах, остались без изменения. Они
приведены выше.
, а на
рис. 6 при настройке на нулевой угол падения. Параметры структуры,
обеспечивающие синхронизм при указанных выше углах, остались без изменения. Они
приведены выше.
Видно, что кривые на рис. 5
значительно уже кривых на рис. 6. Более сильное влияние угла падения при
настройке на угол отличный от нуля объясняется тем, что зависимость
коэффициентов ![]() от угла
от угла ![]() должна
быть четной. Этот вывод следует из симметрии структуры относительно оси 0х.
Поэтому в окрестности точки
должна
быть четной. Этот вывод следует из симметрии структуры относительно оси 0х.
Поэтому в окрестности точки ![]() первые производные
функций
первые производные
функций ![]() равны нулю и отклонение угла падения
меняет указанные функции лишь во втором порядке малости. Наоборот, при
равны нулю и отклонение угла падения
меняет указанные функции лишь во втором порядке малости. Наоборот, при ![]() влияние угла на функции
влияние угла на функции ![]() идет уже в первом порядке малости.
идет уже в первом порядке малости.
Интересно исследовать влияние
на эффект генерации второй гармоники точности выполнения условия синхронизма. С
этой целью будем менять напряжение на втором конденсаторе ![]() . При этом одновременно изменяем угол
падения
. При этом одновременно изменяем угол
падения ![]() таким образом, чтобы частота
таким образом, чтобы частота ![]() оставалась постоянной, а варьировалась
только частота
оставалась постоянной, а варьировалась
только частота ![]() . При этом расстройка
. При этом расстройка ![]() будет меняться благодаря изменению
частоты
будет меняться благодаря изменению
частоты ![]() . Первый рассмотренный случай
соответствует смещению вверх частоты
. Первый рассмотренный случай
соответствует смещению вверх частоты ![]() относительно удвоенной
частоты
относительно удвоенной
частоты ![]() .
.
Частотная зависимость
параметров ![]() показана на рис. 7. Кривая 1 соответствует
показана на рис. 7. Кривая 1 соответствует
![]() , а кривая 2 коэффициенту
, а кривая 2 коэффициенту ![]() . Они получены при следующих параметрах:
. Они получены при следующих параметрах: ![]() МГц,
МГц, ![]() В,
В, ![]() ,
, ![]() ГГц.
ГГц.
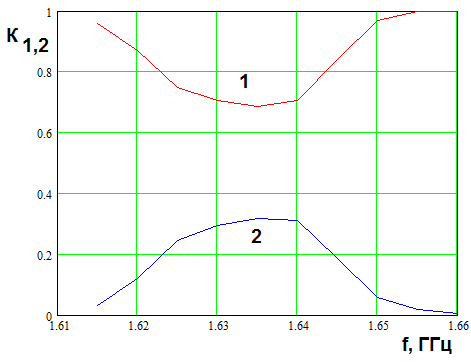
Рис. 7. Частотная зависимость
коэффициентов ![]() при расстройке резонансных
частот
при расстройке резонансных
частот
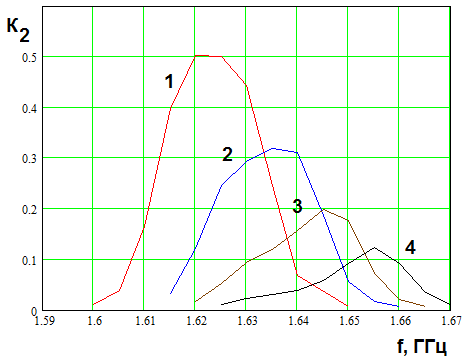
Рис. 8. Частотная зависимость
коэффициента ![]() при смещении частоты
при смещении частоты ![]() вверх
вверх
На рис. 8 показана частотная
зависимость коэффициента ![]() . Кривые 1 - 4
соответствуют
. Кривые 1 - 4
соответствуют ![]() МГц,
МГц, ![]() В,
В,
![]() ,
, ![]() ГГц.
Видно, что при увеличении расстройки
ГГц.
Видно, что при увеличении расстройки ![]() эффективность
генерации второй гармоники падает. При этом кривая частотной зависимости
параметра
эффективность
генерации второй гармоники падает. При этом кривая частотной зависимости
параметра ![]() расширяется. Максимум коэффициент
расширяется. Максимум коэффициент ![]() достигает в окрестности частоты
достигает в окрестности частоты ![]() .
.
Аналогично ведут себя
коэффициенты ![]() при смещении частоты
при смещении частоты ![]() вниз относительно удвоенной частоты
вниз относительно удвоенной частоты ![]() . На рис. 9 показана частотная зависимость
параметра
. На рис. 9 показана частотная зависимость
параметра ![]() . Кривые 1 - 4 соответствуют
. Кривые 1 - 4 соответствуют ![]() МГц. Они получены для
МГц. Они получены для ![]() В,
В, ![]() ,
, ![]() ГГц,
ГГц, ![]() ГГц.
ГГц.
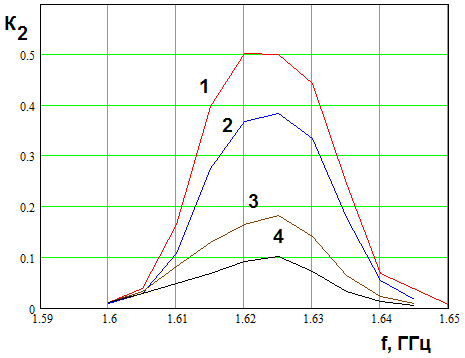
Рис. 9. Частотная зависимость
коэффициента ![]() при смещении частоты
при смещении частоты ![]() вниз
вниз
Важным параметром резонатора
является его добротность. Рассмотрим как изменение добротности влияет на эффект
генерации второй гармоники. В рассматриваемой структуре тепловые потери не
учитываются. Поэтому резонатор имеет конечную добротность исключительно
вследствие его связи с внешней схемой, то есть с волнами ПВ. Поэтому для
изменения добротности необходимо изменить условия связи резонатора с ПВ. Связь
определяется числом цилиндров в области связи и их радиусом ![]() . Использование параметров
. Использование параметров ![]() для регулировки связи с внешней схемой
неудобно, так как она очень сильно зависит от числа цилиндров. Для плавного
изменения связи удобнее использовать радиус
для регулировки связи с внешней схемой
неудобно, так как она очень сильно зависит от числа цилиндров. Для плавного
изменения связи удобнее использовать радиус ![]() .
.
Изменение радиуса цилиндров
приводит к изменению частот ![]() и нарушению условия
синхронизма. Поэтому одновременно с изменением радиуса
и нарушению условия
синхронизма. Поэтому одновременно с изменением радиуса ![]() приходится
менять такие параметры, как период
приходится
менять такие параметры, как период ![]() и напряжение
и напряжение ![]() . Изменения указанных параметров
проводились таким образом, чтобы частота
. Изменения указанных параметров
проводились таким образом, чтобы частота ![]() оставалась
постоянной и равной 1.625 ГГц и выполнялось равенство
оставалась
постоянной и равной 1.625 ГГц и выполнялось равенство ![]() .
.
На рис. 10 показана частотная
зависимость коэффициента ![]() . Кривые 1 - 3 получены
для
. Кривые 1 - 3 получены
для ![]() ,
, ![]() ,
, ![]() В,
В, ![]() ,
, ![]() В. Видно, что изменение добротности,
которая повышается с ростом радиуса
В. Видно, что изменение добротности,
которая повышается с ростом радиуса ![]() , приводит к ожидаемому сужению
кривой. Однако, при этом в максимуме значение параметра
, приводит к ожидаемому сужению
кривой. Однако, при этом в максимуме значение параметра ![]() с
ростом добротности не меняется и остается приблизительно равным 0.5.
с
ростом добротности не меняется и остается приблизительно равным 0.5.
Таким образом, из исследования резонатора с двумя входами можно сделать вывод о том, что в этой структуре имеется ограничение на эффективность генерации второй гармоники, препятствующее преобразованию более половины мощности сигнала основной частоты в сигнал удвоенной частоты.
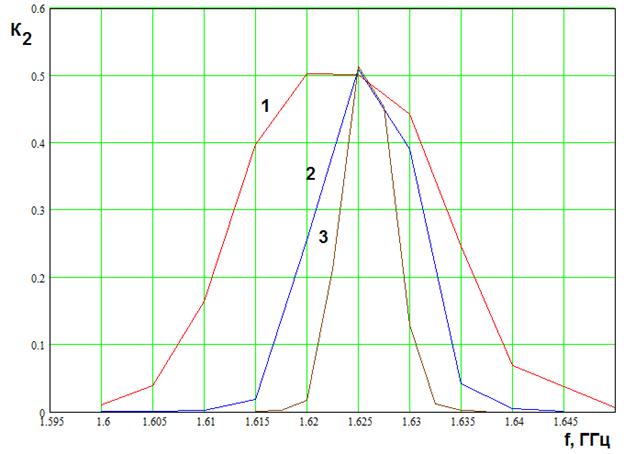
Рис. 10. Частотная зависимость
коэффициента ![]() при разной добротности резонатора
при разной добротности резонатора
4. Резонатор с одним входом
Рассмотрим далее резонатор с
одним входом. Для этого увеличим параметр ![]() ,
сделав его равным трем. Будем исследовать зависимость генерации второй
гармоники только от напряжения падающей волны, поскольку ее зависимость от
других параметров аналогична рассмотренным в разд. 3. Резонатор с одним входом
имел следующие параметры:
,
сделав его равным трем. Будем исследовать зависимость генерации второй
гармоники только от напряжения падающей волны, поскольку ее зависимость от
других параметров аналогична рассмотренным в разд. 3. Резонатор с одним входом
имел следующие параметры: ![]() ,
, ![]() ,
, ![]() ,
, ![]() В,
В, ![]() .
.
На рис. 11 показана частотная
зависимость коэффициентов ![]() . Кривая 1 соответствует параметру
. Кривая 1 соответствует параметру ![]() , а кривая 2 -
, а кривая 2 - ![]() . Они
получены для напряжения падающей волны
. Они
получены для напряжения падающей волны ![]() В.
В.
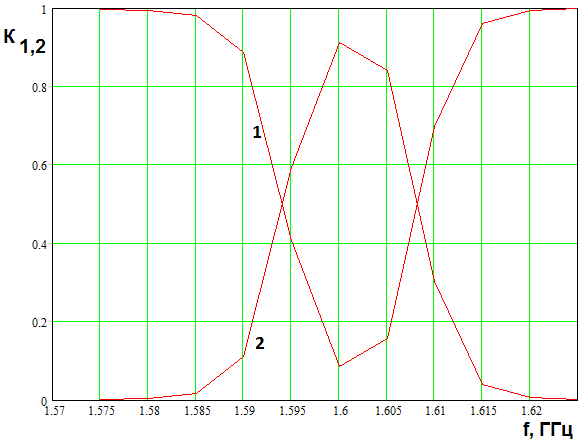
Рис. 11. Частотная зависимость
коэффициентов ![]() для резонатора с одним входом
для резонатора с одним входом
Обращает на себя внимание то,
что при напряжении падающей волны 0.006 максимальное значение коэффициента ![]() не только существенно больше, чем у
резонатора с двумя входами, но оно превышает значение 0.9. Таким образом, мы
можем сделать вывод о том, что ограничение на эффективность генерации второй
гармоники характерное для резонатора с двумя входами в одновходовом резонаторе
снимается. В принципе в нем возможно полное преобразовании энергии волны
основной частоты в волну удвоенной частоты.
не только существенно больше, чем у
резонатора с двумя входами, но оно превышает значение 0.9. Таким образом, мы
можем сделать вывод о том, что ограничение на эффективность генерации второй
гармоники характерное для резонатора с двумя входами в одновходовом резонаторе
снимается. В принципе в нем возможно полное преобразовании энергии волны
основной частоты в волну удвоенной частоты.
На рис. 12 показана частотная
зависимость параметра ![]() . Кривые 1 - 3 получены для
. Кривые 1 - 3 получены для ![]() В. остальные параметры остались
неизменными.
В. остальные параметры остались
неизменными.
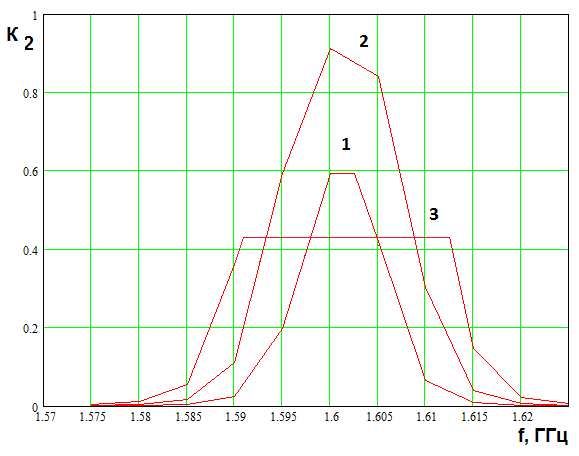
Рис. 12. Частотная зависимость
коэффициента ![]() для резонатора с одним входом
для резонатора с одним входом
Срезанная вершина у кривой 3
говорит о том, что на этих частотах итерационный процесс для данной
совокупности параметров разошелся. Аналогично резонатору с двумя входами мы
наблюдаем расширение кривой частотной зависимости коэффициента ![]() при увеличении напряжения падающей волны.
при увеличении напряжения падающей волны.
5. Качественная модель резонаторов с одним и двумя входами
Численное исследование генерации второй гармоники в резонаторах на основе ЭМК, результаты к которого представлены выше показало важное отличие между схемой с одним и двумя входами. Его можно качественно объяснить с помощью модели, которую мы обсудим в данном разделе. При этом мы не ставим цель получить с ее помощью достоверные количественные результаты. Наша задача состоит в том, чтобы найти причину существенного отличия между двумя структурами.
На рис. 13 а,б показаны две эквивалентные схемы, с помощью которых мы можем качественно исследовать резонаторы с одним и двумя входами.
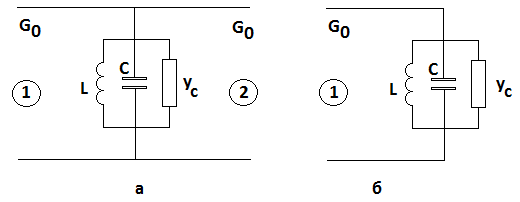
Рис. 13. Эквивалентные схемы резонаторов с двумя и одним входами на основной частоте
Схема на рис. 13 а
соответствует резонатору с двумя входами, а схема на рис. 13 б с одним входом.
Схемы имеют параллельный контур, который моделирует реальный резонатор с
колебанием на частоте ![]() . Контура включены в линию
передачи в характеристической проводимостью
. Контура включены в линию
передачи в характеристической проводимостью ![]() . Она
служит моделью ПВ. Контур в схеме на рис. 13 а включен в линию передачи в виде
параллельной нагрузки. Таким образом, вся схема представляет собой СВЧ
четырехполюсник с двумя входами. Контур в семе на рис. 13 б включен в линию
передачи в виде оконечной нагрузки, которая является СВЧ двухполюсником.
. Она
служит моделью ПВ. Контур в схеме на рис. 13 а включен в линию передачи в виде
параллельной нагрузки. Таким образом, вся схема представляет собой СВЧ
четырехполюсник с двумя входами. Контур в семе на рис. 13 б включен в линию
передачи в виде оконечной нагрузки, которая является СВЧ двухполюсником.
Контура содержат кроме ![]() элементов, настроенных на частоту
элементов, настроенных на частоту ![]() дополнительную проводимость
дополнительную проводимость ![]() . Появление этой проводимости обусловлено
нелинейным взаимодействием. Активная часть проводимости
. Появление этой проводимости обусловлено
нелинейным взаимодействием. Активная часть проводимости ![]() отражает
потери мощности сигнала основной частоты, который преобразуется в сигнал на
удвоенной частоте. Мнимая часть проводимости
отражает
потери мощности сигнала основной частоты, который преобразуется в сигнал на
удвоенной частоте. Мнимая часть проводимости ![]() соответствует
реактивной проводимости вносимой в контур вследствие возбуждения колебаний в
контуре на частоте
соответствует
реактивной проводимости вносимой в контур вследствие возбуждения колебаний в
контуре на частоте ![]() .
.
Очевидно, что все элементы схем на рис. 13 а,б остаются неопределенными, так как их связь с параметрами реальной структуры неизвестна. Однако, мы можем исследовать зависимость выходных характеристик эквивалентных схем от их параметров и найти причину отличия между схемой с одним и двумя входами.
Не составляет труда найти
элементы матрицы рассеяния эквивалентных схем. Для схемы на рис. 13 а это будут
коэффициент отражения ![]() и коэффициент прохождения
и коэффициент прохождения ![]() . Для схемы на рис. 13 б матрица рассеяния
имеет один коэффициент отражения
. Для схемы на рис. 13 б матрица рассеяния
имеет один коэффициент отражения ![]() . Индекс 1 показывает,
что матрица рассеяния ищется на основной частоте.
. Индекс 1 показывает,
что матрица рассеяния ищется на основной частоте.
Указанные выше параметры выражаются следующим образом:
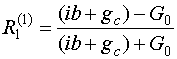 ,
,
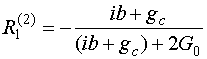 , (9)
, (9)
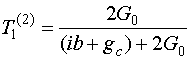 ,
,
где
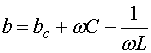 ,
,
![]() -
круговая частота. Верхний индекс в соотношениях (9) соответствует числу входов
схемы.
-
круговая частота. Верхний индекс в соотношениях (9) соответствует числу входов
схемы.
С помощью параметров рассеяния
(9) не составляет труда найти коэффициент ![]() :
:
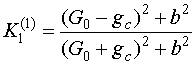 , (10)
, (10)
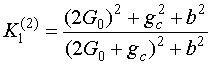 .
.
Чтобы найти наиболее
интересный для нас коэффициент ![]() воспользуемся законом
сохранения энергии (1), полагая, что в структуре существуют сигналы только на
основной и удвоенной частотах:
воспользуемся законом
сохранения энергии (1), полагая, что в структуре существуют сигналы только на
основной и удвоенной частотах:
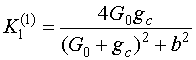 , (11)
, (11)
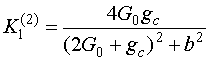 .
.
При увеличении напряжения
возбуждающего сигнала, как отмечалось выше, интенсивность нелинейного
взаимодействия растет. Это находит отражение в росте проводимости ![]() . Таким образом, мы можем исследовать
зависимость коэффициента
. Таким образом, мы можем исследовать
зависимость коэффициента ![]() от проводимости
от проводимости ![]() и считать, что качественно она совпадает
с зависимостью данного параметра от напряжения падающей волны.
и считать, что качественно она совпадает
с зависимостью данного параметра от напряжения падающей волны.
Из формул (11) следует, что
обе функции имеют максимум по аргументу ![]() .
Значение аргумента в точке максимума дает нам оптимальное значение
проводимости:
.
Значение аргумента в точке максимума дает нам оптимальное значение
проводимости:
![]() , (12)
, (12)
![]() ,
,
![]() .
.
При этом максимальные значения
параметра ![]() выражаются следующим образом:
выражаются следующим образом:
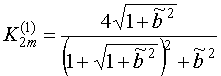 , (13)
, (13)
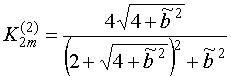 .
.
Из соотношений видно, что
абсолютного максимума коэффициенты ![]() достигают при
достигают при ![]() . При
этом
. При
этом
![]() ,
, ![]() . (14)
. (14)
Таким образом, качественная модель дала нам результат, совпадающий с численным решением. Следовательно, ограничения эффективности генерации второй гармоники в резонаторе с двумя входами не связаны с конкретной структурой ЭМК и ее параметрами. Они обусловлены только наличием двух входов. Можно сделать вывод, что второй вход является дополнительным источником потерь для колебания, резонирующего вблизи основной частоты. Эти потери не позволяют преобразовать в сигнал удвоенной частоты более половины мощности источника возбуждения.
Отметим, что данное ограничение, как следует из качественной модели, должно сниматься если резонатор с двумя входами возбуждать одновременно с двух сторон. В этом случае в силу симметрии он будет эквивалентен резонатору с одним входом.
Работа выполнена при поддержке Российского фонда фундаментальных исследований. Проект № 11-08-00215-а.
1. Банков С.Е. Модель нелинейного электромагнитного кристалла // РЭ. 2011. Т.56. №3. С. 261.
2. Банков С.Е. Полубесконечный нелинейный электромагнитный кристалл // РЭ. 2011. Т.56. №5. С. 1-11.
3. Банков С.Е. Взаимодействие прямых волн в нелинейном электромагнитном кристалле // Журнал радиоэлектроники. 2011. №3. http://jre.cplire.ru/jre/mar11/1/text.html.
4. Банков С.Е. Численное исследование взаимодействия прямой и обратной волн в нелинейном электромагнитном кристалле // Успехи современной радиоэлектроники. 2011. №5. С. 31-43.
5. Банков С.Е. Аналитическое исследование двухчастотного взаимодействия прямой и обратной волн в нелинейном электромагнитном кристалле // РЭ. 2011. Т.56. №8. С. 909-919.
6. Банков С.Е. Электромагнитные кристаллы. М.: Физматлит. 2010. 352 С.
7. Банков С.Е., Дупленкова М.Д., Фролова Е.В.
8. Гупта К., Гардж Р., Чадха Р. Машинное проектирование СВЧ устройств. М.: Радио и связь. 1987.