УДК 621.396

Исследование влияния количества уровней дискретизации размытого изображения на качество восстановления

 

А. Ю. Зражевский, А. В. Кокошкин, В. А. Коротков

ИРЭ им. В.А.Котельникова РАН,  Фрязинский филиал

Получена 2 сентября 2013 г.

Аннотация.  Качество изображений, при количестве уровней дискретизации уровней яркости 256 (наиболее распространённое) или 128 и даже 64 уровня,  визуально практически не отличимы человеком друг от друга.  Однако, при попытках улучшения качества изображений различными численными методами, большое значение имеют ошибки, возникающие при оцифровке (дискретизации) аналогового сигнала. Это важно при проектировании систем радиовидения. При записи для сохранения изображений возможно снижение  качества измерений из-за отбрасывания «избыточной» точности, с точки зрения первичной визуализации. Целью данной работы является выяснение влияния шума вызванного квантованием яркости изображения на процесс повышения качества изображений.

Ключевые слова: шум дискретизации, восстановление изображений.

Abstract :  The difference in image quality is almost not distinguishable by human being if 256 (the most common) or 128 and even 64 brightness levels are used. However, errors due to discretization of analog signal play a significant role in improvement of image quality. The latter is important in constructing radio-vision systems. The image quality can be decreased after saving it on a disk due to dropping of an excessive (at first glance) accuracy. The purpose of this paper is investigation of the influence of the noise produced by discretization of brightness on the process of the improvement of the image quality.

Key words: discretization noise, image restoration.

 

В нашей работе [1] рассматривался метод инверсной фильтрации для восстановления изображений с учетом квантования яркости при записи в BMP файл.

         В спектральном виде формирование спектра изображения происходит согласно формуле:

,                                                    (1)

где  и  соответствуют пространственным спектрам соответственно изображения и объекта, а  - спектр аппаратной функции. В силу того, что оптическая система имеет конечную апертуру  отличен от нуля только в определенной области малых пространственных частот. Поэтому формирование изображения соответствует случаю низкочастотной фильтрации исходного сигнала. Уменьшению размеров области пропускания оптической системой способствуют как несовершенство самой оптической системы, так и условия формирования и фиксации изображения. Например, если  имеет вид функции Гаусса, то спектр  в значительной мере будет определяться именно видом  и будет похож на функцию Гаусса

,                                                      (2)

где - среднеквадратичное отклонение.

Если мы хотим по известным  и  определить , то логично воспользоваться инверсной фильтрацией:

.                                                                  (3)

         Однако спектр изображения  известен с конечной точностью, определяемой количеством уровней квантования яркости. Поэтому при малых значениях спектра  ошибки в вычислении  из (3) будут большие и не позволят восстановить изображение из такого спектра . Поэтому в [1] рассмотрен метод восстановления изображения, основанный на использовании в качестве априорной информации предположения о характере доминирующего шума, вызванного квантованием яркости изображения, что позволяет правильно выделить спектральную область, содержащую этот шум, приравнять нулю все амплитуды пространственных гармоник спектра в этой области, а затем, с помощью инверсной фильтрации, восстановить изображение. Определить пространственные частоты, на которых преобладает шум предлагается с помощью условия:

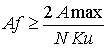,                                                                                 (4)

где - спектральная амплитуда для данной пространственной частоты, - максимальная яркость изображения (для BMP файла ), - количество пикселов изображения по горизонтали (вертикали), - количество уровней дискретизации яркости (для BMP файла ). При не выполнении условия (4) на данной частоте шум квантования яркости доминирует.

         Рассмотрим влияние количества уровней дискретизации яркости на качество восстановления изображения на примере изображения, отфильтрованного с помощью фильтра Гаусса (2). Исходное и отфильтрованное (размытое) изображения представлены на Рис.1.

 

           

а                                                       б

Рис.1 Исходное – а и размытое – б по Гауссу при S=6 изображение.

 

         

а                                                       б

Рис.2 Размытое Гауссом при S=6 – а и восстановленное изображения – б,
количество уровней дискретизации 256.

 

Следующие рисунки иллюстрируют, как работает опубликованный в  [1] метод при разных количествах уровней дискретизации.

 

Рис.3 Размытое Гауссом при S=6 – а и восстановленное изображения – б,
количество уровней дискретизации 128.

 

а                                                       б

Рис.4 Размытое Гауссом при S=6 – а и восстановленное изображения – б,
количество уровней дискретизации 64.

 

 

Рис.5 Размытое Гауссом при S=6 – а и восстановленное изображения – б,
количество уровней дискретизации 32

 

 

                  

Рис.6 Размытое Гауссом при S=6 – а и восстановленное изображения – б,
количество уровней дискретизации 16.

 

Рис.7 Размытое Гауссом при S=6 – а и восстановленное изображения – б,
количество уровней дискретизации 8.

 

Рис.8 Размытое Гауссом при S=6 – а и восстановленное изображения – б,
количество уровней дискретизации 4.

 

Из сравнения Рис.2-8 видно, что уменьшение количества уровней дискретизации заметно ограничивает возможности восстановления. При этом на первый взгляд исходные размытые изображения на Рис.2-5 не отличаются друг от друга.

Интересно, что, метод инверсной фильтрации для восстановления изображений с учетом квантования яркости при записи в BMP файл [1], улучшает изображения даже при малых уровнях дискретизации. Из иллюстраций видно, что часть деталей, не видимых из-за дискретизации проявилась на восстановленных изображениях.

Если увеличивать количество уровней дискретизации в восстанавливаемом (размытом) изображении (рис. 1), что соответствует получению изображения системами радиовидения большой точности (много большей чем 256 уровней дискретизации), то, используя метод [1] получим существенное улучшение восстанавливаемого изображения.

 

 

 

Рис.9 Восстановленные изображения соответственно при различном количестве уровней дискретизации яркости:
а)  65536;  б)  1.678∙10⁷;   в)  4.295∙10⁹;   г)  исходное размытое изображение при S=6.

 

На восстановленных изображениях хорошо видны артефакты в виде не ярких ореолов и пятен. Это явление хорошо известно и связано с тем, что спектр изображения имеет явно выраженную область с ненулевыми спектральными амплитудами на фоне области с нулевыми амплитудами.

Попробуем заполнить область спектра с нулевыми амплитудами соответствующими им пространственными гармониками взятыми из спектра размытого изображения (предварительно отмасштабировав их). На Рис.10-11 показаны результаты этой операции.

 

                

а                                                       б

Рис.10 Восстановленное изображение по методу [1] -а  и восстановленное изображение с раннее убранным шумом, умноженным на 16 - б. Количество уровней дискретизации – 256.

 

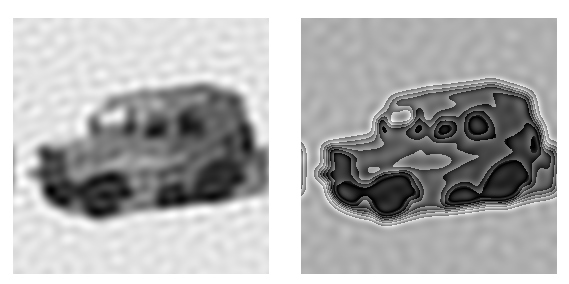
а                                                       б

Рис.11 Восстановленное изображение по методу [1] -а  и восстановленное изображение с раннее убранным шумом, умноженным на 4 - б. Количество уровней дискретизации – 8.

                                                                       

Из рисунка 10  можно увидеть, что, при таком подходе, частично артефакты подавляются, хотя и появляются новые. А Рис.11 показывает суть этой операции – добавление шумовой области спектра приводит к частичному восстановлению исходной дискретизации (как на размытом изображении). Таким образом, очевидно, что уменьшение количества уровней дискретизации N негативно сказывается на качестве восстановления, несмотря на то, что визуально исходные изображения с разными N не отличаются друг от друга. Априорное знание аппаратной функции и N позволяет при достаточно больших N существенно улучшить качество изображения.

 

Выводы.

Большой арсенал численных методов по восстановлению изображений [1, 2, 3, 4, 5, 6, 7] предусматривает борьбу шумами различных типов. Но при практической реализации любого из методов шум дискретизации может оказать определяющее влияние на конечный результат. 

В нашей работе, показано, что качество радиоизображения полученное с большим уровнем дискретизации (с большой точностью), при знании аппаратной функции системы радиовидения, может быть существенно улучшено численными методами. При проектировании систем радиовидения различного назначения, для оптимизации затрат, необходимо определить точность измерений и оценить то, на сколько можно улучшить результат с помощью дополнительной обработки полученных изображений.

 

Литература

1.  Зражевский А. Ю., Кокошкин А. В., Коротков В. А. «Особенности применения инверсной фильтрации для восстановления изображений с учетом квантования яркости при записи в BMP файл».  “ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ”  N 6, 2013  http://jre.cplire.ru/jre/jun13/14/text.html

2.  Р. Гонсалес,  Р. Вудс. Цифровая обработка изображений. М. «Техносфера» , 2005, 1071 стр.

3.  Тихонов А.Н., Арсенин В.Я. - Методы решения некорректных задач.       М.Наука, 1979

4.  Зражевский А.Ю., Кокошкин А.В., Новичихин Е.П., Титов С.В., «Повышение качества  радиоизображений». «Нелинейный Мир», № 9, 2010г., с. 582-590.

5.  Зражевский А. Ю., Кокошкин А. В. Влияние уровня боковых  лепестков   аппаратной функции на качество восстановленного изображения «Журнал Радиоэлектроники», №4, 2013г. http://jre.cplire.ru/jre/apr13/8/text.html

6.  Зражевский А. Ю., Коротков В. А. Исследование восстановления сигнала, прошедшего через неидеальный фильтр низких частот. «Журнал Радиоэлектроники», №4, 2013г. http://jre.cplire.ru/jre/apr13/4/text.html

7.  Зражевский А. Ю., Коротков В. А. Особенности восстановления искаженного оптической системой радиоизображения с помощью метода опорного изображения. «Журнал Радиоэлектроники», №4, 2013г. http://jre.cplire.ru/jre/apr13/3/text.html