| "ЖУРНАЛ РАДИОЭЛЕКТРОНИКИ" N 4 , 2000 |
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ИНДУЦИРОВАННОГО ИЗЛУЧЕНИЯ АНСАМБЛЯ ЖЕСТКИХ РОТАТОРОВ
Институт радиотехники и электроники РАН
Получена 18 апреля 2000 г.
На основании результатов, полученных методами вычислительного эксперимента, сделан вывод о возможности индуцированного излучения в классической активной среде, состоящей из жестких диполей-ротаторов. В приближении заданной амплитуды внешней волны определено максимальное значение к.п.д. взаимодействия ансамбля ротаторов с электромагнитным полем, которое составило величину ~54%.
Введение.
1. Физическая модель
рассматриваемой системы.
2. Численная модель системы.
3. Результаты численного
моделирования.
Выводы.
Приложение.
Модели классических активных сред, способных генерировать когерентные электромагнитные колебания, рассматриваются уже сравнительно давно [1,2]. К настоящему моменту достаточно полно изучены те из них, которые описывают электронные пучки как наиболее пригодные для многих технических приложений. Однако, после первых публикаций [3,4] сравнительно мало внимания было уделено другим типам классических активных сред, как искусственным [5], так и естественным. Например, в качестве активной среды может выступать ансамбль жестких ротаторов. Анализ возможности получения индуцированного излучения в такой системе впервые был проведен в [3]. В рамках линейного приближения было показано, что если внешнее электромагнитное излучение неполяризовано и имеет широкий угловой спектр, то ансамбль классических ротаторов ведет себя так же, как и ансамбль линейных осцилляторов, т.е. поглощает в среднем энергию электромагнитного поля. В то же время известно, что в ансамбле жестких ротаторов выполнены необходимые условия для вынужденного излучения в классической среде [1]: именно, в данном случае частота вращения ротатора прямо пропорциональна квадратному корню из кинетической энергии, а начальная скорость вращения обеспечивает "активность" среды
.Настоящая работа посвящена выяснению возможности индуцированного излучения в ансамбле классических двумерных жестких диполей-ротаторов для случая, когда внешнее поле представляет собой плоскую линейно поляризованную монохроматическую волну. Такая постановка задачи соответствует физической ситуации, имеющей место, например, при рассмотрении генераторов электромагнитных колебаний с высокодобротной электродинамической системой.
1. Физическая модель рассматриваемой системы.
Рассмотрим ансамбль ротаторов, вид которых представлен на рис.1. Ось вращения каждого ротатора перпендикулярна соединяющему сосредоточенные массы стержню и проходит через его середину. Все ротаторы расположены в одной плоскости, и оси их вращения параллельны.
Положим, что в начальный
момент времени ротаторы имеют одинаковую
кинетическую энергию и сонаправленные вектора
угловых скоростей, а начальная фаза вращения
равномерно распределена по ансамблю в интервале ![]()
Линейный размер системы
полагаем малым по сравнению с длиной волны,
соответствующей дипольному излучению на
начальной частоте вращения частиц ансамбля ![]() . В этом случае
пространственное распределение
электромагнитного поля внешней плоской волны,
частота
. В этом случае
пространственное распределение
электромагнитного поля внешней плоской волны,
частота ![]() которой
близка к
которой
близка к ![]() ,
внутри системы в каждый момент времени можно
считать однородным.
,
внутри системы в каждый момент времени можно
считать однородным.
Будем рассматривать динамику системы в предположении заданной амплитуды внешней волны и невзаимодействующих ротаторов.
Пренебрегая влиянием магнитного поля плоской волны, уравнения движения ротаторов запишем в следующем виде:
(1) 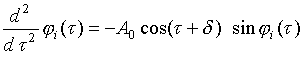
где ![]() - фаза вращения
- фаза вращения
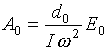 ,
,
![]() - амплитуда внешней волны,
- амплитуда внешней волны,
 - момент инерции ротатора,
- момент инерции ротатора,
![]() - модуль его дипольного
момента,
- модуль его дипольного
момента,
![]() - ее начальная фаза,
- ее начальная фаза,
![]() .
.
Полное решение системы (1) можно получить используя, например, численные методы.
Численное моделирование ансамбля ротаторов проводилось методом макрочастиц [6]. В начальный момент макрочастицы были равномерно распределены как по фазе вращения, так и по фазе внешней волны.
Для численного решения (1) использовался "метод с перешагиванием":
![]()
(2)
![]()
где ![]() - шаг интегрирования по времени,
- шаг интегрирования по времени, 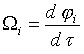
Сдвиг на половину временного шага значения частоты вращения относительно значения угла учитывался при формировании выходных интегральных характеристик динамики ансамбля (например, суммарной кинетической энергии).
Количество ![]() "макрочастиц" определялось из
условия минимизации начальных флуктуаций
распределения по фазам вращения и внешней волны.
Проведенные тестовые вычисления показали, что
достаточно хороший результат можно получить уже
при
"макрочастиц" определялось из
условия минимизации начальных флуктуаций
распределения по фазам вращения и внешней волны.
Проведенные тестовые вычисления показали, что
достаточно хороший результат можно получить уже
при
![]() .
.
3. Результаты численного моделирования.
Численная модель была реализована на языке программирования С. Расчеты проводились на персональном компьютере с процессором P-II 300 МГц. Время выполнения одного варианта в среднем составляло 10 сек, что позволило провести оптимизацию решения для к.п.д. системы по двум входящим в (1) параметрам: амплитуде внешней волны и относительной расстройке частоты.
На рис.2. показаны
зависимости суммарной кинетической энергии
макрочастиц от времени при малых положительной
(кривая 1) и отрицательной (кривая 2) рассройках![]() . При
. При ![]() кинетическая энергия
ансамбля уменьшается (первый экстремум
зависимости является минимумом). Ротаторы
ансамбля образуют достаточно плотный фазовый
сгусток (рис.3, кривая 1). Следовательно, в этом
случае имеет место усиление электромагнитного
поля частицами ансамбля.
кинетическая энергия
ансамбля уменьшается (первый экстремум
зависимости является минимумом). Ротаторы
ансамбля образуют достаточно плотный фазовый
сгусток (рис.3, кривая 1). Следовательно, в этом
случае имеет место усиление электромагнитного
поля частицами ансамбля.
Из вида распределения макрочастиц по фазе вращения в моменты времени, соответствующие первому (рис.3., кривая 1) и второму (рис.3., кривая 2)) минимуму суммарной кинетической энергии, можно сделать вывод о том, что ограничение роста к.п.д. вызвано разрушением фазового сгустка макрочастиц.
На рис.4. показана
зависимость к.п.д. энергообмена от ![]() при оптимальном значении
амплитуды внешнего поля для случая, когда
линейные размеры, масса и дипольный момент
жесткого ротатора близки к соответствующим
характеристикам молекулы воды. Как видно из
рисунка, максимальный к.п.д. составил ~15% при
при оптимальном значении
амплитуды внешнего поля для случая, когда
линейные размеры, масса и дипольный момент
жесткого ротатора близки к соответствующим
характеристикам молекулы воды. Как видно из
рисунка, максимальный к.п.д. составил ~15% при ![]()
Результаты оптимизации
показали, что максимальный к.п.д. системы может
достигать 54% (![]()
Основываясь на полученных результатах, можно сделать вывод о возможности индуцированного излучения в ансамбле классических ротаторов.
Эффект, по-видимому, можно наблюдать либо в разреженных газах, состоящих из полярных молекул, либо в специально созданных искусственных активных средах.
Работа выполнена в рамках МНТП России "Физика микроволн" (Проект 1.12).
Приведенный ниже Java Applet реализует описанную в статье численную модель. Задав интересующие параметры системы, Вы можете получить зависимость нормированной энергии ансамбля ротаторов от безразмерного времени.
Описание параметров:
- количество шагов интегрирования (целое число);
- величина одного шага по времени (число с плавающей точкой);
- амплитуда внешней электромагнитной волны (число с плавающей точкой);
- начальная фаза внешней волны (число с плавающей точкой);
- относительная расстройка по частоте (число с плавающей точкой).
Все параметры представляют собой безразмерные величины. Нормировка соответствует п.п.1-2 статьи. Длина оси абсцисс представляемого графика соответствует полному времени интегрирования. Максимальное значение, отображаемое по оси ординат соответствует удвоенной начальной кинетической энергии ансамбля. Для увеличения скорости счета, количество частиц фиксировано и равно 150.
1. Гапонов А.В. //ЖЭТФ, 1960, Т.39, №2, С.326.
2. Hirshfield J.L., Wachtel J.M. //Phys.Rev.Lett., 1959, v.12., p.533.
3. Собельман И.И., Тютин И.В. //УФН, 1963, Т.79, №4, С.595.
4. Гапонов А.В., Петелин М.И., Юлпатов В.К. //Изв. ВУЗов СССР, Радиофизика, 1967, Т.10, №9-10, С.1414.
5. Корженевский А.В., Корниенко В.Н., Черепенин В.А. //РЭ, 1998, том 43, №4, с.1-6.
6. Рошаль А.С. Моделирование заряженных пучков. -М.: Атомиздат, 1979.
Авторы: Корниенко Владимир Николаевич, e-mail: korn@mail.cplire.ru