Дисперсия диэлектрических коэффициентов и

ac-проводимости монокристаллов TlGa_1–хСо_хS₂  в радиочастотном диапазоне

  

С. Н. Мустафаева
Институт физики Национальной академии наук Азербайджана, Баку

 

Получена 27 марта 2009 г.

 

                        

В слоистых монокристаллах TlGa_1–хСо_хS₂ (х = 0.005; 0.01) изучены частотные зависимости диэлектрических характеристик и ac-проводимости (s_ac) поперек слоев в частотном диапазоне f = 5×10⁴¸3.4×10⁷ Гц. Установлено, что в TlGa_1–хСо_хS₂ наряду с потерями на электропроводность имеют место также релаксационные потери. Обнаружено, что в частотной области 5×10⁴¸2.10⁷ Гц в монокристаллах TlGa_1–хСо_хS₂ имеет место прыжковый механизм переноса заряда по локализованным вблизи уровня Ферми состояниям. Оценены плотность (N_F) и энергетический разброс (ΔE) этих состояний, среднее время (τ) и расстояние (R) прыжков. Изучено влияние состава кристаллов TlGa_1–хСо_хS₂ на их диэлектрические коэффициенты. Установлено, что с ростом содержания кобальта в кристаллах N_F и ΔE возрастают, а τ  и R уменьшаются.
 

Ключевые слова: электродинамика конденсированных сред, слоистые монокристаллы.

 

ВВЕДЕНИЕ

 

    Слоистые монокристаллы TlGaS₂ характеризуются довольно высокой плотностью локализованных вблизи уровня Ферми состояний (N_F). Значения N_F, вычисленные на основе экспериментальных результатов измерения  dc и ac-проводимости монокристаллов TlGaS₂, составляли  ~ 2.0×10¹⁸эВ^–1см^–3 [1,2]. Легирование этих монокристаллов позволяет управлять их физическими свойствами. Так, например, в [3] было показано, что частичное замещение галлия в TlGaS₂ марганцем приводит к значительному уменьшению диэлектрической проницаемости, среднего времени и расстояния прыжков, а также увеличению плотности состояний на уровне Ферми.

Целью настоящей работы явилось изучение влияния частичного замещения галлия кобальтом в TlGaS₂ на диэлектрические свойства полученных кристаллов.

 

ЭКСПЕРИМЕНТАЛЬНАЯ ЧАСТЬ
 

 Характер взаимодействия в системе TlGaS₂ – TlCoS₂ был изучен [4] методами физико-химического анализа. Исходные соединения TlGaS₂ и TlCoS₂ были синтезированы в вакууме (10^–3 Па) в кварцевых ампулах прямым сплавлением высокочистых (≥ 99.999%) элементов (Tl, Ga, S, Co), взятых в стехиометрическом соотношении. Синтезированные образцы для гомогенизации были подвергнуты отжигу в вакууме при температуре 440 К в течение 20 суток. Установлено, что при комнатной температуре на основе   TlGaS₂ образуются твердые растворы TlGa_1–хСо_хS₂ вплоть до 15 мол.% TlCoS₂.  Методом Бриджмена были выращены образцы монокристаллов TlGa_1–хСо_хS₂ (х = 0.005 и 0.01). Указанные составы кристаллизовались в тетрагональной сингонии с параметрами кристаллической решетки а = 7.29; с = 29.90 Å.

Измерения диэлектрических свойств монокристаллов TlGa_1–хСо_хS₂ (х = 0.005 и 0.01) на переменном токе произведены резонансным методом с помощью куметра TESLA BM560. Диапазон частот переменного электрического поля составлял 5×10⁴ ¸ 3.4×10⁷  Гц.

Монокристаллические образцы из TlGa_1–хСо_хS₂ для электрических измерений были изготовлены в виде плоских конденсаторов, плоскость которых была перпендикулярна кристаллографической C-оси кристалла. В качестве электродного материала использована серебряная паста. Толщина образцов из TlGa_1–хСо_хS₂ составляла 100 – 140 мкм, а площадь обкладок –7.6·10^–2 cм². Все диэлектрические измерения монокристаллических образцов были проведены при 300 К. Воспроизводимость положения резонанса составляла по емкости   ± 0.2 пкФ, а по добротности (Q = 1/tgd)   ± 1.0 ¸1.5 деления шкалы. При этом наибольшие отклонения от средних значений составляли 3 – 4% для ε и 7% для tgd.

 

РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ
 

На рис. 1 приведены результаты измерения тангенса угла диэлектрических потерь tgd при частотах 5×10⁴ ¸ 3.4×10⁷  Гц в монокристаллах TlGa_1–хСо_хS₂ (х = 0; 0.005 и 0.01).

 

 

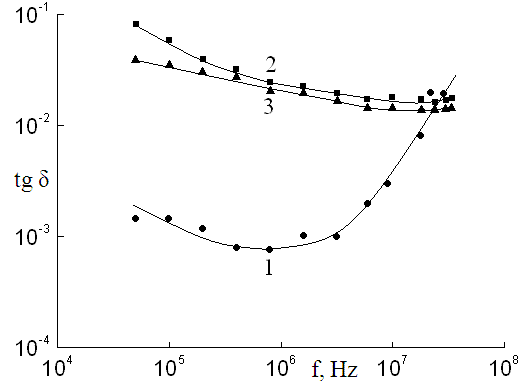
Рис. 1. Частотные зависимости тангенса угла диэлектрических потерь для монокристаллов TlGaS₂ (1); TlGa_0.995Со_0.005S₂ (2)  и TlGa_0.99Со_0.01S₂ (3) при Т = 300 К.

 

Из рис. 1 видно, что все приведенные   частотные зависимости tgd имеют монотонно спадающую ветвь. Уменьшение tgd с частотой по гиперболическому закону свидетельствует о том, что при этих частотах основным видом диэлектрических потерь в монокристаллах TlGa_1–хСо_хS₂ являются потери на электропроводность. В кристалле TlGaS₂ при f >10⁶  Гц наблюдалось существенное возрастание tgd с увеличением частоты вплоть до 3·10⁷ Гц.  Наличие возрастающей ветви на зависимости tgd (f) позволяет сделать вывод о том, что наряду с потерями на электропроводность вносят свой вклад и релаксационные потери. В отличие от монокристалла TlGaS₂ в образцах TlGa_1–хСо_хS₂ (х = 0.005; 0.01) после спада tgd наблюдалось незначительное его возрастание при f > 2·10⁷ Гц. Как видно из рис. 1 частота, при которой начинают проявляться релаксационные потери, смещается в сторону более высоких частот при частичном замещении галлия в TlGaS₂ кобальтом.

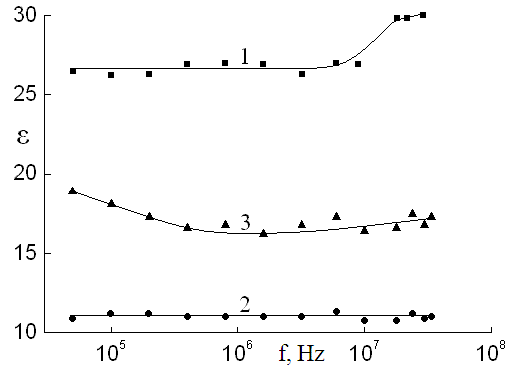
В области частот 5×10⁴ ¸ 3.4×10⁷  Гц измерена также электрическая емкость образцов TlGa_1–хСо_хS₂.  По значениям  емкости (С)  образцов при различных частотах рассчитаны значения диэлектрической проницаемости (e = C·L/ε₀S; L – толщина кристалла;  S – площадь обкладок конденсатора; ε₀ – диэлектрическая постоянная). На рис. 2 представлены частотные зависимости e для образцов TlGa_1–хСо_хS₂ различного состава (кривые 1 – 3).  Видно, что при введении кобальта в кристаллы TlGaS₂ диэлектрическая проницаемость значительно уменьшается при всех указанных частотах. Из рис. 2 видно, что в образцах TlGaS₂ и TlGa_0.995Со_0.005S₂ не наблюдается ощутимое изменение e с изменением частоты. А в образце TlGa_0.99Со_0.01S₂ диэлектрическая проницаемость монотонно уменьшалась с ростом частоты, что свидетельствует о релаксационной дисперсии.

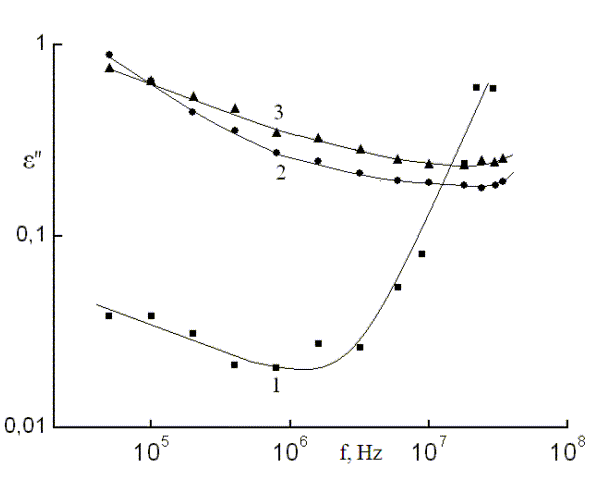
На рис. 3 приведены дисперсионные кривые коэффициента диэлектрических потерь (e″ = e·tgd) в монокристаллах TlGa_1–хСо_хS₂ различного состава. Видно, что при введении кобальта в кристаллы TlGaS₂ характер дисперсионных кривых e″(f) существенно изменяется. Если для TlGaS₂ кривая e″(f) имеет две ветви: слабо спадающую и резко возрастающую при f >10⁶ Гц, то в случае TlGa_1–хСо_хS₂ кривые e″(f) характеризуются довольно ощутимым спадом вплоть до 2·10⁷ Гц, после чего значения e″ проявляют тенденцию к увеличению.

 

Рис. 2. Частотная дисперсия диэлектрической проницаемости для монокристаллов TlGaS₂ (1); TlGa_0.995Со_0.005S₂ (2)  и TlGa_0.99Со_0.01S₂ (3).

 

Нами изучены также  частотные зависимости ac-проводимости монокристаллов TlGa_1–хСо_хS₂ при Т = 300 К (рис. 4). В области частот  f = 5×10⁴¸10⁶ Гц ac-проводимость монокристалла TlGaS₂ (кривая 1) изменялась по закону  s_ac~ f ^0.8, а при   f = 10⁶ ¸ 3×10⁷  Гц – по квадратичному закону s_ac~ f ². В [5] показано, что проводимость, пропорциональная  f ², обусловлена оптическими переходами в полупроводниках и вносит преобладающий вклад при высоких частотах. Дисперсионные кривые s_ac(f) образцов TlGa_1–хСо_хS₂ (рис. 4, кривые 2 и 3) характеризуются зависимостью s_ac~ f ^0.8 в более широкой области частот Δf: при х = 0.005  Δf = (5·10⁴ ¸10⁷) Гц, а при х = 0.01  значение Δf = (5·10⁴ ¸2·10⁷) Гц, т.е. увеличение содержания кобальта в кристаллах приводит к удлинению участка f ^0.8. При дальнейшем увеличении частоты зависимость s_ac от f становилась суперлинейной.

Рис. 3. Дисперсионные кривые коэффициента диэлектрических потерь в монокристаллах TlGaS₂ (1); TlGa_0.995Со_0.005S₂ (2)  и TlGa_0.99Со_0.01S₂ (3).

 

Наблюдение участка s_ac~ f ^0.8 на кривых s_ac(f)  свидетельствует о том, что в указанном диапазоне частот проводимость монокристаллов TlGa_1–хСо_хS₂ обусловлена прыжками носителей  заряда между локализованными вблизи уровня Ферми состояниями. В [6] для такого механизма переноса заряда было получено следующее выражение:
 

                                  s_ac(f) = (p³ / 96)× е² к Т N²_F a⁵ f [ln (n_ph / f)]⁴,                                        (1)
 

где е – заряд электрона, к – постоянная Больцмана,  N_F – плотность локализованных состояний вблизи уровня Ферми, а = 1/a – радиус локализации, a – постоянная спада волновой функции локализованного носителя заряда Y~е^–ar,  n_ph – фононная частота.
 

Рис. 4. Частотные зависимости ас-проводимости монокристаллов TlGaS₂ (1); TlGa_0.995Со_0.005S₂ (2)  и TlGa_0.99Со_0.01S₂ (3).

 

 

По экспериментально найденным значениям s_ac(f) и с помощью формулы (1) вычислили плотность состояний на уровне Ферми. Для монокристаллических образцов TlGa_1–хСо_хS₂ (х = 0.005; 0.01) значения N_F составляли соответственно 7.9×10¹⁸  и 9.1×10¹⁸  эВ^–1×cм^–3. Для образца TlGaS₂ N_F = 2.1×10¹⁸  эВ^–1×cм^–3 [2].    При вычислении N_F для радиуса локализации образцов TlGa_1–хСо_хS₂ брали значение а = 14 Å по аналогии с моносульфидом галлия [7], являющимся бинарным аналогом TlGaS₂. Значение n_ph для TlGaS₂ – порядка 10¹² Гц [8].

Теория прыжковой проводимости на переменном токе позволяет по формуле [5]:
 

R = (1/2a) ln (n_ph / f)                                              (2)
 

определить среднее расстояние прыжков. В формуле (2) 1/f = τ – среднее время прыжков.  Значение τ^–1 находится как средняя частота, при которой для s_ac наблюдается  f ^0.8 – закон. В монокристаллах TlGa_1–хСо_хS₂ значения τ составляли 0.2 мкс для х = 0.005 и 0.1 мкс для х = 0.01. Среднее время прыжков в монокристаллических образцах TlGa_1–хСо_хS₂ было значительно меньше, чем в TlGaS₂ (в TlGaS₂ τ = 2.0 мкс [2]). Вычисленные по формуле (2)  значения  R для монокристаллов TlGa_1–хСо_хS₂  с составами х = 0.005 и 0.01 составили 86 и 81Å, соответственно. Для монокристалла TlGaS₂ R = 103Å [2]. Значения  R примерно в 6 раз превышают среднее расстояние между центрами локализации носителей заряда в изученных монокристаллах (в TlGaS₂ R/a = 7.3 [2]).

По формуле  [5]:

   ΔЕ = 3/(2 πR³N_F)                                                           (3)
 

оценили энергетический разброс локализованных в окрестности уровня Ферми состояний. Значения ΔЕ, полученные для TlGa_1–хСо_хS₂, составили 9×10^–2 эВ при х = 0.005 и 9.7×10^–2 эВ при х = 0.01. Концентрация глубоких ловушек, ответственных за ac-проводимость, определенная по формуле:  N_t = N_F×ΔЕ, составляла 7.1×10¹⁷ cм^–3 в TlGa_0.995Со_0.005S₂ и 8.8×10¹⁷ cм^–3 в TlGa_0.99Со_0.01S₂.

На рис. 5 представлены для сравнения зависимости N_F, τ и R   от состава монокристаллов  TlGa_1–хСо_хS₂. Из этих зависимостей видно, что с ростом содержания кобальта в кристаллах плотность состояний, локализованных вблизи уровня Ферми, возрастает, а среднее время и расстояние прыжков уменьшаются.

Рис. 5. Зависимость параметров N_F, τ и R от состава монокристаллов TlGa_1–хСо_хS₂.

 

ЗАКЛЮЧЕНИЕ
 

Таким образом, изучена частотная дисперсия диэлектрических свойств монокристаллов TlGa_1–хСо_хS₂ различного состава.  Установлена природа диэлектрических потерь, механизм переноса заряда и оценены: плотность состояний вблизи уровня Ферми, их энергетический разброс, среднее время и расстояние прыжков, а также концентрация глубоких ловушек, ответственных за ac-проводимость. Обнаружено, что частичное замещение галлия кобальтом в монокристаллах TlGaS₂ позволяет управлять диэлектрическими характеристиками полученных кристаллов.

 

СПИСОК ЛИТЕРАТУРЫ

1. Мустафаева С.Н., Алиев В.А., Асадов М.М. Прыжковая проводимость на постоянном токе в монокристаллах  TlGaS₂ и TlInS₂ // ФТТ. 1998. Т. 40. № 4. С. 612 – 615.

2. Мустафаева С.Н. Частотная дисперсия диэлектрических коэффициентов слоистых монокристаллов TlGaS₂ // ФТТ. 2004. Т. 46. №  6. C. 979 – 981.

3. Мустафаева С.Н. Диэлектрические свойства монокристаллов   TlGa_1–xMn_xS₂ (0 £ x < 0.03) // Изв. РАН. Неорганические материалы. 2006. Т. 42.  № 5. С. 530 – 533.

4. Mustafaeva S.N., KerimovaE.M., Seidov F.M., Jabbarly A.I. Novel Thermoelectric Materials on the Base of TlGaS₂ – TlCoS₂ // Book of Abstracts of 13-th International Conference on Ternary and Multinary Compounds (ICTMC 13). Paris. France. October 14 – 18. 2002. P. 125.

5.  Мотт Н., Девис Э. Электронные процессы в некристаллических веществах. М.:   Мир. 1974. 472 с.

6.  Pollak M. Frequency dependence of conductivity in amorphous solids // Philos. Mag. 1971. V. 23. P. 519 – 542.

7.  Augelli V., Manfredotti C., Murri R. et al. Anomalous impurity conductivity in n-GaSe and n-GaS // L. Nuovo Cimento. B. 1977. V. 38. No 2. P. 327 – 336.

8. Аллахвердиев К.Р., Виноградов Е.А., Нани Р.Х. и др. Колебательный спектр кристаллов TlGaS₂, TlGaSe₂ и β-TlInS₂ // Физические свойства сложных полупроводников. Баку: Элм. 1982. С. 55 – 63.