УДК 621.396.67
АНТЕННА – ФИЛЬТР
С.Е.
Банков 1, А.Г. Давыдов 2, А.А. Курушин 3
1ИРЭ им. В.А. Котельникова РАН, 2МКБ Компас, 3МЭИ
(ТУ)
Получена 20 апреля 2010 г.
Аннотация. Рассмотрены вопросы моделирования, проектирования и экспериментального исследования печатных антенн СВЧ диапазона, которые содержат резонансный излучатель и неизлучающий резонатор. Показано, что такие антенны могут выполнять функцию двухзвенного полосового фильтра. Анализируются особенности синтеза обобщенных параметров таких фильтров. Предложен ряд моделей антенн – фильтров: феноменологическая модель в виде системы обобщенный связанных резонаторов, феноменологическая модель в виде системы связанных резонаторов на основе отрезков линий передачи, электродинамические модели. Представлены результаты экспериментального исследования антенн – фильтров.
Ключевые слова: антенна, печатная антенна, антенна – фильтр.
1. Постановка задачи
Печатные антенны (ПА) находят широкое применение во многих радиоэлектронных системах. К показателям качества (ПК) ПА часто предъявляются противоречивые требования, например уменьшения габаритов и расширения полосы рабочих частот. Следует также отметить, что при использовании ПА в составе приемной аппаратуры типичной является ситуация, когда последовательно с антенной включен полосовой фильтр, выполняющий функцию предварительной частотной селекции сигналов. В качестве примера такого использования ПА можно отметить приемную аппаратуру систем спутниковой навигации GPS и ГЛОНАС.
Уменьшение габаритов ПА влечет за собой увеличение ее добротности. Поэтому миниатюрную ПА можно рассматривать как резонатор, способный выполнять функцию частотной селекции. Это позволяет видоизменить структуру входной части приемного устройства за счет объединения двух функций: приема/передачи сигналов и их частотной селекции. Для этого ПА должна быть связана с дополнительными резонаторами, которые вместе с ПА образуют фильтр с частотной характеристикой того или иного вида, например чебышевского типа. Такую структуру можно назвать антенной – фильтром (АФ). Объединение двух функций в одном устройстве может существенно улучшить ПК аппаратуры в целом за счет сокращения ее габаритов и уменьшения стоимости.
Особенностью АФ является то, что в отличие от обычного фильтра роль одного из ее выходов играет свободное пространство. Это существенно изменяет как систему параметров, описывающих данное устройство, так и методы его проектирования. Целью нашей работы является разработка таких методов и их апробация на ряде конкретных примеров. В качестве ПА мы взяли широко распространенную ПА прямоугольной формы. В рамках данной работы мы ограничились исследованием АФ, содержащих один дополнительный резонатор и имеющих по этой причине характеристику второго порядка.
В предлагаемой работе будут рассмотрены следующие вопросы:
- конструкции АФ с линейной и круговой поляризациями и принципы их функционирования;
- оценка потерь в полосе пропускания АФ;
- феноменологическая модель АФ в виде системы связанных резонаторов на основе отрезков линий передачи;
- электродинамическая модель АФ, построенная с помощью современных систем численного моделирования;
- экспериментальная настройка и исследование АФ с линейной поляризацией.
2. Конструкции и внешние параметры АФ
а б
в г
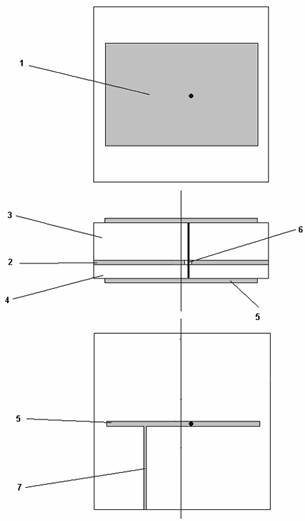
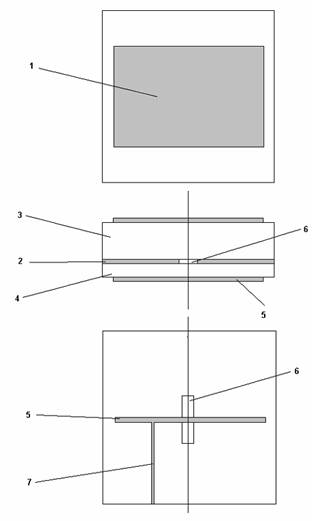
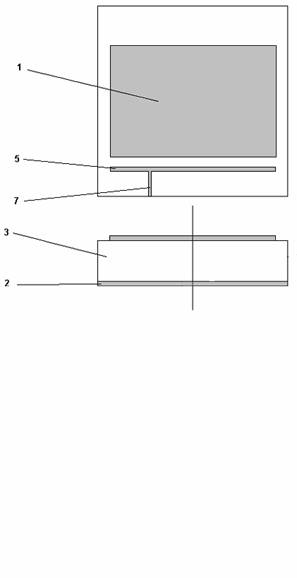
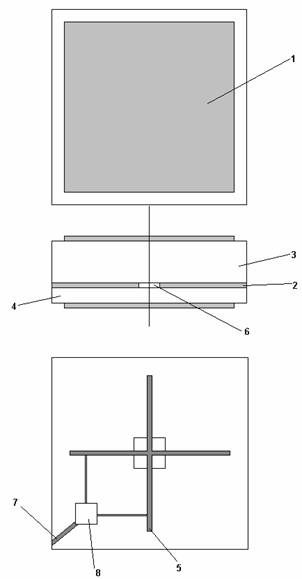
Рис. 1. Варианты антенн-фильтров.
На рис. 1 а-г показаны возможные варианты выполнения АФ. Позиции 1-9 обозначают разные элементы конструкции антенны:
1 – полосковый проводник ПА прямоугольной формы;
2 – экран ПА, который является общим экраном для ПА и резонатора;
3 – диэлектрическая подложка ПА;
4 – диэлектрическая подложка резонатора, который выполнен в виде отрезка микрополосковой линии (МПЛ);
5 – полосковый проводник резонатора;
6 – элемент связи ПА и резонатора, который выполнен в виде металлического цилиндра (рис. 1 а) или щели в общем экране (рис. 1 б,г);
7 – выходная МПЛ;
8 – квадратурный делитель мощности.
Антенны, изображенные на рис. 1 а-в, относятся к антеннам линейной поляризации, а на рис. 1 г к антеннам круговой поляризации излучаемых (принимаемых) волн. Общими элементами всех представленных АФ являются ПА и резонатор в виде отрезка МПЛ (МПЛ резонатор). В антеннах с линейной поляризацией поля ПА имеет прямоугольную форму, что обеспечивает разнос резонансных частот ортогональных собственных колебаний ПА. Наоборот, ПА, функционирующая на волнах с круговой поляризацией, имеет квадратную форму и одинаковые частоты ортогональных колебаний. По этой же причине остальные элементы АФ имеют симметрию поворота на 90 градусов: щель связи выполняется квадратной формы, а МПЛ резонатор представляет собой два скрещенных отрезка МПЛ. Симметрия этого типа обеспечивает возможность одновременного возбуждения ортогональных колебаний. В идеальном случае амплитуды колебаний должны быть одинаковыми по модулю и сдвинуты по фазе на 90 градусов. Такое соотношение между амплитудами колебаний обеспечивается квадратурным делителем мощности 8.
Отметим, что антенны, работающие на волнах с круговой поляризацией, могут быть рассмотрены как две независимые антенны линейной поляризации. Поэтому для простоты изложения принципов функционирования АФ мы ограничимся антеннами линейной поляризации. Принцип функционирования поясняет структурная схема АФ, показанная на рис. 2.
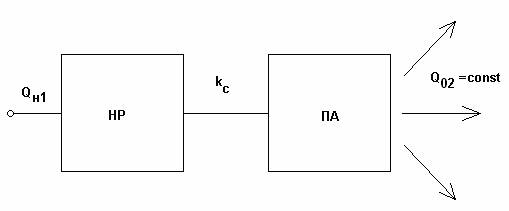
Рис. 2. Структурная схема антенны-фильтра.
Изображенная на рис. 2 схема
АФ состоит из ПА и резонатора, который обозначен как неизлучающий резонатор
(НР). Этот термин подчеркивает важное требование, которое предъявляется к
дополнительному резонатору, входящего в состав АФ – малый уровень его потерь на
излучение. Потери в резонаторе принято описывать с помощью параметра
добротности. Потерям разной природы сопоставим разные виды добротностей: потери
на излучение – радиационную добротность ![]() , тепловые потери – добротность
, тепловые потери – добротность ![]() , потери на связь с
внешней схемой – добротность связи
, потери на связь с
внешней схемой – добротность связи ![]() . Если принять, что индекс 1 соответствует
НР, а индекс 2 ПА, то математически требование малых потерь на излучение у НР
можно выразить следующим неравенством:
. Если принять, что индекс 1 соответствует
НР, а индекс 2 ПА, то математически требование малых потерь на излучение у НР
можно выразить следующим неравенством:
![]() . (1)
. (1)
Смысл условия (1) состоит в том, что излучение из АФ должно формироваться только ПА. Необходимость его выполнения можно пояснить следующим образом. В системе связанных резонаторов возбуждаются собственные колебания, поле которых существует во всех резонаторах одновременно. Эти колебания имеют разные резонансные частоты, что в конечном итоге обеспечивает формирование частотной характеристики фильтра. Структуры полей у разных собственных колебаний могут существенно отличаться. Поэтому, если все резонаторы будут излучать в свободное пространство, то характеристики излучения, например диаграммы направленности, разных собственных колебаний будут существенно разными из-за интерференции полей. В этом случае весьма сложно добиться одинаковой интенсивности излучения в полосе пропускания фильтра.
Если условие (1) выполняется, то все колебания излучают в свободное пространство с одинаковой диаграммой направленности (ДН), которая совпадает с ДН ПА. Идентичность характеристик излучения разных собственных колебаний резонансной системы является фактором, который существенно облегчает формирование частотной характеристики АФ заданной формы.
Отличие структурной схемы АФ
показанной на рис. 2, от традиционного полосового фильтра состоит в том, что ПА
в качестве одного из своих входов имеет свободное пространство. Распределение
излучения ПА в свободном пространстве описывается с помощью ДН, которая
является функцией двух угловых координат ![]() (сферическую систему координат введем, как
показано на рис. 3).
(сферическую систему координат введем, как
показано на рис. 3).
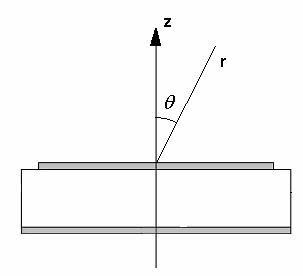
Рис. 3. К определению сферической системы координат.
Для описания энергетических характеристик антенны традиционно используют такой параметр, как коэффициент усиления (КУ), который определяется следующим образом:
 , (2)
, (2)
где ![]() - мощность, подведенная к входу ПА,
- мощность, подведенная к входу ПА, ![]() - вектор Пойнтинга в
направлении, задаваемом углами
- вектор Пойнтинга в
направлении, задаваемом углами ![]() на сфере радиуса
на сфере радиуса ![]() , который, вообще говоря, должен
стремиться к бесконечности. Чаще всего при определении КУ используется
направление максимального излучения. В случае ПА оно обычно характеризуется
углом
, который, вообще говоря, должен
стремиться к бесконечности. Чаще всего при определении КУ используется
направление максимального излучения. В случае ПА оно обычно характеризуется
углом ![]() (величина
(величина
![]() при этом
значения не имеет).
при этом
значения не имеет).
Полная мощность излучения
антенны ![]() определяется
следующим образом:
определяется
следующим образом:
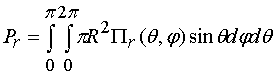 . (3)
. (3)
Предположим, что полная
мощность излучения меняется при изменении частоты пропорционально амплитуде
вектора Пойнтинга в заданном направлении ![]() . Это предположение связано с тем, что
благодаря резонансным свойствам ПА распределение ее излучающих токов слабо
зависит от частоты, по крайней мере, в пределах полосы пропускания АФ. При этом
амплитуда распределения тока может меняться весьма сильно.
. Это предположение связано с тем, что
благодаря резонансным свойствам ПА распределение ее излучающих токов слабо
зависит от частоты, по крайней мере, в пределах полосы пропускания АФ. При этом
амплитуда распределения тока может меняться весьма сильно.
В рамках принятого допущения
мы можем описывать частотные свойства ПА не с помощью КУ (2), а используя
коэффициент передачи ПА по мощности ![]() :
:
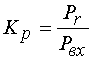 . (4)
. (4)
Коэффициент передачи ПА
по амплитуде ![]() определяется
как квадратный корень из
определяется
как квадратный корень из ![]() . Параметр
. Параметр ![]() более удобен для целей нашего
исследования, чем КУ. При этом его применение не вступает в противоречие с
использованием КУ, так как они имеют с точностью до постоянных множителей
одинаковые зависимости от частоты.
более удобен для целей нашего
исследования, чем КУ. При этом его применение не вступает в противоречие с
использованием КУ, так как они имеют с точностью до постоянных множителей
одинаковые зависимости от частоты.
По аналогии с
коэффициентом передачи ПА можно ввести коэффициенты передачи по мощности и
амплитуде всей АФ ![]() и
и
![]() :
:
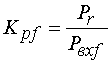 , (5)
, (5)
![]() ,
,
где ![]() - мощность на входе АФ. Будем понимать
далее под частотной характеристикой АФ зависимость коэффициента
- мощность на входе АФ. Будем понимать
далее под частотной характеристикой АФ зависимость коэффициента ![]() от частоты. Одной из
задач нашего исследования является выбор параметров АФ, обеспечивающих соответствие
функции
от частоты. Одной из
задач нашего исследования является выбор параметров АФ, обеспечивающих соответствие
функции ![]() известной
из теории фильтров [1] характеристике Чебышева.
известной
из теории фильтров [1] характеристике Чебышева.
3. Оценка потерь в полосе пропускания АФ
В данном разделе оценим потенциально достижимое значение потерь в полосе пропускания АФ, которое обусловлено наличием тепловых потерь в НР и ПА. Эту оценку проведем с помощью известного приближенного соотношения [1], которое получено для полосового фильтра, выполненного на одинаковых резонаторах:
где ![]() - ширина полосы пропускания,
- ширина полосы пропускания, ![]() - центральная частота
полосы пропускания, N
– число резонаторов (в рассматриваемом случае N=2),
- центральная частота
полосы пропускания, N
– число резонаторов (в рассматриваемом случае N=2), ![]() - собственная добротность резонаторов
фильтра,
- собственная добротность резонаторов
фильтра, ![]() -
потери в полосе пропускания, выраженные в децибелах. В формулу (6) входит
собственная добротность резонатора
-
потери в полосе пропускания, выраженные в децибелах. В формулу (6) входит
собственная добротность резонатора ![]() . Поэтому для корректного применения (6)
необходимо знать этот параметр.
. Поэтому для корректного применения (6)
необходимо знать этот параметр.
Задача определения
собственной добротности для НР и для ПА ставится по-разному. В случае НР
постановка задачи традиционна, так как НР имеет выход в виде линии передачи, к
которому можно подключить измерительную аппаратуру и измерить внешние
характеристики устройства. В качестве такой характеристики выступает частотная зависимость
коэффициента отражения ![]() . По этой характеристике можно определить,
в частности собственную добротность
. По этой характеристике можно определить,
в частности собственную добротность ![]() .
.
Добротность резонатора
можно определить по ширине резонансной кривой. При этом необходимо иметь в
виду, что этот параметр соответствует не собственной, а нагруженной добротности
![]() . Добротности
. Добротности ![]() и
и ![]() связаны известным соотношением:
связаны известным соотношением:
Формула (7) записана
применительно к НР. Об этом говорит индекс 1, входящий во все параметры из (7);
![]() - добротность связи.
- добротность связи.
Задача определения
добротностей разных видов по измеренным значениям коэффициента отражения решена
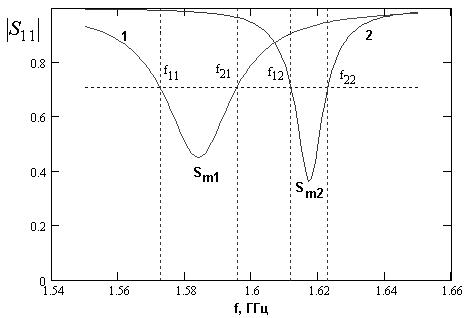
в работе [2]. Кратко остановимся на основных ее результатах. Частотная
зависимость модуля коэффициента отражения НР ![]() имеет характерный вид резонансного
провала, который показан на рис. 4. При этом различают три режима связи резонатора
с внешней схемой: докритический, критический и послекритический [2]. Эти три
режима поясняются на рис. 5, на котором показана зависимость модуля
коэффициента отражения
имеет характерный вид резонансного
провала, который показан на рис. 4. При этом различают три режима связи резонатора
с внешней схемой: докритический, критический и послекритический [2]. Эти три
режима поясняются на рис. 5, на котором показана зависимость модуля
коэффициента отражения ![]() на резонансной частоте от параметра
на резонансной частоте от параметра ![]() . Из рис. 5 видно, что
одному и тому же значению
. Из рис. 5 видно, что
одному и тому же значению ![]() соответствуют два значения
соответствуют два значения ![]() в докритическом и
послекритическом режимах. Однозначное соответствие
в докритическом и
послекритическом режимах. Однозначное соответствие ![]() и
и ![]() наблюдается только при критической связи,
когда
наблюдается только при критической связи,
когда ![]() . Однако
на практике точно настроиться на критическую связь весьма затруднительно.
Поэтому этот режим в случае высокоточных измерений лучше не рассматривать,
полагая, что связь резонатора с внешней схемой всегда либо докритическая, либо
послекритическая.
. Однако
на практике точно настроиться на критическую связь весьма затруднительно.
Поэтому этот режим в случае высокоточных измерений лучше не рассматривать,
полагая, что связь резонатора с внешней схемой всегда либо докритическая, либо
послекритическая.
Рис. 4. К определению добротности резонатора.
Идентификация режима, в котором находится резонатор, не
является сложной задачей. Для этого достаточно в резонатор ввести небольшие тепловые
потери. Если при этом параметр ![]() увеличивается, то режим докритический, а
если уменьшается, то послекритический.
увеличивается, то режим докритический, а
если уменьшается, то послекритический.

Рис. 5. К определению режима связи резонатора с внешней схемой.
Поскольку в соотношение (7) входят три неизвестные
величины, то для определения всех неизвестных параметров необходимо получить
еще два уравнения. Будем определять экспериментально (см. рис. 4) частоты ![]() , на которых
, на которых ![]() равен 0.707. Кроме
того, экспериментально определим величину
равен 0.707. Кроме
того, экспериментально определим величину ![]() . Тогда мы можем записать два следующих
уравнения:
. Тогда мы можем записать два следующих
уравнения:
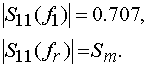 (8)
(8)
Совместное решение уравнений (8) приводит к следующему результату:
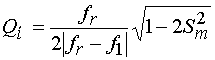 , (9)
, (9)
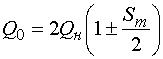 .
.
Знак плюс берется для послекритического режима, а минус - для докритического. Добротность связи легко определяется из формулы (7). Таким образом, первую задачу об экспериментальном определении добротностей НР можно считать решенной.
Решение аналогичной
задачи для ПА осложняется тем, что роль второго выхода фильтра, на который
нагружена ПА, играет свободное пространство. Поэтому добротность ![]() должна определяться со
стороны свободного пространства. В этом случае соотношение (7) для ПА принимает
следующий вид:
должна определяться со
стороны свободного пространства. В этом случае соотношение (7) для ПА принимает
следующий вид:
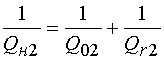 , (10)
, (10)
где ![]() - собственная добротность ПА,
обусловленная тепловыми потерями. Таким образом, в данном случае роль
добротности связи с внешней схемой играет радиационная добротность ПА
- собственная добротность ПА,
обусловленная тепловыми потерями. Таким образом, в данном случае роль
добротности связи с внешней схемой играет радиационная добротность ПА ![]() .
.
Будем измерять коэффициент отражения
от ПА со стороны ее входа, которым она в АФ соединена с НР. Проведем два
измерения собственной добротности. В первом случае испытывается излучающая ПА.
Это измерение дает величину ![]() , связанную с
, связанную с ![]() и
и ![]() соотношением, аналогичным (10):
соотношением, аналогичным (10):
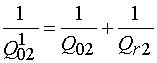 . (12)
. (12)
Во втором случае измеряется та же ПА, но закрытая
металлическим экраном. Экранировка ПА устраняет возможность излучения в
свободное пространство. Поэтому можно считать, что добротность ПА для этого случая
![]() равна
равна ![]() . Из результатов этих
двух опытов легко можно найти параметры
. Из результатов этих
двух опытов легко можно найти параметры ![]() и
и ![]() .
.
Кривые 1 и 2 на рисунке 4 получены экспериментально. Кривая 1 соответствует излучающей ПА, а кривая 2 - экранированной антенне. Существенно, что излучающая ПА находится в докритическом режиме, а экранированная ПА - в послекритическом.
Изложенная выше методика была применена для ПА со следующими
параметрами: размеры диэлектрической подложки 40х40х4 мм, диэлектрическая
проницаемость подложки 10 (материал ФЛАН-10), размеры металлизации 29.7х16 мм.
Были получены следующие результаты: ![]() =113,
=113, ![]() =300. Был также исследован НР в виде
отрезка МПЛ шириной 1 мм, выполненной на подложке из материала ФЛАН-10 толщиной
1 мм. Для него было получено значение собственной добротности
=300. Был также исследован НР в виде
отрезка МПЛ шириной 1 мм, выполненной на подложке из материала ФЛАН-10 толщиной
1 мм. Для него было получено значение собственной добротности ![]() =109.
=109.
Существенное различие собственных добротностей НР и ПА вполне естественно, так как объем, занятый НР, существенно меньше объема ПА.
Теперь можно воспользоваться
формулой (6). Для исследованных НР и ПА нетрудно получить, что ![]() = 1.7 дБ при
= 1.7 дБ при ![]() =1.6 ГГц и
=1.6 ГГц и ![]() =0.04 ГГц. В соотношении
(6) в качестве
=0.04 ГГц. В соотношении
(6) в качестве ![]() использовалось
среднее арифметическое значение между
использовалось
среднее арифметическое значение между ![]() и
и ![]() . Отметим, что соотношение (6) дает оценку
затухания в полосе пропускания, обусловленного только тепловыми потерями.
Полное затухание будет больше величины, определяемой (6), так как к тепловым
потерям добавятся потери, обусловленные рассогласованием устройства.
. Отметим, что соотношение (6) дает оценку
затухания в полосе пропускания, обусловленного только тепловыми потерями.
Полное затухание будет больше величины, определяемой (6), так как к тепловым
потерям добавятся потери, обусловленные рассогласованием устройства.
4. Модель АФ в системы резонаторов на основе отрезков линий передачи
Дальнейшее исследование АФ связано с расчетом ее частотных характеристик. Для этого необходимо построить математическую модель АФ. Наиболее полное решение этой задачи может быть получено на основе использования численных методов расчета трехмерных структур, основанных на строгой постановке электродинамической задачи (см. например работу [3]). Однако, это требует весьма больших компьютерных ресурсов, в первую очередь, времени, которое необходимо для получения численного результата. Поэтому для качественного понимания основных закономерностей функционирования АФ целесообразно использовать более простые модели, позволяющие за ограниченное время провести анализ большого числа вариантов. Такую модель можно получить, заменяя НР и ПА отрезками линий передачи.
Рассмотрим
такой подход применительно к АФ с зондовой связью, которая показана на
рис. 1
а. Модель АФ изображена на рис. 6. НР и ПА представлены в виде совокупности
отрезков линий передачи, которые имеют электрическую длину ![]() и характеристическое
сопротивление
и характеристическое
сопротивление ![]() .
Электрическая длина задается на частоте
.
Электрическая длина задается на частоте ![]() . Схема содержит два резонатора. На рис. 6
они расположены один под другим. Нижний резонатор соответствует НР, а верхний
ПА. Электрические длины резонаторов
. Схема содержит два резонатора. На рис. 6
они расположены один под другим. Нижний резонатор соответствует НР, а верхний
ПА. Электрические длины резонаторов ![]() близки к
близки к ![]() , что обеспечивает равенство их резонансных
частот
, что обеспечивает равенство их резонансных
частот ![]() частоте
частоте
![]() . Значение
. Значение ![]() отличается от
отличается от ![]() из-за реактивности,
вносимой индуктивностью связи
из-за реактивности,
вносимой индуктивностью связи ![]() . Поэтому для компенсации ее влияния
приходится немного увеличивать электрические длины резонаторов.
. Поэтому для компенсации ее влияния
приходится немного увеличивать электрические длины резонаторов.
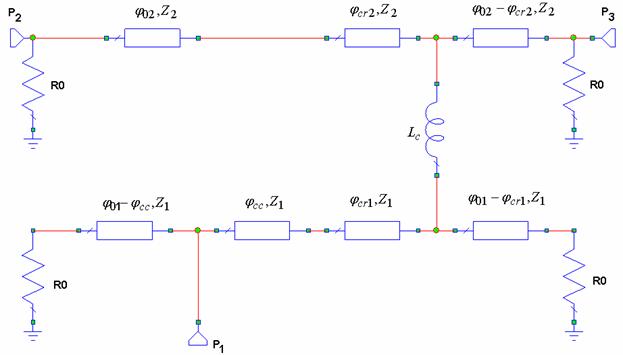
Рис. 6. Модель антенны-фильтра на основе связанных линий передачи.
Электрическая
длина ![]() описывает
смещение точки подключения выходной линии передачи относительно центра НР. Сама
выходная линия моделируется портом
описывает
смещение точки подключения выходной линии передачи относительно центра НР. Сама
выходная линия моделируется портом ![]() , который имеет сопротивление равное 50 Ом.
, который имеет сопротивление равное 50 Ом.
Резонаторы
нагружены на резисторы ![]() , которые учитывают тепловые потери.
Номиналы резисторов выбираются таким образом, чтобы собственные добротности
резонаторов модели и реальных ПА и НР совпадали. Верхний резонатор также имеет
на концах нагрузки в виде портов
, которые учитывают тепловые потери.
Номиналы резисторов выбираются таким образом, чтобы собственные добротности
резонаторов модели и реальных ПА и НР совпадали. Верхний резонатор также имеет
на концах нагрузки в виде портов ![]() . Эти нагрузки учитывают излучение из ПА.
Сопротивления портов выбираются из условия равенства суммарной добротности
верхнего резонатора добротности ПА, которая обусловлена тепловыми потерями и
потерями на излучение.
. Эти нагрузки учитывают излучение из ПА.
Сопротивления портов выбираются из условия равенства суммарной добротности
верхнего резонатора добротности ПА, которая обусловлена тепловыми потерями и
потерями на излучение.
Электрические
длины ![]() описывают
смещение точек включения элемента связи относительно центра НР и ПА
соответственно. Резонаторы, показанные на рис. 6, образованы линиями передачи с
разными характеристическими сопротивлениями
описывают
смещение точек включения элемента связи относительно центра НР и ПА
соответственно. Резонаторы, показанные на рис. 6, образованы линиями передачи с
разными характеристическими сопротивлениями ![]() . Сопротивление НР
. Сопротивление НР ![]() можно определить по
геометрическим размерам линии передачи с помощью известных программ – таких,
например, как система Microwave Office (MWO). ПА можно
рассматривать как отрезок МПЛ шириной
можно определить по
геометрическим размерам линии передачи с помощью известных программ – таких,
например, как система Microwave Office (MWO). ПА можно
рассматривать как отрезок МПЛ шириной ![]() и высотой
и высотой ![]() . Тогда параметр
. Тогда параметр ![]() находится из следующего
приближенного соотношения:
находится из следующего
приближенного соотношения:
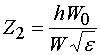 , (13)
, (13)
где
![]() -
волновое сопротивление свободного пространства,
-
волновое сопротивление свободного пространства, ![]() - относительная диэлектрическая
проницаемость материала, из которого выполнена ПА.
- относительная диэлектрическая
проницаемость материала, из которого выполнена ПА.
Не составляет труда
перейти от электрической длины отрезка линии передачи к его физической длине,
если известна постоянная распространения линии ![]() . Для НР она находится с помощью
упоминавшихся выше программ. В случае ПА она равна
. Для НР она находится с помощью
упоминавшихся выше программ. В случае ПА она равна ![]() , где
, где ![]() - волновое число свободного
пространства.
- волновое число свободного
пространства.
Индуктивность связи ![]() считаем заданным параметром, который
находится путем экспериментального измерения входного сопротивления ПА на
резонансной частоте. Его мнимая часть равна реактивному сопротивлению
индуктивности связи.
считаем заданным параметром, который
находится путем экспериментального измерения входного сопротивления ПА на
резонансной частоте. Его мнимая часть равна реактивному сопротивлению
индуктивности связи.
Таким образом, мы можем сделать вывод, что все параметры феноменологической модели, показанной на рис. 6, могут быть найдены экспериментальным или расчетным путем.
Рассмотрим
далее зависимость характеристик модели от ее параметров. Будем менять связь АФ
с внешней схемой, меняя положение точки подключения входной линии передачи. Она
задается электрической длиной ![]() . При этом связь резонаторов друг с другом,
которая задается параметром
. При этом связь резонаторов друг с другом,
которая задается параметром ![]() , остается постоянной. Из расчетных
частотных зависимостей коэффициента передачи АФ -
, остается постоянной. Из расчетных
частотных зависимостей коэффициента передачи АФ - ![]() находим такие характеристики АФ как полосу
пропускания
находим такие характеристики АФ как полосу
пропускания ![]() ,
потери в полосе пропускания
,
потери в полосе пропускания ![]() , неравномерность частотной характеристики
в полосе пропускания
, неравномерность частотной характеристики
в полосе пропускания ![]() ,
ширину полосы запирания
,
ширину полосы запирания ![]() .
.
Из
рис. 7-9, на которых показана частотная зависимость коэффициента передачи ![]() , можно видеть, каким
образом находятся указанные выше величины. Необходимо отметить, что при
увеличении связи с внешней схемой происходят качественные изменения частотной
характеристики
, можно видеть, каким
образом находятся указанные выше величины. Необходимо отметить, что при
увеличении связи с внешней схемой происходят качественные изменения частотной
характеристики ![]() .
Их можно увидеть, сравнивая рис. 7 и рис. 8. На рис. 7 кривая частотной
зависимости коэффициента передачи имеет двугорбый характер, соответствующий
чебышевской характеристике. При большей связи со схемой она становится
одногорбой. В двух разных случаях приходится по-разному определять полосу
пропускания АФ. Для двугорбой характеристики мы следовали стандартному
определению ширины полосы пропускания [1], принятому в теории фильтров. Для одногорбой
характеристики это понятие становится условным. Мы использовали определение,
связанное с уменьшением
.
Их можно увидеть, сравнивая рис. 7 и рис. 8. На рис. 7 кривая частотной
зависимости коэффициента передачи имеет двугорбый характер, соответствующий
чебышевской характеристике. При большей связи со схемой она становится
одногорбой. В двух разных случаях приходится по-разному определять полосу
пропускания АФ. Для двугорбой характеристики мы следовали стандартному
определению ширины полосы пропускания [1], принятому в теории фильтров. Для одногорбой
характеристики это понятие становится условным. Мы использовали определение,
связанное с уменьшением ![]() на 1 дБ относительно максимального
значения (см. рис. 8). При этом, как показала практика численных расчетов,
полосы пропускания, определенные разными способами, при изменении связи АФ с
внешней схемой переходят друг в друга без резких скачков.
на 1 дБ относительно максимального
значения (см. рис. 8). При этом, как показала практика численных расчетов,
полосы пропускания, определенные разными способами, при изменении связи АФ с
внешней схемой переходят друг в друга без резких скачков.
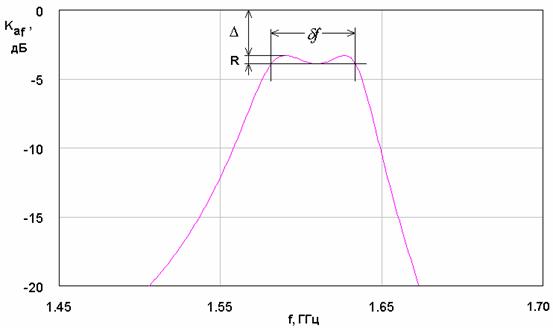
Рис. 7. Частотная характеристика антенны-фильтра при относительно слабой связи с внешней схемой.

Рис. 8. Частотная характеристика антенны-фильтра при относительно сильной связи с внешней схемой.
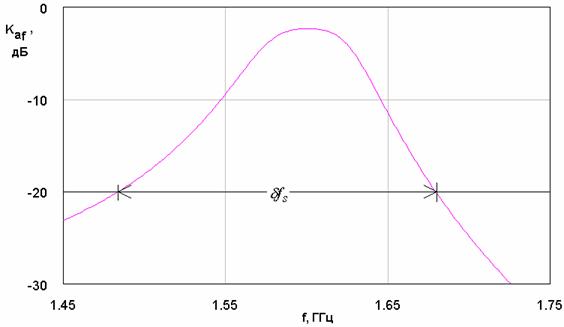
Рис. 9. К определению полосы запирания антенны-фильтра.
Полоса
запирания ![]() определялась
по уровню -20 дБ (см. рис. 9). Для описания частотной характеристики АФ за пределами
полосы пропускания мы использовали также такой параметр, как крутизна скатов
определялась
по уровню -20 дБ (см. рис. 9). Для описания частотной характеристики АФ за пределами
полосы пропускания мы использовали также такой параметр, как крутизна скатов ![]() . Он определялся
следующим образом:
. Он определялся
следующим образом:
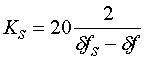 . (14)
. (14)
Крутизна скатов имеет размерность дБ/Гц и характеризует скорость изменения коэффициента передачи АФ в диапазоне между полосами пропускания и запирания.
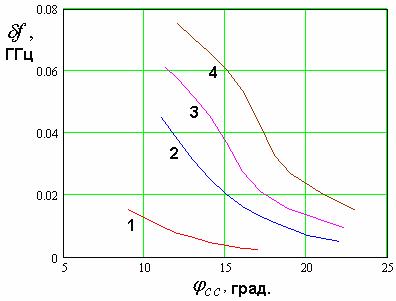
На рис. 10-14 показаны
зависимости указанных выше параметров АФ от величины ![]() . Кривые 1-4 на всех рисунках
соответствуют
. Кривые 1-4 на всех рисунках
соответствуют ![]() =20,25,27.5,30. Другие параметры
модели: Z1=25, Z2=50,
Q0=122, Qr=46. Оба резонатора имеют одинаковые собственные
добротности. Они обеспечиваются выбором резисторов
=20,25,27.5,30. Другие параметры
модели: Z1=25, Z2=50,
Q0=122, Qr=46. Оба резонатора имеют одинаковые собственные
добротности. Они обеспечиваются выбором резисторов ![]() =7950 Ом. Радиационная
добротность обеспечивается выбором импеданса портов 2 и 3, который равен 3000
Ом.
=7950 Ом. Радиационная
добротность обеспечивается выбором импеданса портов 2 и 3, который равен 3000
Ом.
Из рис. 10 видно, что при
увеличении связи АФ с внешней схемой ее полоса пропускания уменьшается. При
этом чем больше связь между резонаторами, тем больше абсолютное значение полосы
пропускания. Одновременно с этим происходит уменьшение неравномерности
частотной характеристики (см. рис. 11). Начиная с некоторого значения ![]() , параметр
, параметр ![]() становится равным нулю,
причем, чем меньше значение
становится равным нулю,
причем, чем меньше значение ![]() , тем раньше наступает переход од
двугорбой характеристики к одногорбой. Этому переходу соответствует условие
, тем раньше наступает переход од
двугорбой характеристики к одногорбой. Этому переходу соответствует условие ![]() =0.
=0.
Рис. 10. Зависимость полосы пропускания от связи с внешней схемой.
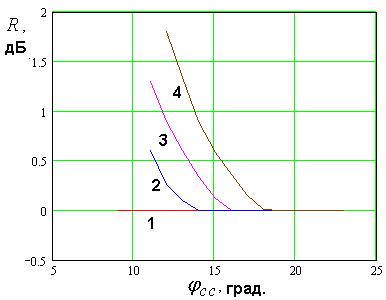
Рис. 11. Зависимость амплитуды пульсаций частотной характеристики антенны-фильтра от уровня связи с внешней схемой.
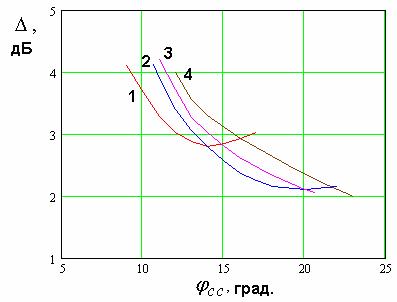
Рис. 12. Зависимость потерь антенны-фильтра в полосе пропускания от уровня связи с внешней схемой.
Зависимость потерь в полосе
пропускания ![]() от
от
![]() имеет минимум
(см. рис. 12). Значение
имеет минимум
(см. рис. 12). Значение ![]() , соответствующее минимуму потерь
увеличивается при увеличение
, соответствующее минимуму потерь
увеличивается при увеличение ![]() . С ростом этого параметра также
происходит уменьшение минимальных потерь АФ. Однако при этом следует иметь
ввиду, что своего минимума потери достигают, когда характеристика коэффициента
передачи становится одногорбой, то есть далекой от прямоугольной. Таким
образом, мы имеем противоречие между требованиями минимизации потерь и
прямоугольностью частотной характеристики АФ.
. С ростом этого параметра также
происходит уменьшение минимальных потерь АФ. Однако при этом следует иметь
ввиду, что своего минимума потери достигают, когда характеристика коэффициента
передачи становится одногорбой, то есть далекой от прямоугольной. Таким
образом, мы имеем противоречие между требованиями минимизации потерь и
прямоугольностью частотной характеристики АФ.
Указанное противоречие находит
отражение также в поведении ширины полосы запирания и крутизны скатов. Из рис.
13 видно, что параметр ![]() увеличивается с ростом
электрической длины
увеличивается с ростом
электрической длины ![]() . При этом, как следует из рис. 14, на котором
показана зависимость крутизны скатов
. При этом, как следует из рис. 14, на котором
показана зависимость крутизны скатов ![]() от величины
от величины ![]() , при увеличении связи
АФ со схемой ее частотная характеристика становится более пологой, что
выражается в уменьшении параметра
, при увеличении связи
АФ со схемой ее частотная характеристика становится более пологой, что
выражается в уменьшении параметра ![]() .
.

Рис. 13. Зависимость ширины полосы запирания антенны-фильтра от уровня связи с внешней схемой.
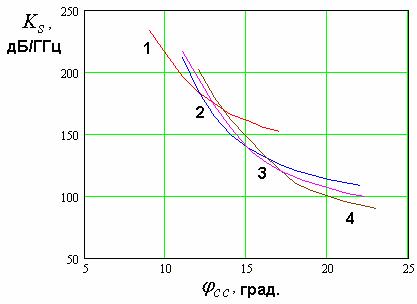
Рис. 14. Зависимость крутизны скатов частотной характеристики антенны-фильтра от уровня связи с внешней схемой.
Результаты численных расчетов,
которые представлены на рис. 10-14, показывают, что настройка фильтра, которая
следует из классической теории [1], не является оптимальной. Например, в
соответствии с этой теорией добротности связи крайних резонаторов с внешней
схемой должны быть одинаковы. В нашем случае это означает, что ![]() . Оценить величину
добротности связи можно с помощью рис. 15, на котором показана ее зависимость
от электрической длины
. Оценить величину
добротности связи можно с помощью рис. 15, на котором показана ее зависимость
от электрической длины ![]() . Также полезным может оказаться график
зависимости добротности связи резонаторов
. Также полезным может оказаться график
зависимости добротности связи резонаторов ![]() от параметра
от параметра ![]() , показанный на
рис. 16. Под добротностью связи резонаторов понимается величина обратная их
коэффициенту связи
, показанный на
рис. 16. Под добротностью связи резонаторов понимается величина обратная их
коэффициенту связи ![]() :
:
![]() . Коэффициент
связи вводится в соответствии с теорией СВЧ фильтров, как отношение расстояния
между собственными частотами системы двух связанных резонаторов
. Коэффициент
связи вводится в соответствии с теорией СВЧ фильтров, как отношение расстояния
между собственными частотами системы двух связанных резонаторов ![]() к средней между ними
частоте
к средней между ними
частоте ![]() .
.
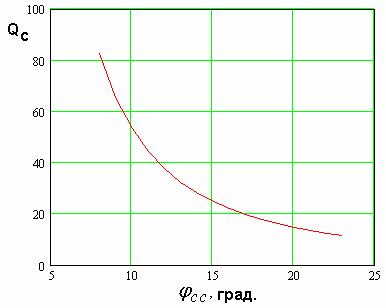
Рис. 15. Зависимость добротности связи резонатора от положения точки включения выходной линии передачи.
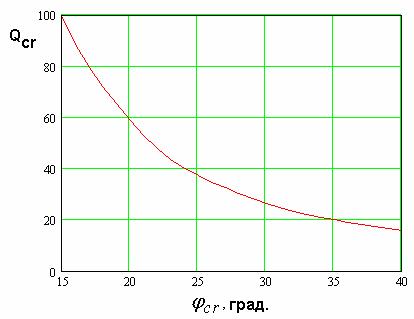
Рис. 16. Зависимость добротности связи двух резонаторов от положения точки их соединения.
Полученные результаты
показывают, что добротность связи в большинстве случаев существенно меньше
радиационной добротности, то есть НР связан со схемой сильнее, чем ПА со
свободным пространством. Также обращает на себя внимание, что оценка потерь АФ
в полосе пропускания (см. раздел 3) совпадает с полученным численным путем
значением потерь лишь для некоторого значения связи НР со схемой. На рис. 17
показаны зависимости потерь в полосе пропускания от параметра ![]() при
при ![]() =25, 27.5, 30,
полученные численным путем (соответственно кривые 1,2,3) и по формуле (6)
(кривые 4,5,6). При этом в формулу (6) подставлялись значения
=25, 27.5, 30,
полученные численным путем (соответственно кривые 1,2,3) и по формуле (6)
(кривые 4,5,6). При этом в формулу (6) подставлялись значения ![]() , определенные по
графикам на рис. 10. Точки пересечения кривых 1-3 и 4-6 позволяют найти
значения
, определенные по
графикам на рис. 10. Точки пересечения кривых 1-3 и 4-6 позволяют найти
значения ![]() , при которых имеется равенство
потерь, определенных разными способами. По этим величинам
, при которых имеется равенство
потерь, определенных разными способами. По этим величинам ![]() из рис. 11 можно
найти неравномерность частотной характеристики. В результате получаем, что
оценка (6) совпадает с численными данными при
из рис. 11 можно
найти неравномерность частотной характеристики. В результате получаем, что
оценка (6) совпадает с численными данными при ![]() 0.17-0.18 дБ вне зависимости от значения
параметра
0.17-0.18 дБ вне зависимости от значения
параметра ![]() . Для больших значений
неравномерности она дает заниженные, а для меньших завышенные результаты.
. Для больших значений
неравномерности она дает заниженные, а для меньших завышенные результаты.
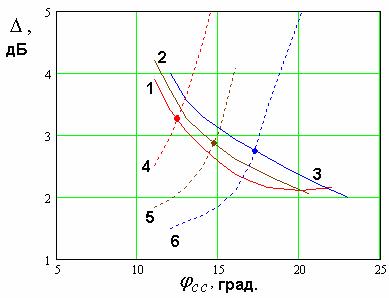
Рис. 17.
Зависимость потерь в полосе пропускания от параметра ![]() .
.
Таким образом, настройка параметров АФ в соответствии с теорией [1] далеко не всегда приводит к оптимальному результату. Наиболее вероятно это связано с существенным влиянием тепловых потерь на частотную характеристику АФ, так как классический подход основан на предположении, что параметры реального фильтра несущественно отличаются от параметров фильтра с потерями.
В этой связи становится актуальной задача разработки методики экспериментальной (включая численный эксперимент) настройки АФ, которая позволила бы приблизиться за минимальное число шагов к требуемой частотной характеристике устройства.
5. Электродинамическая модель АФ
Следующий этап исследования АФ заключается в построении численной электродинамической модели. С ее помощью можно учесть практически все факторы, характерные для реального устройства. Такая модель была построена для АФ с щелевой связью (см. рис. 1 б). Модель, показанная на рис. 18, создавалась в системе High Frequency System Simulator (HFSS).
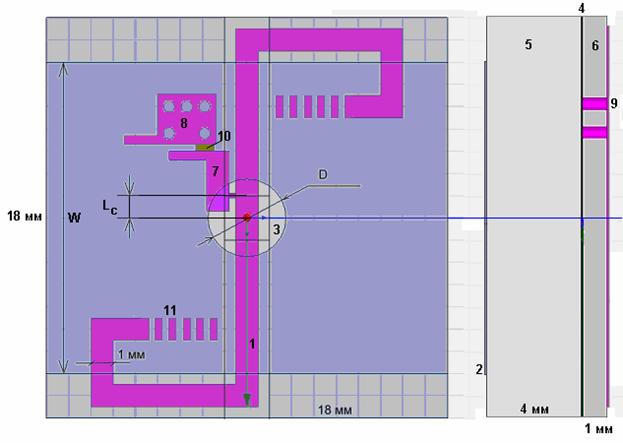
Рис. 18. Модель антенны-фильтра для численного исследования.
Параметры антенны выбирались в соответствии с параметрами
образца, который впоследствии исследовался экспериментально. При этом они
естественным образом разделились на две группы: фиксированные и свободные.
Фиксированные параметры не могут изменяться в ходе настройки устройства. На
рис. 18 даны их конкретные числовые значения. Настройку можно осуществлять
только с помощью свободных параметров, которые на рис. 18 имеют буквенные
обозначения. К их числу относятся: длина ПА ![]() , расстояние от центра НР до точки
подключения внешней нагрузки
, расстояние от центра НР до точки
подключения внешней нагрузки ![]() , диаметр отверстия связи
, диаметр отверстия связи ![]() .
.
Модель, показанная на рис. 18, состоит из следующих
элементов. НР выполнен в виде микрополоскового резонатора и состоит из
проводника 1, расположенного на диэлектрической подложке 6 толщиной 1 мм.
Проницаемость подложки равна 10. ПА выполнена на подложке 5 толщиной 4 мм с
проницаемостью равной 40. НР и ПА имеют общий экран 4, в котором выполнено
круглое отверстие связи 3. Внешняя нагрузка моделируется сосредоточенным портом
10, который включен между контактными площадками 7 и 8. Площадка 7 соединяется
с проводником 1 тонкой перемычкой, расположение которой задает длину ![]() . Площадка 8 соединяется
с экраном 4 с помощью металлизированных отверстий 9.
. Площадка 8 соединяется
с экраном 4 с помощью металлизированных отверстий 9.
Целью методики, о которой говорилось в разделе 4, является
выбор свободных параметров, обеспечивающих форму частотной характеристики АФ с
требуемой степенью прямоугольности и нужным уровнем потерь. Многократные
численные расчеты и эксперименты позволили сформулировать следующую
последовательность шагов, выполнение которых приводит к достижению поставленной
цели. Шагом, который можно назвать нулевым, является выбор диаметра отверстия
связи ![]() . Далее
следуют три этапа.
. Далее
следуют три этапа.
1. Настройка
НР на заданную частоту ![]() . Рассматривается один НР. Для этого ПА
либо удаляется из модели, либо настраивается выбором длины
. Рассматривается один НР. Для этого ПА
либо удаляется из модели, либо настраивается выбором длины ![]() на частоту, которая будет
достаточно сильно отличаться от
на частоту, которая будет
достаточно сильно отличаться от ![]() . Настройка НР производится при наличии
отверстия связи. Связь с внешней схемой устанавливается выше критической
(присутствие в модели отверстия связи и сильной связи с внешней нагрузкой
необходимо для учета их влияния на резонансную частоту НР). Настройка
резонансной частоты производится с помощью перемычек, соединяющих площадки 11 с
проводником 1. Типичная частотная зависимость модуля коэффициента отражения
. Настройка НР производится при наличии
отверстия связи. Связь с внешней схемой устанавливается выше критической
(присутствие в модели отверстия связи и сильной связи с внешней нагрузкой
необходимо для учета их влияния на резонансную частоту НР). Настройка
резонансной частоты производится с помощью перемычек, соединяющих площадки 11 с
проводником 1. Типичная частотная зависимость модуля коэффициента отражения ![]() от входа АФ с ПА
настроенной ниже НР показана на рис. 19. Резонансам ПА и НР соответствуют
провалы
от входа АФ с ПА
настроенной ниже НР показана на рис. 19. Резонансам ПА и НР соответствуют
провалы ![]() .
Минимум 1 соответствует резонансу НР, а минимум 2 резонансу ПА. То
обстоятельство, что провал, порожденный ПА, глубже аналогичного провала НР,
обусловлено выбором связи с внешней схемой, которая, как уже говорилось,
установлена выше критической.
.
Минимум 1 соответствует резонансу НР, а минимум 2 резонансу ПА. То
обстоятельство, что провал, порожденный ПА, глубже аналогичного провала НР,
обусловлено выбором связи с внешней схемой, которая, как уже говорилось,
установлена выше критической.
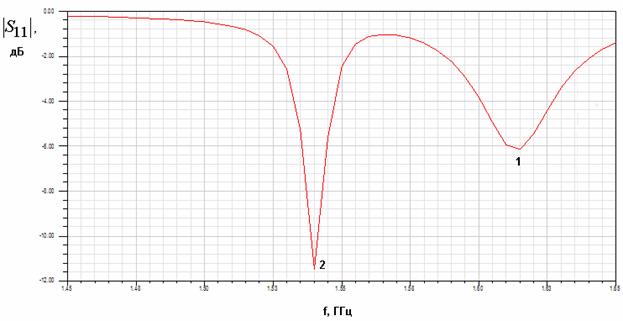
Рис. 19. Частотная зависимость модуля коэффициента отражения от антенны-фильтра на первом этапе ее настройки.
2. Настройка
частоты ПА. На этом этапе изменяется размер ПА - ![]() , определяющий ее резонансную частоту. При
этом собственные частоты ПА и НР сближаются. Одним из возможных критериев их
равенства является симметрия расположения провалов коэффициента отражения
относительно центральной частоты
, определяющий ее резонансную частоту. При
этом собственные частоты ПА и НР сближаются. Одним из возможных критериев их
равенства является симметрия расположения провалов коэффициента отражения
относительно центральной частоты ![]() . На рис. 20 показана типичная частотная
зависимость коэффициента стоячей волны (КСВ) АФ, которая получается в
результате настройки ПА.
. На рис. 20 показана типичная частотная
зависимость коэффициента стоячей волны (КСВ) АФ, которая получается в
результате настройки ПА.
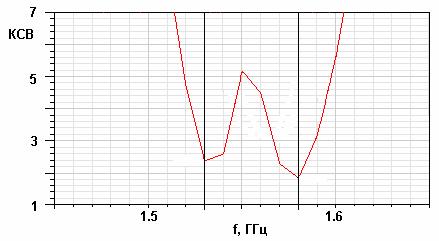
Рис. 20. Частотная зависимость модуля коэффициента отражения от антенны-фильтра на втором этапе ее настройки.
Экспериментальное измерение
коэффициента отражения реализуется более просто, чем измерение характеристик
прохождения. Тем не менее, именно последние представляют большую ценность с
практической точки зрения. Поэтому целесообразнее использовать в качестве
критерия настройки АФ симметрию частотной характеристики коэффициента передачи
АФ. На рис. 21 показана расчетная зависимость коэффициента передачи по мощности
![]() из АФ в
тестовую вибраторную антенну. Отметим, что этот параметр пропорционален
введенному в разделе 2 коэффициенту передачи
из АФ в
тестовую вибраторную антенну. Отметим, что этот параметр пропорционален
введенному в разделе 2 коэффициенту передачи ![]() . Кривые 1-5 соответствуют W=14, 13.2, 13, 12.8, 12.6. Они получены при D=3.8, Lc=0.3.
Видно, что оптимальное значение W находится
между 13 и 12.8. Важно, что критерии, использующие симметрию коэффициента отражения
и коэффициента передачи, дают близкие, но не совсем совпадающие друг с другом
значения длины W.
. Кривые 1-5 соответствуют W=14, 13.2, 13, 12.8, 12.6. Они получены при D=3.8, Lc=0.3.
Видно, что оптимальное значение W находится
между 13 и 12.8. Важно, что критерии, использующие симметрию коэффициента отражения
и коэффициента передачи, дают близкие, но не совсем совпадающие друг с другом
значения длины W.
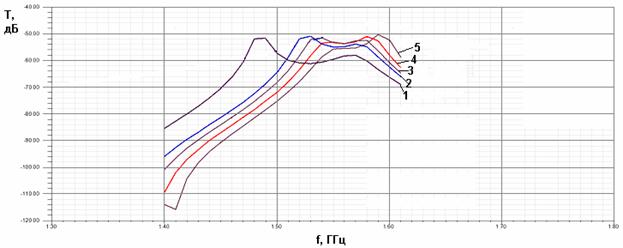
Рис. 21. Частотная зависимость модуля коэффициента передачи при разной длине печатной антенны.
3. Настройка
связи с внешней схемой. На этом этапе подбирается величина ![]() . Пример изменения частотной
характеристики коэффициента передачи
. Пример изменения частотной
характеристики коэффициента передачи ![]() от параметра
от параметра ![]() показан на рис. 22. Кривые 1-9 получены
для
показан на рис. 22. Кривые 1-9 получены
для ![]() =0.1, 0.2,
0.3, 0.4, 0.5, 0.6, 0.8, 1.0, 1.2 при W=12.8, D=4. При увеличении связи с внешней схемой происходит
уменьшение неравномерности частотной характеристики в полосе пропускания и
постепенный переход от двугорбой кривой к одногорбой аналогично случаю,
рассмотренному в разделе 4. Увеличение связи сопровождается также снижением
крутизны частотной характеристики вне полосы проспускания. Из рис. 22 видно,
что кривые 1-9 в достаточной степени симметричны независимо от величины
=0.1, 0.2,
0.3, 0.4, 0.5, 0.6, 0.8, 1.0, 1.2 при W=12.8, D=4. При увеличении связи с внешней схемой происходит
уменьшение неравномерности частотной характеристики в полосе пропускания и
постепенный переход от двугорбой кривой к одногорбой аналогично случаю,
рассмотренному в разделе 4. Увеличение связи сопровождается также снижением
крутизны частотной характеристики вне полосы проспускания. Из рис. 22 видно,
что кривые 1-9 в достаточной степени симметричны независимо от величины ![]() .
.
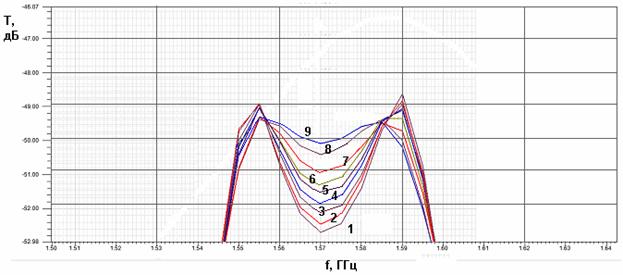
Рис. 22. Частотная зависимость модуля коэффициента передачи при разном положении точки подключения выходной линии передачи.
Результатом выполнения шагов
1-3 является частотная характеристика АФ, соответствующая нужной частоте и
имеющая требуемую форму. Однако она может иметь ширину полосы пропускания,
отличающуюся от требуемой. Для достижения заданного значения полосы пропускания
необходимо изменить диаметр отверстия связи ![]() и повторить для него шаги 1-3. Пример
выполнения первого шага настройки для измененного диаметра отверстия связи
показан на рис. 23. Графики на рис. 23 целесообразно сравнивать с графиками на
рис. 21. Они получены для
и повторить для него шаги 1-3. Пример
выполнения первого шага настройки для измененного диаметра отверстия связи
показан на рис. 23. Графики на рис. 23 целесообразно сравнивать с графиками на
рис. 21. Они получены для ![]() =3.5 (рис. 21 соответствует
=3.5 (рис. 21 соответствует ![]() =3.8). Кривые 1-4
получены при W=12.6, 12.8, 13, 13.2.
=3.8). Кривые 1-4
получены при W=12.6, 12.8, 13, 13.2.
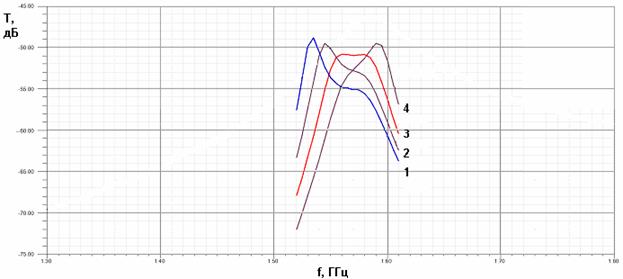
Рис. 23. Частотная зависимость модуля коэффициента передачи при разных размерах отверстия связи.
Достоинством предложенной
методики настройки АФ является то, что мы многократно изменяем те параметры,
которые на практике легко могут быть изменены. В тоже время, такой параметр как
диаметр труднодоступного отверстия связи ![]() варьируется минимальное число раз. Данная
методика многократно использовалась в ходе натурных и численных экспериментов.
варьируется минимальное число раз. Данная
методика многократно использовалась в ходе натурных и численных экспериментов.
6. Экспериментальное исследование АФ
Экспериментально исследовался ряд АФ, предназначенных для
использования в качестве приемных антенн системы спутниковой навигации. Рабочий
диапазон АФ 1572-1612 МГц. Все антенны работали с линейно поляризованными
волнами. Две из них были выполнены по схеме, показанной на рис. 1 б и одна по
схеме, соответствующей рис. 1 в. Две антенны с щелевой связью отличались
диэлектрической проницаемостью ![]() материала, из которого была выполнена ПА
и, следовательно, ее размерами. Одна ПА была выполнена из керамики с
материала, из которого была выполнена ПА
и, следовательно, ее размерами. Одна ПА была выполнена из керамики с ![]() =40 с размерами 18х18х4,
а другая из материала ФЛАН-10 (
=40 с размерами 18х18х4,
а другая из материала ФЛАН-10 (![]() =10) с размерами 40х40х4. Антенна, в
которой НР и ПА расположены на одном уровне (см. рис. 1 в), также была
выполнена из материала ФЛАН-10. Назовем ее однослойной АФ.
=10) с размерами 40х40х4. Антенна, в
которой НР и ПА расположены на одном уровне (см. рис. 1 в), также была
выполнена из материала ФЛАН-10. Назовем ее однослойной АФ.
На рис. 24 а-в показаны фотографии АФ с щелевой связью и ее элементов. На рис. 24 а она изображены со стороны ПА, на рис. 24 б со стороны НР, а на рис. 24 в показан общий металлический экран ПА и НР с отверстием связи круглой формы. Показанная на рис. 24 а-в АФ соответствует модели, обсуждавшейся в разделе 5.
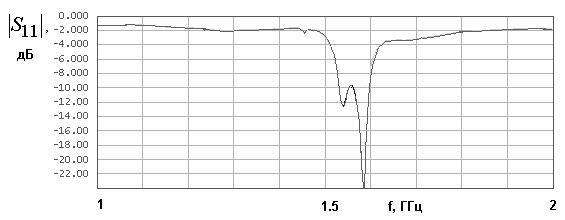
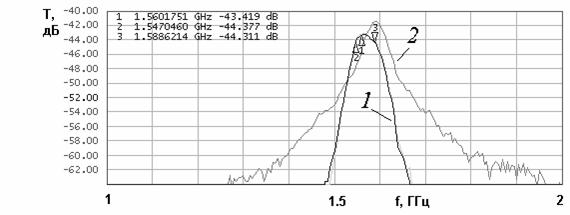
На рис. 25 а,б показаны полученные экспериментально
частотные характеристики АФ с щелевой связью и ПА из керамики с ![]() =40. Диаметр отверстия
связи в экспериментальном образце равен 3. НР выполнен из материала ФЛАН (
=40. Диаметр отверстия
связи в экспериментальном образце равен 3. НР выполнен из материала ФЛАН (![]() =10). Его топология
показана на рис. 18. Частотная зависимость модуля коэффициента отражения от
входа АФ показана на рис. 25 а. На рис. 25 б представлена частотная зависимость
модуля коэффициента передачи из рупорной антенны в АФ. Антенны устанавливались
на расстоянии 2.5 м. Кривая 1 соответствует исследуемой АФ, а кривая 2 -
стандартной антенне, разработанной для приема сигналов систем спутниковой
навигации GPS и ГЛОНАС (разработчик – фирма Trimble). Отметим, что кривые 1 и 2 на рис. 26 и 27 также
соответствуют АФ и стандартной антенне.
=10). Его топология
показана на рис. 18. Частотная зависимость модуля коэффициента отражения от
входа АФ показана на рис. 25 а. На рис. 25 б представлена частотная зависимость
модуля коэффициента передачи из рупорной антенны в АФ. Антенны устанавливались
на расстоянии 2.5 м. Кривая 1 соответствует исследуемой АФ, а кривая 2 -
стандартной антенне, разработанной для приема сигналов систем спутниковой
навигации GPS и ГЛОНАС (разработчик – фирма Trimble). Отметим, что кривые 1 и 2 на рис. 26 и 27 также
соответствуют АФ и стандартной антенне.


а б

в
Рис. 24. Макет двухслойной антенны-фильтра.
Из рис. 25 а,б видно, что данная АФ имеет одногорбую частотную характеристику коэффициента передачи, что соответствует сильной связи АФ с внешней схемой. Максимальное значение коэффициента передачи на 2 дБ меньше, чем у стандартной антенны. Также из рис. 25 б видно, что АФ имеет существенно большую крутизну скатов частотной характеристики.
а
б
Рис. 25. Частотные характеристики модулей коэффициентов отражения и передачи двухслойной антенны-фильтра.
Графики на рис. 26 получены для однослойной АФ (НР и ПА расположены в одной плоскости). Кривая 1 имеет выраженный двугорбый характер. Данная АФ настроена не вполне оптимально, так как ее коэффициент передачи в точках максимумов имеет разные значения, отличающиеся на 1.5 дБ. Средняя между ними величина примерно на 1 дБ меньше максимального коэффициента передачи стандартной антенны.
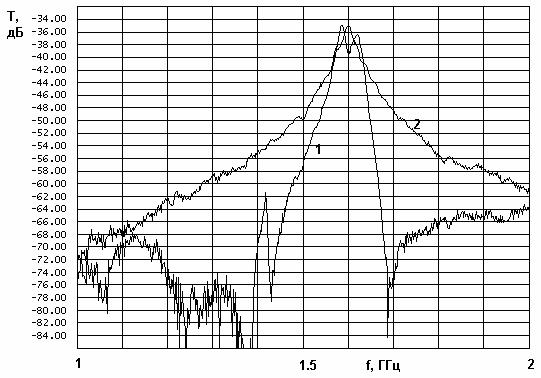
Рис. 26. Частотная характеристика модуля коэффициента передачи двухслойной антенны-фильтра.
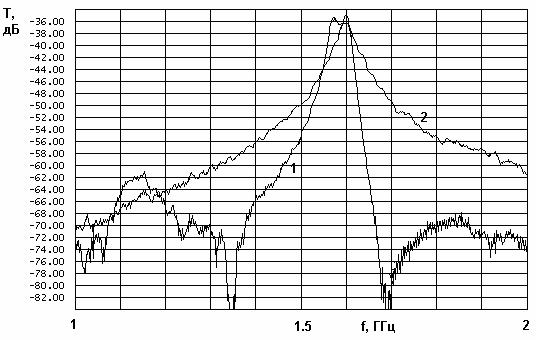
На рис. 27 а,б представлены экспериментальные данные для АФ с щелевой связью, у которой ПА выполнена из материала ФЛАН. На рис. 27 а показана частотная зависимость модуля коэффициента отражения, а на рис. 27 б частотная зависимость коэффициента передачи. Данная АФ имеет частотную характеристику, близкую к прямоугольной. Потери по отношению к стандартной антенне составляют величину около 1 дБ.

а
б
Рис. 27. Частотные характеристики модулей коэффициентов отражения и передачи однослойной антенны-фильтра.
Из рис. 26 и 27 б видно, что вблизи полосы пропускания АФ обеспечивает большую крутизну частотной характеристики, чем стандартная антенна. На большом удалении от полосы пропускания это преимущество исчезает. Такое поведение коэффициента передачи во многом обусловлено влиянием особенностей конструктивной реализации АФ. Большое значение имеет экранировка НР. Его излучение мало по сравнению с излучением ПА в пределах полосы пропускания АФ. Вне ее оно становится сопоставимым с излучением ПА, что приводит к существенному увеличению коэффициента передачи АФ. В полном объеме вопрос о конструктивной реализации АФ в рамках данной работы не рассматривался.
Литература
1. Маттей Д.Л. Янг Л. Джонс Е.М.Т. Фильтры СВЧ, согласующие цепи и цепи связи. Т. 1. М.: Связь, 1971.
2. Диденко А.Н. Сверхпроводящие волноводы и резонаторы. М.: Сов. Радио, 1973.
3. Банков С.Е., Курушин А.А., Разевиг В.Д. Анализ и оптимизация трехмерных СВЧ структур с помощью HFSS. М.: Солон-Пресс, 2004.
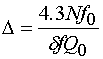 , дБ (6)
, дБ (6)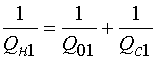 . (7)
. (7)