Применение метода смешанных конечных элементов для вычисления мод цилиндрических волноводов с переменным показателем преломления

УДК 517.95

А. Л. Делицын¹, С. И. Круглов²

¹ физический факультет МГУ имени М.В. Ломоносова, кафедра математики

² МИРЭА, кафедра прикладной математики

Получена 7 апреля 2012 г.

Аннотация. Метод смешанных конечных элементов применяется к задаче вычисления мод цилиндрических волноводов с переменным заполнением. Для решения проблемы аппроксимации поля в нуле введен идеально проводящий цилиндр малого радиуса, расположенный на оси волновода. Приведены результаты тестирования, показывающие высокую точность применяемого подхода. Рассмотрены возможности метода при решении задач с переменным показателем преломления.

Ключевые слова: дисперсионные кривые, волноводы, смешанные конечные элементы.

Abstract. Mixed finite elements are applied to cylindrical waveguides with arbitrary filling mode computation. For the solution of the field approximation problem in the zero point the ideal conductor is introduced to the waveguide axis. Test results have high accuracy. The method opportunities are considered for the problems with arbitrary filling.

Keywords: dispersion curves, waveguides, mixed finite elements.

Результаты вычислений спектральных характеристик волноводов с переменным показателем преломления показывают сложное поведение их

дисперсионных кривых и возможность существования как вещественных, так и комплексных мод, несмотря на отсутствие потерь в среде, заполняющий волновод. Примеры возникновения подобных волн приведены в достаточно большом количестве работ. (см. [1] и приведенную там библиографию). В то же время следует заметить, что общая математическая теория, описывающая с качественной точки зрения характер дисперсионных кривых волноводов с произвольным изменением показателя преломление, пока отсутствует. Основное внимание уделялось расчету и подробному исследованию конкретных систем, например двухслойному волноводу (см. [1]).

Дополнительное усложнение возникает в случае, если диэлектрическая проницаемость, в общем случае комплексная, имеет отрицательную вещественную часть. Подобные задачи рассматриваются как феноменологические модели, описывающие метаматериалы. В этом случае, даже простейшие системы, такие как диэлектрический слой, приводят к сложной картине дисперсионных кривых [2]. В большом количестве работ, посвящённых вычислению спектральных характеристик слоистых волноводов , используется метод сшивания мод, сводящий исходную задачу к решению дисперсионного уравнения. Несмотря на очевидные достоинства метода и его высокую точность, ему присущи определённые ограничения. Во-первых, метод не очень хорошо применим к случаю волноводов с плавным изменением показателя преломления. Кроме того, исходная линейная спектральная задача сводится к решению нелинейного уравнения, которое требует его отдельного решения для каждой дисперсионной кривой.

В настоящей работе рассматривается применение метода смешанных конечных элементов для решения спектральной задачи для цилиндрических волноводов с переменным показателем преломления, зависящего от радиальной переменной. Исходная линейная спектральная задача для дифференциального оператора сводится к линейной спектральной матричной задаче [3]. В настоящее время для матриц небольшого размера вычисление всех собственных значений и собственных векторов может считаться решенной проблемой, которая с помощью стандартных пакетов, таких как MATLAB решается в режиме «черного ящика», требуя незначительных временных затрат. Следует заметить, что при необходимости, возможно значительное увеличение эффективности решения спектральной задачи, учитывая ленточный характер матриц дискретной задачи на собственные значения.

С помощью применяемого подхода возможен расчёт довольно большого количества дисперсионных кривых с достаточно произвольным профилем показателя преломления. Целью настоящей работы является демонстрация возможностей метода. Анализ поведения дисперсионных кривых представляет собой сложную самостоятельную проблему и не рассматривается в настоящей работе.

1.1. Постановка задачи.

Для постановки задачи следуем подходу, применяемому в работах авторов [3-4]. Рассмотрим цилиндрический волновод с круговым поперечным сечением единичного радиуса r = 1. В некоторую точку на его оси поместим цилиндрическую систему координат, ось Oz которой направим по оси цилиндра. Пусть волновод заполнен веществом с характеристикой:

- кусочно-непрерывна в , а стенки волновода являются идеально проводящими.

Электромагнитное поле внутри волновода описывается системой из восьми уравнений Максвелла для шести неизвестных:

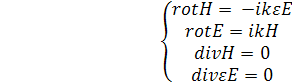(1)

Раскроем уравнения и перепишем их в цилиндрической системе координат:

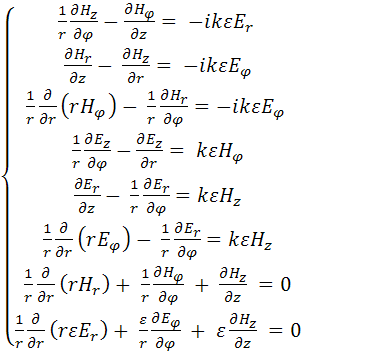(2)

Будем искать решение в виде нормальных волн, то есть функций имеющих зависимость от r, z, вида E, H = .

Подставим их в (2), сократим на экспоненциальный множитель и придём к задаче на собственные значения на отрезке [0,1], роль собственного значения играет параметр :

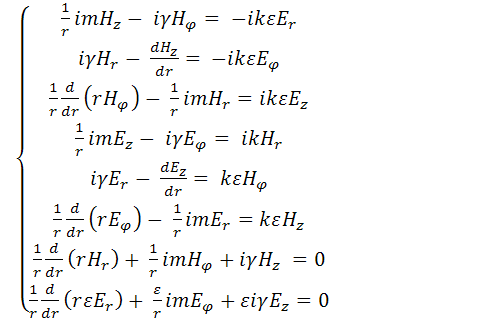(3)

Для постановки задачи выберем следующие уравнения:

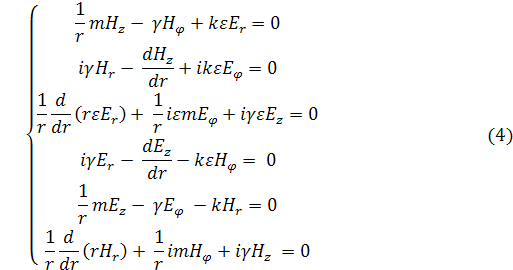
в каждое из которых входит γ.

Введём следующие обозначения:

X = = Y = )^T =

Подставим Y из первых трёх уравнений (4) в следующие три уравнения (4) и придём к задаче на собственные значения:

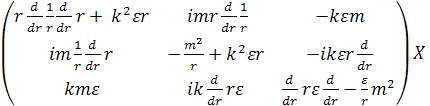
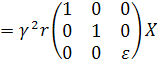(5)

где X удовлетворяет граничным условиям:

H_r(0) = 0 и E_z(0) = 0

H_r(1) = 0 и E_z(1) = 0,

(6)

и неиспользованному выше уравнению Максвелла:

В случае разрывного необходимо задать условия сопряжения на линии разрыва:

_s= _s = 0, _s = _s = 0

1.2. Слабая постановка задачи.

Рассмотрим слабую постановку исходной задачи. Умножим уравнение (5) на произвольный вектор = () и проинтегрируем по r в пределах от 0 до 1. В итоге получаем:

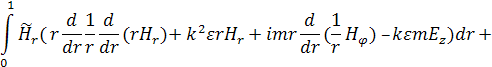
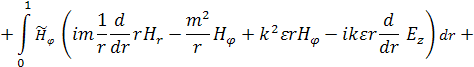(7)

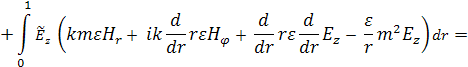
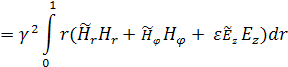
Далее, используя граничные условия, проинтегрируем (7) по частям:

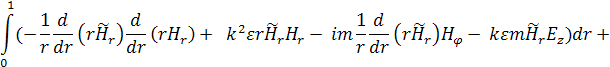
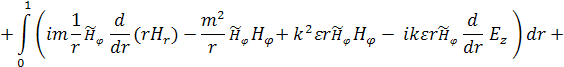
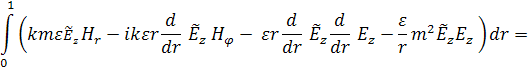
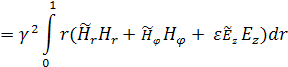
Произведём следующие замены:

В итоге получим:

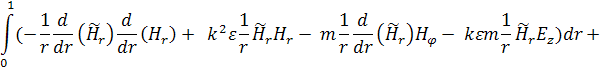
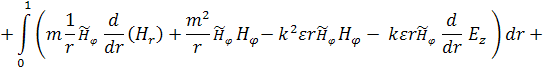(8)

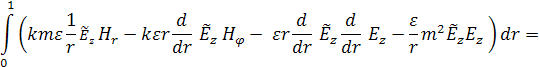
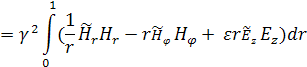
Задача (8) имеет особенность в нуле. Для того, чтобы избежать проблемы описания поля в нуле, на оси волновода расположим тонкий проводящий цилиндр радиуса , и будем рассматривать область ≤r≤1 :

Уравнение примет вид:

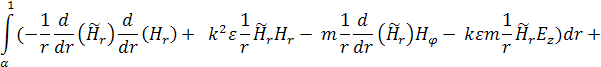
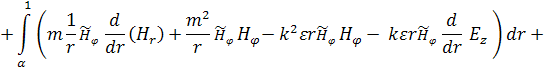(9)

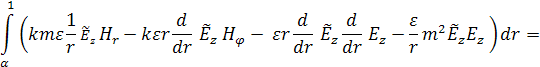
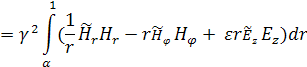
Устремим к нулю. Как следует из легко проверяемого аналога теоремы Самарского, собственные значения задачи (9) будут стремиться к собственным значениям исходной задачи (8).

Итак, задача заключается в поиске собственных значений - постоянных распространения и построения дисперсионных кривых – зависимостей постоянной распространения от волнового числа k.

1.3. Метод смешанных конечных элементов.

Задача (5) имеет бесконечномерное ядро следующего вида:

X = ()

где - произвольная функция, обращающаяся в ноль на границе области.

При применении стандартного метода конечных элементов ядро оператора неправильно аппроксимируется, что приводит к возникновению нефизических решений, так называемых «духов», которые расположены среди истинных значений. Одни из способов избежать этой проблемы, применить метод смешанных конечных элементов [3]. Метод смешанных конечных элементов заключается в аппроксимации компонент вектора X полиномами разных порядков.

Введём на отрезке r [] равномерную сетку . = , =1,

i = 0,1, … n, где n – количество конечных элементов, то есть отрезков, на которые разбивается исходный отрезок, h – длина конечного элемента, или шаг сетки, таким образом: , k = 0,1.. n-1.

Будем для простоты считать диэлектрическую проницаемость постоянной на каждом конечном элементе:

, при r []

Далее разложим по базисным функциям компоненты векторов Х:

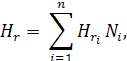
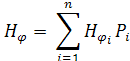
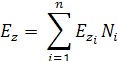
В качестве пробных функций используем:

, , где

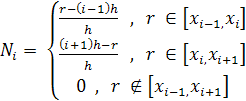
Метод смешанных конечных элементов позволяет правильно аппроксимировать ядро оператора, которое переходит в нулевое собственное значение, кратность которого составляет примерно одну треть от размерности матричной задачи на собственные значения.

Перепишем уравнение следующим образом:

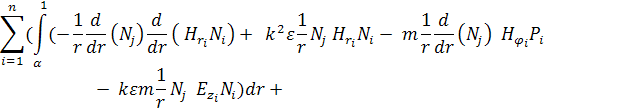
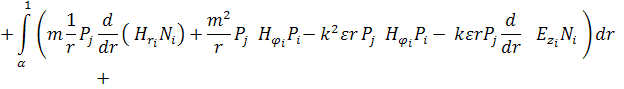(10)

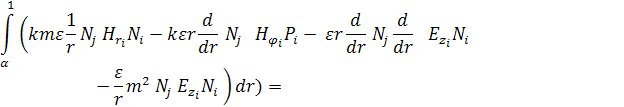
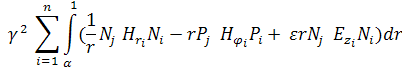
Таким образом, получим обобщённую задачу на собственные значения следующего вида:

AX = BX

1.4. Приложение. Формулы для вычисления элементных матриц.

Укажем формулы для элементов матрицы , соответствующей одному конечному элементу.

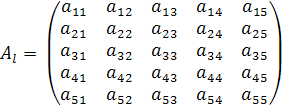
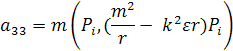
Аналогично для матрицы B:

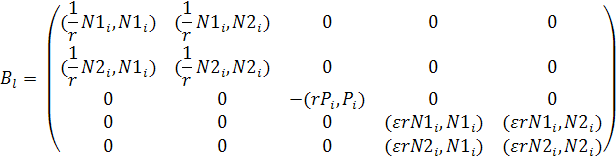
Результаты тестирования

2.1. Общая информация.

Для расчётов по указанному методу была написана программа в системе MATLAB 2009. Данная программа позволяет вычислять собственные значения – постоянные распространения цилиндрических волноводов в зависимости от волнового числа k, а так же от номера моды волновода m для различных профилей .

С помощью разработанной программы можно строить дисперсионные кривые – графики, на которых отражена зависимость постоянной распространения от волнового числа. Решение задачи на собственные значения осуществляются в MATLAB методами вычислительной линейной алгебре, что позволяет при фиксированном k вычислять любое число постоянных распространения, допускаемое порядком матрицы.

Тесты проводились для 200 конечных элементов, при радиусе внутреннего стержня = , остальные параметры указаны в тестовой таблице.

2.2. Случай полого волновода.

Рассмотрим волновод с постоянным показателем преломления ,

m = 1. В таблице 1 приведены результаты расчета постоянной распространения для низших мод в зависимости от волнового числа k. В скобках указаны точные значения.

Таблица 1

K	Imγ ,	Reγ ,	Imγ ,	Reγ ,
0	1.841195 (1.841183)	0	3.831731 (3.831706)	0
0.5	1.772004 (1.771992)	0	3.798969 (3.798943)	0
1	1.545962 (1.545948)	0	3.698941 (3.698914)	0
1.5	1.067707 (1.067688)	0	3.525927 (2.525900)	0
2	0	0.781025 (0.781051)	3.268358 (3.268328)	0
2.5	0	1.691153 (1.691165)	2.903819 (2.903785)	0
3	0	2.368543 (2.368552)	2.383727 (2.383688)	0
3.5	0	2.976575 (2.976582)	1.559540 (1.559478)	0
4	0	3.551056 (3.551062)	0	1.147968 (1.148054)
4.5	0	4.106092 (4.106098)	0	2.359625 (2.359667)
5		4.648655 (4.648660)	0	3.212113 (3.212168)

Максимальная относительная погрешность составляет 0.0026%.

Отсюда можно сделать вывод о том, что данный метод позволяет рассчитывать постоянные распространения цилиндрических волноводов с достаточно высокой точностью.

2.3. Двухслойные волноводы.

Гибридные волны в двухслойных волноводах обладают рядом известных особенностей, которые отсутствуют у волн однородно заполненных волноводов. Им присущи образования аномальной дисперсии, а так же образование встречных потоков мощности. При некоторых конкретных параметрах волны могут преобразовываться в волны с комплексными постоянными распространения – так называемые комплексные волны, даже при отсутствии диссипации энергии в волноводах.

Рассмотрим двухслойный волновод со следующим профилем заполнения:

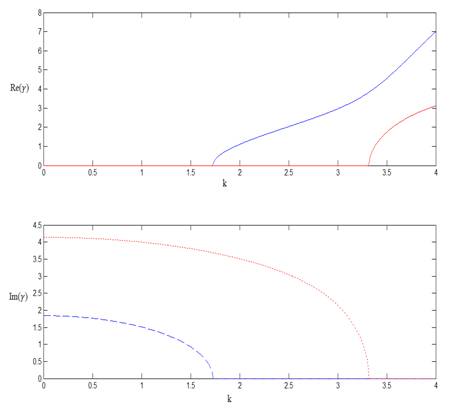
Рис.1.

На рисунке 1 представлены дисперсионные характеристики волн цилиндрического волновода с диэлектрическим стрежнем () радиуса

r = 0.2. Видно, что постоянные распространения или действительны или чисто мнимы. Никаких аномалий не наблюдается, что полностью согласуется с известными результатами [1].

Далее рассмотрим волновод с диэлектрическим стержнем ()

радиуса r = 0.6.

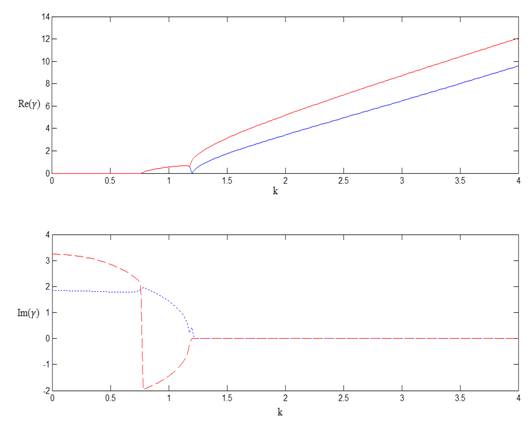
Рис.2.

На рисунке 2 наблюдаются аномальные волны – возникновение комплексных значений постоянной распространения. Следует отметить, что все результаты с графической точностью совпадают с результатами, приведенными в работе [1].

2.4. Шестислойный волновод. Дисперсионные кривые высших порядков

Теперь рассмотрим волновод с более сложным диэлектрическим заполнением, а так же дисперсионные кривые высших порядков.

Данный волновод заполнен веществом со следующим профилем диэлектрической проницаемости (шестислойный волновод)

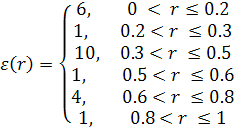
изображенным ниже:

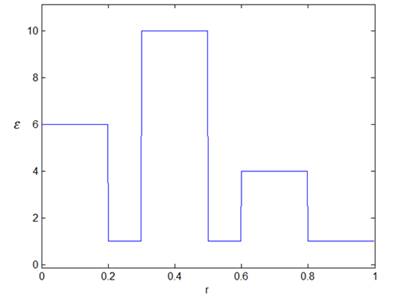
Рис.3.

Для возможности сравнения полученных результатов по точности с результатами, полученными другими методами, мы представим ряд числовых результатов в таблицах, помимо графического представления в виде дисперсионных кривых В таблице 2 указаны значения постоянной распространения 6-слойного волновода для волн низших порядков в зависимости от k. Считаем везде далее в работе m = 1.

Таблица 2

k	Re , HE11	Im , HE11	Re , EH11	Im , EH11
0	0	1.8412	0	2.9042
1	0	1.1533	0	2.1712
2	3.3191	0	1.4437	0
3	6.2895	0	3.3548	0
4	9.3757	0	5.3468	0
5	12.6156	0	8.3128	0
6	15.9291	0	12.0729	0

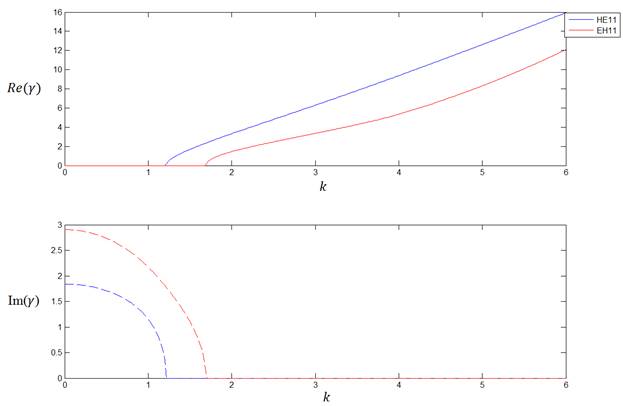
Рис.4.

На рисунке 4 видно, что дисперсионные кривые низших порядков шестислойного волновода не обладают аномалиями, то есть постоянные распространения принимают либо чисто вещественные, либо чисто мнимые значения.

Далее рассмотрим 3-ю и 4-ую дисперсионные кривые шестислойного волновода:

Таблица 3

k	Re , HE12	Im , HE12	Re , EH12	Im , EH12
0	0	5.3316	0	4.6897
1	0	5.0409	0	4.4879
2	0	3.9635	0	3.9082
2.2	0.1168	3.6676	0.1168	- 3.6676
2.4	0.1415	3.3457	0.1415	- 3.3457
2.6	0.0702	2.9494	0.0702	- 2.9494
2.8	0	2.7050	0	2.1589
3	0	2.3130	0	0.8658
4	2.7687	0	4.7804	0
5	5.8219	0	7.3443	0
6	8.9094	0	10.4968	0
7	11.3902	0	13.5473	0
8	14.2025	0	16.4221	0

В таблице 3 приведены результаты расчёта постоянной распространения для 3-ей и 4-ой дисперсионных кривых 6-слойного волновода.

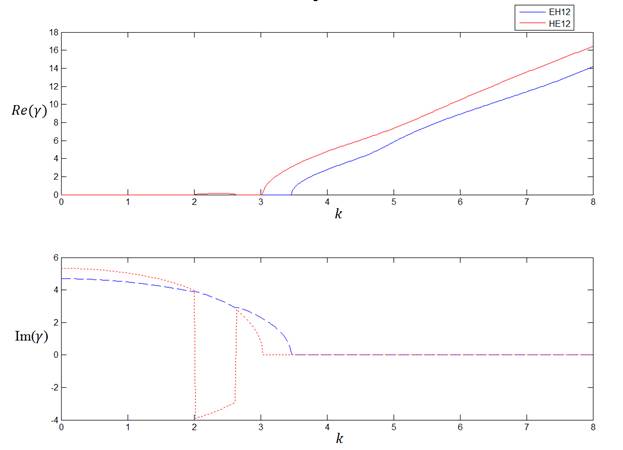
Рис. 5.

На рисунке 5 представлены 3-я и 4-ая дисперсионные кривые шестислойного волновода. Здесь наблюдаются аномалии – возникновение комплексных волн. Следует отметить, что промежуток изменения волнового числа k, где возникли комплексные волны, относительно небольшой. А так же относительно мала вещественная часть этих комплексных волн.

Далее рассмотрим 5-ую и 6-ую дисперсионные кривые шестислойного волновода.

Таблица 4

k	Re , HE13	Im , HE13	Re , EH13	Im , EH13
0	0	8.5369	0	10.4346
1	0	8.2855	0	10.2270
2	0	7.4876	0	9.5414
3	0	5.9580	0	8.2205
4	0	2.6221	0	6.0257
5	5.0449	0	0	1.8112
6	7.1521	0	4.5480	0
7	9.1037	0	8.5557	0
7.1	9.3000	0	9.0216	0
7.2	9.4677	0	9.4990	0
7.3	9.6939	0	9.9018	0
7.4	9.8925	0	10.3168	0
7.5	10.0918	0	10.7158	0
7.8	10.6955	0	11.8142	0
8	11.1032	0	12.4645	0

В таблице 4 указаны значения постоянной распространения для 5-ой и 6-ой дисперсионных кривых 6-слойного волновода. Диапазон частот, на которых происходит пресечение кривых, отражён более подробно. Графически эти результаты представлены на рисунке 6.

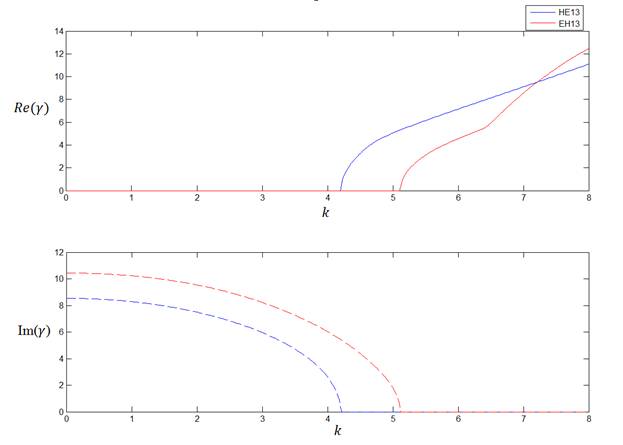
Рис. 6.

На рисунке 6 представлены 5-ая и 6-ая дисперсионные кривые шестислойного волновода. Здесь наблюдается такой эффект, как пересечение или «кроссинг» кривых.

Далее рассмотрим 7-ую и 8-ую дисперсионные кривые шестислойного волновода.

Таблица 5

k	Re , HE14	Im , HE14	Re , EH14	Im , EH14
0	0	11.7076	0	13.3807
1	0	11.5131	0	13.2747
2	0	10.9638	0	12.9303
3	0	10.1120	0	12.1939
4	0	8.8853	0	10.4630
5	0.3681	7.2514	0.3681	-7.2514
5.1	0.4546	6.9517	0.4546	-6.9517
5.2	0.5263	6.6373	0.5263	-6.6373
5.3	0.5877	6.3055	0.5877	-6.3055
5.4	0.6399	5.9528	0.6399	-5.9528
5.5	0.6820	5.5743	0.6820	-5.5743
5.6	0.7099	5.1629	0.7099	-5.1629
5.8	0.6721	4.1892	0.6721	-4.1892
6	0	3.3888	0	2.0395
7	3.7923	0	6.4101	0
8	6.6974	0	8.2029	0

В таблице 5 указаны значения постоянной распространения в зависимости от частоты для 7-ой и 8-ой дисперсионных кривых 6-слойного волновода. Графически это отражено на рисунке 7.

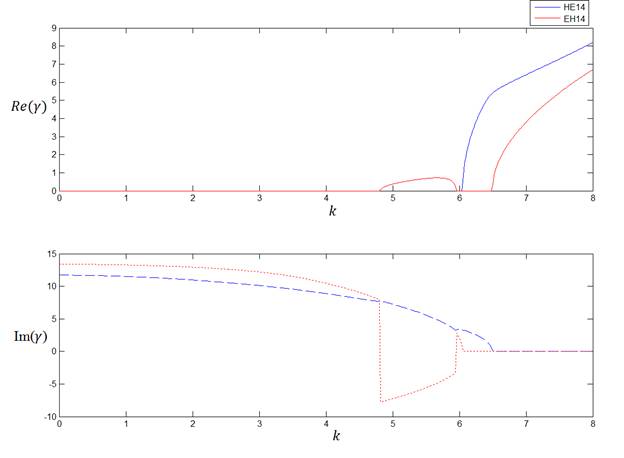
Рис. 7.

На рисунке 7 представлены 7-ая и 8-ая дисперсионные кривые шестислойного волновода. Здесь наблюдается возникновение комплексных волн, причём в значительно большем диапазоне частот, нежели у 3-ей и 4-ой дисперсионных кривых. Так же следует отметить, что вещественная часть у комплексных волн оказывается существенно больше, чем у 3-ей и 4-ой дисперсионных кривых.

В качестве дальнейших примеров рассмотрим применение метода к вычислению дисперсионных кривых волноводов с отрицательной вещественной частью диэлектрической проницаемости. Подобные феноменологические модели рассматриваются в настоящее время как возможные для описания метаматериалов [2].

Рассмотрим двухслойный волновод с радиусом внутреннего стержня r = 0.6 и диэлектрической проницаемостью равной -2 + 0.01i. Ниже приведены графики первых 4 дисперсионных кривых.

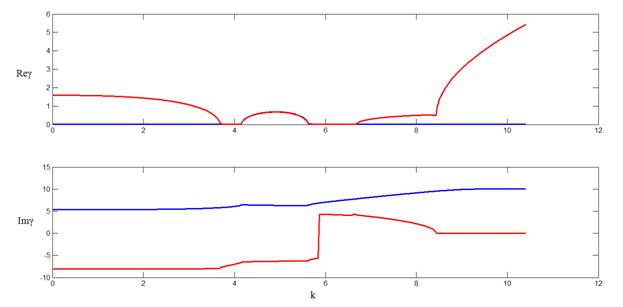
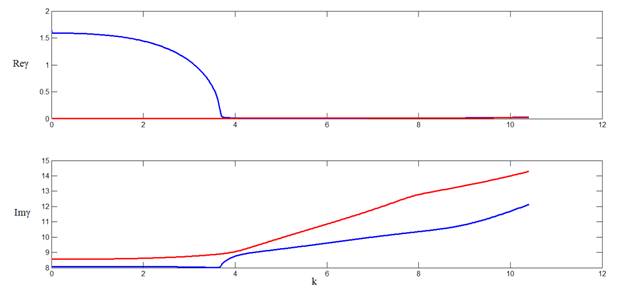
Рис. 8. Дисперсионные кривые волновода с отрицательной вещественной частью диэлектрической проницаемости внутреннего стержня.

В качестве примера приведем первые шесть дисперсионных кривых при ε = -4.

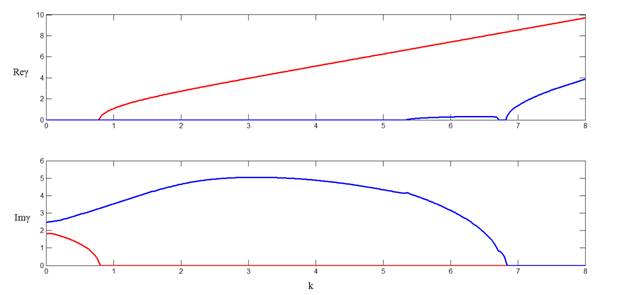
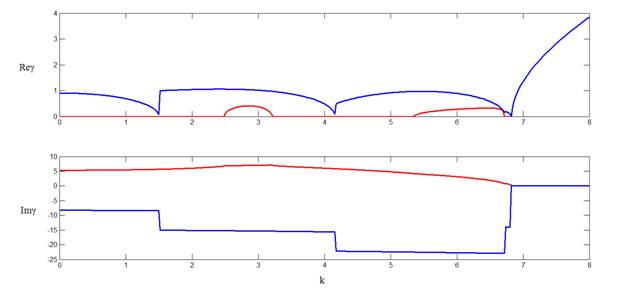
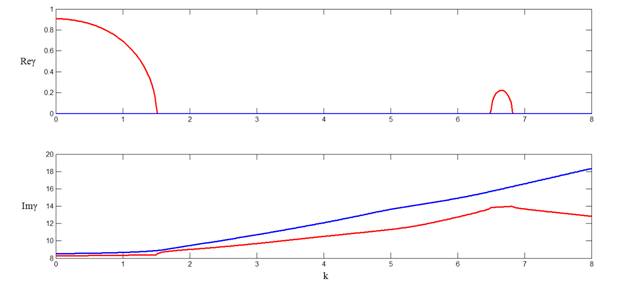
Рис. 9. Дисперсионные кривые волновода с отрицательной вещественной частью диэлектрической проницаемости внутреннего стержня.

Приведенные результаты свидетельствуют о широких возможностях рассматриваемого метода, который может применяться как для анализа спектральных характеристик волноводов с заданным профилем показателя преломления, так и использоваться в качестве программного модуля при решении задач синтеза волноводов с заданными свойствами.

Литература

1. Веселов Г.И., Раевский С.Б. Слоистые металло-диэлектрические волноводы. М.: - Радио и связь, 1988.

2. А. А. Башарин, Н. Л. Меньших. Особенности распространения электромагнитных волн в волноводе из метаматериала с потерями // Журнал радиоэлектроники [электронный журнал]. - 2010. - N 11. - URL: http://jre.cplire.ru/jre/nov10/2/text.pdf

3. Делицын А.Л. О полноте системы собственных векторов электромагнитных волноводов // Журн. вычисл. матем. и матем. физ., Т. 5. N 10. 2011, С. 1883–1888

4. Делицын А.Л. О проблеме применения метода конечных элементов к задаче вычисления мод волноводов // Журн. вычисл. мат. и мат.физики. 1999. т. 39. N 2. С. 315-322.