УДК 517.9 + 621.396.6
МЕТОДЫ ЭЛЕКТРОДИНАМИЧЕСКОГО МОДЕЛИРОВАНИЯ ЭКЛЕКТИЧНЫХ АНТЕННЫХ СИСТЕМ
М. А. Бузова
Филиал ФГУП НИИР-СОНИИР, Самара
Получена 15 марта 2012 г., после
доработки - 13 апреля 2012 г.
Аннотация. Рассмотрены ключевые вопросы построения комбинированных электродинамических методов применительно к анализу антенных систем, содержащих разнотипные антенны и посторонние рассеиватели. На основе комбинированных методов построен общий алгоритм анализа эклектичных антенных систем. Приведены результаты численной проверки предложенного алгоритма.
Ключевые слова: эклектичные антенные системы, комбинированные методы, общий алгоритм.
Abstract. Key problems of creating hybrid electrodynamics methods for antenna systems analysis containing different antennas and scatterers. General algorithm was built based on hybrid methods for analysis eclectic antenna systems. Some numerical results are listed.
Keywords: eclectic antenna systems, hybrid methods, general algorithm.
Введение
Задачи анализа антенных систем, размещаемых в ограниченных условиях пространства и содержащих антенны различных типов и диапазонов, являются весьма интересными и, в то же время, сложными. Интерес они представляют как с теоретической, так и с практической точек зрения. Вполне очевидно, что при таком размещении антенн возникает сложная картина электромагнитного поля, и характеристики антенн существенно изменяются по сравнению с характеристиками в свободном пространстве. Следовательно, возникает проблема внутриобъектовой электромагнитной совместимости. Сложность таких задач заключается, во-первых, в разнообразии форм антенн и рассеивателей, присутствующих в системе. Такое разнообразие означает, что для каждого типа рассеивателя необходимо применение наиболее адекватного метода электродинамического анализа. Во-вторых, сложность решения таких задач заключается в электрически больших размерах рассматриваемых систем. Это приводит к существенным вычислительным затратам, для сокращения которых до разумных пределов используются комбинированные методы на основе объединения строгих и приближенных методов [1].
Для наиболее адекватного описания и электродинамического анализа сложных антенных систем автором было введено понятие эклектичных антенных систем, представляющих собой совокупности тел – рассеивателей электромагнитного поля, разнородных с точки зрения подходов к их электродинамическому анализу [2]. Введенное понятие позволяет охарактеризовать подобные системы, установить взаимосвязь между типом рассеивателя и используемым методом анализа, а также строго учесть взаимодействие между всеми частями системы. Для анализа эклектичных антенных систем автором был разработан общий алгоритм электродинамического анализа [3]. Рассмотрим далее комбинированные методы, входящие в общий алгоритм, а также практический пример применения разработанной теории эклектичных антенных систем.
Комбинированный метод на основе интегральных уравнений Фредгольма первого и второго рода
Большинство антенн диапазонов НЧ – ОВЧ, а также различного рода опоры, мачты, башни представляют собой проволочные конструкции, содержащие проводники различных радиусов. Для их электродинамического анализа традиционно используется тонкопроволочное приближение и метод уравнений Фредгольма первого рода для проводников, радиус которых не превышает 0,01λ (здесь и далее λ – рабочая длина волны антенны), и уравнений Фредгольма второго рода для проводников, радиус которых более 0,01λ. На основе этих двух методов и был разработан комбинированный метод, предназначенный для анализа систем проводников различных радиусов. Общая система уравнений для проволочных систем может быть записана следующим образом:
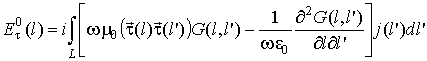 ,
, ![]() , (1)
, (1)
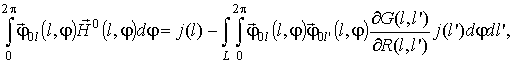 (2)
(2)
![]() ,
,
где i – мнимая единица; ω –
круговая частота; ε0, μ0 – электрическая и магнитная
постоянные; L1, L2 – контуры, соответствующие
тонким и толстым проводникам; L = L1 + L2; ![]() – тангенциальный орт к контурам L1, L2;
– тангенциальный орт к контурам L1, L2; ![]() ,
, ![]() –
азимутальные орты;
–
азимутальные орты; 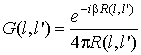 –
функция Грина свободного пространства;
–
функция Грина свободного пространства; ![]() – волновое число;
– волновое число; ![]() – расстояние от точки источника до точки наблюдения;
– расстояние от точки источника до точки наблюдения; ![]() – искомая функция линейного электрического тока;
– искомая функция линейного электрического тока; ![]() – стороннее магнитное поле;
– стороннее магнитное поле; ![]() – тангенциальная компонента стороннего электрического
поля.
– тангенциальная компонента стороннего электрического
поля.
Решение данной системы уравнений стандартными численными методами позволяет найти распределение тока во всей проволочной системе.
Комбинированные методы на основе интегральных уравнений с поверхностным интегралом и физической оптики
В отличие от предыдущего случая в диапазоне СВЧ антенны в большинстве случаев антенны имеют поверхностные электрически протяженные рефлекторы. Кроме этого, на объекте, где устанавливаются антенны, обычно располагаются также посторонние металлоконструкции, представляющие собой поверхностные рассеиватели различной формы и размеров. Посторонние конструкции наряду с подстилающей поверхностью в случае расположения антенн на крыше здания или корпуса автомобиля могут оказывать существенное влияние на характеристики антенн. Поэтому их учет также важен.
Для электродинамического анализа поверхностных рассеивателей наилучшим образом подходят интегральные уравнения (ИУ) с поверхностными интегралами. Однако из-за большого объема затрачиваемых вычислительных ресурсов в подавляющем большинстве случаев использование интегральных уравнений становится невозможным. Поэтому в практических задачах для анализа таких рассеивателей применяются либо квазиоптические методы, такие, как методы физической и геометрической оптики, либо комбинированные методы на основе объединения опять же квазиоптических методов и интегральных уравнений.
В данной работе рассмотрим построение комбинированных методов на основе интегральных уравнений и физической оптики (ФО). Традиционно подобные методы строятся на основе интегральных уравнений первого рода без пересечения областей интегральных уравнений и физической оптики [4]. Автором предлагается строить такие методы на основе интегральных уравнений второго рода с пересечением областей наложения граничных условий.
Интегральные уравнения второго рода с поверхностным интегралом имеют как свои преимущества, так и свои недостатки. К преимуществам этого типа уравнений можно отнести возможность получения разреженной матрицы системы линейных алгебраических уравнений (СЛАУ) при анализе тонких слабо искривленных рассеивателей [5]. В свою очередь, пересечение областей интегральных уравнений и физической оптики в некоторых случаях позволяет увеличить сегмент разбиения в методе интегрального уравнения за счет того, что решение, получаемое с помощью физической оптики, уже близко к истинному решению.
Что же касается недостатков, то наиболее существенным из них является двукратное увеличение области определения искомой токовой функции по сравнению с интегральными уравнениями первого рода при анализе тонких рассеивателей. Для устранения этого недостатка автором было предложено строить интегральные уравнения относительно эквивалентных источников. При этом используются те же общие принципы, что и для тонкопроволочного приближения при анализе проволочных рассеивателей.
Рассмотрим далее основные идеи построения двух комбинированных «токовых» методов на основе интегральных уравнений второго рода.
Первый комбинированный метод строится на основе интегрального уравнения фредгольмовского типа относительно эквивалентного источника. Вводимый эквивалентный ток полагается равным сумме токов, текущих по обеим сторонам рассеивателя, и протекает на воображаемой поверхности, проходящей по середине между реальными поверхностями рассеивателя. Для построения комбинированного метода на основе такого уравнения эквивалентная поверхность рассеивателя S разбивается на две поверхности – SPO и SIE. При этом формально поверхность SPO совпадает с поверхностью S и включает в себя поверхность SIE. На SPO накладывается граничное условие для метода физической оптики, а на SIE – для метода интегральных уравнений. В случае, если в эклектичной системе присутствует несколько протяженных поверхностных рассеивателей, такие поверхности выбираются на каждом рассеивателе.
В результате такого наложения граничных условий и учета взаимного влияния всех областей антенной системы возникает следующая система интегральных уравнений:
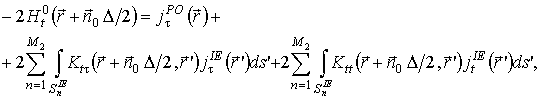 (3)
(3)
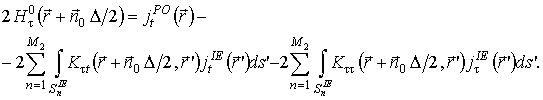 (4)
(4)
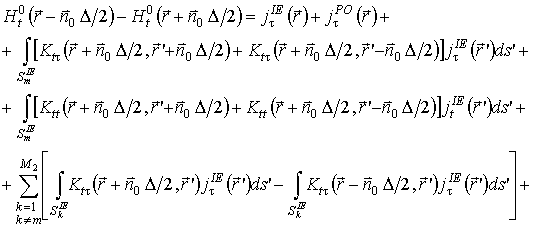 (5)
(5)
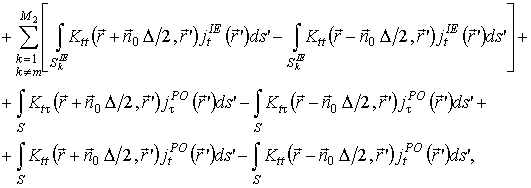
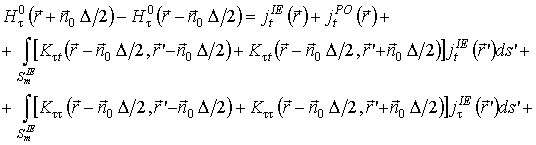 (6)
(6)
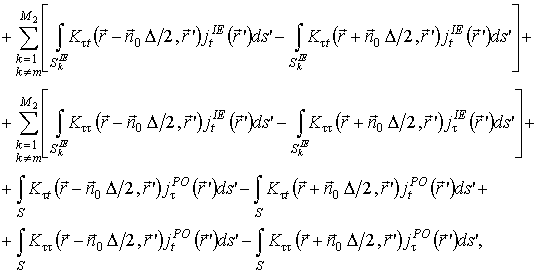
![]() , m = 1, 2, ... M2,
, m = 1, 2, ... M2,
где M2 – число поверхностных
рассеивателей в системе; ![]() –
плотность эквивалентного поверхностного тока в рамках метода интегрального
уравнения;
–
плотность эквивалентного поверхностного тока в рамках метода интегрального
уравнения; ![]() –
плотность эквивалентного поверхностного тока в рамках метода физической оптики;
–
плотность эквивалентного поверхностного тока в рамках метода физической оптики;
![]() – орт внешней
нормали к поверхности; Δ – толщина рассеивателя;
– орт внешней
нормали к поверхности; Δ – толщина рассеивателя;
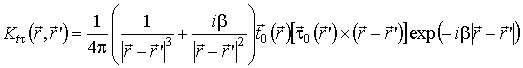 ;
;
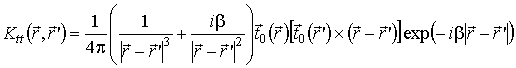 ;
;
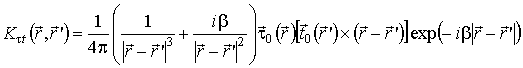 ;
;
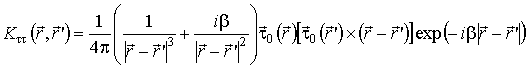 .
.
Уравнения (3), (4) формализуют граничные условия в рамках метода физической оптики, а уравнения (5), (6) – в рамках метода интегрального уравнения. Данные уравнения образуют полную исходную систему уравнений, процедура решения которой составляет содержание разработанного комбинированного метода.
Второй комбинированный метод также строится на основе интегрального уравнения второго рода с точным ядром. Данное уравнение, предложенное автором, строится на основе априорного учета решения, получаемого только методом физической оптики [2]. Это позволяет требовать выполнения граничных условий только на одной стороне рассеивателя, тогда как ток на другой стороне находится с помощью физико-оптического тока. Соответствующий комбинированный метод строится аналогично рассмотренным выше принципам. В результате может быть записана соответствующая система уравнений.
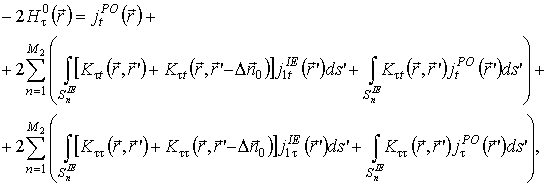 (7)
(7)
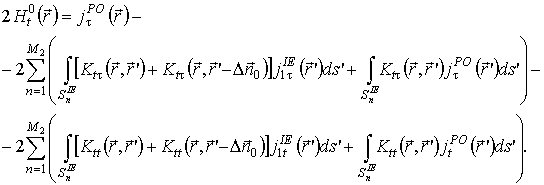 (8)
(8)
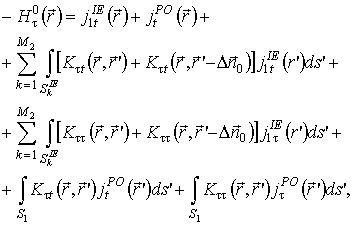 (9)
(9)
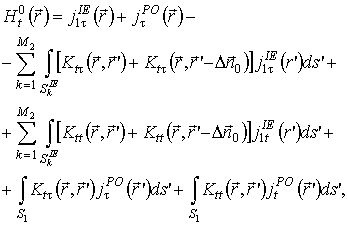 (10)
(10)
Аналогично первому методу уравнения (7), (8) формализуют граничные условия в рамках метода физической оптики, а уравнения (9), (10) – в рамках метода интегрального уравнения.
Общий алгоритм электродинамического моделирования эклектичных антенных систем
Как уже было отмечено выше, полученные уравнения и их системы были объединены в единую систему в рамках общего алгоритма анализа [3]. Система состоит из 10 скалярных уравнений, каждое из которых формализует соответствующее граничное условие. В общем виде данную систему можно записать следующим образом:
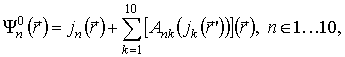 (11)
(11)
где ![]() – функция стороннего электрического или
магнитного поля;
– функция стороннего электрического или
магнитного поля;
![]() – искомая плотность тока;
– искомая плотность тока;
![]() –
операторы соответствующих интегральных уравнений.
–
операторы соответствующих интегральных уравнений.
Отметим, что функция ![]() аддитивно входит только в
интегральные уравнения второго рода и отсутствует в интегральных уравнениях
первого рода. В рамках предлагаемой автором формализации аддитивный член равен
нулю при n = 1, 3, 4.
аддитивно входит только в
интегральные уравнения второго рода и отсутствует в интегральных уравнениях
первого рода. В рамках предлагаемой автором формализации аддитивный член равен
нулю при n = 1, 3, 4.
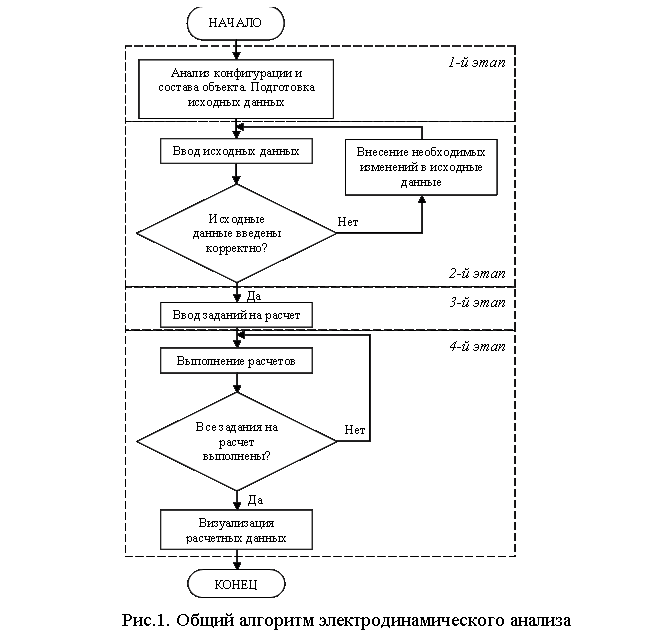
На основе системы (11) построен общий алгоритм электродинамического анализа эклектичных антенных систем. Алгоритм состоит из четырех этапов. Блок-схема алгоритма представлена на рис.1. На первом этапе выполняются анализ конфигурации и состава объекта, а также подготовка исходных данных. На втором этапе осуществляется ввод исходных данных. На третьем этапе осуществляется ввод заданий на расчет. На четвертом этапе алгоритма последовательно выполняется расчет характеристик анализируемой антенной системы в соответствии с каждым введенным заданием, а также визуализация результатов расчетов.
Результаты численных экспериментов с использованием разработанного алгоритма
Для апробации и проверки работоспособности предложенного алгоритма и комбинированных методов, входящих в его состав, были проведены различного рода численные и экспериментальные исследования. В рамках численных исследований выполнялись решение модельных задач и сравнение с решением, полученным известными методами и программными средствами; расчеты эклектичных антенных систем в ограниченных условиях пространства и сравнение полученных результатов с общефизическими закономерностями и теорией антенн; экспериментальные исследования дифракции на проводящих диске и квадратном экране. В данной работе остановимся подробнее на решении модельных задач и сравнении результатов с решениями, полученными известными методами и специализированными программными комплексами.
В качестве модельной рассмотрим задачу дифракции на круглом диске конечной толщины, облучаемом коротким электрическим вибратором, расположенным на оси диска перпендикулярно его поверхности. Преимуществом данной задачи является наличие полной круговой симметрии в системе, что позволяет применять интегральное уравнения даже для протяженных рассеивателей.
В качестве первого примера рассмотрим задачу со следующими геометрическими параметрами: - радиус диска – 5 l (l – длина волны); - толщина экрана – 0,05 l; - линейный размер сегмента разбиения в разработанном комбинированном методе – 0,115 l; - линейный размер сегмента разбиения в известных методах интегральных уравнений первого и второго рода – 0,1 l; - расстояние до вибратора – 1 l; - длина вибратора – 0,1 l; - ширина полосы у кромки экрана, отведенной в область интегрального уравнения в рамках комбинированного метода – 1 l; - радиус круговой площадки в центре экрана, отведенной в область интегрального уравнения в рамках комбинированного метода – 0,5 l.
Решение данной задачи выполнялось разработанным комбинированным методом на основе интегрального уравнения относительно эквивалентного источника, а также с помощью известных интегральных уравнений первого и второго рода, метода физической оптики, специализированных программных пакетов FEKO Suite 5.4, CST STUDIO Suite 2009.
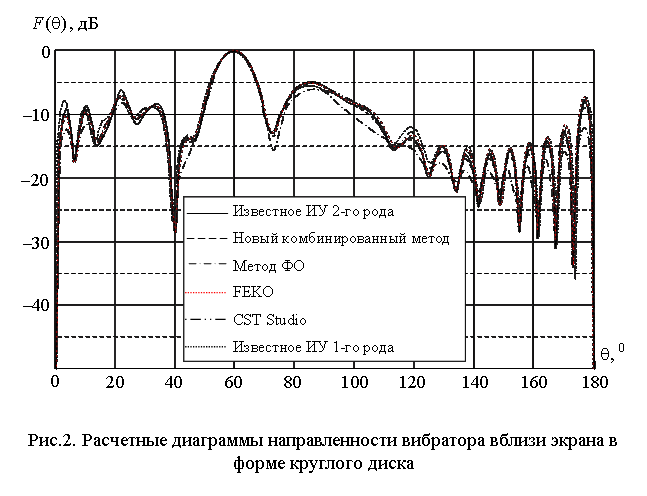
На рис.2 представлены соответствующие диаграммы направленности. Как видно из представленных данных, комбинированный метод, занимающий промежуточное положение между методами интегрального уравнения и физической оптики, дает промежуточное решение, которое, тем не менее, достаточно близко к решению, получаемому известным методом интегрального уравнения. Также видно, что полученные решения близки к решениям, получаемым с помощью специализированных программных комплексов.
В качестве второго примера рассмотрим аналогичную задачу со следующими геометрическими параметрами: - радиус диска – 10 l; - толщина диска –0,01 l; - линейный размер сегмента разбиения в разработанном комбинированном методе – 0,115 l; - линейный размер сегмента разбиения в известном методе на основе обычного интегрального уравнения второго рода – 0,1 l; - расстояние до вибратора – 5 l; - длина вибратора – 0,1 l; - ширина полосы у кромки экрана, отведенной в область интегрального уравнения в рамках комбинированных методов – 1 l; - радиус круговой площадки в центре экрана, отведенной в область интегрального уравнения в рамках комбинированных методов – 1 l.
Решение данной задачи выполнялось разработанным комбинированным методом на основе интегрального уравнения, учитывающего физико-оптическое решение, а также с помощью известного интегрального уравнения второго рода, метода физической оптики, комбинированного метода на основе интегрального уравнения первого рода, специализированного программного пакета FEKO Suite 5.4. На рис.3 представлены соответствующие диаграммы направленности. Из представленных данных можно сделать выводы, аналогичные вышеизложенным.
В качестве еще одного примера рассмотрим задачу о возбуждении квадратного экрана наклонным полуволновым вибратором. Геометрические параметры задачи следующие: - сторона экрана – 4 l; - толщина экрана – 0,05 l; - линейный размер сегмента разбиения в разработанном комбинированном методе – 0,14 l; - расстояние до центра вибратора – 1,16 l; - угол наклона вибратора к плоскости экрана – 36,9º; - ширина полосы у кромки экрана, отведенной в область интегрального уравнения в рамках комбинированных методов – 1 l; - ширина площадки в центре экрана, отведенной в область интегрального уравнения в рамках комбинированных методов – 0,3 l. Далее приводятся результаты расчета данной модели с помощью разработанного алгоритма.
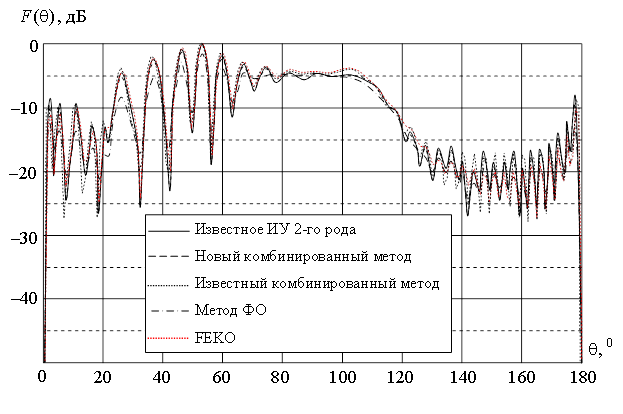
Рис.3. Расчетные диаграммы направленности вибратора вблизи экрана в форме круглого диска
На рис.4, а) показано распределение тока в данной системе. На рис.4, б) – г) представлены диаграммы направленности по θ-поляризации, по j-поляризации, а также суммарная, соответственно. Видно, что полученные результаты соответствуют теории антенн.
Проведенные численные исследования позволили оценить выигрыш в вычислительных затратах разработанного алгоритма по сравнению с известными методами. Вполне очевидно, что наибольшие затраты требуются для анализа протяженных поверхностных рассеивателей. Поэтому далее рассмотрим получающийся выигрыш на примере задачи об осесимметричном возбуждении круглого диска. Расчеты для данной задачи проводились на компьютере с процессором Intel Cove i7 с тактовой частотой 2,8 ГГц с учетом зеркальной симметрии 4-го порядка. В качестве примера в таблице 1 представлены вычислительные параметры задачи из числа решенных в ходе исследований.
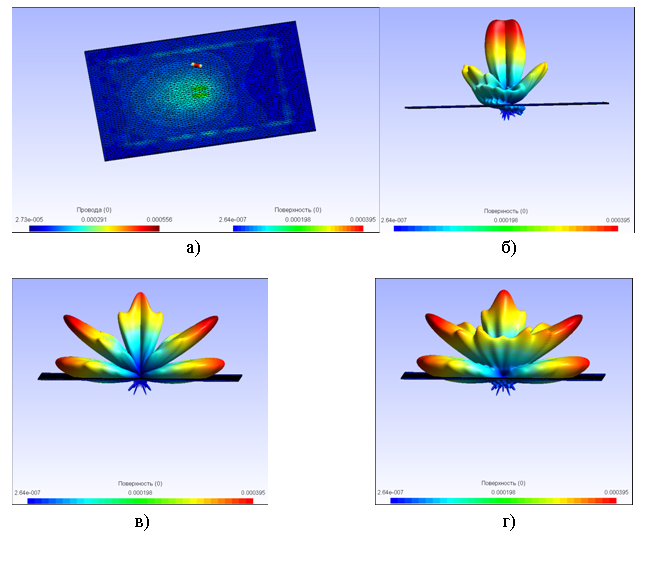
Рис.4. Результаты расчета
Таблица 1.
|
Параметр |
ИУ первого рода |
ИУ первого рода в комбинации с ФО |
Разработанный алгоритм |
|
Радиус рассеивателя |
20l |
20l |
20l |
|
Толщина рассеивателя |
– |
– |
0,05l |
|
Ширина полосы области ИУ |
– |
2l |
2l |
|
Число неизвестных в методе ИУ |
107192 |
25164 |
16105 |
|
Число неизвестных в методе ФО |
– |
107192 |
107192 |
|
Процент ненулевых элементов матрицы СЛАУ, % |
100 |
100 |
0,4 |
|
Требуемая оперативная память, МБ |
92200 |
3242 |
176 |
|
Время расчета матрицы СЛАУ, с |
16789 |
920 |
368 |
|
Время решения СЛАУ, с |
108769 |
1400 |
522 |
Как видно из представленной таблицы, разработанный алгоритм обеспечивает существенный выигрыш в вычислительных ресурсах по сравнению с другими методами при одинаковой точности по сравнению с комбинированным методом на основе интегрального уравнения первого рода.
Экспериментальное тестирование разработанного алгоритма
С целью дополнительной проверки работоспособности разработанного алгоритма были проведены соответствующие экспериментальные исследования. При этом выполнялись измерения напряженности электромагнитного поля вблизи тонких металлических рассеивателей круглой и прямоугольной формы, возбуждаемых электрически короткими вибраторами, расположенными параллельно или перпендикулярно плоскости рассеивателей. Экспериментальные исследования проводились в безэховой камере Филиала ФГУП НИИР - СОНИИР. Ниже приводятся некоторые результаты исследований.
На рис.5, 6 представлены графики измерения поля для прямоугольного рассеивателя с размерами 1450 × 1500 мм при его возбуждении коротким параллельным вибратором, расположенным на расстоянии 160 мм. Измерения проводились на частоте 4 ГГц. На рис.5 представлены результаты для контура, параллельного рассеивателю, на расстоянии 160 мм от него. На рис.6 представлены результаты для дугового контура на расстоянии 3070 мм. Каждая из кривых нормирована к своему максимуму. Для сравнения на рисунках кроме экспериментальных данных показаны расчетные кривые. Хорошее совпадение указанных значений свидетельствует о достоверности получаемых результатов.
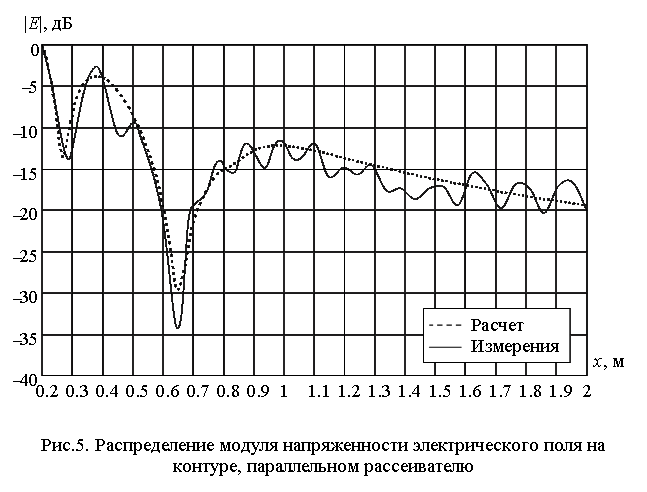
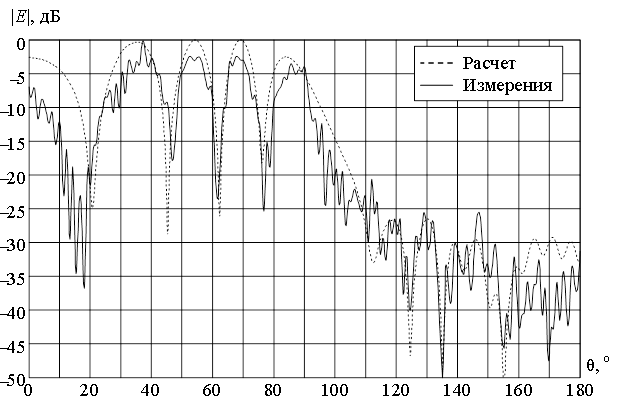
Рис.6. Распределение модуля напряженности электрического поля на дуговом контуре
Заключение
В данной работе представлены комбинированные методы электродинамического анализа, основанные на объединении методов интегральных уравнений и физико-оптических моделей. Разработанные методы позволяют анализировать произвольные антенные системы, состоящие из разнотипных антенн и располагающиеся в ограниченных условиях пространства. Разработанный на основе рассмотренных методов общий алгоритм анализа позволяет рационально сочетать достоинства комбинируемых методов и обеспечить максимально высокую эффективность и точность расчетов для эклектичных антенных систем.
Литература
1. Бузова М.А. Вопросы математического моделирования эклектичных антенных систем // V Всероссийская конференция «Радиолокация и радиосвязь» (Москва, 21 – 25 ноября 2011 г.). – М.: ООО «Информпресс-94», 2011. – С. 44 – 47.
2. Бузова М.А. Электродинамический анализ эклектичных антенных систем // Радиотехника. – 2011. – № 11. – С. 55 – 59.
3. Buzova M.A. Method of electrodynamical analysis of complex antennas systems // VIII International Conference on Antenna Theory and Techniques (September 20-23, 2011, Kyiv, Ukraine). – P. 285 – 287.
4. Jakobus U., Landstorfer F.M. Improved PO-MM hybrid formulation for scattering from three-dimensional perfectly conducting bodies of arbitrary shape // IEEE Trans. on Ant. and Prop. – 1995. – V. 43. – № 2. – P. 162 – 169.
5. Васильев Е.Н. Возбуждение тел вращения. – М.: Радио и связь, 1987. – 272 с.