УДК 621.396 : 681.2
Операция сложения распределений сигналов в пространстве идентификационных чисел
В. Ю. Кобенко
Омский государственный технический университет
Получена 21 апреля 2012 г.
Аннотация. Представлено описание, технология выполнения и формализация операции сложения двух распределений случайных величин в пространстве идентификационных чисел. Под идентификационными понимаются числа порядковой шкалы, количественно характеризующие форму сигналов.
Ключевые слова: идентификационное сложение, идентификационная алгебра распределений, идентификационные измерения, случайный сигнал, порядковая шкала.
Abstract. The description, technology of performance and formalization of addition operation of two distributions of random variables in space of identification numbers is presented. The identification numbers are understood as the numbers of a order scale quantitatively characterizing the signals form.
Keywords: identification addition, identification algebra of distributions, identification measurements, random signal, order scale.
Введение
При решении задач, связанных с обработкой и анализом сигналов часто возникает проблема формального описания взаимодействия этих сигналов, например, в результате сложения. Особенно актуальна данная проблема, если модели взаимодействующих сигналов не известны (например, когда сигналы носят случайный характер) [1]. В таком случае возникает вопрос – как аналитическим путем, описать результат взаимодействия сигналов, имеющих минимальное количество известных параметров? В настоящей работе сделана попытка решить данный вопрос в части операции сложения двух распределений случайных сигналов.
В работе [2] рассмотрены основные понятия и определения идентификационных измерений сигналов. Под идентификационными измерениями понимаются такие измерения, которые позволяют количественно оценивать форму сигналов. Основным инструментом идентификационных измерений являются порядковые идентификационные шкалы. Результат идентификационных измерений – идентификационные числа, удовлетворяющие требованиям масштабной инвариантности, эквивалентности и согласованной упорядоченности [3]. Таким образом, технология идентификационных измерений позволяет представлять сигналы любой формы (в том числе случайные) в системе порядковых измерительных шкал в виде идентификационных чисел (идентификационных параметров).
Методика исследований
Пусть даны реализации двух сигналов X(t) и Y(t) в виде распределения мгновенных значений (рис. 1) одинакового объема N. Известны энергетические характеристики сигналов в виде значений их дисперсий Dx и Dy. Известны значения идентификационных параметров сигналов NFx и NFy, найденных в соответствии с алгоритмом, описанным в [4, 5].
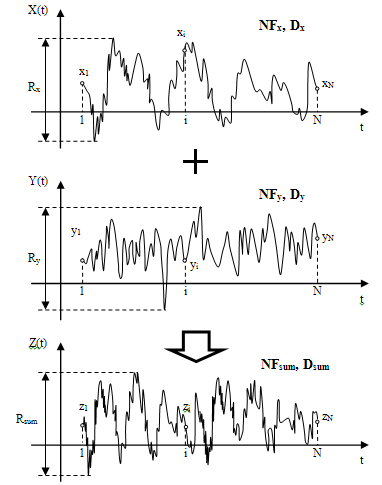
Рис. 1. Технология сложения реализаций двух сигналов X(t) и Y(t) объема N во временной области. Z(t) – результат сложения.
Задача состоит в том, чтобы, не проводя ни каких экспериментов над исходными реализациями X(t) и Y(t), идентифицировать суммарный сигнал по шкале NF, т.е. найти отображение аддитивной суммы Z(t) = X(t) + Y(t) в пространстве NF аналитически по формуле:
NFsum = f(NFx, NFy, Dx, Dy). (1)
Определение математической модели и ее коэффициентов дает возможность формально описать операцию сложения двух распределений сигналов в пространстве идентификационного параметра NF.
Параметр NF согласно [4, 5] вычисляется по формуле:
,
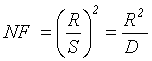(2)
где R – размах сигнала, S – среднеквадратическое отклонение, D – дисперсия.
Следовательно, NF суммарного сигнала находится по формуле:
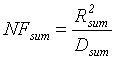, (3)
где Rsum – размах суммарного сигнала, Dsum – дисперсия суммарного сигнала (см. рис. 1). Для аналитического вычисления NFsum, необходимо вычислить Rsum = f(NFx, NFy, Dx, Dy) и Dsum = f(Dx, Dy). Дисперсия суммы двух независимых случайных величин (согласно свойств дисперсии [6]) находится по формуле:
Dsum = Dx + Dy. (4)
По формуле (2) вычисляются значения размахов исходных сигналов Rx и Ry (см. рис. 1). Размах суммарного сигнала находится по формуле:
Rsum = f (NFx, NFy, Rx, Ry). (5)
Для дальнейшего изложения введем следующие обозначения:
Rmax = max {Rx, Ry} – наибольший из размахов исходных сигналов;
Rmin = min {Rx, Ry} – наименьший из размахов исходных сигналов;
NFmax – параметр NF того сигнала, который имеет наибольший размах;
NFmin – параметр NF того сигнала, который имеет наименьший размах.
Методика проведения исследований, в основном, заключается в определении модели (5) и ее коэффициентов.
1) Реализации суммируемых сигналов X(t) и Y(t) получаются с помощью генератора случайных стационарных сигналов с заданным законом распределения [7].
2) Определяются значения размахов Rx и Ry, идентификационных параметров NFx и NFy и дисперсий Dx и Dy.
3) Чтобы исключить повторения данных при исследовании, примем за наибольший размах Rx, за наименьший – Ry, т.е. Rmax = Rx, Rmin = Ry, при этом NFmax = NFx, NFmin = NFy. Значение Ry задается в диапазоне от 0 до Rmax и реализация сигнала Y(t) при этом трансформируется.
4) Формируется реализация суммарного сигнала Z(t) = X(t) + Y(t). На рис.1 показан алгоритм нахождения мгновенных значений zi = xi + yi, 1≤i≤N.
5) Находится значение размаха Rsum суммарного сигнала Z(t) для выбранного значения Rmin.
6) После многократного повторения п.п.1 – 5 при различных значениях Rmax и Rmin для разных пар сигналов получаются зависимости, для описания которых подбирается общая математическая модель:
Rsum = f(Rmax, Rmin, К), (6)
где К – коэффициент модели, зависящий от NFmax и NFmin.
7) Коэффициент К математической модели (6) определяется следующим образом:
а) закон распределения одного из сигналов фиксируется, например Х(t);
б) находятся суммы X(t) с другими Y(t), законы распределения которых, меняются;
в) подбираются значения коэффициента К для каждой пары распределений при фиксированном Rmax и изменяющимся Rmin от 0 до Rmax:
K (NFmax)= f(NFmin, A, B, C), (7)
где A, B, C – коэффициенты модели, зависящие от NFmax;
г) для каждого коэффициента A, B, C находится математическая модель, как функция от NFmax.
8) Таким образом, общая формула для вычисления Rsum будет иметь вид:
Rsum= f(Rmax, Rmin, NFmin, A(NFmax), B(NFmax), C(NFmax)). (8)
9) Подставив выражения (8) и (4) в формулу (3), получится общая формула для вычисления NFsum:
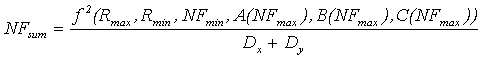. (9)
Результаты исследований
Для проведения исследований операции сложения распределений был разработан программный продукт «Система статистического анализа идентификационной суммы сигналов в пространстве NF» [8].
Для большей достоверности и статистической устойчивости результатов исследований в качестве тестовых сигналов были взяты случайные стационарные сигналы с симметричными законами распределения: двумодальный (2МОД), арксинусный (АРКС), равномерный (РАВН), треугольный (СИМП), нормальный (НОРМ), Лапласа (ЛАПЛ) и Коши (КОШИ). Перечисленные законы распределения максимально заполняют весь диапазон изменения идентификационного параметра NF [4, 5]. Объем каждой реализации N = 10000, количество усреднений результатов суммирования при одинаковых начальных условиях – 2000.
Чтобы определить математическую модель (6), просуммируем несколько реализаций сигналов в различном сочетании и представим результат на одном графике. На рис. 2 показаны характерные экспериментальные зависимости Rsum = f(Rmin) для различных сочетаний законов распределения при фиксированном значении Rmax = 1 и 0 < Rmin ≤ Rmax. В первом приближении экспериментальные данные могут быть аппроксимированы линейной зависимостью вида:
Rsum = Rmax + К • Rmin , (10)
где К – коэффициент модели (см. рис. 2), зависящий от вида закона распределения суммируемых сигналов, следовательно, зависящий от NFx и NFy.
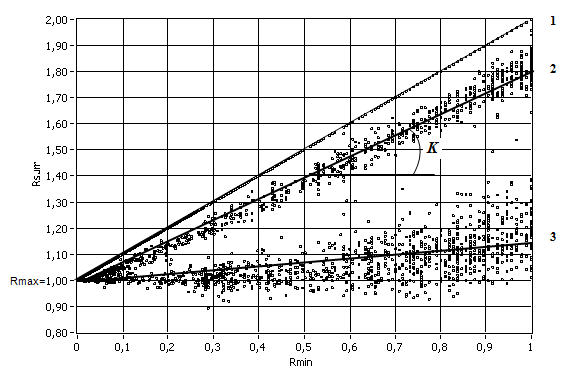
Рис. 2. Экспериментальные зависимости, полученные в результате суммирования 2МОД и 2МОД (1), СИМП и РАВН (2), ЛАПЛ и НОРМ (3) распределений (показаны аппроксимирующие прямые).
В табл. 1 представлены значения коэффициента К модели (10) для сумм различных распределений сигналов при Rmax = 1 и 0 < Rmin ≤ Rmax. Для каждой строки коэффициентов К табл. 1 определим приемлемую математическую модель, описывающую зависимость К = f(NFmin) для фиксированного NFmax, и выберем общую. В первом приближении можно остановиться на модели вида:
(11)
где A, B, C – коэффициенты модели, зависящие от NFmax (представлены в табл.2).
Таблица 1
Коэффициент К модели (10)
|
Y(t) X(t) |
Закон распределения (NFmin) |
|||||||
|
2МОД (4) |
АРКС (8) |
РАВН (12) |
СИМП (23,4) |
НОРМ (53,3) |
ЛАПЛ (167) |
КОШИ (10000) |
||
|
Закон распределения (NFmax) |
2МОД (4) |
1 |
1 |
0,998 |
0,995 |
0,960 |
0,921 |
0,690 |
|
АРКС (8) |
1 |
0,999 |
0,993 |
0,959 |
0,861 |
0,780 |
0,486 |
|
|
РАВН (12) |
0,999 |
0,993 |
0,976 |
0,918 |
0,781 |
0,689 |
0,396 |
|
|
СИМП (23,4) |
0,995 |
0,959 |
0,918 |
0,824 |
0,657 |
0,533 |
0,315 |
|
|
НОРМ (53,3) |
0,960 |
0,864 |
0,786 |
0,651 |
0,456 |
0,327 |
0,279 |
|
|
ЛАПЛ (167) |
0,922 |
0,778 |
0,691 |
0,535 |
0,324 |
0,197 |
0,261 |
|
|
КОШИ (10000) |
0691 |
0,488 |
0,396 |
0,316 |
0,278 |
0,263 |
0,145 |
|
Таблица 2
Коэффициенты модели (11)
|
Закон распределения (NFmax) |
Коэффициенты |
||
|
A |
B |
C |
|
|
2МОД (4) |
0,70 |
0,33 |
0,0047 |
|
АРКС (8) |
0,51 |
0,53 |
0,0068 |
|
РАВН (12) |
0,40 |
0,64 |
0,0089 |
|
СИМП (23,4) |
0,31 |
0,73 |
0,0147 |
|
НОРМ (53,3) |
0,23 |
0,81 |
0,0277 |
|
ЛАПЛ (167) |
0,21 |
0,90 |
0,0613 |
|
КОШИ (10000) |
0,15 |
0,91 |
0,0905 |
Для каждого коэффициента A, B, C находится математическая модель, описывающая его изменение в зависимости от NFmax. В первом приближении были выбраны модели с минимальными среднеквадратическими отклонениями:
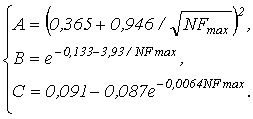(12)
Таким образом, выполнив необходимые подстановки в выражение (9), можно вычислить NFsum по формуле:
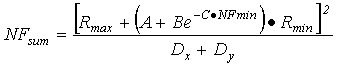, (13)
где A, B, C – коэффициенты, определяемые по формуле (12).
Итак, технология выполнения операции сложения распределений сигналов (с известными параметрами NFx, NFy, Dx и Dy) в NF-пространстве идентификационных чисел заключается в следующем:
1) вычисляются размахи Rx и Ry суммируемых сигналов исходя из формулы (2);
2) определяются наибольший Rmax и наименьший Rmin размахи:
Rmax = max {Rx, Ry};
Rmin = min {Rx, Ry};
3) определяются идентификационные параметры NFmax и NFmin:
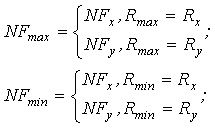
4) вычисляется идентификационный параметр NFsum суммарного сигнала по формуле (13).
Метрологические характеристики операции сложения распределений сигналов
Чтобы проверить правильность выполнения операции сложения двух распределений сигналов X(t) и Y(t) в пространстве параметра NF, найдем погрешность вычисления NFsum, при этом за истинное значение примем значение параметра NF, найденное для суммарной реализации Z(t) (см. рис.1). Определим систематическую δс и случайную δсл относительную погрешность ее среднеквадратическое отклонение (СКО) σ в соответствии с [9]. Объем каждой реализации N = 10000, количество усреднений результатов суммирования – 1000, диапазон изменения отношения размахов от 0,001 до 1000. В табл. 3 представлены данные о распределении относительной погрешности выполнения операции сложения распределений для 2МОД, АРКС, РАВН, СИМП, НОРМ, ЛАПЛ и КОШИ распределений с доверительной вероятностью 0,95 (ячейки с повторяющимися данными затушированы).
Таблица 3
Систематическая (δс) и случайная (δсл) относительные погрешности выполнения операции сложения распределений с доверительным
интервалом 2σ (доверительная вероятность 0,95)
|
|
КОШИ |
ЛАПЛ |
НОРМ |
СИМП |
РАВН |
АРКС |
2МОД |
|
|
2МОД |
δс, % |
20,1 |
-3,4 |
3,3 |
0,61 |
0,05 |
0,04 |
0,03 |
|
δсл, % |
1,69 |
0,24 |
0,19 |
0,03 |
0,03 |
0,03 |
0,02 |
|
|
2σ, % |
107 |
15,4 |
11,7 |
2,1 |
1,53 |
1,69 |
1,55 |
|
|
АРКС |
δс, % |
23,0 |
4,1 |
5,8 |
1,02 |
0,02 |
-0,16 |
|
|
δсл, % |
1,39 |
0,43 |
0,24 |
0,07 |
0,03 |
0,03 |
|
|
|
2σ, % |
87 |
27 |
15,3 |
4,1 |
1,86 |
1,52 |
|
|
|
РАВН |
δс, % |
16,4 |
3,7 |
6,9 |
2,7 |
0,41 |
|
|
|
δсл, % |
1,18 |
0,43 |
0,27 |
0,09 |
0,04 |
|
|
|
|
2σ, % |
74 |
27 |
17,1 |
5,8 |
2,4 |
|
|
|
|
СИМП |
δс, % |
-1,37 |
4,5 |
7,4 |
4,6 |
|
|
|
|
δсл, % |
0,89 |
0,44 |
0,26 |
0,16 |
|
|
|
|
|
2σ, % |
56 |
27 |
16,3 |
10,0 |
|
|
|
|
|
НОРМ |
δс, % |
0,27 |
1,02 |
0,15 |
|
|
|
|
|
δсл, % |
0,77 |
0,38 |
0,31 |
|
|
|
|
|
|
2σ, % |
48 |
24 |
19,8 |
|
|
|
|
|
|
ЛАПЛ |
δс, % |
-4,1 |
4,8 |
|
|
|
|
|
|
δсл, % |
0,62 |
0,41 |
|
|
|
|
|
|
|
2σ, % |
39 |
25 |
|
|
|
|
|
|
|
КОШИ |
δс, % |
-3,6 |
|
|
|
|
|
|
|
δсл, % |
0,56 |
|
|
|
|
|
|
|
|
2σ, % |
36 |
|
|
|
|
|
|
|
В табл. 3 жирной линией обведена область, в которой систематическая относительная погрешность не превосходит 8% с шириной доверительного интервала 2σ не более 20% при доверительной вероятности 0,95.
Выводы
Проведенные исследования позволяют сделать следующие выводы.
1) Определена операция сложения распределений случайных сигналов в пространстве идентификационного параметра NF. Формально данную операцию можно записать в виде:
,
где символом (+) обозначена операция сложения.
2) Систематическая относительная погрешность выполнения операции сложения распределений в пространстве идентификационного параметра NF не превосходит 8% при ширине доверительного интервала 2σ менее 30%, (кроме распределения КОШИ). Для ограниченных распределений 2МОД, АРКС, РАВН, СИМП систематическая относительная погрешность составляет менее 5% при ширине доверительного интервала 2σ менее 10%, (см. табл. 3).
3) Случайная относительная погрешность выполнения операции идентификационного сложения не превосходит 0,5% (для КОШИ – не более 2%) при количестве усреднений 1000.
Исследования проведены в рамках выполнения государственных заданий Министерства образования и науки Российской Федерации высшим учебным заведениям на 2012 и на плановый период 2013 и 2014 годов в части проведения научно-исследовательских работ по теме № 7.3785.2011 «Разработка теоретических основ и прикладных аспектов идентификационной алгебры сигналов».
Литература
1. Левин Б.Р. Теоретические основы статистической радиотехники. - М.: Сов. радио, 1974. - Т. I. - 552 с; 1975. - Т. 2. -392 с; 1976. - Т. 3. - 288 с.
2. Кликушин, Ю. Н. Основы идентификационных измерений / Ю. Н. Кликушин, В. Ю. Кобенко // Журнал Радиоэлектроники / М. : Изд-во ИРЭ РАН. – 2006. – № 5. – Режим доступа: http://jre.cplire.ru.
3. Гуменюк, А. С. Алгоритмы анализа структуры сигналов и данных: монография / А.С. Гуменюк, Ю.Н. Кликушин, В.Ю. Кобенко, В.Н. Цыганенко. – Омск : Изд-во ОмГТУ, 2010. – 272 с.
4. Кликушин, Ю. Н. Классификационные шкалы для распределений вероятности / Ю. Н. Кликушин // Журнал Радиоэлектроники / М. : Изд-во ИРЭ РАН. – 2000. – № 11. – Режим доступа: http://jre.cplire.ru
5. Кликушин, Ю. Н. Фрактальная шкала для измерения распределений вероятности / Ю. Н. Кликушин // Журнал Радиоэлектроники / М. : Изд-во ИРЭ РАН. – 2000. – № 3. – Режим доступа: http://jre.cplire.ru.
6. Корн, Г. Справочник по математике для научных работников и инженеров / Г. Корн, Т. Корн. – М.: Наука, 1984. – 832 с.
7. Генератор случайных сигналов с заданным законом распределения / Ю. Н. Кликушин, В. Ю. Кобенко. – М. : ИНИМ РАО ОФЭРНиО, св-во № 17515 от 25.10.2011, ВНТИЦ № 50201151369.
8. Система статистического анализа идентификационной суммы сигналов в пространстве NF / Ю. Н. Кликушин, В. Ю. Кобенко. – М. : ИНИМ РАО ОФЭРНиО, св-во № 17722 от 22.12.2011, ВНТИЦ № 50201151578.
9. Новицкий, П. В. Оценка погрешностей результатов измерения / П. В. Новицкий, И. А. Зограф. – Л. : Энергоатомиздат, 1985. – 248 с.