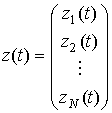алгоритм обработки сигналов в антенной решетке

 

Э. В. Амнинов ¹, Д. А. Хомяков ², Р. Н. Акиншин ³

¹ Московский институт радиоэлектроники и автоматики

² Московский государственный технический университет им. Н.Э. Баумана

³ Секции прикладных проблем при Президиуме РАН

⁴ ОАО Центральное конструкторское бюро аппаратостроения

Получена 21 апреля 2013 г.

Аннотация. Исследована модель системы пространственно-поляризационной селекции, в которой в качестве антенных элементов используются ортогональные вибраторы. Рассмотрено влияние изменений поляризационных параметров помех на ее параметры.

Ключевые слова: антенная решетка, радиолокационные сигналы, адаптивный процессор, корреляционная матрица мешающих отражений.

Abstract. A space-polarization discrimination system model was analyzed in which an orthogonal vibrator is used as antenna elements. The influence of changing of interference polarization parameters on its parameters was considered.

Keywords: antenna array, radar signals, adaptive processor, radar clutter correlation matrix, polarization basis.

 

Известно, что адаптивная обработка массивов данных антенной решеткой открывает новые возможности в подавлении мешающих отражений и позволяет осуществить гибкий сценарий сканирования диаграммы направленности антенны [1, 2]. Дополнительные возможности достигаются использованием поляриметрической информации о цели, поскольку обычная обработка массивов данных антенной решеткой не пригодна в ситуациях, когда направления цели и мешающих отражений совпадают. Одно из преимуществ поляриметрической обработки заключается в том, что цель может быть обнаружена даже в сложной помеховой обстановке за счет разницы поляриметрических свойств мешающих отражений и цели.

Проведенные к настоящему моменту исследования возможности повышения качества обработки радиолокационных сигналов за счет применения поляриметрических методов [2] свидетельствуют, что в значительной степени сложность решения этой задачи обусловлена отсутствием необходимого методического аппарата для теоретических исследований и большими потребными затратами при применении экспериментальных методов.

Поэтому целью работы является разработка алгоритма подавления мешающих отражений адаптивным процессором антенной решетки с возможностью поляриметрической обработки принимаемых сигналов.

Пусть имеется эквидистантная линейная антенная решетка с N элементами, причем во избежание дифракционных максимумов решетки, расстояние d между смежными парами диполей ≤ l/2, где l – длина волны. Полагая, что x_n(t) и y_n(t) являются соответственно, ортогональными временными реализациями сигнала n-ого диполя, векторный выходной сигнал будет иметь вид:

                                                                                       (1)

Запись n выходных векторов в вектор-столбец с 2N элементами

                                                                                          (2)

определяет временную выборку антенной решетки [1]. Полная корреляционная матрица z(t) имеет вид:

                                                                                   (3)

где E{.} обозначает математические ожидания, а ^T – знак транспонирования. Оценка максимального подобия для R рассчитывается по формуле:

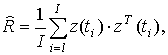                                                                               (4)

 

с использованием I имеющихся измеренных временных выборок.

Удобным является представление, полученное делением R на субматрицы формата 2×2, имеющее вид:

                                                                   (5)

В соотношении (5) элементы R_nm физически определяют корреляцию между n и m кроссовыми элементами диполя c учетом разностей фаз.

Обычно, поляризованные электромагнитные волн описываются комплексным вектором амплитуды , где α_x и α_y – векторы (амплитуды и фазы) ортогональных компонентов электрического поля. Временной сигнал в n-ом диполе, принимающем детерминированный сигнал c частотой ω и начальной фазой , может быть записан как:

                                                               (6)

где

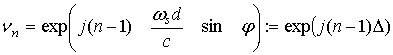                                 (7)

описывает относительную разность фаз между n-ым элементом антенны и первым элементом; φ – угол падения сигнала в плоскости xz; с – скорость света. Используя эти определения, запишем корреляционную матрицу на выходе элемента x_n и y_m:

                                           (8)

Для случая групповой цели, сигнал от которой представляет сумму K детерминированных сигналов, выражение для R_nm будет иметь вид:

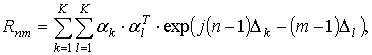                                      (9)

где индексы k и l соответствуют разным элементам групповой цели. Комбинация этих субматриц в соответствии с (5) дает корреляционную матрицу R для всей линейной антенной решетки.

Субматрица, соответствующая (8), представляет корреляционную матрицу применительно к ситуации наблюдения одной цели. В случае определения управляющего вектора в виде

                                                                 (10)

корреляционная матрица может быть записана в форме:

                                                                                   (11)

где  означает символ Кронекера.

Очевидно, что кроме сигнала в измеренных данных всегда присутствует шум. Предполагая, что он некоррелирован от элемента к элементу, имеет гауссово распределение с нулевым математическим ожиданием и равную мощность шума во всех 2N выходных сигналах, влияние на корреляционную матрицу (11) нетрудно учесть с помощью дополнительного члена θ²I_2N, где I_2N обозначает матрицу размера 2N.

Таким образом, корреляционная матрица суммы сигнала и шума будет иметь вид:

                                                                     (12)

где s² – дисперсия шума.

Важным шагом обработки является разделение сигналов в ортогональных поляриметрических каналах. Указанное достигается путем диагонализации субматриц  в , с использованием разложения собственного значения. Для любой субматрицы справедливо соотношение [3, 4]:

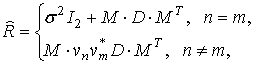                                                           (13)

где D – диагональная матрица собственных значений

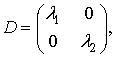                                                                                       (14)

а столбцы М – соответствующие собственные векторы. Диагонализация всех субматриц приводит к выражению:

                                   (15)

После достаточно сложных математических преобразований обратная корреляционная матрица может быть представлена в виде:

                             (16)

Здесь

                                                                               (17)

I_N означает квадратичную нулевую матрицу размера N; перестановочная матрица P имеет вид:

                                                                               (18)

 Собственные значения λ_1,2 и мощность шума σ² неизвестны и могут быть получены из измеренной корреляционной матрицы . Так, диагонализированная  может быть представлена в виде:

                                            (19)

 Поскольку собственные значения λ_1,2 всегда являются положительными, реальными числами, а |v_n,m| = 1, то исключая из (19) λ₁ или λ₂, нетрудно определить σ². Полученные таким образом значения λ_1,2 и σ² должны рассматриваться как оценки, что обусловлено ограниченным числом выборок, по которым рассчитывалась корреляционная матрица.

Для повышения точности оценок λ_1,2 целесообразно использовать усредненные матрицы, причем арифметическое усреднение возможно для всех  с идентичными членами .

Обращение корреляционной матрицы мешающих отражений может быть использовано для установки весовых коэффициентов при обработке сигнала адаптивной антенной решеткой. В поляриметрической антенной решетке для каждого ее элемента n требуются весовые значения w_xn, w_yn для ортогональных сигналов. Выходной сигнал процессора имеет вид:

                                                                                       (20)

где z – вектор сигналов антенны, определенный соотношением (2), а w – сформированный вектор весовых коэффициентов, который имеет вид:

                                                                                           (21)

а вектор V_z, может быть определен как:

                                                                       (22)

Для моделирования процесса обработки мешающих отражений при определении входных данных необходима статистическая модель сигнала. Для этого должна быть сформирована временная последовательность  для обеих ортогональных поляризаций. Очевидно, что корреляционная матрица последовательности должна быть идентична матрице когерентности мешающих отражений J_c.

Указанное может быть достигнуто преобразованием двух комплексных, гауссово распределенных величин случайного процесса .

Сигналы n(t) и c(t) связаны зависимостью:

                                                                                         (23)

Здесь T нетрудно определить из соотношения

                                                                           (24)

Допустим, что сигнал мешающих отражений является стохастической частично поляризованной плоской волной с вектором поляризации P и степенью поляризации p [2]. Пусть мешающие отражения при моделировании имеют левостороннюю круговую поляризацию () с p = 0,8.

При моделировании процесса обработки использованы следующие исходные данные: линейная антенная решетка содержит 16 элементов и принимает детерминированный сигнал мощностью |a|² = 2 с направления sin φ = 0,5 и сигнал источника мешающих отражений с направления sin φ = – 0,4 мощностью  без адаптации (w = v_z). Для каждого направления φ соответствующий весовой коэффициент V_z формируется на выходе процессора по формуле (21). Число направлений выбрано равным 40.

Предварительно проведена оценка и инвертирование корреляционной матрицы мешающих отражений. Показано, что имеет место отбеливающий эффект пространственного узкополосного режекторного фильтра, за счет умножения помехи на предварительно вычисленные коэффициенты фильтра W_xn, W_yn.. В случае возникновения второй цели с того же направления, что и мешающие отражения и с той же мощностью, что и цель № 1, она будет легко обнаруживаться, благодаря своей противоположной поляризации – правосторонней, круговой (), т.е существует возможность путем изменения главных диагональных элементов корреляционной матрицы мешающих отражений осуществлять выбор между лучшим их подавлением или лучшим обнаружением цели в условиях мешающих отражений. Указанный эффект следует принимать в расчет при проектировании АР.

Таким образом, предложен эффективный алгоритм обращения корреляционной матрицы мешающих отражений, при использовании ее особой структуры в случае с одним источником отражения. Этот алгоритм может быть частью адаптивного алгоритма процессора антенной решетки. Проведенное моделирование показало эффективность поляриметрической адаптивной обработки. Аналогичные расчеты можно проделать для полностью поляриметрических РЛС.

Литература

1. Воскресенский Д.И. Антенны с обработкой сигнала. – М.: Сайнс-Пресс, 2002. – 80 с.

2. Cherardelli H., Guillii D., Fossi M., Freni A. Adaptive polarization for rejection of ground clatter // Onde elect. – 1989. – 69. – No. 6. – Pp. 5-10.

3. Wanielik G. Signaturuntersuchungen an einem polarimetrischen Pulsradar // Fortschr. – Ber. VDI Reihe 10. – Nr. 97; VDI – Verlag, Dusseldorf, 1988.

4. Монзинго П.А., Миллер Т.У. Адаптивные антенные решетки: введение в теорию. – М.: Радио и связь, 1986. – 448 с.