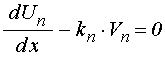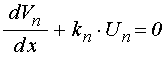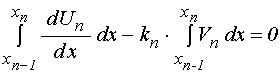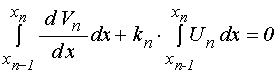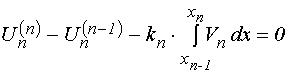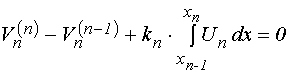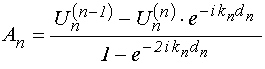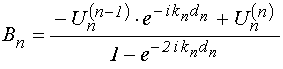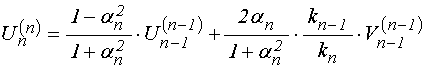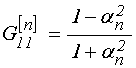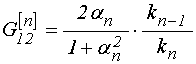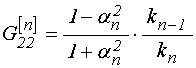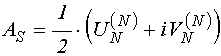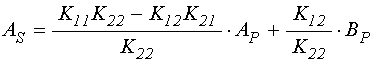УДК 537.874; 537.624
МЕТОД ИСКЛЮЧЕНИЯ ДЛЯ РАСЧЕТА РАСПРОСТРАНЕНИЯ ВОЛН ЧЕРЕЗ СРЕДЫ СО СТУПЕНЧАТЫМИ НЕОДНОРОДНОСТЯМИ
И. В. Антонец 1, Л. Н. Котов 1, В. Г. Шавров 2, В. И. Щеглов 2
1 Сыктывкарский государственный университет, Сыктывкар, Россия
2 Институт радиотехники и электроники РАН, Москва, Россия
Получена 16 апреля 2013 г.
Аннотация. Предложен метод расчета амплитуд отраженной и проходящей волн при падении двух встречных волн на многослойную структуру со ступенчатой неоднородностью, названный «методом исключения». Получены условия сопряжения, соотношения прямой передачи и рекуррентные формулы для функциональных коэффициентов, позволяющие найти амплитуды выходящих из структуры волн через амплитуды входящих для произвольного числа слоев структуры. Работа метода продемонстрирована на численном примере многослойной структуры из десяти сред. Даны рекомендации для применения метода исключения к задачам о распространении электромагнитных волн для случаев нормального и наклонного падения.
Ключевые слова: распространение волн, многослойные неоднородные структуры.
Abstract. The method of calculation reflected and penetrated waves amplitudes accompanying the two travelling in the opposite directions waves falling on the multilayer stepwise nonuniform structure is offered. This method is named as “exclusion method”. It is found the conjugate conditions, the forward transmission conversions and recurrent formulas for functional coefficients which allow to find the outgoing from the structure waves amplitudes through the incoming waves amplitudes for arbitrary quantity of layers. The method capacity for work is demonstrated on numerical example of multilayer structure consisted of ten layers. It is shown that these method can be applied to problems on propagation of electromagnetic waves in the cases of the normal and oblique incidence.
Key words: wave propagation, multilayer nonuniform structure.
Введение
Задачи о распространения волн в неоднородных средах издавна привлекают внимание исследователей [1-12]. Точное аналитическое решение волнового уравнения в такой среде возможно только для некоторых весьма специфических видов неоднородностей, некоторые из которых рассмотрены в работах [1,8,11]. Ограниченность точных методов частично преодолевается при использовании приближенного представления исследуемой среды в виде многослойной структуры, состоящей из однородных слоев. При этом решения волнового уравнения в каждом слое в отдельности сшиваются друг с другом на основе граничных условий [3-8]. Наиболее последовательным в этом случае является прямой метод [3,4,8,13-15], однако необходимость раскрытия определителей высоких порядков ограничивает его реальное применение числом слоев не более пяти. Для большего числа слоев применяются методы последовательных вычислений: матрицы [4,7,16] и импеданса [5,8,17]. Эти методы состоят в повторении большого количества однотипных вычислений, проводимых от конца структуры к ее началу, что затрудняет расчет для динамически меняющихся сред, а для встречных волн требует двукратного прохождения.
Для структур с достаточно тонкими слоями довольно эффективным является метод усреднения [3,13,14,18-22], однако уже для числа слоев больше двух идеологическая сложность метода резко возрастает, а различие вариантов сшивания решений приводят к неопределенности получающихся результатов.
В то же время, ряд задач, особенно в неоднородной динамически меняющейся среде, требует разработки более удобного экспресс-метода, позволяющего определять отражение и прохождение волн через структуру как для прямых, так и для встречных волн за один проход от начала структуры к ее концу и пригодный для слоев любой толщины без каких-либо масштабных ограничений.
Настоящая работа посвящена разработке такого метода и демонстрации возможности его применения на примере ступенчатой структуры с линейной неоднородностью.
1. Геометрия задачи и волновые уравнения для встречных волн
Рассмотрим падение двух встречных одномерных волн на многослойную структуру, состоящую из произвольного числа плоскопараллельных сред. Геометрия задачи показана на рис.1.
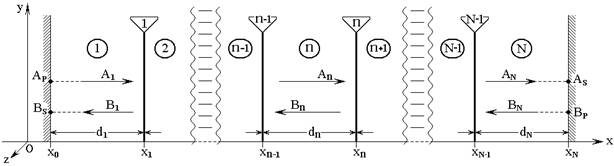
Рис.1. Геометрия распространения встречных одномерных волн.
Структура содержит ![]() сред, в виде сложенных друг с другом
плоских однородных бесконечно протяженных пластин. Среды разделены
сред, в виде сложенных друг с другом
плоских однородных бесконечно протяженных пластин. Среды разделены ![]() плоскими бесконечно тонкими границами. Декартова
система координат
плоскими бесконечно тонкими границами. Декартова
система координат ![]() выбрана таким образом, что плоскость
выбрана таким образом, что плоскость
![]() параллельна плоскостям пластин, а ось
параллельна плоскостям пластин, а ось ![]() им перпендикулярна. Координаты границ
равны
им перпендикулярна. Координаты границ
равны ![]() ,
, ![]() , …,
, …,![]() , расстояния между ними:
, расстояния между ними:
![]() .
(1)
.
(1)
Вдоль оси ![]() в
обоих ее направлениях в структуре могут распространяться плоские одномерные
волны, волновые числа которых в средах с
в
обоих ее направлениях в структуре могут распространяться плоские одномерные
волны, волновые числа которых в средах с ![]() по
по ![]() равны
равны ![]() ,
, ![]() , . . . ,
, . . . , ![]() .
.
Для решения задачи о распространении волн через многослойную структуру, будем использовать метод сшивания частных решений в отдельных слоях, который назовем «методом исключения по ячейкам», или более кратко «методом исключения».
2. Общая схема метода исключения
Для каждой среды рассматриваются две волновые функции, одна из которых является суммой встречных волн, а другая – частным от деления производной от первой на волновое число. Вся структура разбивается на ячейки, каждая из которых включает в себя одну среду и одну границу. После нахождения соотношений между упомянутыми функциями на внешних сторонах каждой ячейки, полученные соотношения сшиваются простым «прикладыванием» друг к другу, в результате чего амплитуды внутренних волн взаимно исключаются. В конечном счете получается система из двух линейных уравнений, содержащая в качестве неизвестных амплитуды выходящих из структуры волн, а в качестве параметров – амплитуды входящих.
Таким образом получаются две основных задачи: первая – нахождение в общем виде решения для одной ячейки с произвольным номером, вторая – решение системы уравнений, получаемой сшиванием решений в отдельных ячейках.
3. Решение для одной ячейки с произвольным номером
Координатная часть волнового
уравнения в среде с номером ![]() имеет вид:
имеет вид:
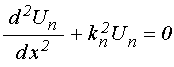 ,
(2)
,
(2)
где ![]() –
волновая функция,
–
волновая функция, ![]() – волновое число.
– волновое число.
Решение этого уравнения,
нормированное относительно точки исхода волны, имеет вид суперпозиции прямой ![]() и встречной
и встречной ![]() волн,
распространяющихся соответственно в положительном и отрицательном направлениях
оси
волн,
распространяющихся соответственно в положительном и отрицательном направлениях
оси ![]() :
:
Будем называть это решение «волновой функцией первого рода».
Для дальнейшего рассмотрения введем также функцию:
которую будем называть «волновой функцией второго рода».
Волновые функции первого и второго рода связаны соотношением:
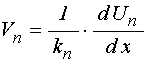 ;
(5)
;
(5)
Преобразуя (5), а также
дифференцируя (4), получаем систему уравнений для ![]() и
и ![]() :
:
4. Амплитуды волн на внешних границах структуры
В структуру входят и выходят
волны только на ее внешних поверхностях, то есть при ![]() и
и
![]() . Обозначим амплитуды входящих в структуру
встречных волн через
. Обозначим амплитуды входящих в структуру
встречных волн через ![]() и
и ![]() , а
амплитуды выходящих – через
, а
амплитуды выходящих – через ![]() и
и ![]() .
.
В среде ![]() , то
есть при
, то
есть при ![]() , функция
, функция ![]() имеет
вид:
имеет
вид:
![]() .
(8)
.
(8)
При этом в структуру при ![]() входит волна:
входит волна:
![]() .
(9)
.
(9)
Из структуры при ![]() выходит волна:
выходит волна:
![]() ;
(10)
;
(10)
В среде ![]() , то
есть при
, то
есть при ![]() , функция
, функция ![]() имеет
вид:
имеет
вид:
![]() .
(11)
.
(11)
При этом в структуру при ![]() входит волна:
входит волна:
![]() .
(12)
.
(12)
Из структуры при ![]() выходит волна:
выходит волна:
![]() .
(13)
.
(13)
Таким образом, амплитуды волн,
распространяющихся в средах ![]() и
и ![]() , имеют вид:
, имеют вид:
Замечание. Поскольку в дальнейшем рассмотрении неоднократно будут использоваться значения волновых функций на границах сред, для упрощения записи введем для обозначения граничного значения функции вместо традиционно используемой вертикальной черты с индексом границы внизу, заключенный в скобки индекс границы наверху, то есть будем писать:
![]() ,
(18)
,
(18)
где ![]() –
функция
–
функция ![]() или
или ![]() ,
, ![]() – номер среды,
– номер среды, ![]() –
номер границы.
–
номер границы.
5. Общая схема последовательного перехода
Будем рассматривать задачу для
структуры в целом путем последовательного перехода от среды ![]() до среды
до среды ![]() .
.
Распространение волны в слоистой структуре складывается из двух процессов: распространения волны между границами и ее преобразования при переходе через границу. В соответствии с этим будем рассматривать два вида условий: условия сопряжения, характеризующие изменение волны при распространении между границами и условия граничные, характеризующие изменение волны при прохождении границы.
Начнем рассмотрение с условий сопряжения. Для их получения в общем случае можно использовать прямой метод, а в случае достаточно тонких слоев – метод усреднения. Рассмотрим эти методы по отдельности.
6. Условия сопряжения. Прямой метод
Рассмотрим получение условий сопряжения прямым методом.
Интегрируем (6) и (7) по ![]() от
от ![]() до
до ![]() :
:
Выполняя интегрирование в первых слагаемых этих выражений, получаем:
Для дальнейших преобразований удобно
выразить функции ![]() и
и ![]()
через амплитуды волн ![]() и
и ![]() в
соответствии с (3)-(4):
в
соответствии с (3)-(4):
![]() ;
(23)
;
(23)
![]() ;
(24)
;
(24)
![]() ;
(25)
;
(25)
![]() .
(26)
.
(26)
Рассматривая (23)-(24) как систему
двух уравнений относительно ![]() и
и ![]() , получаем:
, получаем:
Аналогично из (25)-(26) получаем:
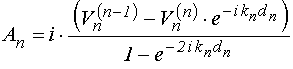 ;
(29)
;
(29)
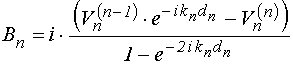 .
(30)
.
(30)
Интегралы, во вторых слагаемых выражений (19) и (20), выразим через (3)-(4):
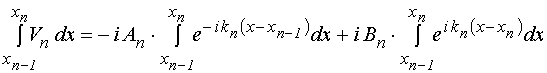 ; (31)
; (31)
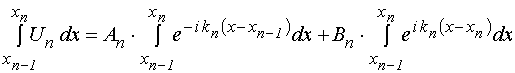 .
(32)
.
(32)
Входящие в (31)-(32) интегралы равны:
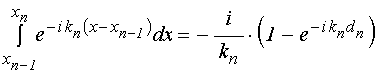 ;
(33)
;
(33)
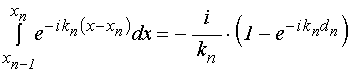 .
(34)
.
(34)
Подставляя (33)-(34) в (31)-(32), получаем:
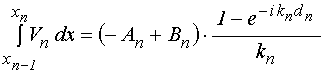 ;
(35)
;
(35)
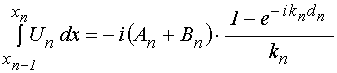 .
(36)
.
(36)
Подставляя (27)-(28) в (35) и (29)-(30) в (36), получаем входящие в (19)-(20) интегралы в виде:
 ;
(37)
;
(37)
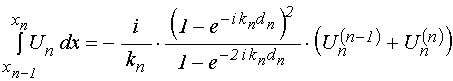 .
(38)
.
(38)
Подставляя (37)-(38) в (21)-(22) получаем:
 ;
(39)
;
(39)
 .
(40)
.
(40)
Введем обозначение:
С этим обозначением (39)-(40) принимают вид:
![]() ;
(42)
;
(42)
![]() .
(43)
.
(43)
Раскрывая скобки и меняя знаки, приведем эти выражения к более удобному для дальнейшего рассмотрения виду:
Поскольку выражения (44)-(45)
связывают (то есть как бы сопрягают между собой) значения функций ![]() и
и ![]() на
противоположных границах среды
на
противоположных границах среды ![]() при
при ![]() и
и ![]() , будем
называть их «условиями сопряжения» функций
, будем
называть их «условиями сопряжения» функций ![]() и
и ![]() для среды
для среды ![]() ,
заключенной между границами
,
заключенной между границами ![]() и
и ![]() .
.
7. Условия сопряжения. Метод усреднения
Рассмотрим получение условий сопряжения методом усреднения.
Введем усреднение в интегралах, входящих во вторые слагаемые выражений (19)-(20):
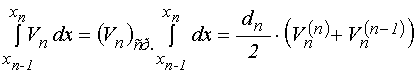 ;
(46)
;
(46)
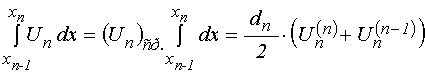 .
(47)
.
(47)
Подставляя (46)-(47) в (21)-(22), получаем:
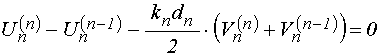 ;
(48)
;
(48)
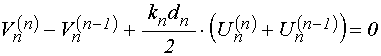 .
(49)
.
(49)
Введем обозначение:
Подставляя (50) в (48)-(49),
раскрывая скобки, умножая оба выражения на ![]() и
меняя порядок слагаемых, получаем:
и
меняя порядок слагаемых, получаем:
![]() ;
(51)
;
(51)
![]() .
(52)
.
(52)
Как видно из сравнения с
(44)-(45), полученные условия сопряжения совпадают с полученными прямым методом
с точностью до замены выражения для ![]() с (41) на (50).
с (41) на (50).
Замечание. Полученные в работе [13] выражения, аналогичные (44)-(45) и (51)-(52), названы там «граничными условиями», что не вполне корректно, так как здесь присутствует не одна граница, а две. Следует сказать, что подобная некорректность терминологии является довольно распространенной и встречается, например, в работе [20] и ряде других. По нашему мнению, термин «условия сопряжения» более адекватно отражает положение дел, то есть является более корректным, поэтому он и используется далее.
8. Граничные условия
Рассмотрим теперь второй вид условий – граничные условия.
Условия на границе с номером ![]() для волновых функций первого рода требуют
равенства самих функций и их производных, то есть:
для волновых функций первого рода требуют
равенства самих функций и их производных, то есть:
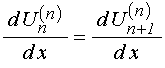 .
(54)
.
(54)
Поскольку волновая функция
второго рода пропорциональна производной от функции первого рода, то вместо
второго условия для производной от ![]() (54), можно использовать
следующее из (6) условие для функции второго рода
(54), можно использовать
следующее из (6) условие для функции второго рода ![]() :
:
Таким образом, пара условий (53) и (55) полностью определяет соотношения между амплитудами распространяющихся волн на границе.
9. Соотношения прямой передачи
Метод исключения по ячейкам
предполагает разбиение всей структуры на ячейки, каждая из которых содержит
какую-то одну среду с прилегающей к ней одной границей, с последующим сшиванием
ячеек последовательным прохождением от начала структуры к ее концу. Сшивание,
осуществляемое переходом от ячейки к ячейке в положительном направлении оси ![]() , будем называть «прямой передачей».
, будем называть «прямой передачей».
К одному участку среды с противоположных сторон примыкают две границы, поэтому в качестве единичной ячейки можно рассматривать участок среды в совокупности с той или иной границей.
Будем называть ячейкой первого
рода участок среды с границей, примыкающей к нему со стороны меньших значений
координаты ![]() , то есть участок среды с предшествующей
ему границей. В свою очередь участок среды со следующей за ним границей будем
называть ячейкой второго рода.
, то есть участок среды с предшествующей
ему границей. В свою очередь участок среды со следующей за ним границей будем
называть ячейкой второго рода.
10. Прямая передача первого рода
Рассмотрим прямую передачу
первого рода. Схема одной элементарной ячейки с номером ![]() для
этого случая показана на рис.2.
для
этого случая показана на рис.2.
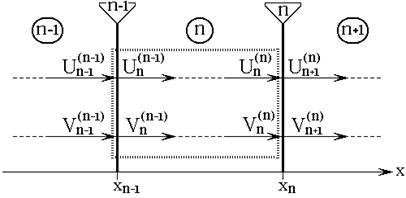
Рис.2. Схема ячейки с номером ![]() при прямой передаче первого рода.
при прямой передаче первого рода.
Ячейка включает в себя участок
среды, заключенный между границами при ![]() и
и ![]() , а также предшествующую этому участку
границу при
, а также предшествующую этому участку
границу при ![]() . На рис.2 контуры такой ячейки показаны
точечной линией.
. На рис.2 контуры такой ячейки показаны
точечной линией.
Будем условно считать, что в
ячейку «входят» функции ![]() и
и ![]() и «выходят» функции
и «выходят» функции ![]() и
и ![]() .
.
Граничные условия на границе ![]() можно записать в виде:
можно записать в виде:
Условия сопряжения для среды ![]() , заключенной между границами
, заключенной между границами ![]() и
и ![]() , имеют
вид:
, имеют
вид:
![]() ;
(58)
;
(58)
![]() .
(59)
.
(59)
Рассматривая эти условия как
систему уравнений для определения «выходящих» из ячейки функций ![]() и
и ![]() ,
получаем:
,
получаем:
 ;
(60)
;
(60)
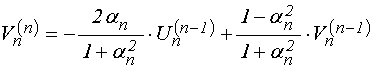 .
(61)
.
(61)
Подстановка в эти формулы следующих
из граничных условий соотношений (56)-(57), позволяет исключить функции ![]() и
и ![]() , в
результате чего получаем:
, в
результате чего получаем:
Эти формулы выражают «выходящие»
из ячейки ![]() функции
функции ![]() и
и ![]() через «входящие» в эту ячейку функции
через «входящие» в эту ячейку функции ![]() и
и ![]() . Будем
называть формулы (62)-(63) «соотношениями прямой передачи первого рода»
для среды с номером
. Будем
называть формулы (62)-(63) «соотношениями прямой передачи первого рода»
для среды с номером ![]() .
.
Запишем те же выражения в обобщенном виде, для чего введем обозначения:
В этих обозначениях соотношения
(62)-(63) для среды ![]() принимают вид:
принимают вид:
11. Прямая передача второго рода
Рассмотрим прямую передачу
второго рода. Схема одной элементарной ячейки с номером ![]() для
этого случая показана на рис.3.
для
этого случая показана на рис.3.

Рис.3. Схема ячейки с номером ![]() при прямой передаче второго рода.
при прямой передаче второго рода.
Ячейка включает в себя участок
среды, заключенный между границами при ![]() и
и ![]() , а также следующую за этим участком границу
при
, а также следующую за этим участком границу
при ![]() . На рис.3 контуры такой ячейки показаны
точечной линией.
. На рис.3 контуры такой ячейки показаны
точечной линией.
Будем условно считать, что в
ячейку «входят» функции ![]() и
и ![]() и «выходят» функции
и «выходят» функции ![]() и
и ![]() .
.
Граничные условия на границе ![]() можно записать в виде:
можно записать в виде:
![]() ;
(70)
;
(70)
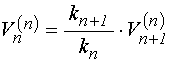 .
(71)
.
(71)
Условия сопряжения для среды ![]() , заключенной между границами
, заключенной между границами ![]() и
и ![]() , имеют
вид:
, имеют
вид:
![]() ;
(72)
;
(72)
![]() . (73)
. (73)
Рассматривая эти условия как
систему уравнений относительно ![]() и
и ![]() , а также с помощью граничных условий
(70)-(71) исключая
, а также с помощью граничных условий
(70)-(71) исключая ![]() и
и ![]() ,
получаем:
,
получаем:
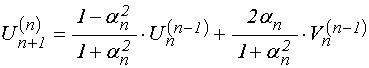 ;
(74)
;
(74)
 .
(75)
.
(75)
Эти формулы выражают «выходящие»
из ячейки ![]() функции
функции ![]() и
и ![]() через «входящие» в эту ячейку функции
через «входящие» в эту ячейку функции ![]() и
и ![]() . Будем
называть формулы (74)-(75) «соотношениями прямой передачи второго рода»
для среды с номером
. Будем
называть формулы (74)-(75) «соотношениями прямой передачи второго рода»
для среды с номером ![]() .
.
Запишем те же выражения в обобщенном виде, для чего введем обозначения:
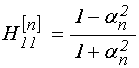 ;
(76)
;
(76)
 ;
(77)
;
(77)
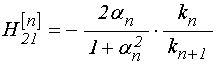 ;
(78)
;
(78)
 .
(79)
.
(79)
В этих обозначениях соотношения
(74)-(75) для среды ![]() принимают вид:
принимают вид:
![]() ;
(80)
;
(80)
![]() .
(81)
.
(81)
Замечание. Как видим, разбиение структуры на
ячейки при прямой передаче допускает два варианта. С другой стороны, при любом
варианте разбиения сшивание ячеек можно осуществить не только в положительном,
но и в отрицательном направлении оси ![]() . Подобное сшивание в
отрицательном направлении будем называть «обратной передачей». Таким образом,
метод исключения по ячейкам допускает четыре возможных варианта, все из которых
должны приводить к одному и тому же результату. Как идеологическая, так и математическая
сложности всех этих вариантов примерно одинаковы, поэтому выбор любого из них
может определяться конкретными условиями задачи или удобством ее решения. По
этой причине в дальнейшем рассмотрении для простоты ограничимся только подробным
рассмотрением прямой передачи первого рода. Все остальные случаи могут быть
рассмотрены аналогично.
. Подобное сшивание в
отрицательном направлении будем называть «обратной передачей». Таким образом,
метод исключения по ячейкам допускает четыре возможных варианта, все из которых
должны приводить к одному и тому же результату. Как идеологическая, так и математическая
сложности всех этих вариантов примерно одинаковы, поэтому выбор любого из них
может определяться конкретными условиями задачи или удобством ее решения. По
этой причине в дальнейшем рассмотрении для простоты ограничимся только подробным
рассмотрением прямой передачи первого рода. Все остальные случаи могут быть
рассмотрены аналогично.
12. Процедура последовательных подстановок
Соотношения прямой передачи для
структуры, состоящей из произвольного числа сред ![]() , могут
быть получены из соотношений прямой передачи для каждой из сред по отдельности
путем последовательных подстановок.
, могут
быть получены из соотношений прямой передачи для каждой из сред по отдельности
путем последовательных подстановок.
При этом, поскольку вне
структуры, то есть при ![]() и
и ![]() ,
волноведущих сред нет, то среды
,
волноведущих сред нет, то среды ![]() и
и ![]() находятся в особом положении и требуют отдельного
рассмотрения.
находятся в особом положении и требуют отдельного
рассмотрения.
Поскольку при прямой передаче
граница структуры при ![]() находится вне первой ячейки, то
для сохранения общности записи на этой границе введем в рассмотрение функции
находится вне первой ячейки, то
для сохранения общности записи на этой границе введем в рассмотрение функции ![]() и
и ![]() ,
значение которых определим далее.
,
значение которых определим далее.
13. Входная и выходная ячейки
На внешних поверхностях структуры
в целом, то есть при ![]() и
и ![]() волны
входят в структуру и выходят из нее, то есть вместо классических граничных
условий задаются амплитуды входящих волн и анализируются амплитуды выходящих.
Поэтому ячейки в первой и последней средах находятся в условиях, отличных от
остальных ячеек, то есть применение стандартной процедуры последовательных
подстановок допустимо только в пределах сред от
волны
входят в структуру и выходят из нее, то есть вместо классических граничных
условий задаются амплитуды входящих волн и анализируются амплитуды выходящих.
Поэтому ячейки в первой и последней средах находятся в условиях, отличных от
остальных ячеек, то есть применение стандартной процедуры последовательных
подстановок допустимо только в пределах сред от ![]() до
до ![]() , а первая и последняя среды (
, а первая и последняя среды (![]() и
и ![]() )
требуют отдельного рассмотрения.
)
требуют отдельного рассмотрения.
14. Начало структуры (среды ![]() и
и ![]() )
)
Схема распространения волн вблизи
начала структуры представлена на рис.4. Контуры ячеек при ![]() и
и ![]() показаны
точечными линиями.
показаны
точечными линиями.
Задача состоит в том, чтобы
связать волновые функции ![]() и
и ![]() с амплитудами волн:
с амплитудами волн: ![]() – входящей в структуру при координате
– входящей в структуру при координате ![]() и
и ![]() –
выходящей из структуры при том же значении координаты.
–
выходящей из структуры при том же значении координаты.

Рис.4. Схема распространения волн вблизи начала структуры.
В общем виде соотношения прямой
передачи для среды ![]() имеют вид:
имеют вид:
![]() ;
(82)
;
(82)
![]() ;
(83)
;
(83)
На границе 0 (то есть на левой внешней поверхности структуры) изменения волновых функций не происходит, поэтому граничные условия имеют вид:
![]() ;
(84)
;
(84)
![]() .
(85)
.
(85)
Волновое число при этом также не
меняется, поэтому в соотношениях (62)-(63) при ![]() можно
положить:
можно
положить:
![]() .
(86)
.
(86)
Таким образом, соотношения прямой передачи для среды 1, с учетом (64)-(67) и (84)-(85), принимают вид:
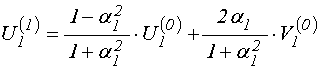 ;
(87)
;
(87)
 .
(88)
.
(88)
Определим теперь волновые функции
![]() и
и ![]() .
.
В среде 1 волновые функции имеют вид:
![]() ;
(89)
;
(89)
![]() .
(90)
.
(90)
На границе 0 при ![]() эти функции равны:
эти функции равны:
![]() ;
(91)
;
(91)
![]() .
(92)
.
(92)
Подставляя ![]() и
и
![]() в соответствии с (14)-(15), получаем:
в соответствии с (14)-(15), получаем:
![]() ;
(93)
;
(93)
![]() .
(94)
.
(94)
Подставляя (93)-(94) в (87)-(88), получаем:
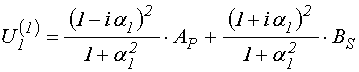 ;
(95)
;
(95)
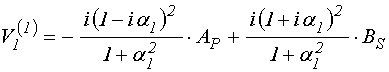 .
(96)
.
(96)
Таким образом, искомые соотношения получены.
Как видно из (95)-(96), эти соотношения можно представить в виде:
![]() ;
(97)
;
(97)
![]() ,
(98)
,
(98)
где введены обозначения:
15. Конец структуры (среды ![]() и
и ![]() )
)
Схема распространения волн вблизи
конца структуры представлена на рис.5. Контуры ячеек ![]() и
и
![]() показаны точечными линиями.
показаны точечными линиями.
Задача состоит в том, чтобы связать
амплитуды ![]() и
и ![]() с
волновыми функциями
с
волновыми функциями ![]() и
и ![]() .
.
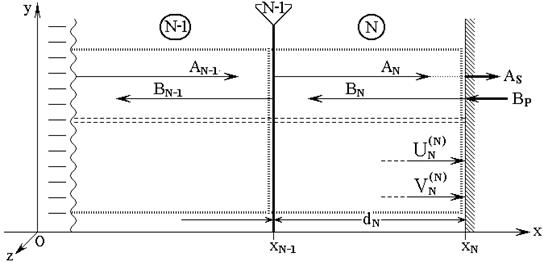
Рис.5. Схема распространения волн вблизи конца структуры.
Волновые функции в среде ![]() имеют вид:
имеют вид:
![]() ;
(101)
;
(101)
![]() .
(102)
.
(102)
На внешней поверхности структуры
при ![]() эти функции равны:
эти функции равны:
![]() ;
(103)
;
(103)
![]() .
(104)
.
(104)
Учитывая выражения для ![]() и
и ![]() в
соответствии с (16)-(17), получаем:
в
соответствии с (16)-(17), получаем:
![]() ;
(105)
;
(105)
![]() .
(106)
.
(106)
При численном решении
представляет интерес обратное соотношение, то есть выражение ![]() и
и ![]() через
через ![]() и
и ![]() .
Рассматривая (105)-(106) как систему уравнений относительно
.
Рассматривая (105)-(106) как систему уравнений относительно ![]() и
и ![]() ,
получаем:
,
получаем:
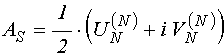 ;
(107)
;
(107)
 .
(108)
.
(108)
16. Полная процедура последовательных подстановок
Рассмотрим полную процедуру
последовательных подстановок, начиная с левой границы структуры при ![]() и кончая правой границей при
и кончая правой границей при ![]() . Во всех средах будем пользоваться
соотношениями прямой передачи.
. Во всех средах будем пользоваться
соотношениями прямой передачи.
Запишем соотношения между амплитудами на границах и во всех средах.
Левая граница структуры и среда 1:
Среда 2:
![]() ;
(111)
;
(111)
![]() .
(112)
.
(112)
- - - - - - - - - - - - - - - - - - - - - -
Среда ![]() :
:
![]() ;
(113)
;
(113)
![]() .
(114)
.
(114)
- - - - - - - - - - - - - - - - - - - - - -
Среда ![]() :
:
![]() ;
(115)
;
(115)
![]() .
(116)
.
(116)
Правая граница структуры:
Замечание. Здесь и далее
верхний индекс при ![]() означает не номер границы, а
номер среды и для отличия от подобных индексов при
означает не номер границы, а
номер среды и для отличия от подобных индексов при ![]() и
и ![]() заключен в квадратные скобки.
заключен в квадратные скобки.
При подстановке предыдущих
соотношений для ![]() и
и ![]() в
последующие, после приведения соответствующих подобных членов, при функциях
в
последующие, после приведения соответствующих подобных членов, при функциях ![]() и
и ![]() из
коэффициентов
из
коэффициентов ![]() ,
, ![]() ,
, ![]() ,
, ![]() образуются
сложные комбинации. Получающиеся в результате соотношения для сред со
образуются
сложные комбинации. Получающиеся в результате соотношения для сред со ![]() по
по ![]() , можно
записать в виде:
, можно
записать в виде:
где упомянутые комбинации обозначены
через ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Выражения (119)-(120) можно назвать «условиями сопряжения волновых функций для структуры в целом».
Можно видеть, что упомянутые
последовательные подстановки на каждом шаге сохраняют линейную зависимость
последующих величин от предыдущих. При этом и зависимость амплитуд и ![]() от
от ![]() и
и ![]() также сохранит линейность, то есть будут
выполняться соотношения:
также сохранит линейность, то есть будут
выполняться соотношения:
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() – функции параметров сред, определяемые в
процессе подстановок.
– функции параметров сред, определяемые в
процессе подстановок.
Выражения (121)-(122) можно назвать «условиями сопряжения амплитуд для структуры в целом».
Поскольку в структуру входят
волны ![]() и
и ![]() , а
выходят –
, а
выходят – ![]() и
и ![]() , то конечной
задачей является нахождение амплитуд
, то конечной
задачей является нахождение амплитуд ![]() и
и ![]() через
через ![]() и
и ![]() . Амплитуду
. Амплитуду ![]() можно
сразу найти из (122), после чего подстановка полученного значения в (121)
позволяет найти и
можно
сразу найти из (122), после чего подстановка полученного значения в (121)
позволяет найти и ![]() . В результате получаем:
. В результате получаем:
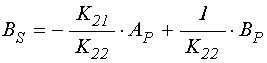 .
(124)
.
(124)
Подставляя (109)-(110) в (119)-(120), и далее полученные выражения – в (117)-(118), после чего, сравнивая с (121)-(122), находим:
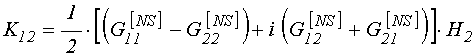 ;
(126)
;
(126)
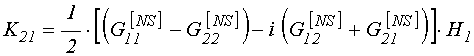 ;
(127)
;
(127)
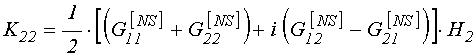 .
(128)
.
(128)
Таким образом, задача получения
амплитуд выходящих волн ![]() и
и ![]() через амплитуды входящих
через амплитуды входящих ![]() и
и ![]() в
общем виде, при условии известности функциональных коэффициентов
в
общем виде, при условии известности функциональных коэффициентов![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
решена.
,
решена.
17. Функциональные коэффициенты для двух-пяти сред
Рассмотрим функциональные коэффициенты для некоторых частных случаев.
Коэффициенты ![]() ,
, ![]() определяются
из соотношений прямой передачи для первой среды в соответствии с формулами
(99)-(100). Коэффициенты
определяются
из соотношений прямой передачи для первой среды в соответствии с формулами
(99)-(100). Коэффициенты ![]() ,
, ![]() ,
, ![]() ,
, ![]() для среды
для среды ![]() определяются
с помощью соотношений прямой передачи (68)-(69). В этих выражениях для среды с
номером
определяются
с помощью соотношений прямой передачи (68)-(69). В этих выражениях для среды с
номером ![]() функции
функции ![]() определяются
условиями сопряжения между границами с номерами
определяются
условиями сопряжения между границами с номерами ![]() и
и ![]() , то есть при прямом методе имеют вид
(41), а при методе усреднения – вид (50).
, то есть при прямом методе имеют вид
(41), а при методе усреднения – вид (50).
Приведем полученный путем
последовательных подстановок явный вид входящих в (125)-(128) комбинаций из
коэффициентов ![]() ,
, ![]() ,
, ![]() ,
, ![]() для
некоторых значений
для
некоторых значений ![]() .
.
Для двух сред (![]() ):
):
![]() ;
(129)
;
(129)
![]() ;
(130)
;
(130)
![]() ;
(131)
;
(131)
![]() .
(132)
.
(132)
* * * * * * * * * * * * * * * * * * * * * * * * * * * * *
Для трех сред (![]() ):
):
![]() ;
(134)
;
(134)
![]() ;
(135)
;
(135)
![]() .
(136)
.
(136)
* * * * * * * * * * * * * * * * * * * * * * * * * * * * *
Для четырех сред (![]() ):
):
![]()
![]() ; (137)
; (137)
![]()
![]() ; (138)
; (138)
![]()
![]() ; (139)
; (139)
![]()
![]() . (140)
. (140)
* * * * * * * * * * * * * * * * * * * * * * * * * * * * *
Для пяти сред (![]() ):
):
![]()
![]()
![]()
![]() ;
(141)
;
(141)
![]()
![]()
![]()
![]() ;
(142)
;
(142)
![]()
![]()
![]()
![]() ;
(143)
;
(143)
![]()
![]()
![]()
![]() .
(144)
.
(144)
18. Рекуррентные формулы для функциональных коэффициентов
Из структуры полученных выражений
(133)-(144) можно видеть, что последующие комбинации, начиная с ![]() , можно получить из предыдущих с помощью
следующих рекуррентных формул:
, можно получить из предыдущих с помощью
следующих рекуррентных формул:
![]() ;
(145)
;
(145)
![]() ;
(146)
;
(146)
![]() ;
(147)
;
(147)
![]() .
(148)
.
(148)
Получаемые в результате функции ![]() ,
, ![]() ,
, ![]() ,
, ![]() при подстановке
в (125)-(126) позволяют определить функции параметров сред
при подстановке
в (125)-(126) позволяют определить функции параметров сред ![]() ,
, ![]() ,
, ![]() ,
, ![]() , подстановка
которых в (123)-(124) дает выражения амплитуд выходящих из структуры волн
, подстановка
которых в (123)-(124) дает выражения амплитуд выходящих из структуры волн ![]() и
и ![]() через
амплитуды входящих
через
амплитуды входящих ![]() и
и ![]() , что и
является решением исходной задачи.
, что и
является решением исходной задачи.
19. Амплитуды выходящих волн в общем виде
Подставляя (145)-(148) в
(125)-(128), а затем в (123)-(124) и опуская верхний индекс «![]() », запишем амплитуды выходящих волн в
развернутом виде:
», запишем амплитуды выходящих волн в
развернутом виде:
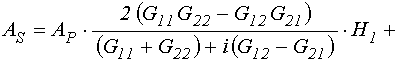
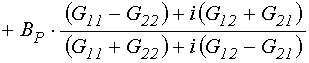 ; (149)
; (149)

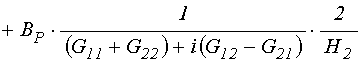 . (150)
. (150)
Выделение в этих выражениях действительной и мнимой частей дает:
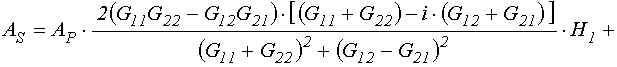
 ; (151)
; (151)
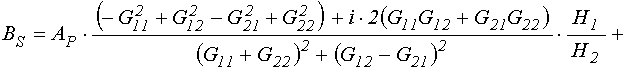
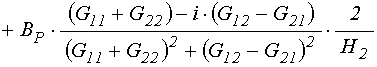 . (152)
. (152)
20. Схема численной реализации метода исключения
Рассмотрим схему численного
расчета для структуры, состоящей из произвольного числа сред ![]() . Пусть заданы координаты границ между
средами
. Пусть заданы координаты границ между
средами ![]() ,
, ![]() , …,
, …,![]() , а также волновые числа во всех средах
, а также волновые числа во всех средах ![]() ,
, ![]() , . . .
,
, . . .
, ![]() . Предположим, что в структуру входят
волны с амплитудами
. Предположим, что в структуру входят
волны с амплитудами ![]() и
и ![]() . Будем
искать амплитуды волн, выходящих из структуры
. Будем
искать амплитуды волн, выходящих из структуры ![]() и
и ![]() , которые в общем случае могут быть
комплексными, то есть содержать фазу выходящих колебаний относительно входящих.
Приведем возможную схему машинного алгоритма в виде совокупности
последовательных шагов.
, которые в общем случае могут быть
комплексными, то есть содержать фазу выходящих колебаний относительно входящих.
Приведем возможную схему машинного алгоритма в виде совокупности
последовательных шагов.
1. ЗАДАНИЕ амплитуд входящих волн
![]() ,
, ![]() .
.
2. ЗАДАНИЕ координат ![]() ,
, ![]() , …,
, …,![]() .
.
3. ЗАДАНИЕ волновых чисел ![]() ,
, ![]() , . . .
,
, . . .
, ![]() .
.
4. ВЫЧИСЛЕНИЕ толщин сред ![]() ,
, ![]() , . . .
,
, . . .
, ![]() .
.
Цикл от ![]() до
до ![]() .
.
![]() .
(153)
.
(153)
5. ВЫЧИСЛЕНИЕ параметров ![]() ,
, ![]() , . . .
,
, . . .
, ![]() . Цикл от
. Цикл от ![]() до
до ![]() .
.
Прямой метод:
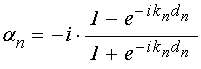 .
(154)
.
(154)
Метод усреднения:
 .
(155)
.
(155)
6. ВЫЧИСЛЕНИЕ ![]() ,
, ![]() .
.
 ;
(156)
;
(156)
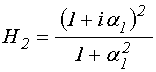 .
(157)
.
(157)
7. ВЫЧИСЛЕНИЕ ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
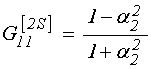 ;
(158)
;
(158)
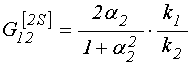 ;
(159)
;
(159)
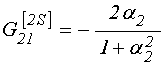 ;
(160)
;
(160)
 .
(161)
.
(161)
8. ВЫЧИСЛЕНИЕ ![]() ,
, ![]() ,
, ![]() ,
, ![]() с
помощью рекуррентных формул. Цикл от
с
помощью рекуррентных формул. Цикл от ![]() до
до ![]() (подпрограмма):
(подпрограмма):
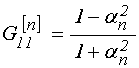 ;
(162)
;
(162)
 ;
(163)
;
(163)
 ;
(164)
;
(164)
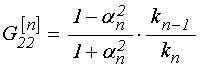 .
(165)
.
(165)
![]() ;
(166)
;
(166)
![]() ;
(167)
;
(167)
![]() ;
(168)
;
(168)
![]() .
(169)
.
(169)
9. ВЫЧИСЛЕНИЕ ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
 ;
(170)
;
(170)
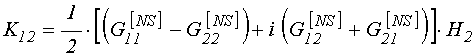 ;
(171)
;
(171)
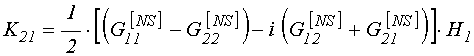 ;
(172)
;
(172)
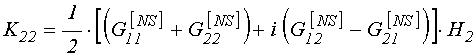 .
(173)
.
(173)
10. ВЫЧИСЛЕНИЕ амплитуд выходящих
волн ![]() ,
, ![]() .
.
 ;
(174)
;
(174)
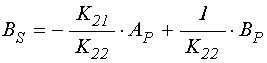 .
(175)
.
(175)
11. ВЫВОД полученных значений ![]() ,
, ![]() .
.
21. Пример использования метода исключения для исследования распространения волн в неоднородной структуре
Проиллюстрируем теперь работу метода исключения на частном примере, в качестве которого обратимся к задаче о распространении волны в неоднородной среде с линейным изменением волнового числа по координате.
Пусть рассматриваемая
неоднородная среда ограничена координатами ![]() и
и ![]() , то есть имеет полную толщину
, то есть имеет полную толщину ![]() , а волновое число внутри нее меняется по
линейному закону:
, а волновое число внутри нее меняется по
линейному закону:
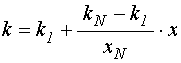 ,
(176)
,
(176)
где ![]() и
и ![]() – волновые числа при
– волновые числа при ![]() и
и ![]() соответственно.
соответственно.
Представим среду в виде
многослойной структуры длиной ![]() , заключенной в
пределах от
, заключенной в
пределах от ![]() до
до ![]() ,
состоящей из
,
состоящей из ![]() однородных сред одинаковой толщины. Будем
полагать, что волновое число с такой структуре меняется ступенчатым образом
так, что для среды с номером
однородных сред одинаковой толщины. Будем
полагать, что волновое число с такой структуре меняется ступенчатым образом
так, что для среды с номером ![]() , где
, где ![]() , то есть при
, то есть при ![]() волновое
число сохраняется постоянным равным
волновое
число сохраняется постоянным равным
![]() .
(177)
.
(177)
При этом длины всех ступенек
изменения волнового числа одинаковы и равны ![]() , а
высоты также одинаковы и составляют
, а
высоты также одинаковы и составляют ![]() .
.
В работе [23] получен критерий применимости приближения линейной неоднородности ступенчатой функцией, в частности показано, что такое приближение является достаточно корректным тогда, когда минимальная длина волны в структуре превышает полную длину структуры не менее чем в два раза.
В работе [21] показано, что метод
усреднения дает достаточно корректные результаты тогда, когда толщина
отдельного слоя не превышает ![]() от длины волны в этом
слое.
от длины волны в этом
слое.
Рассмотрим корректность
поставленной задачи с этих двух точек зрения на конкретном численном примере
десятислойной структуры (![]() ), волновое число в
которой меняется от
), волновое число в
которой меняется от ![]() до
до ![]() с
шагом
с
шагом ![]() . Минимальная длина волны соответствует
максимальному значению волнового числа
. Минимальная длина волны соответствует
максимальному значению волнового числа ![]() ,
откуда получаем:
,
откуда получаем: ![]() . Это означает, что предел
корректности ступенчатого приближения для полной длины структуры равен
. Это означает, что предел
корректности ступенчатого приближения для полной длины структуры равен ![]() . Предел применимости метода усреднения
для одного слоя структуры составляет
. Предел применимости метода усреднения
для одного слоя структуры составляет ![]() , то есть этот метод
работает удовлетворительно только тогда, когда полная длина структуры не
превышает
, то есть этот метод
работает удовлетворительно только тогда, когда полная длина структуры не
превышает ![]() .
.
Для этого случая на рис.6 при ![]() ,
, ![]() показаны
зависимости волнового числа
показаны
зависимости волнового числа ![]() и параметра
и параметра ![]() от координаты
от координаты ![]() при
прямом методе (сплошные линии) и методе усреднения (пунктир) для трех различных
длин структуры в целом:
при
прямом методе (сплошные линии) и методе усреднения (пунктир) для трех различных
длин структуры в целом: ![]() (а),
(а), ![]() (б) и
(б) и ![]() (в).
(в).
Из рис.6 видно, что при ![]() (а) параметры
(а) параметры ![]() ,
полученные обоими методами, полностью совпадают. При
,
полученные обоими методами, полностью совпадают. При ![]() совпадение
наблюдается только до
совпадение
наблюдается только до ![]() , после чего метод усреднения
дает несколько заниженные значения. Отмеченное значение
, после чего метод усреднения
дает несколько заниженные значения. Отмеченное значение ![]() соответствует
соответствует
![]() или
или ![]() , что
несколько превышает критическое значение
, что
несколько превышает критическое значение ![]() , то
есть условия применимости метода усреднения здесь уже серьезно нарушаются, что
и обусловливает наблюдаемое отклонение. При
, то
есть условия применимости метода усреднения здесь уже серьезно нарушаются, что
и обусловливает наблюдаемое отклонение. При ![]() о каком-то
соответствии можно говорить только не более чем до
о каком-то
соответствии можно говорить только не более чем до ![]() , после
чего параметры
, после
чего параметры ![]() , полученные разными методами,
отличаются в два и более раз, то есть метод усреднения становится совершенно неприменимым.
, полученные разными методами,
отличаются в два и более раз, то есть метод усреднения становится совершенно неприменимым.

Рис.6. Зависимости волнового числа ![]() (верхний ряд) и параметра
(верхний ряд) и параметра ![]() (нижний ряд) от координаты
(нижний ряд) от координаты ![]() при прямом методе (сплошные линии) и
методе усреднения (пунктир). а –
при прямом методе (сплошные линии) и
методе усреднения (пунктир). а – ![]() ; б –
; б – ![]() ; в –
; в – ![]() .
.
Рассмотрим теперь для той же
структуры работу обоих методов при различной полной длине структуры. Для этого
случая на рис.7 показаны зависимости амплитуд выходящих волн ![]() (кривые
(кривые ![]() ,
, ![]() ) и
) и ![]() (кривые
(кривые
![]() ,
, ![]() ) от
полной длины структуры
) от
полной длины структуры ![]() при
при ![]() ,
, ![]() , полученные прямым методом (сплошные
линии) и методом усреднения (пунктир). Стрелкой внизу отмечено критическое
значение полной длины структуры
, полученные прямым методом (сплошные
линии) и методом усреднения (пунктир). Стрелкой внизу отмечено критическое
значение полной длины структуры ![]() , выше которого условия
применимости ступенчатого приближения нарушаются.
, выше которого условия
применимости ступенчатого приближения нарушаются.
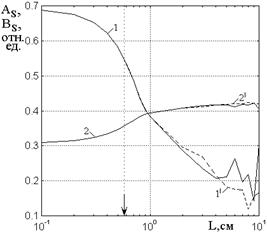
Рис.7. Зависимости амплитуд выходящих
волн: отраженной ![]() (
(![]() ,
, ![]() ) и проходящей
) и проходящей ![]() (
(![]() ,
, ![]() ) при
) при ![]() ,
, ![]() от
полной длины структуры
от
полной длины структуры ![]() , полученные методами: прямым
(сплошные линии) и усреднения (пунктир).
, полученные методами: прямым
(сплошные линии) и усреднения (пунктир).
Из рис.7 видно, что при ![]() все кривые претерпевают определенный
излом, то есть их наклон заметно меняется. Это означает, что ступенчатое приближение
еще продолжает удовлетворительно работать до величины порядка
все кривые претерпевают определенный
излом, то есть их наклон заметно меняется. Это означает, что ступенчатое приближение
еще продолжает удовлетворительно работать до величины порядка ![]() от критического значения, после чего,
особенно с
от критического значения, после чего,
особенно с ![]() (больше критического почти в четыре раза)
зависимости приобретают изломанный характер, подобный наблюдавшемуся в работе
[23].
(больше критического почти в четыре раза)
зависимости приобретают изломанный характер, подобный наблюдавшемуся в работе
[23].
Метод усреднения с точностью
порядка ![]() работает до
работает до ![]() , после
чего о соответствии до
, после
чего о соответствии до ![]() можно говорить вплоть до
можно говорить вплоть до ![]() , а затем ошибка, особенно по амплитуде
отраженной волны, резко возрастает. Таким образом, и здесь корректность метода
усреднения ожидаемому критерию, установленному в работе [21] полностью соответствует.
, а затем ошибка, особенно по амплитуде
отраженной волны, резко возрастает. Таким образом, и здесь корректность метода
усреднения ожидаемому критерию, установленному в работе [21] полностью соответствует.
22. Обобщение для электромагнитных волн
Проведенное рассмотрение выполнено на основе одномерной волны, однако оно может быть обобщено на случай волн другой природы, в частности, электромагнитных, например так, как это сделано в работах [13-15]. Так, для случая нормального падения достаточно во всех выражениях, содержащих волновое число, кроме показателей экспонент, произвести замены:
![]() ,
(178)
,
(178)
где ![]() ,
, ![]() - импеданс пустого пространства, а
- импеданс пустого пространства, а ![]() и
и ![]() –
магнитная и диэлектрическая проницаемости
–
магнитная и диэлектрическая проницаемости ![]() -го
слоя.
-го
слоя.
Для наклонного падения волны с продольной (вертикальной) поляризацией надо произвести замену:
![]() ,
(179)
,
(179)
в случае поперечной (горизонтальной) поляризации замену:
![]() ,
(180)
,
(180)
а также заменить экспоненту:
![]() ,
(181)
,
(181)
где ![]() – угол
распространения (преломления) волны в
– угол
распространения (преломления) волны в ![]() -м
слое, определяемый законом Снеллиуса [4,13]:
-м
слое, определяемый законом Снеллиуса [4,13]:
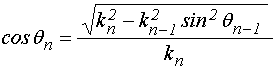 .
(182)
.
(182)
При этом все остальные выражения остаются без изменений.
Так вид волновых функций (3)-(4) не меняется, а уравнения (6)-(7), например, для случая нормального падения, заменяются следующими:
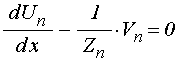 ;
(183)
;
(183)
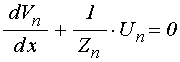 .
(184)
.
(184)
Выражение (41) для ![]() , соответствующее прямому методу, не
меняется, а аналогичное выражение (50) для метода усреднения принимает вид:
, соответствующее прямому методу, не
меняется, а аналогичное выражение (50) для метода усреднения принимает вид:
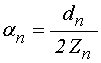 .
(185)
.
(185)
Условия сопряжения, выражаемые через ![]() , не меняются, граничные условия (53) остаются
прежними, а (55) принимают вид:
, не меняются, граничные условия (53) остаются
прежними, а (55) принимают вид:
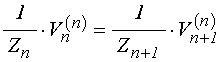 .
(186)
.
(186)
Соотношения прямой передачи (62)-(63) принимают вид.:
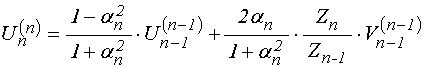 ;
(187)
;
(187)
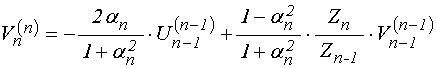 . (188)
. (188)
Функции (64) и (66) остаются прежними, а (65) и (67) принимают вид:
 ;
(189)
;
(189)
 .
(190)
.
(190)
Аналогичные изменения претерпевают остальные функции.
В случае наклонного падения волновые функции (3)-(4) принимают вид:
![]() ;
(191)
;
(191)
![]() .
(192)
.
(192)
Параметры ![]() для
прямого метода принимают вид:
для
прямого метода принимают вид:
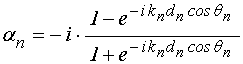 ;
(193)
;
(193)
для метода усреднения при продольной поляризации:
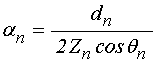 ;
(194)
;
(194)
при поперечной поляризации:
 .
(195)
.
(195)
Граничное условие (55) для продольной поляризации принимает вид:
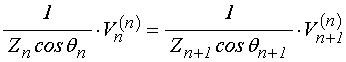 ;.
(196)
;.
(196)
и соответственно для поперечной поляризации:
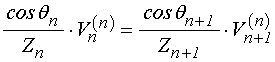 .
(197)
.
(197)
Аналогичные изменения претерпевают остальные формулы.
Выводы
Предложен простой метод расчета амплитуд отраженной и проходящей волн при падении двух встречных волн на многослойную структуру со ступенчатой неоднородностью, названный «методом исключения». Метод состоит во ведении в рассмотрение двух волновых функций, одна из которых является суммой встречных волн, а другая – частным от деления производной от первой на волновое число. Вся структура разбивается на ячейки, каждая из которых включает в себя одну среду и одну границу, находятся соотношения между упомянутыми функциями на внешних сторонах каждой ячейки, которые сшиваются простым «прикладыванием» друг к другу, в результате чего амплитуды внутренних волн взаимно исключаются. Решение получаемой в результате системы из двух линейных уравнений позволяет найти амплитуды выходящих из структуры волн через амплитуды входящих.
Получены условия сопряжения, связывающие амплитуды входящих и выходящих волн для отдельного слоя при использовании методов прямого и усреднения. На их основе найдены соотношения прямой передачи, связывающие амплитуды волн в предыдущей ячейке с амплитудами в последующей. Получены рекуррентные формулы, позволяющие находить функциональные коэффициенты связи, определяющие амплитуды выходящих из структуры волн через амплитуды волн, в нее входящих. Приведен явный вид функциональных коэффициентов для структур, содержащих от двух до пяти сред. Для произвольного числа слоев получены выраженные через функциональные коэффициенты соотношения между амплитудами входящих и выходящих волн.
Приведена схема численной реализации метода исключения, пригодная для создания машинного алгоритма решения задачи. Работа метода продемонстрирована на примере многослойной структуры из десяти сред. Показана возможность получения амплитуд выходящих волн через амплитуды входящих. Подтверждено условие применимости ступенчатого приближения для неоднородной среды, состоящее в необходимости превышения минимальной длиной волны полной длины структуры в два раза. Подтверждено условие применимости метода усреднения, устанавливающее верхний предел допустимой толщины слоя, равный 0,35 от минимальной длины волны в этом слое.
В соответствии с общностью волновых процессов различной природы, даны рекомендации для применения метода исключения к задачам о распространении электромагнитных волн для случаев нормального и наклонного падения.
Работа выполнена при финансовой поддержке РФФИ (грант № 13-02-01401-а).
1. Рэлей Дж.У. Теория звука. Т.1,2. М.: ИЛ. 1955.
2. Бреховских Л.М. // ЖТФ. 1949. Т.19. №10. С.1126.
3. Розенберг Г.В. Оптика тонкослойных покрытий. М.: Гос.изд.физ-мат.лит. 1958.
4. Борн М., Вольф Э. Основы оптики. М.: Наука. 1970.
5. Бреховских Л.М. Волны в слоистых средах. М.: Наука. 1973.
6. Кизель В.А. Отражение света. М.: Наука. 1973.
7. Джеррард А., Бёрч Дж.М. Введение в матричную оптику.
М.: Наука. 1978.
8. Бреховских Л.М., Годин О.А. Акустика слоистых сред. М.: Наука. 1989.
9. Oksanen M.I., Hanninen J., Tretyakov S.A. // IEEE Proc.H. 1991. V.138. №7. P.513.
10. Sarychev A.K., Bergman D.J., Yagil Y. // PR(B). 1995. V.51. №8. P.5366.
11. Шварцбург А.Б. // УФН. 2000. Т.170. №12. С.1297.
12. Шалин А.С., Моисеев С.Г. // Оптика и спектроскопия. 2009. Т.106. №6. С.1004.
13. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2010. Т.55. №2. С.133.
14. Антонец И.В., Щеглов В.И. Распространение волн через тонкие слои и пленки. Сыктывкар: ИПО СыктГУ. 2010.
15. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть первая. Прямой метод. Сыктывкар: ИПО СыктГУ. 2011.
16. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть вторая. Метод матрицы. Сыктывкар: ИПО СыктГУ. 2012.
17. Антонец И.В., Щеглов В.И. Распространение волн через многослойные структуры. Часть третья. Метод импеданса.
Сыктывкар: ИПО СыктГУ. 2012.
18. Конторович М.И., Черепанов А.С. // РЭ. 1985. Т.30. №8. С.1543.
19. Конторович М.И., Третьяков С.А. // РЭ. 1986. Т.31. №6. С.1110.
20. Халиуллин Д.Я., Третьяков С.А. // РЭ. 1998. Т.43. №1. С.16.
21. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2007. Т.52. №4. С.403.
22. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2008. Т.53. №4. С.389.
23. Антонец И.В., Котов Л.Н., Шавров В.Г., Щеглов В.И. // РЭ. 2012. Т.57. №1. С.67.