УДК 621.396.49
КВАЗИОПТИМАЛЬНЫЙ АЛГОРИТМ ПРИЕМА СИГНАЛОВ ШИРОКОПОЛОСНЫХ СИСТЕМ СВЯЗИ НА БАЗЕ МУЛЬТИМАРКОВО-ПОЛИГАУССОВЫХ ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ
С. В. Козлов, Ш. М. Чабдаров
Казанский национальный исследовательский технический университет им. А.Н. Туполева
Статья получена 9 апреля 2014 г., после доработки - 25 апреля 2014 г.
Аннотация. Статья посвящена анализу возможных путей построения совместных алгоритмов приёма сигналов широкополосных систем связи, имеющих ограничения по вычислительной сложности, и синтезу отвечающего этим требованиям квазиоптимального алгоритма на базе нового подкласса полигауссовых моделей – мультимарково-полигауссовых моделей. Разработанный алгоритм обеспечивает линейную зависимость числа каналов и полиномиальную зависимость количества элементарных арифметических операций от размерности сигнала, которая определяется произведением числа сигналов на количество лучей, учитываемых при их распространении. В работе анализируется и подтверждается эффективность синтезированного алгоритма для сигналов стандарта CDMA One.
Ключевые слова: Марковские процессы, смеси, полигауссовы, CDMA, мультимарково-полигауссова модель, совместный приём, разрешение сигналов, линейная нестационарная фильтрация, Калман.
Abstract: This article describes analysis of the possible ways to build joint algorithms for reception of wideband communication systems that are a limited by the computational complexity and synthesis of the suboptimal algorithm based on a new subclass of poly-Gaussian models - multi-Markov poly-Gaussian. The developed algorithm provides a linear dependence of the number of channels and a polynomial dependence of the elementary arithmetic operation`s count on the dimension of the signal, which is determined by multiplication of the number of signals by the amount of propagation rays. In work efficiency of the synthesized algorithm for signals CDMA One standard is analyzed and confirmed.
Введение
Для адекватного описания сигнально-помеховой обстановки (СПО) в негауссовых каналах успешно применяются смеси стандартных распределений в виде полигауссовых моделей общего вида, а также марково-смешанных полигауссовых, суммарно-смешанных полигауссовых и мультимарково-полигауссовых (ММ-ПГ) [1,2] моделей. Однако все оптимальные алгоритмы совместного приёма сигналов, построенные на базе этих моделей, обладают общим недостатком: количество каналов обработки в них по показательному закону зависит от количества сигналов, что сильно ограничивает область их практического применения.
Рассмотренный в работе [3] способ реализации разрешения сигналов с линейной вычислительной сложностью алгоритма работает лишь в синхронных каналах при детерминированной модели полезных сигналов. Эти требования в городских условиях с многолучевым распространением радиоволн не обеспечиваются.
Таким образом, актуальной задачей является разработка квазиоптимального алгоритма, позволяющего уйти от показательной зависимости числа каналов от числа сигналов.
Постановка задачи
Целью работы является синтез квазиоптимального алгоритма приёма широкополосных сигналов на базе ММ-ПГ модели описания СПО, обеспечивающего меньшую, чем показательная, скорость возрастания зависимости числа каналов от количества сигналов.
Выбор модели обусловлен её способностью адекватно описывать СПО при меньшем, чем у других ПГ моделей количестве компонент [1].
Показательная зависимость
количества каналов от количества сигналов для этой модели объясняется
зависимостью базисных векторов сигналов, сформированных на длительности
кодового символа ![]() , от реализации вектора передаваемых
кодовых символов
, от реализации вектора передаваемых
кодовых символов ![]() , где
, где ![]() -
-
![]() -ый кодовый символ
-ый кодовый символ ![]() -го
сигнала
-го
сигнала ![]() .
.
При сокращении интервала ![]() количество возможных комбинаций будет
снижаться и при достижении интервала наблюдения в один отсчёт, окажется равным
единице.
количество возможных комбинаций будет
снижаться и при достижении интервала наблюдения в один отсчёт, окажется равным
единице.
Однако непосредственное применение такого подхода не приводит к положительным результатам в связи с уменьшением энергии сигнала на меньшем интервале наблюдения, приводящим к снижению отношения сигнал/шум, и потерей ортогональности сигналов в широкополосных системах.
Для преодоления указанного ограничения широко используются марковские вероятностные модели [4], которые применяются в ММ-ПГ модели для описания отдельных компонент.
Таким образом, задача синтеза квазиоптимального алгоритма совместного приёма сигналов может быть решена путём модернизации оптимального ММ-ПГ алгоритма с уменьшением интервала анализа до одного отсчёта.
Описание алгоритма
Сформируем сигнальную
модель реализации отсчетов входного колебания ![]() сигналов,
имеющих
сигналов,
имеющих ![]() лучей, для
лучей, для ![]() -ого
кодового символа. Обозначим как
-ого
кодового символа. Обозначим как ![]() вектор комбинации элементарных
компонент
вектор комбинации элементарных
компонент ![]() , а
, а ![]() -
вектор комбинаций номеров предсказаний
-
вектор комбинаций номеров предсказаний ![]() . Тогда
для вектора комбинаций элементарных компонент
. Тогда
для вектора комбинаций элементарных компонент ![]() ,
, ![]() (
(![]() ), уравнения
наблюдения и сообщения векторного фильтра Калмана [5] с матрицей предсказания
), уравнения
наблюдения и сообщения векторного фильтра Калмана [5] с матрицей предсказания ![]() будут иметь вид:
будут иметь вид:
![]() ,
, ![]() , (1)
, (1)
где ![]() -
- ![]() -ый отсчёт реализации входного колебания
для
-ый отсчёт реализации входного колебания
для ![]() -ого кодового символа,
-ого кодового символа, ![]() - вектор модуляции,
- вектор модуляции, ![]() - вектор оценок квадратурных амплитуд
сигналов с ковариационной матрицей
- вектор оценок квадратурных амплитуд
сигналов с ковариационной матрицей ![]() ,
, ![]() -
- ![]() -ый
отсчёт белого гауссова шума измерения с дисперсией
-ый
отсчёт белого гауссова шума измерения с дисперсией ![]() ,
, ![]() - вектор отсчётов формирующего шума с
ковариационной матрицей
- вектор отсчётов формирующего шума с
ковариационной матрицей ![]() .
.
Для учёта переходных
процессов, возникающих при смене кодовых символов с ![]() на
на ![]() , в момент обработки последнего отсчёта
, в момент обработки последнего отсчёта ![]() , соответствующие ему компоненты
ковариационной матрицы формирующего шума корректируются:
, соответствующие ему компоненты
ковариационной матрицы формирующего шума корректируются:
![]() , (2)
, (2)
где ![]() -
дисперсия переходного процесса,
-
дисперсия переходного процесса, ![]() - единичная матрица, а
- единичная матрица, а
![]() - диагональная матрица, имеющая на
главной диагонали элементы
- диагональная матрица, имеющая на
главной диагонали элементы ![]() , равные нулю для
последних отсчётов
, равные нулю для
последних отсчётов ![]() и единице в противном случае.
и единице в противном случае.
Реализуем оценку отсчётов входного колебания с помощью алгоритма векторного фильтра Калмана, приведённого в [5]:
![]() ,
, 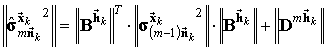 ,
, ![]() ,
, ![]() ,
, 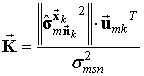 ,
, ![]() ,
, ![]() ,
, ![]() .
(3)
.
(3)
Плотность вероятности итоговой оценки можно определить согласно выражению:
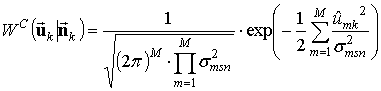 . (4)
. (4)
Для описания взаимосвязи
компонент последовательных кодовых символов в разрабатываемом алгоритме
предлагается использовать ординарную цепь Маркова, заданную вектором начальных
вероятностей ![]() с элементами вида
с элементами вида ![]() и
матрицей переходных вероятностей
и
матрицей переходных вероятностей ![]() , состоящей из условных
вероятностей
, состоящей из условных
вероятностей ![]() . Такое решение позволяет снизить
количество компонент, необходимых для реализации алгоритма [1]. Для этого
случая с использованием выражений для ММ-ПГ, приведённых в [1], можно получить
формулы для рекуррентной оценки апостериорных вероятностей реализации
компонент:
. Такое решение позволяет снизить
количество компонент, необходимых для реализации алгоритма [1]. Для этого
случая с использованием выражений для ММ-ПГ, приведённых в [1], можно получить
формулы для рекуррентной оценки апостериорных вероятностей реализации
компонент:
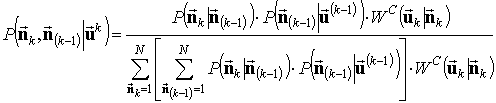 . (5)
. (5)
Для ![]() компоненты с истекшей историей
объединяются в одну компоненту:
компоненты с истекшей историей
объединяются в одну компоненту:
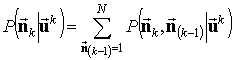 . (6)
. (6)
На основе полученных значений производится определение весовых коэффициентов векторов комбинаций элементарных компонент, итоговой плотности вероятности и численных значений параметров объединенных компонент:
 , (7)
, (7)
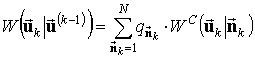 , (8)
, (8)
 , (9)
, (9)
 . (10)
. (10)
Для равномерного
распределения вероятностей кодовых символов на основе критерия максимального
правдоподобия правило принятия решения о передаваемом ![]() -ом
кодовом символе
-ом
кодовом символе ![]() -го сигнала
-го сигнала ![]() будет иметь вид:
будет иметь вид:
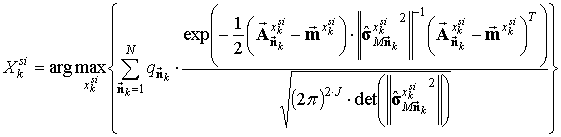 , (11)
, (11)
где ![]() -
вектор математических ожиданий кодового символа
-
вектор математических ожиданий кодового символа ![]() , а
, а 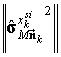 - его ковариационная матрица,
формирующаяся из относящихся к нему элементов матрицы
- его ковариационная матрица,
формирующаяся из относящихся к нему элементов матрицы ![]() .
.
Параметры алгоритма могут быть определены в условиях априорной неопределённости согласно формулам из [1].
Результаты моделирования
Оценка эффективности синтезированного алгоритма приема производилась для сигналов сети сотовой связи стандарта CDMA One. С использованием программного комплекса CDMA Analyzer осуществлялась эмуляция приёма записанных сигналов с применением классического алгоритма приёма, использующего моногауссову модель, а также синтезированных на базе ММ-ПГ модели оптимального и квазиоптимального алгоритмов. Полученные результаты приведены в таблице 1.
Табл. 1. Зависимость полученных параметров от алгоритма и условий приёма
|
Параметры |
Условия приёма |
Классический алгоритм приёма |
ММ-ПГ квазиоптимальный алгоритм |
ММ-ПГ оптимальный алгоритм |
|
Дисперсия пилот тона |
Стационарный |
0.0027 |
0.0006 |
0.0008 |
|
В движении |
0.0045 |
0.0007 |
0.0019 |
|
|
Дисперсия «остаточного шума» |
Стационарный |
1268 |
924 |
970 |
|
В движении |
1488 |
1185 |
1188 |
|
|
Вероятность ошибки бита в канале синхронизации |
Стационарный |
0.0096 |
0.0063 |
0.0038 |
|
В движении |
0.0083 |
0.0045 |
0.0026 |
Заключение
На основе полученных результатов можно сделать вывод об эффективности разработанного алгоритма при обеспечении линейной зависимости количества его каналов и общей кубической зависимости количества базовых операций от количества сигналов.
1. Козлов С.В. Мультимарково-полигауссовские модели и алгоритмы в широкополосных системах // Нелинейный мир. -2011. - Том №9.- №11.С.716-726.
2. Козлов С.В., Надеев А.Ф., Файзуллин Р.Р. Мультимарково-полигауссовы алгоритмы в широкополосных системах связи Вестник Казанского государственного технического университета им. А.Н. Туполева. 2012. № 4-2. С. 171-174.
3. Чабдаров Ш.М., Надеев А.Ф., Чикрин Д.Е., Файзуллин Р.Р. Линейный по сложности алгоритм полного разрешения сигналов на основе полигауссовых вероятностных моделей // Вестник Марийского государственного технического университета, серия «Радиотехнические и инфокоммуникационные системы»– 2011. №1. С.3-12
4. Тихонов В.И., Кульман Н.К. Нелинейная фильтрация и квазикогерентный приём сигналов. – М. Сов. Радио, 1975. – 705с.
5. Тихонов В.И., Харисов В.Н. Статистический анализ и синтез радиотехнических устройств и систем: Учеб. Пособие для вузов. М.: Радио и связь, 1991.-608с.