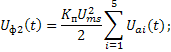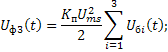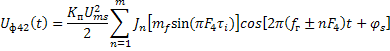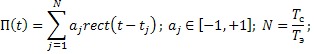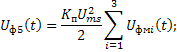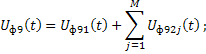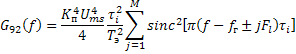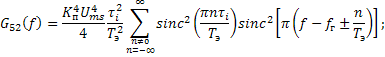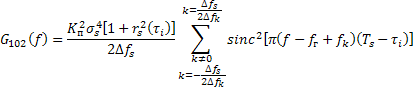УДК 621.391.037
Классификатор связных сигналов на основе комбинации корреляционных и спектральных алгоритмов
А. П. Дятлов, А. Н. Шостак
Институт радиотехнических систем и управления инженерно-технологической академии Южного Федерального Университета
Статья получена 27 марта 2014 г.
Аннотация. Исследованы алгоритм и структура классификатора связных сигналов, инвариантного к неопределенности о несущей частоте сигнала и обладающего расширенными функциональными возможностями. Исследованы особенности функционирования классификатора при использовании различных информативных признаков. Представлен стенд для моделирования процесса распознавания и оптимизации основных характеристик классификатора.
Ключевые слова: экспресс-анализ, радиомониторинг, классификатор, корреляционно-фильтровое устройство, параллельный спектроанализатор, вид модуляции, вероятность ошибочного решения, отношение сигнал/помеха.
Abstract. Structures and algorithms classifier communication signals, which is invariant to uncertainty about the carrier frequency signal and has advanced features, are investigated. Features of the functioning of the classifier using a variety of informative signs are investigated. A stand for modeling the recognition process and optimization of the basic characteristics of the classifier is presented.
Keywords: express analysis, radio monitoring, classifier, correlation-filtration device, parallel spectrum analyzer, modulation type, the probability of a wrong decision, signal-to-noise ratio.
Стремительное развитие электронных компонентов приводит к появлению новых, ранее недоступных радиоэлектронных систем (РЭС), которые, благодаря своей дешевизне и компактности, внедряются во многие сферы человеческой деятельности. В свою очередь, это существенно усложняет радиоэлектронную обстановку (РО) и порождает проблемы с обеспечением электромагнитной совместимости (ЭМС).
Поэтому проведение радиочастотного мониторинга (РМ) в условиях наличия кратковременно работающих РЭС требует от экспресс-анализаторов (ЭА) высокого быстродействия и достоверности. Для увеличения эффективности обработки информации современные ЭА используют автоматические классификаторы сигналов.
Задача классификации вида модуляции сигнала относится к актуальным проблемам РМ и может решаться при использовании спектральных, корреляционных и комбинированных алгоритмов обработки информации. К недостаткам спектральных классификаторов следует отнести то обстоятельство, что они в основном применяются при классификации непрерывных сигналов [1], а к недостаткам корреляционных классификаторов следует отнести то обстоятельство, что они в основном применяются при классификации импульсных сигналов [1].
В данной статье исследуется алгоритм и структура классификатора связных сигналов (КСС) независимого от априорной неопределённости об их несущей частоте и обеспечивающего оперативную классификацию широкого перечня как импульсных, так и непрерывных связных сигналов с различными видами модуляции.
КСС помещается на выходе УПЧ в приёмной части ЭА.
Структурная схема КСС
приводится на рис. 1, где КФУ – корреляционно-фильтровое устройство; ![]() ,
, ![]() ,
, ![]() – полосовые фильтры; ПЛЗ – перестраиваемая
линия задержки; П – перемножитель; Г – гетеродин; ПСА – параллельный
спектроанализатор; Упр – управитель; РУ – решающее устройство.
– полосовые фильтры; ПЛЗ – перестраиваемая
линия задержки; П – перемножитель; Г – гетеродин; ПСА – параллельный
спектроанализатор; Упр – управитель; РУ – решающее устройство.
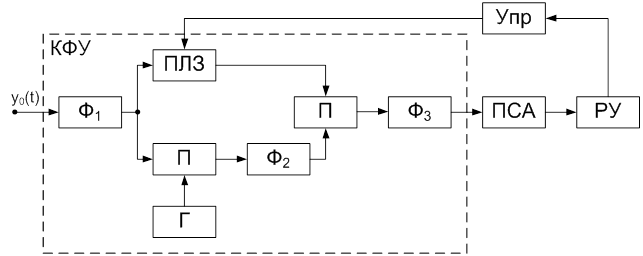
Рис. 1. Структурная схема КСС
Принцип действия КСС заключается в следующем. КФУ выполняет перенос входного сигнала на фиксированную частоту и осуществляет трансформацию его спектрального распределения, позволяющую ПСА выделить необходимые информативные признаки и принять решение о типе модуляции сигнала.
Для упрощения анализа
будем полагать, что в процессе РМ будут использованы различные виды селекции
(поляризационная, пространственная, частотная или временная), которые обеспечат
сведение многокомпонентной РО к двухкомпонентной модели РО, чтобы на вход
полосового фильтра ![]() подавался двухкомпонентный процесс
подавался двухкомпонентный процесс
![]()
где ![]() – сигнал с неизвестным видом
модуляции
– сигнал с неизвестным видом
модуляции ![]() и совокупностью сопутствующих
параметров
и совокупностью сопутствующих
параметров ![]() , характеризующими уровень
априорной неопределённости, влияние мультипликативной помехи и т.д.;
, характеризующими уровень
априорной неопределённости, влияние мультипликативной помехи и т.д.;
![]() – гауссовая стационарная помеха с
известной автокорреляционной функцией
– гауссовая стационарная помеха с
известной автокорреляционной функцией
![]()
где ![]() – дисперсия
– дисперсия ![]() ;
; ![]() – полоса пропускания УПЧ;
– полоса пропускания УПЧ; ![]() – промежуточная частота;
– промежуточная частота; ![]() –
количество классифицируемых видов модуляции.
–
количество классифицируемых видов модуляции.
После принятых
допущений рассмотрим подробнее процесс обработки сигнала ![]() в КФУ. Для этого
проведём анализ напряжений на выходах его функциональных узлов (ФУ):
в КФУ. Для этого
проведём анализ напряжений на выходах его функциональных узлов (ФУ):
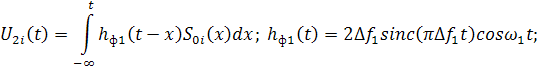
![]()
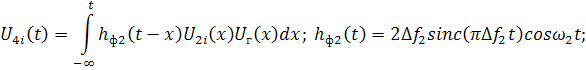
![]()
где
![]() – напряжение на выходе полосового
фильтра
– напряжение на выходе полосового
фильтра ![]() ;
; ![]() – напряжение на выходе ПЛЗ;
– напряжение на выходе ПЛЗ; ![]() – напряжение на выходе полосового
фильтра
– напряжение на выходе полосового
фильтра ![]() ;
; ![]() –
напряжение гетеродина Г;
–
напряжение гетеродина Г; ![]() – коэффициент передачи ПЛЗ по
напряжению;
– коэффициент передачи ПЛЗ по
напряжению; ![]() – величина задержки, вносимой ПЛЗ;
– величина задержки, вносимой ПЛЗ;
![]() – импульсная реакция фильтров
– импульсная реакция фильтров ![]() и
и ![]() ;
; ![]() – средняя частота фильтров
– средняя частота фильтров ![]() и
и ![]() ;
; ![]() – полоса пропускания фильтров
– полоса пропускания фильтров ![]() и
и ![]() ;
; ![]() – частота гетеродина Г.
– частота гетеродина Г.
На выходе КФУ после полосового
фильтра ![]() получаем напряжение,
представляющее трансформированное спектральное распределение сигнала
получаем напряжение,
представляющее трансформированное спектральное распределение сигнала

![]()
где ![]() – напряжение на выходе полосового
фильтра
– напряжение на выходе полосового
фильтра ![]() , при приёме сигнала j-го
класса;
, при приёме сигнала j-го
класса; ![]() – импульсная реакция фильтра
– импульсная реакция фильтра ![]() ;
; ![]() – полоса пропускания фильтра
– полоса пропускания фильтра ![]() ;
; ![]() – средняя частота фильтра
– средняя частота фильтра ![]() ;
; ![]() –
номер класса сигнала.
–
номер класса сигнала.
Трансформированное
спектральное распределение сигнала позволяет выявить в нём необходимые информативные
признаки о виде модуляции. Для этого выполним расчёт временного и спектрального
представления напряжения ![]() при приёме сигнала j-го
класса. Полученные результаты приводятся в табл. 1 и 2. Описание перечня
классифицируемых связных сигналов приводится в табл. 1.
при приёме сигнала j-го
класса. Полученные результаты приводятся в табл. 1 и 2. Описание перечня
классифицируемых связных сигналов приводится в табл. 1.
Анализ спектральных
представлений, приведённых в табл. 2, указывает на то, что работа КФУ позволяет
вскрывать и использовать в качестве информативных признаков ранее недоступные
спектральные компоненты, а их уровень, значение частоты и ширина спектра
зависят от величины временного сдвига ![]() , вносимого ПЛЗ [2].
, вносимого ПЛЗ [2].
Поэтому, с целью
оптимизации величины задержки ![]() и повышения надёжности
классификации, в КФУ выполняется вначале панорамная перестройка ПЛЗ в
соответствии со следующим выражением:
и повышения надёжности
классификации, в КФУ выполняется вначале панорамная перестройка ПЛЗ в
соответствии со следующим выражением:
![]()
где ![]() – нижняя и верхняя границы
диапазона изменения задержки, вносимой ПЛЗ;
– нижняя и верхняя границы
диапазона изменения задержки, вносимой ПЛЗ; ![]() – шаг перестройки ПЛЗ;
– шаг перестройки ПЛЗ; ![]() – количество шагов перестройки
ПЛЗ;
– количество шагов перестройки
ПЛЗ; ![]() – интервал
корреляции помехи;
– интервал
корреляции помехи; ![]() – длительность шага и цикла
перестройки ПЛЗ.
– длительность шага и цикла
перестройки ПЛЗ.
Таблица 1. Временное представление сигналов на входе и выходе КФУ
|
Класс сигнала |
Входной процесс |
Выходной процесс |
|
1. ГС – гармонический сигнал |
|
|
|
2. АМС – амплитудномо-дулированный сигнал |
|
|
|
3. БМС – балансномоду-лированный сигнал |
|
|
|
4. ЧМГ – частотно-моду-лированный сигнал с гармонической модуля-цией |
|
|
|
5. ФМС – фазоманипули-рованный сигнал |
|
|
|
6. ЛЧМС1 – импульсный линейночастотномодули-рованный сигнал с нара-стающей или спадающей частотой |
|
|
|
7. ЛЧМС2 – линейноча-стотномодулированный сигнал с несимметрич-ным пилообразным зако-ном изменения частоты |
|
|
|
8. ЛЧМС3 – линейноча-стотномодулированный сигнал с симметричным пилообразным законом изменения частоты |
|
|
|
9. СППРЧ – сигнал с псевдослучайной перестройкой рабочей частоты |
|
|
|
10. ШС – шумовой сигнал |
|
|
Таблица 2. Спектральное представление сигналов на выходе КФУ
|
Класс сигналов |
Энергетический спектр |
Класс сигналов |
Энергетический спектр |
|
1. ГС |
|
6. ЛЧМС1 |
|
|
2. АМС |
|
7. ЛЧМС2 |
|
|
3. БМС |
|
8. ЛЧМС3 |
|
|
4. ЧМГ |
|
9. СППРЧ |
|
|
5. ФМС |
|
10. ШС |
|
Пояснения к табл.1 и 2:
![]() – амплитуда, частота и начальная
фаза сигнала;
– амплитуда, частота и начальная
фаза сигнала; ![]() – коэффициент передачи
размерностью
– коэффициент передачи
размерностью ![]() ;
; ![]() – временной сдвиг, вносимый ПЛЗ,
на i-м шаге перестройки
ПЛЗ;
– временной сдвиг, вносимый ПЛЗ,
на i-м шаге перестройки
ПЛЗ; ![]() – индексы
амплитудной и частотной модуляции;
– индексы
амплитудной и частотной модуляции; ![]() –
модулирующая частота;
–
модулирующая частота; ![]() – девиация частоты;
– девиация частоты; ![]() – манипулирующая
последовательность с длительностью элемента
– манипулирующая
последовательность с длительностью элемента ![]() , псевдослучайными коэффициентами
, псевдослучайными коэффициентами ![]() ;
; ![]() –
временное окно;
–
временное окно; ![]() – коэффициент корреляции сигнала
при
– коэффициент корреляции сигнала
при ![]() ;
; ![]() – псевдослучайная разность фаз;
– псевдослучайная разность фаз; ![]() – нижняя и верхняя границы ширины
спектра сигнала;
– нижняя и верхняя границы ширины
спектра сигнала; ![]() – скорость перестройки частоты и
длительность элемента ЛЧМС;
– скорость перестройки частоты и
длительность элемента ЛЧМС; ![]() – текущая частота, величина
частотного скачка и элемента СППРЧ;
– текущая частота, величина
частотного скачка и элемента СППРЧ; ![]() – длительность наблюдения за
сигналом;
– длительность наблюдения за
сигналом; ![]() – количество частот в
частотно-временной матрице СППРЧ;
– количество частот в
частотно-временной матрице СППРЧ; ![]() – средняя частота, ширина спектра
и фаза ШС;
– средняя частота, ширина спектра
и фаза ШС; ![]() – дисперсия, спектральная
плотность, коэффициент корреляции ШС;
– дисперсия, спектральная
плотность, коэффициент корреляции ШС; ![]() – разность текущих частот между
соседними элементами частотно-временной матрицы СППРЧ;
– разность текущих частот между
соседними элементами частотно-временной матрицы СППРЧ; ![]() – функция Бесселя нулевого и n-го
порядков.
– функция Бесселя нулевого и n-го
порядков.
После необходимых
преобразований в КФУ, сигнал подаётся на вход ПСА, состоящего из ![]() каналов, в которых осуществляется
фильтрация спектральных компонентов напряжения
каналов, в которых осуществляется
фильтрация спектральных компонентов напряжения ![]() и их линейное детектирование
согласно следующему соотношению:
и их линейное детектирование
согласно следующему соотношению:

где ![]() – напряжение на выходе канала ПСА
с частотой
– напряжение на выходе канала ПСА
с частотой ![]() ;
; ![]() – импульсная реакция k-ого
полосового фильтра с частотой
– импульсная реакция k-ого
полосового фильтра с частотой ![]() ;
; ![]() – ширина полосовых фильтров в
каналах ПСА;
– ширина полосовых фильтров в
каналах ПСА; ![]() – постоянная интегрирования на
выходе каналов ПСА.
– постоянная интегрирования на
выходе каналов ПСА.
Напряжения ![]() со всех каналов ПСА поступают в
РУ, где на каждом шаге перестройки ПЛЗ происходит обнаружение спектральных
компонентов напряжения
со всех каналов ПСА поступают в
РУ, где на каждом шаге перестройки ПЛЗ происходит обнаружение спектральных
компонентов напряжения ![]() , а также оценка их амплитуды и
частоты.
, а также оценка их амплитуды и
частоты.
Информация, полученная
в РУ, позволяет определить оптимальную величину задержки ![]() , которая с помощью Упр
устанавливается в ПЛЗ для осуществления классификации в режиме с фиксированной
настройкой ПЛЗ, что позволяет увеличить время накопления сигнала и, соответственно,
достоверность классификации.
, которая с помощью Упр
устанавливается в ПЛЗ для осуществления классификации в режиме с фиксированной
настройкой ПЛЗ, что позволяет увеличить время накопления сигнала и, соответственно,
достоверность классификации.
Величина полосы
пропускания и постоянная интегрирования в каналах ПСА выбираются из следующих
условий: ![]() а ширина рабочего частотного
диапазона ПСА выбирается из условия
а ширина рабочего частотного
диапазона ПСА выбирается из условия ![]() .
.
При приёме ГС алгоритм классификации имеет вид:
![]()
где ![]() – гипотеза о классификации ГС;
– гипотеза о классификации ГС; ![]() – напряжение на выходе канала ПСА
с
– напряжение на выходе канала ПСА
с ![]() ;
; ![]() – напряжение на выходе каналов ПСА
с
– напряжение на выходе каналов ПСА
с ![]() ;
; ![]() – пороговое напряжение.
– пороговое напряжение.
При приёме АМС алгоритм классификации имеет вид:
![]()
![]()
где ![]() – гипотеза о классификации АМС;
– гипотеза о классификации АМС; ![]() – напряжение на выходе каналов ПСА
с
– напряжение на выходе каналов ПСА
с ![]() и
и ![]() .
.
При приёме БМС алгоритм классификации имеет вид:
![]()
где ![]() – гипотеза о классификации БМС.
– гипотеза о классификации БМС.
При приёме ЧМГ алгоритм классификации имеет вид:
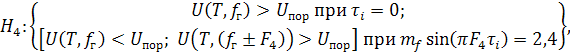
где ![]() – гипотеза о классификации ЧМС.
– гипотеза о классификации ЧМС.
При приёме ФМС алгоритм классификации имеет вид:
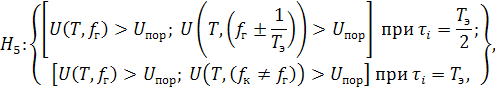
где ![]() – гипотеза о классификации ФМС;
– гипотеза о классификации ФМС; 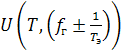 – напряжение на выходе каналов ПСА
с
– напряжение на выходе каналов ПСА
с ![]() .
.
При приёме ЛЧМС1 алгоритм классификации имеет вид:
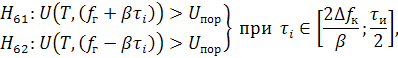
где ![]() – гипотеза о классификации ЛЧМС1
с нарастающим или спадающим законом изменения частоты;
– гипотеза о классификации ЛЧМС1
с нарастающим или спадающим законом изменения частоты; ![]() – набор напряжений на выходе
каналов ПСА при различных значениях
– набор напряжений на выходе
каналов ПСА при различных значениях ![]() .
.
При приёме ЛЧМС2 алгоритм классификации имеет вид:
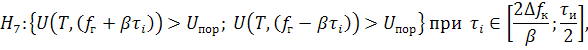
где ![]() – гипотеза о классификации ЛЧМС2.
– гипотеза о классификации ЛЧМС2.
При приёме ЛЧМС3 алгоритм классификации имеет вид:

где ![]() – гипотеза о классификации ЛЧМС3.
– гипотеза о классификации ЛЧМС3.
При приёме СППРЧ алгоритм классификации имеет вид:
![]()
где ![]() – гипотеза о классификации СППРЧ;
– гипотеза о классификации СППРЧ; ![]() – набор напряжений на выходах
каналов ПСА с частотами
– набор напряжений на выходах
каналов ПСА с частотами ![]() .
.
При приёме ШС алгоритм классификации имеет вид:
![]()
где ![]() – гипотеза о классификации ШС;
– гипотеза о классификации ШС; ![]() – интервал корреляции ШС.
– интервал корреляции ШС.
Достоверность
классификации сигналов зависит от таких характеристик, как отношения
сигнал/помеха на входе АКС ![]() , выходе КФУ
, выходе КФУ ![]() и выходе каналов ПСА
и выходе каналов ПСА ![]() ,
при которых обеспечивается допустимая вероятность ошибочной классификации
,
при которых обеспечивается допустимая вероятность ошибочной классификации ![]() .
.
Анализ достоверности классификации является предметом дальнейших исследований.
Для проверки результатов исследования и выполнения оптимизации параметров классификатора, воспользуемся программой системного проектирования SystemVue 6.0. Полученная функциональная схема КСС и параметры ФУ приводится на рис. 2.
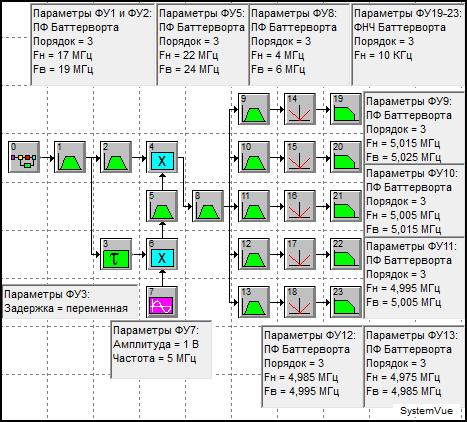
Рис. 2. Функциональная схема КСС
Функциональная схема на рис. 2 включает в себя:
ФУ 0 – метасистема, объединяющая генераторы связных сигналов; ФУ 1-8 – КФУ; ФУ 9-23 – 5-ти канальный ПСА.
В КФУ добавлен дополнительный ПФ (ФУ2) для компенсации задержки вносимой ПФ (ФУ5), а для упрощения процесса моделирования и уменьшения нагрузки на ЭВМ, количество каналов в ПСА уменьшено до пяти.
На рис. 3 изображена функциональная схема метасистемы, в которой представлены генераторы связных сигналов и параметры их ФУ.
Функциональная схема на рис. 3 включает в себя:
ФУ 0 – генератор ГС; ФУ 1-5 – генератор АМС; ФУ 6-8 – генератор БМС; ФУ 9,10 – генератор ЧМС; ФУ 11-13 генератор ФМС; ФУ 14-16 – генератор ЛЧМС1; ФУ 17-20 – генератор ЛЧМС2; ФУ 21-24 – генератор ЛЧМС3; ФУ 25,26 – генератор СППРЧ; ФУ 27,28 – генератор ШС; ФУ 30-39 – выходы метасистемы.
Моделирование обеспечивает проверку принципа действия КСС и оптимизацию параметров входящих в него функциональных узлов. Для каждого класса исследуемых сигналов обеспечивается снятие временных, спектральных и корреляционных характеристик процессов в контрольных точках на выходах ФУ и после анализа полученных результатов принимается решение о варьировании параметров с целью оптимизации функционирования КСС.
В данной работе для компактного представления результатов моделирования на рис. 4 приводятся эпюры спектральных распределений полезных эффектов на выходе каналов ПСА, реализованного в пятиканальном варианте, при различных значениях временного сдвига, вносимого линией задержки.
На основе анализа спектрограмм, приведённых на рис. 4, можно сделать следующие выводы.
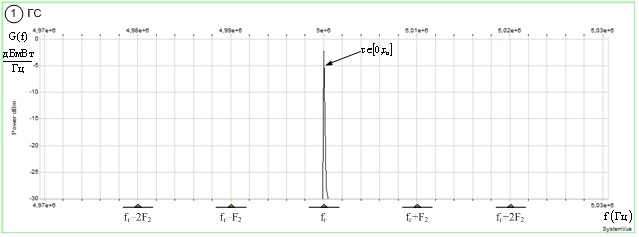
При классификации ГС
(рис. 4а) информативный признак представляет собой однокомпонентный процесс ![]() на частоте
на частоте ![]() , интенсивность которого инвариантна
к величине временного сдвига
, интенсивность которого инвариантна
к величине временного сдвига ![]() .
.

Рис. 3. Функциональная схема метасистемы
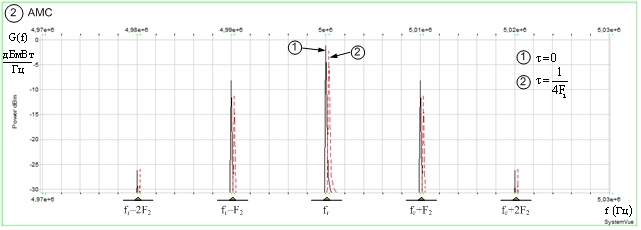
При классификации АМС
(рис. 4б) информативный признак представлен в виде пятикомпонентного процесса ![]() , причём интенсивность компонентов
, причём интенсивность компонентов ![]() ,
, ![]() ,
, ![]() ,
, ![]() инвариантна к величине временного
сдвига
инвариантна к величине временного
сдвига ![]() , а их уровень ниже интенсивности
компонента
, а их уровень ниже интенсивности
компонента ![]() не менее чем на 12 дБ при
не менее чем на 12 дБ при ![]() .
.
 а)
а)
 б)
б)
 в)
в)
 г)
г)
 д)
д)
 е)
е)
 ж)
ж)
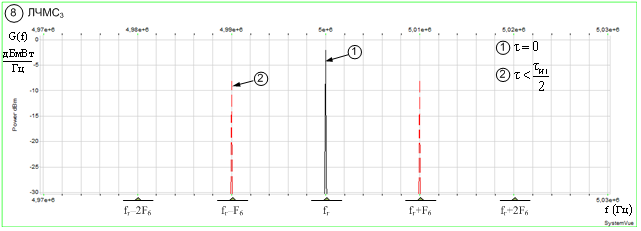 з)
з)
 и)
и)
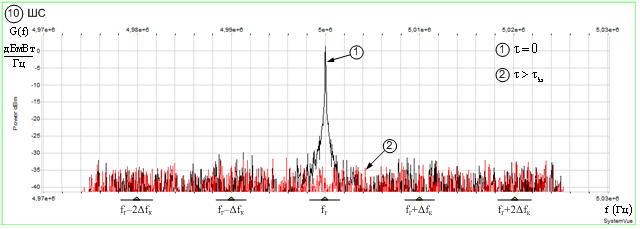 к)
к)
Рис. 4. Спектрограммы классифицируемых сигналов на выходе ПСА
При классификации БМС
(рис. 4в) состав и интенсивность информативного признака ![]() зависит от величины временного
сдвига
зависит от величины временного
сдвига ![]() . Так при
. Так при ![]() информативный признак является
трёхкомпонентным
информативный признак является
трёхкомпонентным ![]() , а при
, а при ![]() трансформируется в
двухкомпонентный
трансформируется в
двухкомпонентный ![]() и
и ![]() .
.
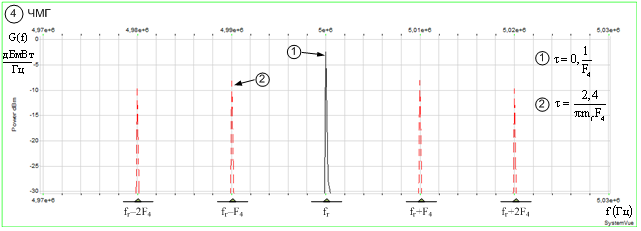
При классификации ЧМГ
(рис. 4г) состав и интенсивность информативного признака ![]() зависит от величины временного
сдвига
зависит от величины временного
сдвига ![]() . Так при
. Так при ![]() имеем
имеем ![]() , а при выполнении условия
, а при выполнении условия ![]() имеем компонент
имеем компонент ![]() , который состоит из спектральных
составляющих
, который состоит из спектральных
составляющих ![]() , интенсивность которых
неинвариантна к величине временного сдвига
, интенсивность которых
неинвариантна к величине временного сдвига ![]() .
.
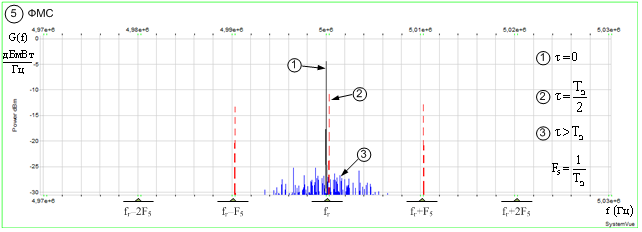
При классификации ФМС
(рис. 4д) состав и интенсивность информативного признака ![]() зависит от величины временного
сдвига
зависит от величины временного
сдвига ![]() . Так при
. Так при ![]() имеем
имеем ![]() , при
, при ![]() информативный признак становится
трёхкомпонентным
информативный признак становится
трёхкомпонентным ![]() , а при
, а при ![]() информативный признак представляет
собой компонент с непрерывным спектральным распределением
информативный признак представляет
собой компонент с непрерывным спектральным распределением ![]() .
.
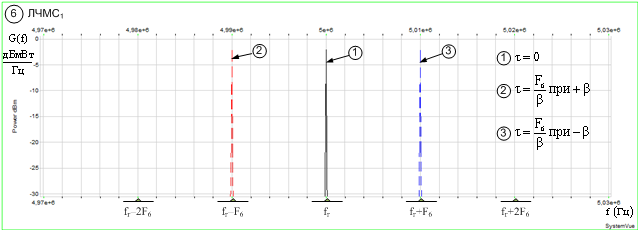
При классификации ЛЧМС1
(рис. 4е) информативный признак соответствует компоненту ![]() при нарастающей частоте сигнала, и
компоненту
при нарастающей частоте сигнала, и
компоненту ![]() при спадающей частоте, частотное
расположение которого зависит от величины временного сдвига
при спадающей частоте, частотное
расположение которого зависит от величины временного сдвига ![]() и знака
и знака ![]() .
.
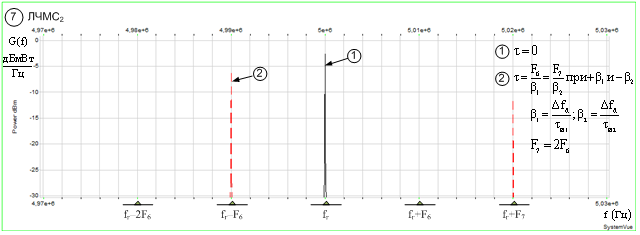
При классификации ЛЧМС2
(рис. 4ж) информативный признак является двухкомпонентным ![]() и
и ![]() при
при ![]() и
и ![]() , частотное расположение которых
несимметрично относительно
, частотное расположение которых
несимметрично относительно ![]() и зависит от величины
и зависит от величины ![]() ,
, ![]() и временного сдвига
и временного сдвига ![]() .
.
При классификации ЛЧМС3
(рис. 4з) состав и интенсивность информативного признака зависит от величины
временного сдвига ![]() . Так при
. Так при ![]() имеем
имеем ![]() , а при
, а при ![]() информативный признак становится
двухкомпонентным
информативный признак становится
двухкомпонентным ![]() и
и ![]() , составляющие которого симметрично
расположены относительно
, составляющие которого симметрично
расположены относительно ![]() , а величина
, а величина ![]() неинвариантна, относительно
временного сдвига
неинвариантна, относительно
временного сдвига ![]() .
.
При классификации СППРЧ
(рис. 4и) состав и интенсивность информативного признака зависит от величины
временного сдвига ![]() . Так при
. Так при ![]() имеем
имеем ![]() , а при
, а при ![]() имеем
имеем ![]() при
при ![]() ,
, ![]() . При времени наблюдения
. При времени наблюдения ![]() информативный признак состоит из
информативный признак состоит из ![]() компонент
с различными частотами
компонент
с различными частотами ![]() .
.
При классификации ШС
(рис. 4к) состав и интенсивность информативного признака зависит от величины
временного сдвига ![]() . Так при
. Так при ![]() имеем
имеем ![]() , при этом компонент
, при этом компонент ![]() превосходит по интенсивности
компоненты
превосходит по интенсивности
компоненты ![]() пропорционально коэффициенту
фильтрации
пропорционально коэффициенту
фильтрации ![]() , где
, где ![]() – ширина спектра ШС,
– ширина спектра ШС, ![]() –
постоянная интегрирования в ПСА. При
–
постоянная интегрирования в ПСА. При ![]() , где
, где ![]() – интервал корреляции ШС, имеем
компонент
– интервал корреляции ШС, имеем
компонент ![]() , который имеет непрерывное
распределение, причём интенсивность
, который имеет непрерывное
распределение, причём интенсивность ![]() меньше интенсивности
меньше интенсивности ![]() пропорционально
пропорционально ![]() .
.
Результаты моделирования подтверждают теоретические исследования.
Материалы данной работы могут быть использованы при проектировании автоматических многофункциональных комплексов радиомониторинга.
Литература
1. Афонский А.А., Дьяконов В.П. Цифровые анализаторы спектра, сигналов и логики. – М.: Солон-Пресс; 2009. – 248 с.
2. Патент РФ №2353050. Адаптивное многофункциональное корреляционно-фильтровое устройство. БИ №11, 2009