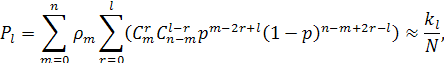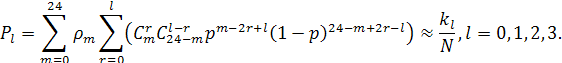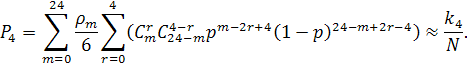УДК 621.391
ОЦЕНКА ВЕРОЯТНОСТИ ОШИБКИ НА БИТ ПО РЕЗУЛЬТАТАМ ДЕКОДИРОВАНИЯ КОДОВЫХ СЛОВ
В. В. Егоров, М. С. Смаль
ОАО «Российский институт мощного радиостроения, Санкт-Петербург
Статья получена 1 апреля 2013 г.
Аннотация. Рассмотрен способ оценки вероятности ошибки на бит в канале связи на основе анализа результатов декодирования кодовых слов линейных блоковых кодов, показана возможность их использования для систем передачи данных на примере расширенного кода Голея (24,12,8).
Ключевые слова: вероятность ошибки на бит, канал связи, помехоустойчивое кодирование, передача данных.
Abstract: Method of bit error probability estimation via decoder results analysis for linear block codes is reviewed in the article. Possibility of its application for data communications by the example of Golay code (24,12,8) is shown.
Key words: bit error probability, communication channel, error correction code, data communications.
При передаче данных по нестационарному радиоканалу связи неизбежны ошибки в принимаемых символах сообщений. Поэтому для безошибочной передачи или уменьшения их количества до допустимого значения используют помехоустойчивое кодирование. При этом, чаще всего на приемной стороне известна схема, с помощью которой было закодировано исходное сообщение. Корректирующая способность помехоустойчивого кода определяется его избыточностью. Очевидно, что в нестационарных радиоканалах априорно невозможно задать оптимальные параметры кода, обеспечивающие максимальную кодовую скорость при заданной достоверности. Поэтому получили широкое распространение адаптивные системы передачи данных, в которых параметры кода изменяются в зависимости от состояния канала связи. Исходными данными для целенаправленного изменения параметров кода является вероятность ошибки на бит.
В большинстве существующих на сегодняшний день систем передачи данных оценка вероятности ошибки на бит осуществляется путём периодической посылки тестовой последовательности, известной на приёмной стороне, и подсчете количества искаженных бит. Очевидным недостатком такого подхода является необходимость прерывания информационного потока, что приводит к значительному снижению информационной скорости.
Поэтому актуальной для таких систем является задача разработки методов оценки вероятности ошибки на бит непосредственно по результатам декодирования кодовых слов. При этом, воспользоваться прямым подсчётом количества обнаруженных кодом ошибок не удаётся, так как количество обнаруженных ошибок в неверно декодированных кодом словах будет больше, чем вычислено в результате синдромного декодирования. Полученная таким образом оценка является заведомо заниженной, что приводит к выбору параметров кода, который может не обеспечить требуемую достоверность.
Будем считать, что применяется линейный блоковый код с
параметрами 
и для его декодирования используется
алгоритм вычисления синдрома, указывающего позиции и количество обнаруженных
кодом ошибок. Тогда вероятность события, когда при декодировании принятого
кодового слова длиной 
синдром обнаружит 
ошибок, определяется выражением:
|
|
(1) |
где 
количество кодовых слов веса 
, 
вероятность ошибки на бит, 
подсчитанное количество произошедших указанных
событий.
Данное выражение получено из следующих соображений.
Рассмотрим вероятность события, состоящего в том, что при декодировании
принятого кодового слова длиной код обнаружит одну ошибку. Данное
событие произойдет, если в слове произошла действительно 1 ошибка, либо
принятое слово находится на расстоянии 1 по Хэммингу от любого другого
разрешенного слова. Если принятое слово находится на расстоянии 1 от ложного
слова (расстояние между ложным и истинным словом при этом равно ), то это значит, что в принятом слове может быть либо
, либо 
ошибка. Аналогичные выводы можно
сделать и для случаев, когда произошло более 1 ошибки.
В общем случае данные вероятности не составляют полную группу событий, поскольку часть принятых кодовых слов могут находиться вне сферы Хэмминга. Поэтому данные зависимости являются справедливыми при выполнении следующего условия:
|
|
(2) |
Будем считать, что количество принятых кодовых слов 
достаточно велико. В этом случае имеется возможность
определить частости таких событий 
, которые будут являться несмещёнными
оценками соответствующих вероятностей 
. Таким образом, удаётся установить
аналитическую связь между искомой вероятностью ошибки на бит и доступной для
измерения оценки вероятности соответствующих событий.
Для примера рассмотрим расширенный код Голея (24,12,8), широко используемый как внутренний код каскадных кодовых конструкций.
Порождающий полином данного кода имеет следующий вид [1]:
|
|
(3) |
Код обладает следующим спектром, отличные от нуля компоненты которого приведены в таблице 1.
Таблица 1. Распределение весов кодовых слов кода Голея (24,12,8)
|
Вес слова |
0 |
8 |
12 |
16 |
24 |
|
Число слов |
1 |
759 |
2576 |
759 |
1 |
В этом случае вероятности событий, когда при декодировании
принятого кодового слова длиной 24, код обнаружит 0, 1, 2 или 3 ошибки, если
вероятность ошибки в канале связи равна 
, определяются выражениями:
|
|
(4) |
При этом, выражение для 
имеет другой вид, так как 
не удовлетворяет условию (2). В этом
случае в данном выражении возникает множитель 
, который объясняется особенностью
структуры расширенного кода Голея, заключающейся в том, что от любого стертого
символа на расстоянии 4 находятся 6 разрешённых кодовых слов:
|
|
(5) |
Данные вероятности составляют полную группу событий, т.е. выполняются равенства:
|
|
(6)
|
Рисунок 1. Зависимости вероятностей обнаружения кодом ошибок от вероятности ошибки на бит в канале связи.
На рисунке 1 изображены зависимости соответствующих
вероятностей
от вероятности ошибки на бит в
канале связи, из которого видно, что в интересующей области, когда вероятность
ошибки на бит менее 0,2, указанные вероятности значительно меняются. Таким
образом, приняв кодовый блок из кодовых слов, в которых могут
содержаться ошибки, после операции декодирования можно вычислить необходимые
значения 
и соответствующие частости и
составить систему нелинейных уравнений, в которой единственной неизвестной
величиной будет являться искомая вероятность ошибки на бит 
в канале связи. При этом, абсолютно неважно,
правильно ли произошло декодирование, т.е. в словах может быть более 4 ошибок и
после декодирования решение может быть вынесено в пользу неверного
информационного слова.
Для решения полученной системы нелинейных уравнений можно
использовать подход, который состоит в том, чтобы найти решение каждого
уравнения, а затем их совместно обработать. Стоит отметить, что данная система
уравнений является переопределенной. Однако при этом необходимо учитывать
следующую особенность данной системы. В правой части данной системы уравнений
находятся частости событий , которые могут принимать случайные
значения. Если в кодовом блоке, содержащем кодовых слов, вычисленная частость 
оказалась больше максимально
возможной, соответствующей 
, то полученное уравнение для данной
частости не будет иметь решения. Тогда, если искать решения в каждом уравнении
отдельно, то перед тем как начинать поиск, нужно отбросить уравнения, не
имеющие решения. Получив решения, их необходимо совместно обработать и найти
конечную оценку вероятности ошибки на бит. Таким образом, суть данного подхода
состоит в том, что искомая оценка является решением данной системы уравнений.
Второй подход, который можно применить, является вероятностным. Суть подхода состоит в том, что в каждом конкретном опыте для заданной вероятности ошибки на бит может быть получен вектор частостей, являющийся оценкой вектора соответствующих вероятностей. В этом случае можно применить методы, которые используются для определения меры близости плотностей или функций распределения. Тогда искомая оценка вероятности ошибки на бит выбирается из условия минимума расстояния между эмпирическим и теоретическим распределениями, широко используемого в задачах математической статистики [2].
Таким образом, используя данный способ, можно оценить текущее значение вероятности ошибки на бит вне зависимости от количества ошибок и факта декодирования кодовых слов, а также не прерывая поток полезной информации. При этом, использование тестовых сигналов или введение дополнительной избыточности для этого не требуется, что позволяет максимально эффективно использовать время передачи и повысить информационную скорость. Получение оценки возможно непрерывным скользящим окном, размер которого выбирается из конкретных условий использования.
1. Морелос-сарагоса Р. Искусство помехоустойчивого кодирования. Методы, алгоритмы, применение. — М. : Техносфера, 2005.
2. Кокс Д., Хинкли Д. Теориетическая статистика. — М. : Мир, 1978.