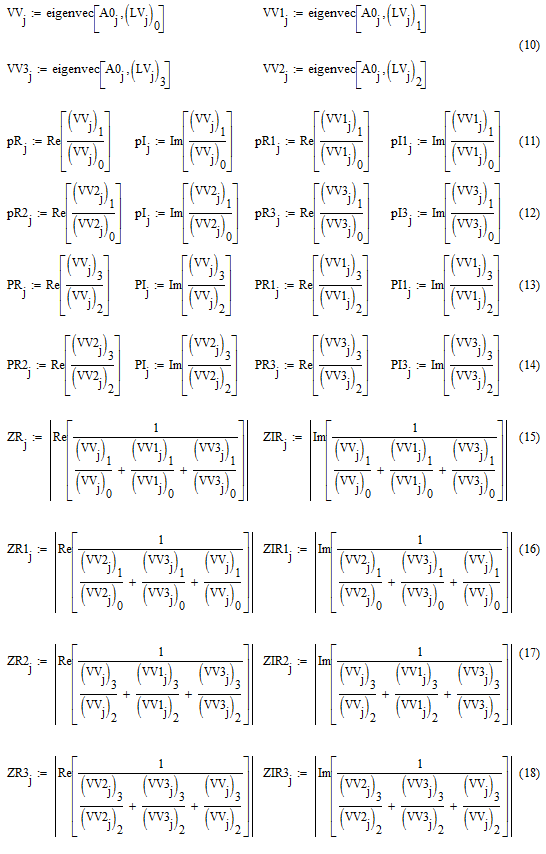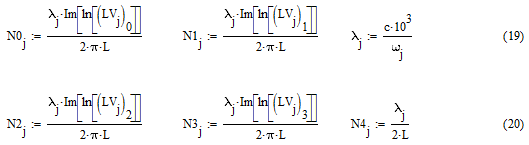Анализ дисперсионных характеристик замедляющих систем с пролетным каналом, заполненным плазмой, методом трехмерного моделирования
Н. П. Кравченко, С. В. Мухин
Национальный исследовательский университет "Высшая школа экономики"
Статья получена 14 апреля 2014 г.
Аннотация. Целью настоящей работы является разработка алгоритма и программы расчета дисперсионных характеристик резонаторных замедляющих систем с пролетным каналом, заполненным плазмой, с использованием методов трехмерного моделирования. Для достижения поставленной цели в работе были решены следующие задачи:
1. сформулирована задача описания ячейки резонаторной замедляющей системы с пролетным каналом, заполненным плазмой, матрицей передачи многополюсника и приведены соотношения для определения электродинамических характеристик замедляющих систем через коэффициенты этой матрицы;
2. дан обзор методов решения ключевых задач электродинамики и программ, пригодных для определения коэффициентов матрицы передачи многополюсника, моделирующего ячейку замедляющей системы;
3. разработан алгоритм и программа обработки данных трехмерного моделирования резонаторной замедляющей системы;
4. проведен анализ дисперсионных характеристик резонаторных замедляющих систем при изменении концентрации плазмы.
Ключевые слова: замедляющая система, многополюсник, трехмерное моделирование, электродинамические характеристики.
Abstract. The aim of this work is to develop an
algorithm and program for calculating the dispersion characteristics of the
resonator slow-wave systems with channel -flight filled with plasma, using the
methods of three-dimensional modeling.
To achieve this
goal the following problems were solved:
1. the problem of describing the cell resonator slow-wave system with
channel-flight filled with plasma transfer multipole matrix is formed and the
ratio for determination the dynamic characteristics of slow-wave systems of the
coefficients of the matrix are shown;
2. a review of methods for solving key problems of electrodynamics and programs
suitable for determining the coefficients of the transfer matrix multipole
modeling cell slow-wave system are given;
3. algorithm and data processing of software simulation of three-dimensional resonator slow-wave system are developed;
4. an analysis of the dispersion characteristics of the resonator slow-wave systems when the concentration of plasma is fulfilled.
Keywords: slow-wave structure, multipole, three-dimensional modeling, electrodynamic characteristics.
1. Введение.
В последние годы наблюдается быстрое расширение области применения электромагнитных полей микроволнового диапазона, что стимулирует появление новых типов микроволновых устройств, развитие компьютерных методов их расчета и проектирования. В свою очередь, появление новых микроволновых генераторов, усилителей, преобразователей, разработка новых материалов, линий передачи, фильтров и других устройств позволяет продвигать микроволновые технологии в новые области науки и техники.
Для описания ламп с бегущей волной (ЛБВ) с дискретным взаимодействием, в которых фаза поля в зазорах взаимодействия в продольном направлении остается постоянной, электродинамически обоснованным является использование разностного уравнения для напряжений V на зазорах
где Aij - коэффициенты матрицы передачи.
Этому уравнению соответствует шестиполюсник, у которого входы возбуждения полем и током объединены. Секция ЛБВ, возбуждаемая заданным током, в этом случае моделируется цепочкой таких шестиполюсников (рис.1.1), что позволяет легко учитывать граничные условия на концах секции и отражения, возникающие при объединении в секцию неидентичных ячеек.

Рис.1.1. Модель секции ЛБВ, составленная из шестиполюсников.
Адекватность математической модели дискретного взаимодействия определяется точностью задания коэффициентов конечно–разностного уравнения, имеющих определенный электродинамический смысл и определяемых через коэффициенты матрицы передачи четырехполюсника, который получается из шестиполюсника в отсутствии возбуждающего тока. Этот четырехполюсник, в свою очередь, является математической моделью ячейки резонаторной замедляющей системы (ЗС). Коэффициенты четырехполюсника определяют точность восстановления электродинамических характеристик моделируемой резонаторной замедляющей системы. Таким образом, их правильный выбор обеспечивает одновременно адекватное описание процессов дискретного взаимодействия в ЛБВ и электродинамических процессов в замедляющей системе.
Поэтому разработка простых и точных моделей резонаторных ЗС, используемых при моделировании приборов, является актуальной задачей.
Целью настоящей работы является разработка алгоритма и программы расчета дисперсионных характеристик резонаторных замедляющих систем с пролетным каналом, заполненным плазмой, с использованием результатов их трехмерного моделирования.
2. Представление ячейки резонаторной замедляющей системы многополюсником.
Цельнометаллическая
резонаторная замедляющая система представляет собой линию передачи, созданную объединением
в цепочку ячеек с идентичной структурой. Ячейки соединяются друг с другом
волноведущими каналами, которые можно разделить на входные в сечении Sa1, a=1,2,....k и
выходные в сечении Sa2,
a=1,2,...![]() . Поскольку ЗС периодична, расстояние между
входным Sa1 и выходным Sa2 сечениями ячейки равно периоду D замедляющей системы, при этом число входных каналов всегда
равно числу выходных каналов (k=l=N).
. Поскольку ЗС периодична, расстояние между
входным Sa1 и выходным Sa2 сечениями ячейки равно периоду D замедляющей системы, при этом число входных каналов всегда
равно числу выходных каналов (k=l=N).
Полные тангенциальные поля Еat(x,y,z) и Hat(x,y,z) во входных и выходных сечениях Sa1(2) представляют собой суперпозицию бесконечного числа типов волн, которые свойственны соответствующему волноведущему каналу.
Согласно [1] имеем:
![]() ,
,
где ![]() ,
,![]() - известные векторные функции распределения
электрического и магнитного полей для n-го типа волны в поперечном сечении
канала, зависящие от поперечных координат x,y; n(a) - номер собственной волны в канале с номером a;
- известные векторные функции распределения
электрического и магнитного полей для n-го типа волны в поперечном сечении
канала, зависящие от поперечных координат x,y; n(a) - номер собственной волны в канале с номером a;
![]() - комплексные амплитуды функций поперечных
векторов, которые включают в себя зависимость от продольной координаты z. Будем
учитывать конечное число членов в разложениях (2.1). В каждом канале в сечении
Sa суммируются N собственных волн
(n=1,2,....N).
- комплексные амплитуды функций поперечных
векторов, которые включают в себя зависимость от продольной координаты z. Будем
учитывать конечное число членов в разложениях (2.1). В каждом канале в сечении
Sa суммируются N собственных волн
(n=1,2,....N).
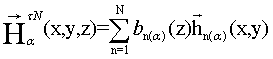
Поскольку ячейка
замедляющей системы является пассивным линейным объектом, комплексные амплитуды
![]() на ее входе и выходе связаны
линейным оператором [2], определяемым матрицей передачи AN.
на ее входе и выходе связаны
линейным оператором [2], определяемым матрицей передачи AN.
Связь между компонентами полей на обеих границах Sa1,2 задаётся в виде
где ![]() ,
, ![]() - векторы, составленные из комплексных амплитуд в
сечениях Sa1,2.
- векторы, составленные из комплексных амплитуд в
сечениях Sa1,2.
АN - матричный линейный оператор вида
Если элементы матричного оператора AN известны, замедляющая система полностью формализована, и можно определить все ее электродинамические характеристики.
Тангенциальные составляющие поля в сечениях Sa1(2), задаваемые выражением (2.2) , полностью определяют поле нормальной волны во всем объеме ячейки. В сечениях Sa1 и Sa2 они связаны условиями Флоке [3]:
![]() ,
,
где hn - постоянная распространения n-ой нормальной волны в ячейке с периодом D. Условие (2.5) с учетом (2.3) записывается относительно векторов комплексных амплитуд как
Из (2.6) с учетом (2.3),
исключив ![]() и
и ![]() , получим
, получим
Выражение (2.7) является алгебраической формулировкой задачи о собственных волнах исследуемой замедляющей системы при представлении ее ячейки 2N-полюсником, который описывается линейным матричным оператором AN .
Нетривиальное решение системы уравнений (2.7) существует, если выполняется условие [4]
где ![]() - собственные числа матрицы передачи AN, дающие возможность определять
постоянные распространения hn 2N-полюсника, моделирующего ячейку ЗС; Е - единичная матрица.
- собственные числа матрицы передачи AN, дающие возможность определять
постоянные распространения hn 2N-полюсника, моделирующего ячейку ЗС; Е - единичная матрица.
Согласно [4], выражение (2.8) является дисперсионным уравнением нормальных волн 2N-полюсника. Дисперсионное уравнение вида j=f(w) получается из (2.8), поскольку элементы матричного оператора AN зависят от частоты w.
Собственные векторы матрицы передачи AN вместе с выражением (2.2) определяют поперечные электромагнитные поля, отвечающие собственным волнам в 2N-полюснике, моделирующем ячейку замедляющей системы, и могут быть использованы для определения характеристического сопротивления линии передачи.
Таким образом, электродинамические характеристики замедляющей системы могут быть определены, если известны элементы матрицы передачи AN , полученной в результате формализации ячейки.
В настоящей работе на основе разработанных программ обработки результатов трехмерного моделирования замедляющих систем проведен анализ дисперсионных характеристик и гибридных замедляющих систем с пролетным каналом, заполненным плазмой.
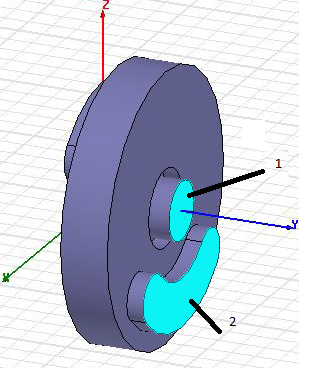
Для исследования плазменного заполнения пролетного канала рассматривались замедляющие системы с прямоугольным и аксиально-симметричным сечением, разрезанные по щелям связи.
Эти модели имеют четыре порта и моделируются восьмиполюсниками. Пролетный канал заполнен плазмой без столкновений. Если пренебречь тепловыми скоростями электронов, то свойства плазмы описываются с помощью диэлектрического тензора
 ,
,
где 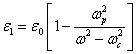 ,
,  ,
, 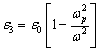 ,
, ![]() – циклотронная частота,
– циклотронная частота, 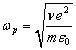 – плазменная частота,
– плазменная частота, ![]() – концентрация плазмы,
– концентрация плазмы, ![]() – магнитное поле. В ISFELD 3D для создания материала плазмы требовалось
вручную вводить зависимость плазменной частоты от частоты электромагнитной
волны.
– магнитное поле. В ISFELD 3D для создания материала плазмы требовалось
вручную вводить зависимость плазменной частоты от частоты электромагнитной
волны.
Элементы матрицы передачи можно определить с помощью трехмерного моделирования. Результат расчета представляет собой S-матрицу или эквивалентные ей Y и Z-матрицы. С помощью формул перехода можно преобразовать S и Z-матрицы в А-матрицу и рассчитать электродинамические характеристики.
3. Методы определения элементов матричного оператора 2N-полюсника, описывающего характеристики замедляющей системы.
Метод конечных элементов (МКЭ) является одним из наиболее мощных и универсальных инструментов численного решения уравнений математической физики. Этот метод может быть использован для решения электродинамических задач как во временной, так и в частотной областях.
Метод основан на разбиении расчетной области на большое количество подобластей – конечных элементов (КЭ) и представления поля в каждом из них в виде разложения по некоторой системе линейно независимых финитных функций, отличных от нуля только внутри данного элемента. Форма КЭ может быть различной, однако, она должна обеспечивать плотное покрытие области набором КЭ без наложений и зазоров. Этим требованиям удовлетворяют, в частности, КЭ в форме тетраэдров, гексаэдров и октаэдров, а так же призм. Конечно-элементарная сетка, которой покрывается расчетная область, может быть нерегулярной и сгущаться в тех местах, где ожидается наиболее быстрое изменение поля.
В качестве функций, используемых для аппроксимации поля в КЭ, обычно используют полиномиальные функции координат различного порядка, построенные таким образом, чтобы коэффициенты разложения поля были равны значениям этого поля в вершинах КЭ или на его ребрах. Применение вариационного метода позволяет получить систему уравнений относительно этих коэффициентов, решив которую, можно получить искомые значения напряженности или потенциала в узлах или на ребрах и тем самым приближенно восстановить поле во всей области.
Сравнительная сложность алгоритма и большой объем памяти, требуемый для решения задачи методом МКЭ, компенсируется возможностью достаточно точной аппроксимации границ моделирования полей в областях, заполненных неоднородными и анизотропными средами, а также малым временем решения задачи. Существует множество модификаций данного метода и поэтому имеется возможность выбрать его оптимальную реализацию для решения конкретного класса задач.
Анализ доступности программных продуктов и их возможностей позволил остановить выбор на программе ISFELD 3D.
Для расчета методом Driven Modal достаточно смоделировать одну ячейку периодической системы, кроме того, требуется задать входные и выходные порты. Следует отметить, что этот метод является универсальным и используется не только для расчета замедляющих систем. Номера портов и геометрические размеры ячейки изображены на рис.3.1.
Рис.3.1. Ячейка замедляющей системы, разрезанная по щелям связи . Цветом выделены порты.
Портом обозначается место соединения трехмерной модели с бесконечным волноводом, через который поступает входной сигнал или выходит выходной. Кроме портов, нам требуется задать диапазон частот, в котором будет производиться расчет системы, а также шаг, с которым будет меняться расчетная частота внутри диапазона. После того, как все эти условия заданы, происходит расчет системы подобно методу Eigenmode, с той лишь разницей, что после разбиения на тетраэдры расчет производится отдельно для каждой частоты из заданного диапазона. В результате мы получим матрицу рассеяния S и эквивалентные ей Z и Y-матрицы. Эти данные будут использованы для расчета дисперсионных характеристик ЗС.
При рассмотрении замедляющих систем с пролетным каналом, заполненным плазмой, пролетный канал моделируется материалом, соответствующим плазме.
4. Программа обработки данных трехмерного моделирования.
В работе рассматриваются резонаторные замедляющие системы представляемые четырехполюсниками и восьмиполюсниками. Данные замедляющие системы, моделируются в ISFELD 3D ячейками с двумя и четырьмя портами соответственно.
В качестве исходных данных могут быть использованы наборы S, Z и T матриц, полученных для заданного в ISFELD 3D набора частот.
S-Матрица рассеяния — матрица, элементы которой описывают физические параметры рассеяния. В технике СВЧ матрица рассеяния связывает линейной зависимостью падающую и отражённую волны на входах многополюсника.
Впервые матрица рассеяния была введена Джоном Уилером в работе 1937 года. В этой работе Уилер ввел понятие матрицы рассеяния — унитарной матрицы коэффициентов, которые связывают "асимптотическое поведение произвольного частичного решения [интегрального уравнения] с решениями в стандартной форме".
Каждый вход описываемого многополюсника в технике СВЧ принято представлять в виде линии передачи с основным типом волн. Следовательно, на каждом входе многополюсника существуют как падающая a, так и отражённая b волны. Отраженные волны связаны с падающими линейными зависимостями.
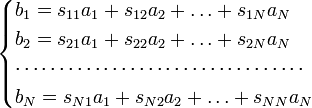
Если представить падающие и отражённые волны на входах многополюсника в виде векторов a и b:
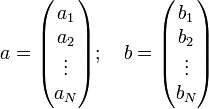
В этом случае линейные зависимости, указанные выше, можно записать в матричной форме
![]()
Здесь S - матрица рассеяния.

Чтобы определить физический смысл элементов матрицы, необходимо на вход n подать падающую волну, а ко всем остальным входам подключить согласованную не отражающую нагрузку
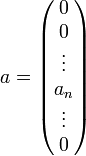
Тогда ![]() ,
откуда
,
откуда ![]() .
.
Таким образом, элементы матрицы рассеяния представляют собой коэффициенты передачи со входа n на вход m, при n=m и коэффициенты отражения, если n=m (главная диагональ).
Следует отметить особое положение матрицы рассеяния среди других матриц четырехполюсников и многополюсников. Действительно, в ней все коэффициенты имеют простой физический смысл и связанны непосредственно с рабочим режимом четырехполюсника. При изменении направления передачи в матрице S меняются соответственно только индексы (S12 → S21, S11 → S22), но не происходит (как это имеет место в других типах матриц) изменения величины и знаков элементов. Таким образом матрица S фактически не связанна с каким-либо заданным направлением передачи; это весьма удобно при решении ряда задач на СВЧ, в частности – в случае многополюсников, соединенных произвольным образом.
T-матрица это ненормированная волновая матрица передачи. Коэффициенты Т11 и Т21, определяют свойства четырехполюсника, нагруженного на согласованную линию при прямом направлении передачи. Коэффициент Т11 определяет отношение нормированных напряжений и называется коэффициентом передачи. Коэффициент Т21 связывает отраженную волну во входной цепи с падающей волной в выходной цепи.
Алгоритм обработки данных трехмерного моделирования включает:
1. Ввод исходных данных из файла.
2. Преобразование исходной S, Z или T матрицы в A матрицу.
3. Определение собственных чисел A матрицы.
4. Определение собственных векторов A матрицы.
5. Расчет замедления и характеристического сопротивления ЗС.
6. Представление графических материалов.
В качестве программной среды используется MathCAD. Данный математический пакет обладает всеми необходимыми функциями для решения поставленной нами задачи, а именно: считывание данных из файлов, операции с матрицами, расчет собственных значений и векторов матриц, построение графиков.
Были разработаны две программы для модели ячейки замедляющей системы с двумя портами и модели ячейки с четырьмя портами, что соответствует исключению из рассмотрения пролетного канала и его учет.
Модель с четырьмя портами.
Рассмотрим программу, которая описывает замедляющую систему, представленную в виде восьмиполюсника. Листинг программы представлен ниже. Аналогично предыдущему случаю, используем для считывания содержимого этого файла в MathCAD команду вида:
![]() .
.
Задается так же период системы и количество частот, для которых ведется расчет. Период определяется продольным размером моделируемой ячейки L. Количество частот определяется величиной шага, с которым изменяется расчетная частота в программе ISFELD 3D. Данное значение мы задаем в MathCAD как количество шагов N.
Из считанной из файла таблицы выбирается набор частот и набор матриц Z, которые соответствуют этим частотам. С этой целью используем следующие команды (1), (2) и (3).
Соответственно ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() элементы
j-ой Z-матрицы, а ωj – расчетная частота. Для преобразования Z-матриц в эквивалентные A-матрицы используется матрица
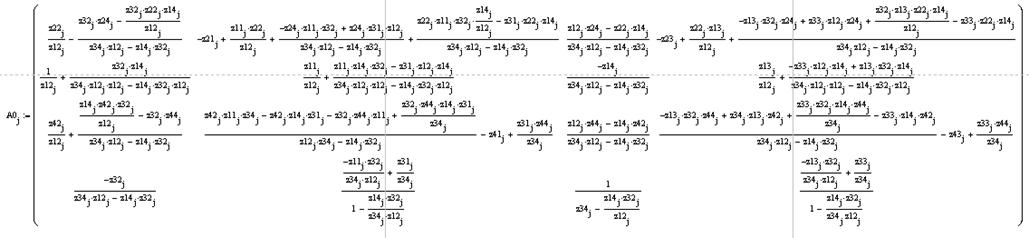
перехода (4), однако, в отличие от предыдущего случая, матрица имеет
размерность 4х4. Из-за больших размеров этой матрицы она показана на рис.4.1.
элементы
j-ой Z-матрицы, а ωj – расчетная частота. Для преобразования Z-матриц в эквивалентные A-матрицы используется матрица
перехода (4), однако, в отличие от предыдущего случая, матрица имеет
размерность 4х4. Из-за больших размеров этой матрицы она показана на рис.4.1.
После получения нужной нам А-матрицы мы можем рассчитать ее собственные значения, используя функцию (5).
Собственные значения являются комплексными числами. В данном случае A-матрица имеет размерность 4х4, в результате чего мы получаем четыре собственных значения, причем они будут попарно комплексно сопряженными. Для получения значений фазы и реактивного затухания используем формулы (6), (7), (8), (9). Собственные числа сопряжены соответственно первое с четвертым и второе с третьим (0-3, 1-2). Каждая пара собственных чисел соответствует «каналу» распространения волны в ячейке. Канал образуется каждой парой портов, которые заданы при моделировании (рис. 3.1). Таким образом, мы получим две кривых набега фазы на ячейку и две кривых реактивного затухания, по одной на каждый канал. То же самое будет и с другими параметрами.
Для расчета характеристического сопротивления рассчитываются собственные векторы (10). Четырем собственным значениям матрицы соответствуют четыре собственных вектора, которые могут быть использованы для определения характеристических сопротивлений модели.
Действительные и мнимые части характеристических сопротивлений мод зазора взаимодействия вычисляются по формулам (11), (12), пролетного канала – (13), (14).
При расчете возбуждения
ячейки заданным током целесообразно рассматривать полное характеристическое
сопротивление, которое можно рассчитать по формулам (15), (16), (17), (18). ![]() – действительная и мнимая часть полного
характеристического сопротивления прямой волны зазора взаимодействия,
– действительная и мнимая часть полного
характеристического сопротивления прямой волны зазора взаимодействия, ![]() – действительная и мнимая часть полного
характеристического сопротивления обратной волны зазора взаимодействия,
– действительная и мнимая часть полного
характеристического сопротивления обратной волны зазора взаимодействия, ![]() – действительная и мнимая часть полного
характеристического сопротивления прямой волны пролетного канала,
– действительная и мнимая часть полного
характеристического сопротивления прямой волны пролетного канала, ![]() – действительная и мнимая часть
характеристического сопротивления обратной волны пролетного канала.
– действительная и мнимая часть
характеристического сопротивления обратной волны пролетного канала.
Следующий этап расчета – получение коэффициента замедления (19), (20). Для этого требуется взять произведение фазы и длины волны, поделенное на 2πL, где L – период системы.
5. Анализ влияния плазмы на дисперсионные характеристики.
Одним из направлений исследований в области сверхвысоких частот (СВЧ) является создание приборов на основе гибридных замедляющих cистем с пролетным каналом, заполненным плазмой [5,6]. В разные годы разными научными группами были проведены исследования, включающие теоретический анализ пучково-плазменных процессов, экспериментальные исследования нерелятивистских генераторов на плазменных лампах обратной волны, а также созданы образцы пучково-плазменных ЛБВ.
Несмотря на большой объем проведенных теоретических и экспериментальных исследований замедляющих систем с пролетным каналом, заполненным плазмой, и процессов взаимодействия электронных потоков с волнами в таких системах, до настоящего времени нет инструмента, позволяющего вести машинное моделирование процессов взаимодействия, происходящих в пучково-плазменных приборах.
В настоящей работе на основе разработанных программ обработки результатов трехмерного моделирования замедляющих систем проведен анализ дисперсионных характеристик и гибридных замедляющих систем с пролетным каналом, заполненным плазмой.
В используемой программе
трехмерного моделирования возможно задание только ненамагниченной плазмы, для
которой ![]() и
и ![]() . Это не полностью отражает физические
процессы в реальной ЛБВ, однако, позволяет сравнить полученные результаты с
натурным экспериментом и оценить влияние плазмы на дисперсионные характеристики
замедляющей системы. При моделировании пролетного канала заполняющий его
материал имеет диэлектрическую проницаемость плазмы
. Это не полностью отражает физические
процессы в реальной ЛБВ, однако, позволяет сравнить полученные результаты с
натурным экспериментом и оценить влияние плазмы на дисперсионные характеристики
замедляющей системы. При моделировании пролетного канала заполняющий его
материал имеет диэлектрическую проницаемость плазмы ![]() .
.
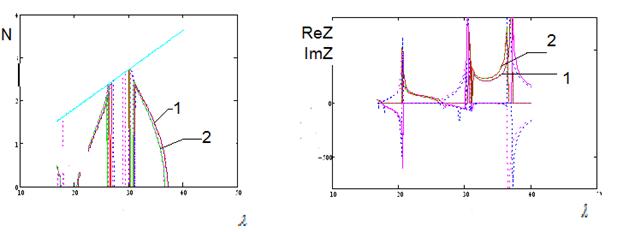
На рис. 5.1, 5.2
представлены результаты расчета дисперсионных характеристик прямоугольных ЦСР с
разной высотой щелей связи (1.3мм и 4.3мм, соответственно) при концентрации
плазмы ![]() в сравнении с дисперсионными характеристиками прямоугольной
ЦСР без плазменного заполнения.
в сравнении с дисперсионными характеристиками прямоугольной
ЦСР без плазменного заполнения.
(а) (б)
Рис. 5.1. Дисперсионные
характеристики (а) и характеристическое сопротивление (б) замедляющей системы
с высотой щели связи 1.3 мм при концентрации плазмы ![]() ( 1 ) и
( 1 ) и ![]() ( 2
).
( 2
).
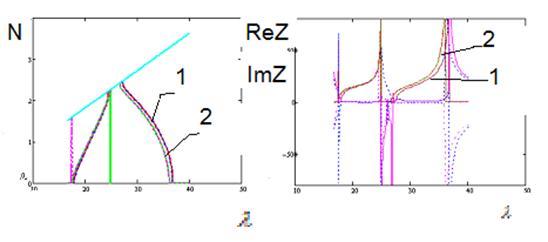
(а)
(б)
Рис. 5.2
Дисперсионные характеристики (а) и характеристическое сопротивление (б) замедляющей
системы с высотой щели связи 4.3 мм при концентрации плазмы ![]() ( 1 ) и
( 1 ) и ![]() ( 2
).
( 2
).
Из рисунков видно, что при увеличении концентрации плазмы дисперсионная характеристика смещается в область более высоких частот. В том случае, когда высота щели связи (4.3 мм) больше толщины резонатора, происходит параллельное смещение дисперсионной характеристики. Если высота щели связи (1.3 мм) меньше толщины резонатора, происходит смещение только длинноволнового края дисперсионной характеристики. Увеличение концентрации плазмы в первом случае приводит к сужению полосы и, соответственно, росту характеристического сопротивления. Во втором случае ширина полосы при смещении сохраняется, но в выбранной полосе частот характеристическое сопротивление все равно увеличивается.
При подборе определенной геометрии прямоугольной ЗС, радиуса пролетного канала и концентрации плазмы можно добиться слияния полос и расширения рабочей полосы ЗС в область высоких частот (рис.5.3, 5.4).
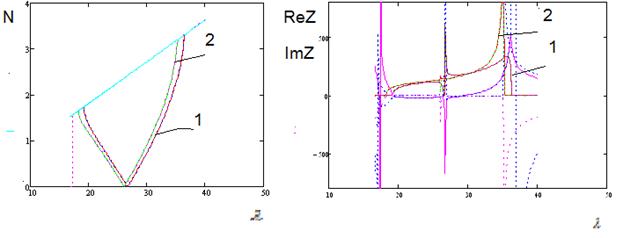
(а) (б)
Рис.5.3. Дисперсионные характеристики
(а) и характеристическое сопротивление (б) прямоугольной ЗС при концентрации
плазмы ![]() ( 1 ) и
( 1 ) и ![]() (
2 ) .
(
2 ) .
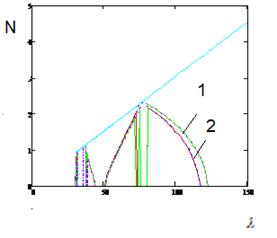
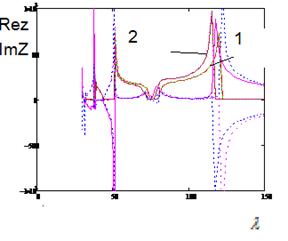
(а) (б)
Рис.5.4.
Дисперсионные характеристики (а) и характеристическое сопротивление (б) аксиально-симметричной
ЗС при концентрации плазмы ![]() ( 1 ) и
( 1 ) и ![]() ( 2 ).
( 2 ).
6. Выводы.
В ходе данной работы были рассмотрены способы представления ячейки резонаторной замедляющей системы многополюсником, а также рассмотрены методы определения элементов матричного оператора 2N-полюсника, описывающего характеристики замедляющих систем. Дан обзор численных методов расчета, а также сделан краткий обзор программ, реализующих численные методы.
В результате проделанной работы был получен алгоритм и программы расчета дисперсионных характеристик резонаторных замедляющих систем с использованием результатов их трехмерного моделирования.
Был выполнен расчет двух замедляющих систем, имеющих прямоугольное и круглое поперечные сечения. При расчете использовались различные методы рассечения ячейки замедляющей системы, в частности, по щели связи и по пролетному каналу.
Расчет производился для двух вариантов трехмерных моделей: без учета пролетного канала, что соответствует четырехполюснику, и с учетом пролетного канала, что соответствует восьмиполюснику. Для замедляющей системы без учета пролетного канала выявлено наличие мнимой части характеристического сопротивления вблизи границ полосы пропускания.
Выполнено моделирование плазмы и проведено исследование дисперсионных характеристик моделей с плазменным заполнением пролетного канала. Анализ дисперсионных характеристик гибридных замедляющих систем подтвердил адекватность полученных результатов известным экспериментальным данным и показал, что характеристическое сопротивление при введении в канал плазмы увеличивается, а при определенном подборе геометрии ЗС и концентрации плазмы возможно слияние полос и расширение рабочей полосы в область высоких частот.
1. Никольский В.В. Вариационные методы для задач дифракции. //Известия Вузов. Радиофизика, 1977, т.20, №1, с.5.
2. Никольский В.В., Никольская Т.И. Декомпозиционный подход к задачам электродинамики. М., Наука, 1983, с. 304.
3. Wathins D.A. Topics in Electromagnetic Theory. №4, 1958.
4. Краснушкин П.Е. Нориальные волны в цепочке многополюсных фильтров. //Журнал технической физики, 1947, т.17, №6, с.705.
5. Ткач Ю.В., Файнберг Я.Б., Гадецкий Н.П. и др. Укр. Физ. Журн., 1978, т. 23, с.1902.
6. Файнберг Я.Б., Блиох Ю.П., Корнилов Е.А. и др. Докл. АН УССР, Физ.-мат. и тех. Науки, 1990, №11, с.55.

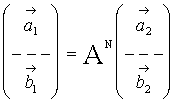
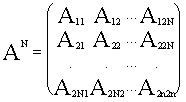 .
(2.4)
.
(2.4)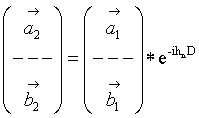
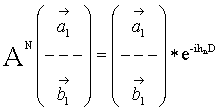 .
.