УДК 001.891.573
ЧИСЛЕНОЕ МОДЕЛИРОВАНИЕ И ОПТИМИЗАЦИЯ ПОГЛОЩАЮЩИХ СВОЙСТВ НЕКОТОРЫХ РАДИОПОГЛОЩАЮЩИХ МАТЕРИАЛОВ
А. В. Никитенко 1,2, А. С. Зубов 2, А. Н. Боголюбов 1
1 МГУ имени М.В. Ломоносова, физический факультет
2 ИТПЭ РАН
Статья получена 20 апреля 2015 г.
Аннотация. В работе рассматривается численное моделирование радиопоглощающих материалов, использующихся в современных безэховых камерах. Предложен способ оптимизации свойств радиопоглощающего материала при нормальном падении, а именно, понижение уровня отражения дифракционных лепестков. Основная идея оптимизации состоит в покрытии материала одним или несколькими согласующими слоями. Рассмотрены наиболее часто встречающиеся материалы клиновидной и пирамидальной формы. Численные эксперименты выполнены с помощью программы, основанной на методе связанных волн. С помощью численного эксперимента найдена зависимость толщины согласующего слоя от частоты, на которой наблюдается оптимальное согласование. Так же рассмотрены материалы с двойным согласующим покрытием. Представлены расчеты зависимости отраженных амплитуд от частоты падающего поля.
Ключевые слова: метод связанных волн, радиопоглощающий материал, безэховая камера.
Abstract. Numerical modeling of radio-absorbing materials commonly used in anechoic chambers is presented in this work. The method of optimization of radio-absorbing properties of such materials in case of normal incidence is suggested. Better properties are obtained by lowering reflection levels of diffraction orders. The main idea of optimization is to coat material with one or more matching layers. Pyramidal and wedge shaped materials are considered. RCWA-algorithm based program was used for numerical experiments. The relation between layer width and best-matching frequency is experimentally obtained. Materials with double coating are also considered. Reflection characteristics in relation to frequency are presented.
Key words: RCWA, radio-absorbing materials, anechoic chamber.
Введение
Безэховые камеры широко используются для измерения электромагнитных характеристик различных объектов и для проведения тестов по электромагнитной совместимости [1]. Эти камеры представляют собой помещение, стены которого покрыты радиопоглощающим материалом. Волны, падающие на этот материал, практически не отражаются, что позволяет с определенным уровнем точности считать измерения в камере эквивалентными измерениям на открытой местности. Однако на практике материалы не могут быть идеально поглощающими на всех углах падения и во всем диапазоне частот, на которых проводятся измерения в камере. Поэтому актуальной является задача численного моделирования отражающих свойств радиопоглощающих материалов, использующихся в современных безэховых камерах и с целью дальнейшего использования результатов моделирования для оптимизации характеристик материалов. Наибольшее распространение в таких камерах получили однопериодические материалы клиновидной формы, и двух периодические материалы пирамидальной формы. Спецификации фирм – производителей РПМ обычно описывают частотно-угловые зависимости лишь для зеркального отражения. В то время как диапазон длин волн в безэховой камере чаще всего включает длины волн, сравнимые с характерными размерами материала (например, периодом), или даже меньше. В случае облучения материала на таких частотах уровень побочных гармоник становится сравним или даже выше уровня зеркального отражения, то есть рассеяние в направлении дифракционных лепестков вносит существенный вклад в полную энергию, отраженную материалом. Полный учет отражения во всех направлениях позволяет более точно оценить эффективность конкретного материала и сформулировать требования к РПМ при создании новой камеры или усовершенствовании старой. Поэтому вопрос выбора оптимальных материалов и конфигурации камер представляет собой важную задачу численного моделирования. В данной работе рассматривается наиболее типичный случай нормального падения волны на одну из стенок камеры что соответствует ситуации со стенкой БЭК, расположенной напротив облучающей системы. Для обоих типов материалов предложено улучшение путем покрытия дополнительным слоем из т.н. “согласующего” материала. На основе численных расчетов клиновидного материала проведена оценка зависимости оптимальной толщины согласующего слоя от частоты, на которой требуется максимальное поглощение полной отраженной энергии. Так же предложено покрытие из двух “согласующих” слоев для обоих типов материалов. Представлены результаты численного моделирования всех рассмотренных материалов, а именно, зависимости амплитуд отраженных волн от частоты падающей волны. Полученные результаты показали высокую эффективность согласующего покрытия.
Постановка задачи
На рис. 1а,б представлены зависимости от частоты величины зеркального отражения плоской волны, падающей нормально или под небольшим углом к нормали к поверхности типичного клиновидного и пирамидального радиопоглощающих материалов. На этих же рисунках показаны аналогичные зависимости для побочных гармоник. Видно, что в большом диапазоне частот амплитуда отраженных гармоник значительно превосходит зеркальное отражение. Такое отражение должно оказывать значительное влияние на поле в рабочей зоне. Поскольку побочные гармоники распространяются под углами от материала, то можно расположить рабочую зону таким образом, чтобы в нее не попадали отраженные гармоники. Однако, подобное решение не всегда осуществимо, так как размеры камеры могут быть ограничены по размеру и стоимости.
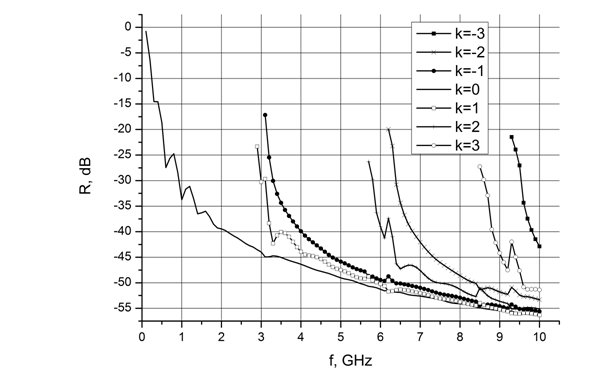
Рис. 1а. Зависимость амплитуды зеркального отражения (сплошная линия) и отраженных гармоник от частоты падающего поля. Клиновидный радиопоглощающий материал. Углы падения: φ=80°, θ=10°.

Рис. 1б. Зависимость амплитуды зеркального отражения (сплошная линия) и отраженных гармоник от частоты падающего поля. Пирамидальный радиопоглощающий материал. Углы падения: φ=0°, θ=0°.
В данной работе проведено численное моделирование радиопоглощающих материалов с согласующими покрытиями. Использование таких модифицированных РПМ должно понизить амплитуду отраженных побочных гармоник.
Численные эксперименты были выполнены с помощью специальной программы расчета коэффициентов отражения от периодических структур, написанной авторами на языке С++ с использованием библиотек Intel Math Kernel Library. Программа реализует алгоритм расчета, основанный на методе связанных волн (Rigorous Coupled Wave Analysis), который входит в семейство Фурье-методов (Fourier Modal Method) [2-5]. Этот метод позволяет получать гармоники отдельно, а так же он был модифицирован для улучшения сходимости и численной стабильности расчетов. Подробное описание использованного алгоритма можно найти в работах [6, 7]. Перед непосредственным проведением экспериментов алгоритм прошел сравнение результатов расчета на модифицированном материале с программой HFSS, основанной на методе конечных элементов.

Рис. 2. График зависимости действительной и мнимой части диэлектрической проницаемости радиопоглощающего материала, использовавшегося в расчетах, от частоты.
Численное исследование проводилось на основе типичного клиновидного и пирамидального радиопоглощающих материалов. Зависимость диэлектрической проницаемости от частоты для исследуемых материалов представлена на рис. 2. Магнитная проницаемость полагается не зависящей от частоты и равной 1. Размеры исследуемого клиновидного материала: высота клина (без подложки) – 27,8 см, период – 10,2 см, толщина подложки – 2,7 см. Для расчета пирамидального материала были использованы следующие размеры: высота пирамид 27,8 см, период по обеим осям – 10,2 см, толщина подложки – 2,7 см.
Для большей наглядности будем оперировать понятием полного коэффициента отражения, или, полной отраженной энергии, который определяется следующим образом:
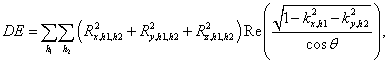
где учтено, что над материалом
расположен воздух, а коэффициенты ![]() ,
, ![]() определяются следующим образом:
определяются следующим образом:
![]()
![]()
где ![]() ,
, ![]() – номер гармоники,
– номер гармоники, ![]() – длина волны падающего поля,
– длина волны падающего поля, ![]() – период материала,
– период материала, ![]() ,
, ![]() - углы падения в сферической
системе координат.
- углы падения в сферической
системе координат.
На рис. 3а представлены графики зависимости коэффициента отражения в зеркальном направлении и полной отраженной энергии от частоты для клиновидного материала. На рис. 3б представлена аналогичная зависимость для пирамидального материала. Обе зависимости рассчитаны при нормальном угле падения и ТЕ-поляризации падающей плоской волны.
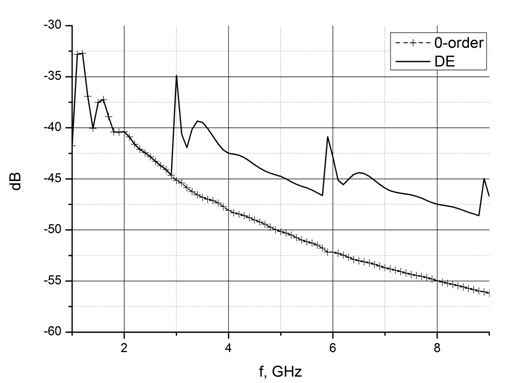
Рис. 3а. Клиновидный материал без модификаций. Полная отраженная энергия (DE), и амплитуда зеркального отражения в зависимости от частоты.
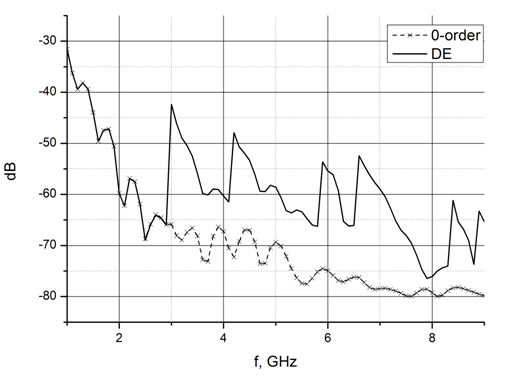
Рис. 3б. Пирамидальный материал без модификаций. Полная отраженная энергия (DE), и амплитуда зеркального отражения в зависимости от частоты.
В данной работе рассматривается возможность уменьшения уровня полной отраженной энергии с помощью модификации материала. Основная идея модификации материала состоит в том, чтобы покрыть его поверхность тонким слоем другого материала с определенной диэлектрической проницаемостью, т.н. согласующим слоем. Такое покрытие должно уменьшить непосредственно уровень отражения от плоской границы раздела “воздух - материал”, т.е. отражение без учета самой геометрической формы материала. Соответственно, использование такого покрытия позволяет понизить уровень отражения в направлении дифракционных лепестков. На рис. 4 представлены клиновидный, пирамидальный материалы, а так же принципиальная схема модификации материала.
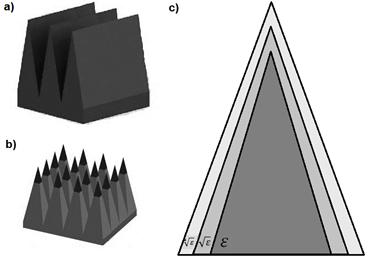
Рис. 4. a) Клиновидный РПМ, b) Пирамидальный РПМ, c) Схема устройства двухслойного согласующего покрытия.
Результаты численных экспериментов
Для определения оптимальных параметров модифицированного материала была рассмотрена более простая задача отражения от однопериодического материала клиновидной формы. Для этого материала была посчитана серия кривых – зависимостей полной отраженной энергии от частоты при различных значениях параметра – толщины согласующего слоя. Диэлектрическая проницаемость покрытия полагалась равной квадратному корню из диэлектрической проницаемости материала, что уравнивает коэффициенты отражения от обеих границ раздела и дает глубокий минимум для суммарной амплитуды при противофазном сложении сигналов, отраженных от границ раздела между слоями с разной диэлектрической проницаемостью. Для выбора оптимальной толщины материала была построена зависимость длины волны, соответствующей частоте минимума, от оптической длины пути волны в согласующем слое (Рис. 5).
По этому графику были найдены первые приближения толщин слоев для оптимизации клиновидного и двухпериодического пирамидального материала на заданном диапазоне частот. Так же была построена аналогичная серия кривых для покрытия из двух слоев – диэлектрическая проницаемость внутреннего слоя такая же, как у однослойного покрытия, а проницаемость внешнего слоя – квадратный корень из проницаемости внутреннего слоя.
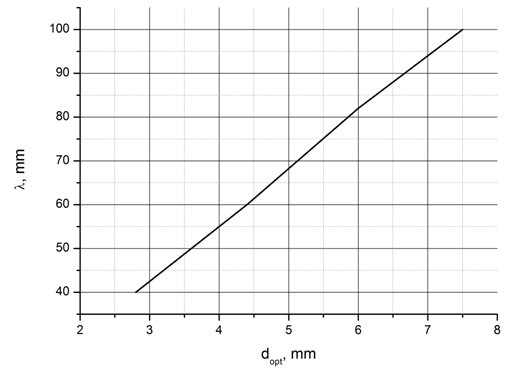
Рис. 5. Зависимость длины волны, соответствующей оптимальной рабочей частоте покрытия от оптической длины пути в согласующем слое.
На Рис. 6а, б представлен сравнительный расчет для клиновидного материала с одно- и двухслойным покрытиями. На приведенном графике видно, что уровень полной отраженной энергии в среднем понизился на 10 дБ в диапазоне частот 2.5-3.5 ГГц, толщина согласующего слоя составила порядка 5 мм.
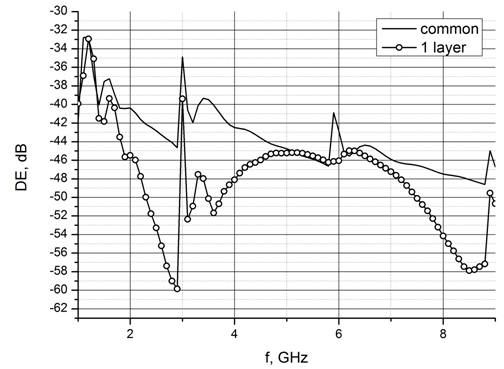
Рис. 6а. Сравнение зависимости полной отраженной энергии от частоты для обычного клиновидного материала (common) и клиновидного материала с одним согласующим слоем (1-layer).

Рис. 6б. Сравнение зависимости полной отраженной
энергии от частоты для обычного клиновидного материала (common) и клиновидного материала с двумя согласующими слоями (2-layers).
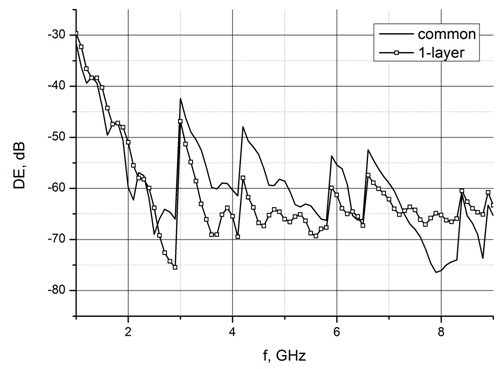
Рис.7а Сравнение зависимости полной отраженной энергии от частоты для обычного пирамидального материала (common) и клиновидного материала с одним согласующим слоем (1-layer).
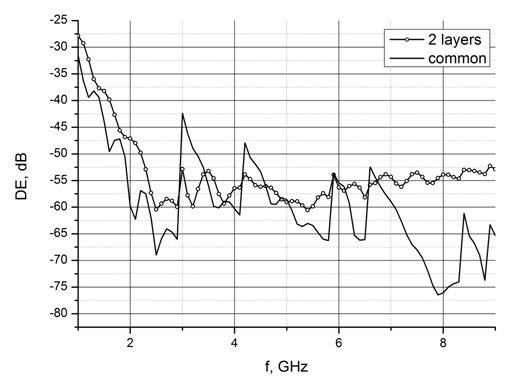
Рис.7б Сравнение зависимости полной отраженной энергии от частоты для обычного пирамидального материала (common) и клиновидного материала с двумя согласующими слоями (2-layers).
Полученные толщины согласующих слоев были использованы в качестве первого приближения для оптимизации пирамидального РПМ. На рис. 7а, б приведены результаты расчета полной отраженной энергии от пирамидального РПМ в зависимости от частоты, с однослойным покрытием и с двухслойным. Видно, что удалось добиться понижения уровня отраженной энергии на 10 дБ в диапазоне 3.5-5 ГГц. Толщина внутреннего слоя составила порядка 5 мм, внешнего – 6 мм.
Заключение
В работе приведены расчеты влияния незеркального отражения (дифракционных лепестков) на общую отраженную от РПМ энергию. Показано, что на многих частотах вклад дифракционных лепестков сильно превышает вклад зеркального отражения, особенно сильно этот эффект проявляется при нормальном падении волны, то есть в условиях, при которых РПМ должен работать максимально эффективно. Предложен способ понижения полной отраженной от РПМ энергии на диапазоне частот при помощи покрытия материала тонкими согласующими слоями. Представлены результаты численного эксперимента, позволяющего оценить необходимую толщину слоев в зависимости от частоты, на которой требуется максимальное поглощение. На основе этих данных проведены расчеты коммерческого клиновидного и пирамидального материалов, получивших наибольшее распространение в безэховых камерах. Представлено сравнение полной отраженной энергии без согласующего слоя, с одним и двумя согласующими слоями для обоих видов материалов. Подавление побочных гармоник составило более 10 дБ в заданном диапазоне частот, что можно считать достаточно хорошим результатом, который может быть использован для создания новых материалов с покрытиями. Также планируется дальнейшее исследование материалов с согласующими покрытиями с более широким диапазоном частот, на котором покрытие действует наиболее эффективно.
Литература
1. Балабуха Н.П., Зубов А.С., Солосин В.С. Компактные полигоны для измерения характеристик рассеяния. М.:Наука, 2007.
2. D. Maystre. M. Neviere. Electromagnetic theory of crossed gratings // J. Optics (Paris), 1978, vol. 9, no 5, pp. 301-306
3. E. Noponen, J. Turunen. Eigenmode method for electromagnetic synthesis of diffractive elements with three-dimensional profiles. // J. Opt. Soc. Am. A/Vol. 11, No. 9/September 1994
4. Moraham M.G., Grann E.B., Pommet D.A., Gaylord T.K.. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings. // J. Opt. Soc. Am. A 12, 1068-1076 (1995).
5. J.P. Hugonin, P.Lalanne, I. Delvillar, I.R. Matias. Fourier modal methods for modeling optical dielectric waveguides // Optical and Quantum Electronics (2005) 37:107–119
6. А.В. Никитенко, А.С. Зубов, Н.Е. Шапкина. Моделирование электромагнитного рассеяния на радиопоглощающем материале методом связанных волн. // Математическое моделирование, 2014, том 26, номер 9, стр. 18-32.
7. А.В. Никитенко, А.С. Зубов, Е.В. Булычев. 3D моделирование электромагнитного рассеяния на РМП методом связанных волн. // Журнал Радиоэлектроники (электронный журнал), 2014 . №12. URL: